Self-Quiz Unit 5
Question1 What property does the Fibonacci Sequence have?
Not answered
Marked out of Select one:
1.00 O a. It doubles in value every 5 numbers and then becomes infinite rather quickly.
O b. At som
...
Self-Quiz Unit 5
Question1 What property does the Fibonacci Sequence have?
Not answered
Marked out of Select one:
1.00 O a. It doubles in value every 5 numbers and then becomes infinite rather quickly.
O b. At some point, it becomes 0 and then stops.
O c. It adds the two previous numbers of a sequence together and continues
forever.
O d. It is undecided if the Fibonacci Sequence stops or not.
O e. It multiplies the two previous values of a sequence with each other and
continues forever.
Your answer is incorrect.
The correct answer is: It adds the two previous numbers of a sequence
together, and continues forever.
https://my.uopeople.edu/mod/quiz/review.php?attempt=1567064 1/620/12/20ia
Question 2
Incorrect
Mark 0.00 out of
1.00
Self-Quiz Unit 5
Let On = 2On- 1with starting values of a# = 1 . What is the solution to this
recurrence relation?
Select one:
O a. It has no solution.
b-o„ = ( 2;i. - l )2
c' On = 2’" 1
• d. a* = 2" X
e-(ln = ))“
Your answer is incorrect.
The correct answer is: an = 2"-1
Question 3
Not answered
Marked out of
1.00
Let Fq = = — 2 and£]t = Fk_2 + for JFC > 2. Which one of the
following is the value of F$
Select one:
o a. 14
o b. 13
o c. 46
o d. -46
o e. 12
Your answer is incorrect.
The correct answer is: 14Question 4
Incorrect
Mark 0.00 out of
1.00
Let DK — 2dk-i 4- 3fc- with the starting value a\ = 5. What is the solution
of this recurrence relation?
Select one:
O a. It has no solution.
b. AK = +
C- ak = 3*'+i + 2k+L
• d. ak = 2(ft - l) + 3fcX
e. ak = 2 (ft - 1) + 3k
Your answer is incorrect.
The correct answer is: ak = 3*"1"1 4- 2fc+1
Question 5
Correct
Mark 1.00 out of
1.00
Consider the formula Ll ) 4- 1). What is the result?
Select one:
b-( L " ) - i
c. n
O /
e .ft
Your answer is correct.
The correct answer is:Mark 0.00 out of
1.00
Question 6
Incorrect
Let On = (in- 1 + n with a starting value of g.q = 4. What is the solution to
this recurrence relation?
Select one:
O a. It has no solution.
b.(h, = i +
c-o„ = 2 + ^ ± ^
2
0-an = i + fe-an = 4 4- n X
Your answer is incorrect.
The correct answer is: = 4 4-
Question 7
Correct
Mark 1.00 out of
1.00
Let (in = 4an-\_ — 4an- 2 with starting values of ci0 = 1 and q,\ = 2. What
is the solution to this recurrence relation?
Select one:
O a. It has no solution.
b-^ = {A n - l )2
c-On = An2
d an = n4
e. a*n = T V
Your answer is correct.
The correct answer is: an = 2nQuestion 8 If a recurrence relation S(k) has the characteristic equation
Correct x2 -\- 2x — 8 = (z — 2)(x -\- 4), then which one of the following is the
Mark 1.00 out of general solution.
1.00
Select one:
a. a2k + fr( —4)^ /
b. a(-2 )* + &4fc
c-2fc-4fc
d-a2k - b8k
e-2ak - 4bk
Your answer is correct.
The correct answer is: a2k + &( — 4 )fc
Question 9
Incorrect
Mark 0.00 out of
1.00
Let ]In = 2//n_ i + 1 with rc > 1 and Hq = 0. What is the solution to this
recursive equation?
Select one:
a. IIn = 2" - 1
b //n = 2fc
c-Hn = 2° + l
d. Hn — n2 + ftYour answer is incorrect.
The correct answer is: Hn = 2" — 1Mark 0.00 out of
1.00
Question 10
Incorrect
Which of the following is a closed-form expression for the solution of the
recurrence B (0) = 1 , B(k) = B(k —1) + 4, k > 1?
Select one:
• a-B W = E ^ ( f l ( « ) + 4 ) X
b. B(k) = + 1
c. B(k) = 2k + 1
d B(k) = 4* + 1
e-B(k) = 2 k
Your answer is incorrect.
The correct answer is: B(k) = 4k + 1MATH 1302 Discrete Mathematics - Term 2, 2018-2019
Home ► My courses ► MATH 1302 - AY2019-T2 ► 13 December - 19 December ►
Self-Quiz Unit 5
Started on
State
Completed on
Time taken
Grade
Sunday, 16 December 2018, 4:44 PM
Finished
Sunday, 16 December 2018, 5:48 PM
1 hour 3 mins
4.00 out of 10.00 (40%)
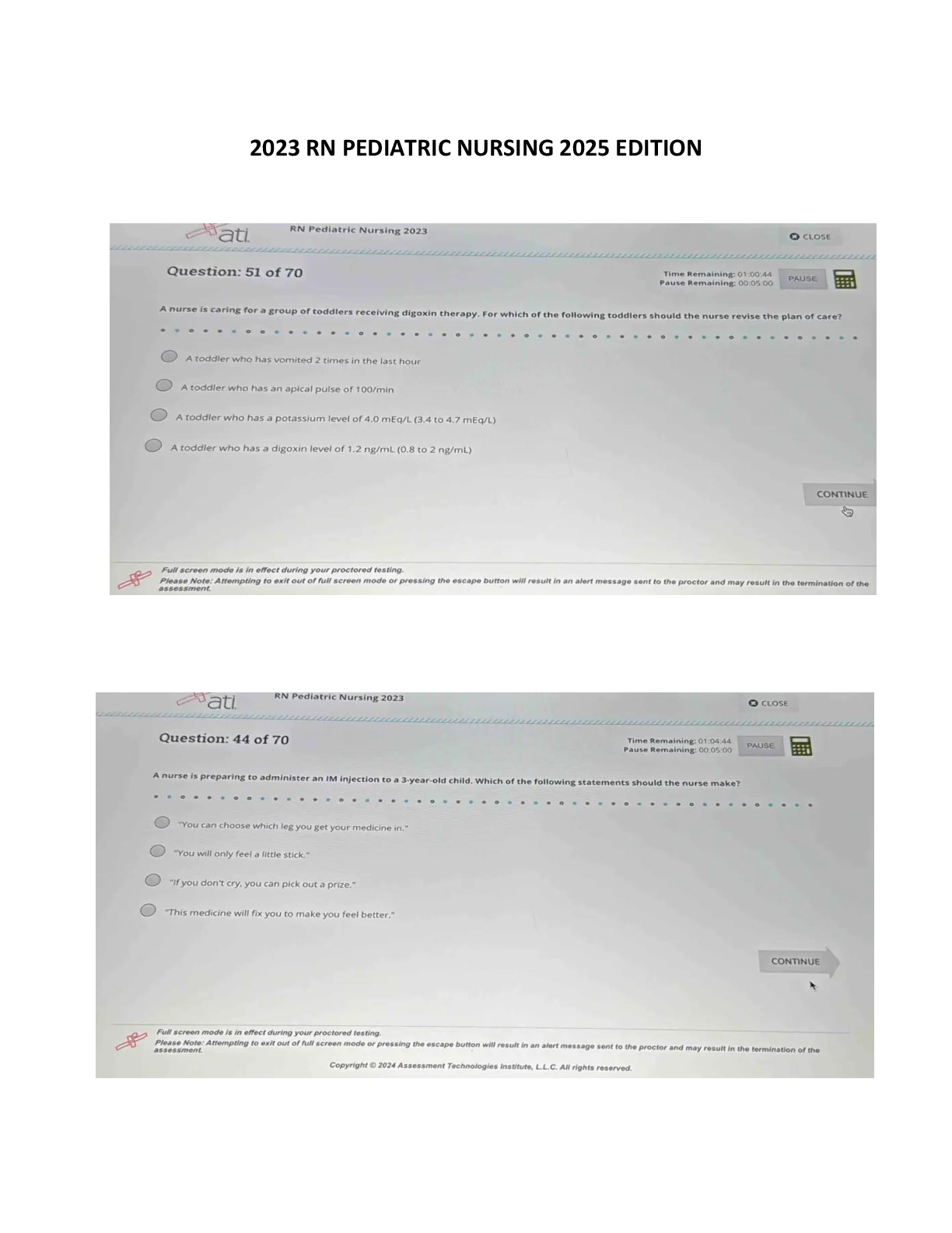
Question 1 Let i?(0 ) = 0, # ( l ) = 1 and R(k) = 2R(k — 1) + R(k — 2) — 1for all
incorrect k > 2. Which one of the following is the correct value of RiJj 'j?
Mark 0.00 out of
1.00 Select one:
O a. 5
O b. 9
• c. 4 X
O d. 21
O e. 1
Your answer is incorrect.
The correct answer is: 9Mark 1.00 out of
1.00
Question 2
Correct
Your answer is correct.
The correct answer is: 13
Question 3 Which one of the following is the characteristic polynomial of the
Correct recurrence relation S(k) = 3S(k — 1 ) + 6S(k —2 ) — SS(k —3)?
Mark 1.00 out of
1.00 Select one:
a-XS + 3;t'2 + 6x —8
b- 3x2 -f Qx - 8
c-x 3 —3a;2 — 6a; 4- 8 V
d. x4 - 3x3 + 6.T- - 8.t
e-;r4 + - 6z 2 -f 82:
Your answer is correct.
The correct answer is: _ 3^ _ 6a; + 8Question4 Let T(0) = Oand Tin) = 1 4- T{\_nj2\ ) for n > 0. Which one of the
Incorrect following is a solution for T(n) when n = 2WMark 0.00 out of
1.00 Select one:
a. T(2m) = m 4- 1
b. T(2m) = m
c. T(2m) = m — 1
d. T{2m) = 2m
e. T(2m) = 2mX
Your answer is incorrect.
The correct answer is: T(2m) = m 4- 1
Question5
Incorrect
Mark 0.00 out of
1.00
If a recurrence relation S(k) has the characteristic equation
■ ■- 1,. ■ 1 .' 1- then which one of the following is the correct
form of the general solution of S(k'f?
Select one:
a- a3k + b3k
b. a (-6 )k + b9k
c. {a -f bk)(—3)kX
d- a3k
e (a -I- 6A’)3fc
Your answer is incorrect.
The correct answer is: (a -f bk)3kMark 0.00 out of
1.00
Question 6
Incorrect
Question 7
Incorrect
Mark 0.00 out of
1.00
What does "Recursion" mean?
Select one:
• a. Defining something recursive means it is infinite. X
O b. The application of a function/definition to its own values.
O c. Defining a function or set in such a way that it has finite and well defined
values/elements.
O d. Recursive functions usually produce an error, for example a division by zero.
O e. Recursion means the result is always one.
Your answer is incorrect.
The correct answer is: The application of a function/definition to its own
values.
Which one of the following is a solution of the recurrence relation
S(k) = 3S(k - 1) + 4 with 5 (1 ) = 1?
Select one:
a-S(k) = 5* — 4
b.S(k) = 6* - 5
c. S(k) = 2 k - 1
d.S{k) = k X
e. S(k) =3* -2
Your answer is incorrect.
The correct answer is: S(k) = 3* — 2Mark 0.00 out of
1.00
Question 8
Incorrect
Question 9
Correct
Mark 1.00 out of
1.00
Consider the sequence: 1,1,2,3,5,8,13,21,34,55,...
What is the recurrence relation for this sequence?
Select one:
a- = &n—l + 2&n—2X
k- (In = 2 + dn—2
c-&n — d„ —1 + dn—2
O d. It is a random sequence that has no recurrence relation.
e-ftn = <4- 1
Your answer is incorrect.
The correct answer is: a „ = a^ -i + &n-i
What methods can you use to solve recurrence relations?
Select one:
O a. Solving Differential Equations.
O b. Simplifying Binomials.
• c. Iteration, Telescoping or finding Characteristic Roots. V
O d. Multiplication and Division.
O e. Logical Elimination.
Your answer is correct.
The correct answer is: Iteration, Telescoping or finding Characteristic Roots.Mark 1.00 out of
1.00
Question 10
Correct
Let dk — 2dk-i + 3fc- with the starting value a\ = 5. What is the solution
of this recurrence relation?
Select one:
O a. It has no solution.
b. ak = +
• c. ak - 3*+1 4- 2k+l /
d. ak = 2(k - 1) + 3fc
e. ak = 2 (k - 1) + 3k
Your answer is correct.
The correct answer is: ak = 3*"1"1 4- 2fc+1
https://my.uopeople.edu/mod/quiz/review.php?attempt=1567684 6/6MATH 1302 Discrete Mathematics - Term 2, 2018-2019
Home ► My courses ► MATH 1302 - AY2019-T2 ► 13 December - 19 December ►
Self-Quiz Unit 5
Started on
State
Completed on
Time taken
Grade
Sunday, 16 December 2018, 6:00 PM
Finished
Sunday, 16 December 2018, 6:06 PM
5 mins 43 secs
10.00 out of 10.00 (100%)
Question 1 Consider the sequence: 1,1,2,3,5,8,13,21,34,55,...
Correct What is the recurrence relation for this sequence?
Mark 1.00 out of
1.00 Select one:
a-&n — &n—1 + 2fln—2
k- (In — 2 0 n _l + f l „ - 2
c-&n = &n—1 “1“ &n— 2
O d. It is a random sequence that has no recurrence relation.
e-^ = al_ i
Your answer is correct.
The correct answer is: an = + On-2Question2 Which one of the following is a solution of the recurrence relation
Correct S(k) = 3S(k — 1 ) + 4 with 5 (1 ) = 1?
Mark 1.00 out of
1.00 Select one:
a.S(k) = 5* — 4
b. S(k) = S k - 5
c.S(k) = 2 k - 1
O
Q_
??
II
e-S(k) = 3 k - 2 s/
Your answer is correct.
The correct answer is: S(k) = 3k — 2
Question 3
Correct
Mark 1.00 out of
1.00
Let On = — 4an_2 with starting values of ao = 1 and a\ = 2. What
is the solution to this recurrence relation?
Select one:
O a. It has no solution.
b. an = (An — l )2
c- an — An2
d On = n4
e.an = 2fl
Your answer is correct.
The correct answer is: an = 2nMark 1.00 out of
1.00
Question 4
Correct
What methods can you use to solve recurrence relations?
Select one:
O a. Solving Differential Equations.
O b. Simplifying Binomials.
• c. Iteration, Telescoping or finding Characteristic Roots. V
O d. Multiplication and Division.
O e. Logical Elimination.
Your answer is correct.
The correct answer is: Iteration, Telescoping or finding Characteristic Roots.
Question5 Let p(x) = ( ( ( r + 2)x — 1 )t ‘ + 3);t' -f 8. What is the value of p{ 1)?
Correct
Mark 1.00 out of Select one:
1.00 O a. 11
O b. -11
O c. 12
• d. 13
O e. -13
Your answer is correct.
The correct answer is: 13Mark 1.00 out of
1.00
Question 6
Correct
Question 7
Correct
Mark 1.00 out of
1.00
Your answer is correct.
The correct answer is: 9
Let On = dn-i + ti with a starting value of Oq = 4. What is the solution to
this recurrence relation?
Select one:
O a. It has no solution.
• b.
O c.
O d.
O e.
Your answer is correct.
The correct answer is: n■fi — 4 4. 9Question8 Which one of the following is the characteristic polynomial of the
Correct recurrence relation S(k) = 3S(k — 1) + GS(k —2) — SS(k —3)?
Mark 1.00 out of
1.00 Select one:
a- + 3a:2 + Go; — 8
b- 3a:2 -f Go' — 8
c-x :i — 3 r 2 — G r + 8 V
d. -r4 - 3 r 1 + Gx2 - 8.t
e-;r4 + 3a’3 - Go-2 + Sx
Your answer is correct.
The correct answer is: - 3 r 2 - 6x + 8
Question 9
Correct
Mark 1.00 out of
1.00
Which of the following is a closed-form expression for the solution of the
recurrence B (0) = 1, B(k) = B(k — 1) + 4, k > 1?
Select one:
a-B W = E l S 3 ( B ( n ) + 4)
b.B{k) = + 1 s/
c. B(k) = 2Jfc + 1
d.B(k) = 4'l’ + 1
e-B(k) = 2k
Your answer is correct.
The correct answer is: B(k) = Ak + 1Question 10
Correct
Let and for A’ > 2. Which one of the
following is the value of F&?
Mark 1.00 out of
1.00 Select one:
• a. 14
O b. 13
O c. 46
O d. -46
O e. 12
Your answer is correct.
The correct answer is: 14
https://my.uopeople.edu/mod/quiz/review.php?attempt=1567748 6/6MATH 1302 Discrete Mathematics - Term 2, 2018-2019
Home ► My courses ► MATH 1302 - AY2019-T2 ► 13 December - 19 December ►
Self-Quiz Unit 5
Started on
State
Completed on
Time taken
Grade
Sunday, 16 December 2018, 6:07 PM
Finished
Sunday, 16 December 2018, 6:11 PM
3 mins 38 secs
10.00 out of 10.00 (100%)
Question 1 Let T ( 0) = 0 and T(n) = 1 -f T ( |_7i / 2j ) for n > 0. Which one of the
Correct following is a solution for T (n ) when n = 2 m -
Mark 1.00 out of
1.00 Select one:
a. T(2m) = m + 1 sj
b. T(2m) = 771
c. T(2m) — 771 — 1
d. T(2m) = 2m
e. T(2m) = 2m
Your answer is correct.
The correct answer is: T(2m) = m -f 1Mark 1.00 out of
1.00
Question 2
Correct
Question 3
Correct
Mark 1.00 out of
1.00
What property does the Fibonacci Sequence have?
Select one:
O a. It doubles in value every 5 numbers and then becomes infinite rather quickly.
O b. At some point it becomes 0 and then stops.
• c. It adds the two previous numbers of a sequence together, and continues
forever. ^
O d. It is undecided if the Fibonacci Sequence stops or not.
O e. It multiplies the two previous values of a sequence with each other, and
continues forever.
Your answer is correct.
The correct answer is: It adds the two previous numbers of a sequence
together, and continues forever.
If a recurrence relation S{k) has the characteristic equation
■ J J ■ i ■ J " . I i, then which one of the following is the
general solution.
Select one:
a. a2k + & (-4 )fc /
b. a(—2")k + b4k
c-2k - 4fc
d-£12* - b8k
e-2ak - 4bk
Your answer is correct.
The correct answer is: a2k + b( —4)*Mark 1.00 out of
1.00
Question 4
Correct
If a recurrence relation S(k) has the characteristic equation
■ J i,. ■ . .■■ then which one of the following is the correct
form of the general solution of Si k)?
Select one:
a- a3k + b3k
b.a (-G )k + bQk
c. (a + bk)(—3)k
d-a3k
e.(a + bk) 3 * V
Your answer is correct.
The correct answer is: (a + bk) 3k
Question 5
Correct
Mark 1.00 out of
1.00
Consider the formula ( f: ^ 1). What is the result?
Select one:
■>■(£ ) - 1
c. n
• d-( ; ' V
e .fe
Your answer is correct.
The correct answer is: (/: )Mark 1.00 out of
1.00
Question 6
Correct
Let IIn = 2 J7 „_i + 1 with n > 1 and J70 = 0. What is the solution to this
recursive equation?
Select one:
a. IIn = 2" - 1 V
b Iln = 2fc
c Hn = 2° + 1
d. / / n = ;j- -1- n
e. //„ = 2" E ! ; = o " 2
Your answer is correct.
The correct answer is: Hn = 2" — 1
Question 7
Correct
Mark 1.00 out of
1.00
What does "Recursion" mean?
Select one:
O a. Defining something recursive means it is infinite.
• b. The application of a function/definition to its own values.
O c. Defining a function or set in such a way that it has finite and well defined
values/elements.
O d. Recursive functions usually produce an error, for example a division by zero.
O e. Recursion means the result is always one.
Your answer is correct.
The correct answer is: The application of a function/definition to its own
values.Mark 1.00 out of
1.00
Question 8
Correct
Let On = 2On- 1with starting values of oq = 1 . What is the solution to this
recurrence relation?
Select one:
O a. It has no solution.
= (2n - 1 )-
• c on = 2n_1/
d. On = T
e- On = n 2
Your answer is correct.
The correct answer is: an = 2"-1
Question 9
Correct
Mark 1.00 out of
1.00
Let Fq = 6, F1 = —2 and Fk = F fc_2 + Fk_ 1for k > 2. Which one of the
following is the value of F^?
Select one:
w a. 14
O b. 13
O c. 46
O d. -46
O e. 12
Your answer is correct.
The correct answer is: 14Question 10
Correct
What methods can you use to solve recurrence relations?
Mark 1.00 out of
1.00
Select one:
O a. Solving Differential Equations.
O b. Simplifying Binomials.
• c. Iteration, Telescoping or finding Characteristic Roots. V
O d. Multiplication and Division.
O e. Logical Elimination.
Your answer is correct.
The correct answer is: Iteration, Telescoping or finding Characteristic Roots.
https://my.uopeople.edu/mod/quiz/review.php?attempt=1567759 6/6MATH 1302 Discrete Mathematics - Term 2, 2018-2019
Home ► My courses ► MATH 1302 - AY2019-T2 ► 13 December - 19 December ►
Self-Quiz Unit 5
Started on
State
Completed on
Time taken
Grade
Sunday, 16 December 2018, 6:12 PM
Finished
Sunday, 16 December 2018, 6:13 PM
1 min 30 secs
10.00 out of 10.00 (100%)
Question 1 If a recurrence relation S(k) has the characteristic equation
Correct x2 -f 2x — 8 = (;f — 2)(x -f 4), then which one of the following is the
Mark 1.00 out of general solution.
1.00
Select one:
a.a2k + & (-4 )fc /
b-a(—2)k + b4k
t-2 k - 4 k
d-a2k - bSk
e-2ak - 4bk
Your answer is correct.
The correct answer is: a2k + b(—4 )fcMark 1.00 out of
1.00
Question 2
Correct
Leti^(O) = 0, /£ (!) = 1 and R(k) = 2R(k — 1) + R(k — 2) — 1for all
k > 2. Which one of the following is the correct value of R(5)?
Select one:
o a. 5
® b. 9
o c. 4
o d. 21
o e. 1
Your answer is correct.
The correct answer is: 9
Question 3
Correct
Mark 1.00 out of
1.00
Which of the following is a closed-form expression for the solution of the
recurrence B (0) = 1 , B(k) = B(k — 1) + 4, k > 1?
Select one:
a-- B W = E ^ ( £ W + 4)
b. B{k) = + 1 s/
c. B(k) = 2Jfc + 1
d. B(k) = 4,L’ + 1
e-B(k) = 2k
Your answer is correct.
The correct answer is: B(k) = Ak + 1Mark 1.00 out of
1.00
Question 4
Correct
Question 5
Correct
Mark 1.00 out of
1.00
What does "Recursion" mean?
Select one:
O a. Defining something recursive means it is infinite.
• b. The application of a function/definition to its own values.
O c. Defining a function or set in such a way that it has finite and well defined
values/elements.
O d. Recursive functions usually produce an error, for example a division by zero.
O e. Recursion means the result is always one.
Your answer is correct.
The correct answer is: The application of a function/definition to its own
values.
Let T (0 ) = 0 and T(n) = 1 -f T{ \_nj2J ) for n > 0. Which one of the
following is a solution for 7 ( j when n = 2m.
Select one:
a. T(2m) = m -fi 1 /
b. T(2m) = m
c. T(2m) — m — 1
d. T(2m) = 2m
e. T(2m) = 2m
Your answer is correct.
The correct answer is: T(2m) = m -f 1Mark 1.00 out of
1.00
Question 6
Correct
Let On = 4dfl_ i — 4an_2 with starting values of r(0 = 1 and a\ = 2. What
is the solution to this recurrence relation?
Select one:
O a. It has no solution.
b-On = (4n - 1)-
c On = Art2
d On = n4
e.a^ = T V
Your answer is correct.
The correct answer is: an = 2n
Question 7
Correct
Mark 1.00 out of
1.00
Consider the formula ( '' 1) + ( . 1). What is the result?
Select one:
■•(£=?)
•>■(£ ) - 1
c. n
e-k
Your answer is correct.
The correct answer is:Mark 1.00 out of
1.00
Question 8
Correct
Your answer is correct.
The correct answer is: 13
Question 9 Which one of the following is the characteristic polynomial of the
Correct recurrence relation S(k) = 3S(k — 1 ) + 6S(k —2 ) — SS(k —3)?
Mark 1.00 out of
1.00 Select one:
a-XS + 3;t'2+ 6x —8
b- 3x2 -f 6x - 8
c-x 3 —3:r2 — 6:r 4- 8 V
d. ;r 4 - 3 x 3 + 6 .T - - 8.t
e-;r4 + 3x 'J - 6.t- + Sx
Your answer is correct.
The correct answer is: _ 3r 2 _ + gMark 1.00 out of
1.00
Question 10
Correct
• c. It adds the two previous numbers of a sequence together, and continues
forever. ^
O d. It is undecided if the Fibonacci Sequence stops or not.
O e. It multiplies the two previous values of a sequence with each other, and
continues forever.
Your answer is correct.
The correct answer is: It adds the two previous numbers of a sequence
together, and continues forever.
What property does the Fibonacci Sequence have?
Select one:
O a. It doubles in value every 5 numbers and then becomes infinite rather quickly.
O b. At some point it becomes 0 and then stops.
https://my.uopeople.edu/mod/quiz/review.php?attempt=1567768 6/6
[Show More]