Pure Mathematics

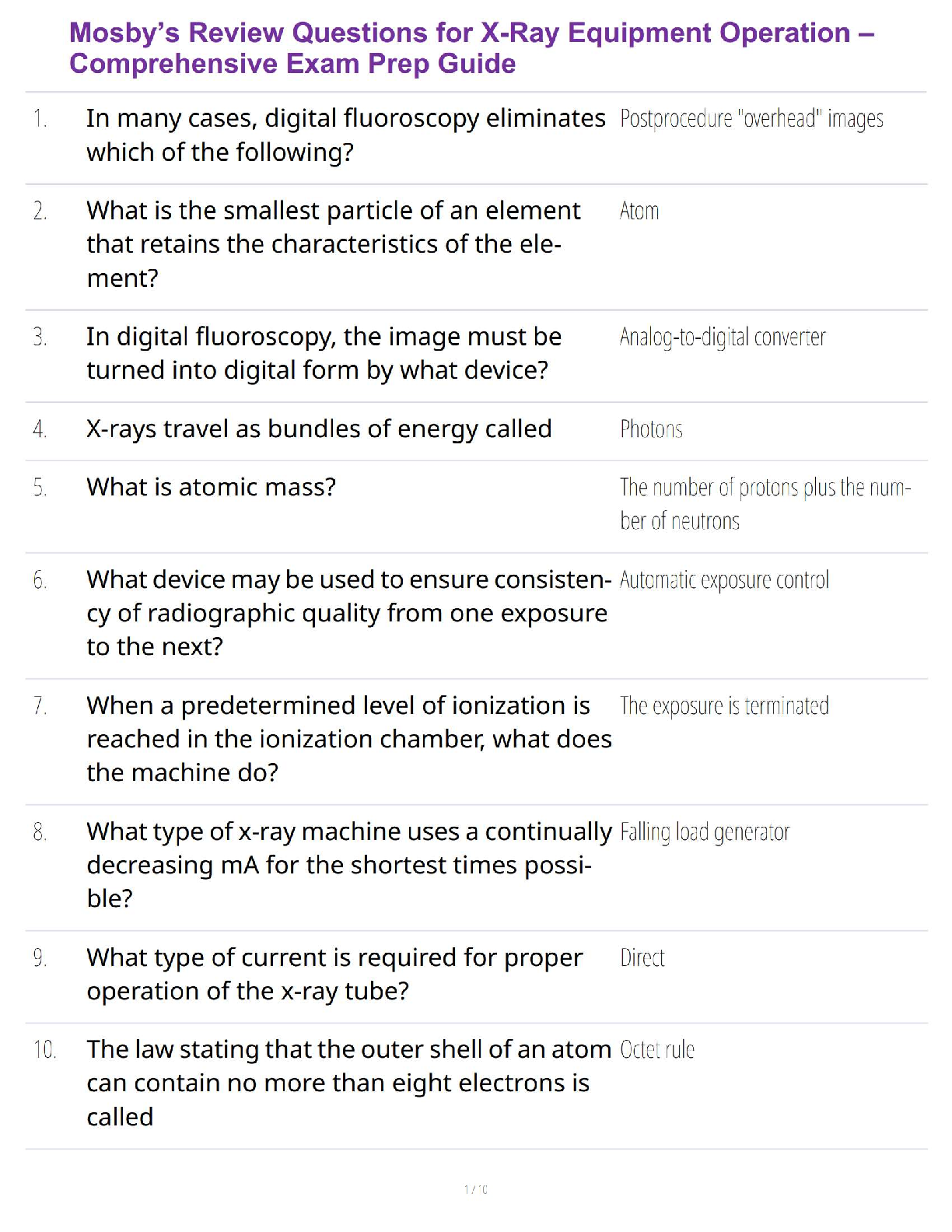
The quadratic equation 3(k + 2)x2 + (k +5)x + k = 0 has real roots. Find the set of possible values of k. (6) ......................................................................................................... ...

The quadratic equation 3(k + 2)x2 + (k +5)x + k = 0 has real roots. Find the set of possible values of k. (6) .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. ................................................................................................................................................................................................................................................... .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. (Total for Question 1 is 6 marks) http://britishstudentroom.wordpress.com/4 *P66024A0436* 2 Angle α is acute such that cos α = 3 5 Angle β is obtuse such that sinβ = 1 2 (a) Find the exact value of (i) tanα (ii) tanβ (3) (b) Hence show that tan(α + β) = m n n m 3 3 − + where m and n are positive integers whose values are to be found. (3) .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. ................................................................................................................................................................................................................................................... .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. http://britishstudentroom.wordpress.com/*P66024A0536* Turn over 5 Question 2 continued .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. .................................................................................................................................................................................................................................................. (Total for Question 2 is 6 marks) http://britishstudentroom.wordpress.com/6 *P66024A0636* 3 A curve C has equation y = ax x −+ 3 5 where a is a constant and x ≠ –5 The gradient of C at the point on the curve where x = 2 is 18 49 (a) Show that a = 3 (3) Hence (b) write down an equation of the asymptote to C that is (i) parallel to the x‑axis, (ii) parallel to the y‑axis, (2) (c) find the coordinates of the point where C crosses (i) the x‑axis, (ii) the y‑axis. (2) (d) Sketch the curve C, showing clearly its asymptotes and the coordinates of the points where C crosses the coordinate axes