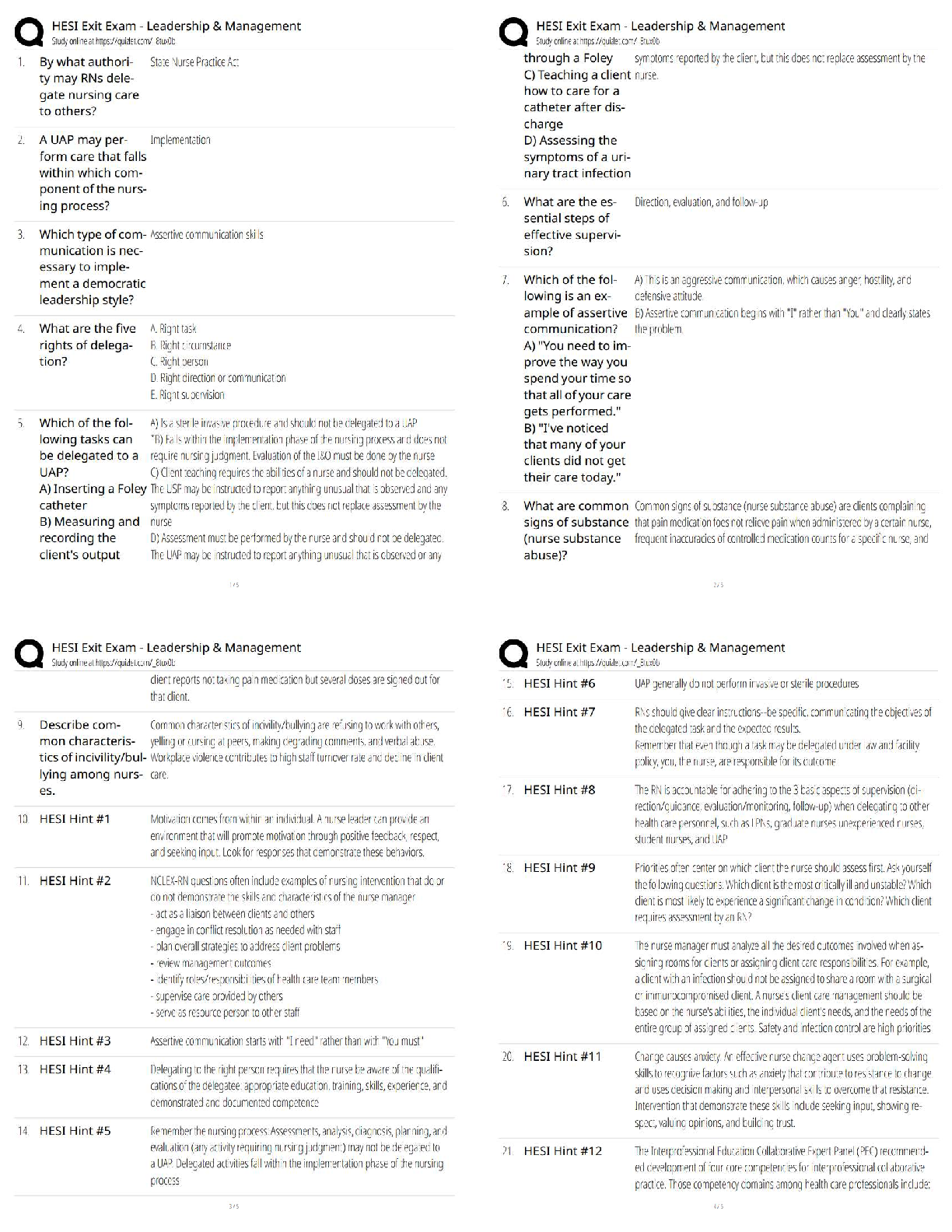
Chapter 7: Business Analytics_ Data Analysis _ Decision Making

Document Content and Description Below

1. The standard error of sample mean is large when the observations in the population are spread out (large ), but that the standard error can be reduced by taking a smaller sample. a. True b. Fals... e 2. A sample in which the sampling units are chosen from the population by means of a random mechanism is a a. probability sample b. judgmental sample c. stratified sample d. systematic sample 3. A judgmental sample is a sample in which the a. sampling units are chosen using a random number table b. quality of sampling units judged c. sampling units are chosen according to the sampler’s judgment d. sampling units are all biased and vocal about it 4. Potential sample members, called sampling units, are: a. people b. companies c. households d. All of these options 5. In sampling, a population is: a. the set of all humans b. the set of all members about which a study intends to make inferences c. any group of test subjects d. a random group of individuals, households, cities or countries 6. A list of all members of the population is called a: a. sampling unit b. probability sample c. frame d. relevant population 7. A list of all members of the population from which we can choose a sample is called a frame, and the potential sample members are called sampling units. a. True b. False Copyright Cengage Learning. Powered by Cognero. Page 1 Name: Class: Date: Chapter 07 8. A probability sample is a sample in which the sampling units are chosen from the population by means of a random mechanism such as a random number table. a. True b. False 9. A sample chosen in such a way that every possible subset of same size has an equal chance of being selected is called a(n) a. interval estimation b. point estimation c. simple random sample. d. statistic 10. The sampling method in which a population is divided into blocks and then selected by choosing a random mechanism is called a a. random sampling b. systematic sampling c. stratified sampling d. cluster sampling 11. Which of the following is not a consideration when determining appropriate sample size? a. The cost of sampling b. The timely collection of the data c. Interviewer fatigue d. The likelihood of nonsampling error 12. Identifiable subpopulations within a population are called: a. clusters b. samples c. blocks d. strata e. None of these options 13. The defining property of a simple random sample is that: a. every sample has the same chance of being chosen b. the easiest method to access samples are chosen c. the fewest samples are chosen d. every fourth subject is chosen as a sample Copyright Cengage Learning. Powered by Cognero. Page 2 Name: Class: Date: Chapter 07 14. Selecting a random sample from each identifiable subgroup within a population is called: a. random sampling b. systematic sampling c. stratified sampling d. cluster sampling e. None of these options 15. Which of the following are reasons for why simple random sampling is used infrequently in real applications? a. Samples can be spread over a large geographic region b. Simple random sampling requires that all sampling units be identified prior to sampling c. Simple random sampling can result in underrepresentation or overrepresentation of certain segments of the population d. All of these options 16. With proportional sample sizes: a. The proportion of a stratum in the sample is independent of the proportion of that stratum in the population b. The proportion of a stratum in the sample is the same as the proportion of that stratum in the population c. The proportion of a stratum in the sample is greater than the proportion of that stratum in the population d. The proportion of a stratum in the sample is less than the proportion of that stratum in the population 17. Simple random samples are typically used in real applications. a. True b. False 18. A simple random sample is one where each member of the population has a known chance (this may differ from one member to another) or probability of being chosen. a. True b. False 19. In systematic sampling, one of the first k members is selected randomly, and then every kth member after this one is selected. The value k is called the sampling interval and equals the ratio N / n, where N is the population size and n is the desired sample size. a. True b. False Copyright Cengage Learning. Powered by Cognero. Page 3 Name: Class: Date: Chapter 07 20. In stratified sampling, the population is divided into relatively homogeneous subsets called strata, and then random samples are taken from each stratum. a. True b. False 21. In stratified sampling with proportional sample sizes, the proportion of each stratum selected differs from stratum to stratum. a. True b. False 22. In cluster sampling, the population is divided into subsets called clusters (such as cities or city blocks), and then a random sample of the clusters is selected. Once the clusters are selected, we typically sample all of the members in each selected cluster. a. True b. False 23. Which of the following statements correctly describe estimation? a. It is the process of inferring the values of known population parameters from those of unknown sample statistics. b. It is the process of inferring the values of unknown sample statistics from those of known population parameters. c. It is the process of inferring the values of known sample statistics from those of unknown population parameters. d. It is the process of inferring the values of unknown population parameters from those of known sample statistics. 24. A sampling error is the result of: a. measurement error b. nonresponse bias c. nontruthful responses d. bad luck 25. The standard deviation of is usually called the a. standard error of the mean b. standard error of the sample c. standard error of the population d. randomized standard error Copyright Cengage Learning. Powered by Cognero. Page 4 Name: Class: Date: Chapter 07 26. When a portion of the sample does not respond to the survey, results. a. measurement error b. nonresponse bias c. sampling error d. systematic failure e. nonlinear error 27. The accuracy of the point estimate is measured by its: a. standard deviation b. standard error c. sampling error d. nonsampling error 28. The sampling mean is the estimate for the population mean . a. random b. point c. simple d. interval 29. Non-truthful response is a particular problem when: a. sensitive questions are asked. b. surveys are anonymous. c. interviewers are not trained. d. the sample is from an unusual population. 30. Measurement error occurs when: a. a portion of the sample does not respond to the survey b. the sample responses are not clear c. the responses to question do not reflect what the investigator had in mind d. the investigator does not correctly tally all responses 31. The two basic sources for error when using random sampling are: a. sampling and selection b. identification and selection c. sampling and nonsampling d. bias and randomness e. linear and nonlinear Copyright Cengage Learning. Powered by Cognero. Page 5 Name: Class: Date: Chapter 07 32. Sampling error is evident when: a. a question is poorly worded b. the sample is too small c. the sample is not random d. the sample mean differs from the population mean 33. The opportunity for sampling error is decreased by: a. larger sample sizes b. smaller sample sizes c. affluent samples d. educated samples 34. The theorem that states that the sampling distribution of the sample mean is approximately normal when the sample size n is reasonably large is known as the: a. central limit theorem b. central tendency theorem c. simple random sample theorem d. point estimate theorem 35. There is approximately % chance that any particular will be within two standard deviations of the population mean ( ). a. 90 b. 95 c. 99 d. 99.7 36. Which of the following statements are correct? a. A point estimate is an estimate of the range of a population parameter b. A point estimate is a single value estimate of the value of a population parameter c. A point estimate is an unbiased estimator if its standard deviation is the same as the actual value of the population standard deviation d. All of these options 37. An unbiased estimator is a: a. sample statistic used to approximate a population parameter b. sample statistic, which has an expected value equal to the value of the population parameter c. sample statistic whose value is usually less than the population parameter d. standard error of the mean Copyright Cengage Learning. Powered by Cognero. Page 6 Name: Class: Date: Chapter 07 38. Which of the following statements are correct? a. A confidence interval describes a range of values that is likely not to include the actual population parameter b. A confidence interval is an estimate of the range for a sample statistic. c. A confidence interval is an estimate of the range of possible values for a population parameter. d. None of these options 39. The approximate standard error of the sample mean is calculated as: a. b. c. d. 40. The approximate 95% confidence interval for a population mean is: a. b. c. d. 41. The finite population correction factor, , should generally be used when: a. N is any finite size b. n is less than 5% of the population size N c. n is greater than 5% of the population size N d. n is any finite size 42. The Central Limit Theorem (CLT) is generally valid for: a. n > 5 b. n > 10 c. n > 20 d. n > 30 e. any size n Copyright Cengage Learning. Powered by Cognero. Page 7 Name: Class: Date: Chapter 07 43. The averaging effect means that as you average more and more observations from a given distribution, the variance of the average a. increases b. decreases c. is unaffected d. could either increase, decrease or stay the same 44. When we sample less than 5% of the population, the finite population correction factor; fpc = , is used to modify the formula for the standard error of the sample mean. a. True b. False 45. A point estimate is a single numeric value, a “best guess” of a population parameter, calculated from the sample data. a. True b. False 46. The difference between the point estimate and the true value of the population parameter being estimated is called the estimation error. a. True b. False 47. A confidence interval is an interval calculated from the population data, where we strongly believe the true value of the population parameter lies. a. True b. False 48. The sampling distribution of any point estimate (such as the sample mean or proportion) is the distribution of the point estimates we would obtain from all possible samples of a given size drawn from the population. a. True b. False 49. An unbiased estimate is a point estimate such that the mean of its sampling distribution is equal to the true value of the population parameter being estimated. a. True b. False Copyright Cengage Learning. Powered by Cognero. Page 8 Name: Class: Date: Chapter 07 50. The standard error of an estimate is the standard deviation of the sampling distribution of the estimate. It measures how much estimates from different samples vary. a. True b. False 51. Ideally, we prefer estimates that have large standard errors. a. True b. False 52. It is customary to approximate the standard error of the sample mean by substituting the sample standard deviation s for in the formula: SE( ) = . a. True b. False 53. An estimator is said to be unbiased if the mean of its sampling distribution equals the value of the population parameter being estimated. a. True b. False 54. Estimation is the process of inferring the value of an unknown population parameter using data from a random sample a. True b. False 55. The Central Limit Theorem (CLT) states that the sampling distribution of the mean is approximately normal, no matter what the distribution of the population, so long as the sample size is large enough. a. True b. False 56. The averaging effect says that as you average more and more observations from a given distribution, the variance of the average increases. a. True b. False Copyright Cengage Learning. Powered by Cognero. Page 9 Name: Class: Date: Chapter 07 57. We can measure the accuracy of judgmental samples by applying some simple rules of probability. This way, judgmental samples are not likely to contain our built-in biases. a. True b. False 58. The probability of being chosen in a simple random sample of size n from a population of size N is: a. 1/N b. N – 1/n c. N/n d. n/N 59. The key to using stratified sampling is: a. identifying the strata b. selecting the appropriate strata c. defining the strata d. randomizing the strata 60. If systematic sampling is chosen as the sampling technique, it is probably because: a. Systematic sampling has better statistical properties than simple random sampling b. Systematic sampling is more convenient c. Systematic sampling always results in more representative sampling than simple random sampling d. None of these options 61. The primary advantage of cluster sampling is sampling convenience (and possibly less cost). The downside, however, is that the inferences drawn from a cluster sample can be less accurate, for a given sample size, than for other sampling plans. a. True b. False 62. If a simple random sample of size n is chosen from a population of size N, then each member of the population has probability N / n of being chosen in the sample. a. True b. False 63. Simple random sampling can result in under-representation or over-representation of certain segments of the population. This is one of several reasons that simple random samples are almost never used in real applications. a. True b. False Copyright Cengage Learning. Powered by Cognero. Page 10 Name: Class: Date: Chapter 07 64. Stratified samples are typically not used in real applications because they provide less accurate estimates of population parameters for a given sampling cost. a. True b. False 65. Cluster sampling is often less convenient and more costly than other random sampling methods. a. True b. False 66. One obvious advantage of stratified sampling is that we obtain separate estimates within each stratum – which we would not obtain if we took a simple random sample from the entire population. A more important advantage is that we can increase the accuracy of the resulting population estimates by using appropriately defined strata. a. True b. False 67. Systematic sampling is generally similar to simple random sampling in its statistical properties. a. True b. False 68. The mean of the sampling distribution of always equals a. the population mean b. / n c. the population standard deviation d. / n 69. The opportunity for nonsampling error is increased by: a. larger sample sizes b. smaller sample sizes c. affluent samples d. educated samples 70. The reason the Central Limit Theorem (CLT) is such an important result in statistics is because: a. The CLT allows us to assume that the population distribution is approximately normal, provided n is reasonably large b. The CLT allows us to estimate the population mean without knowing the exact form of the population distribution, provided n is reasonably large c. The CLT allows us to construct confidence intervals for the population mean without knowing the exact form of the population distribution, provided n is reasonably large d. All of these options Copyright Cengage Learning. Powered by Cognero. Page 11 Name: Class: Date: Chapter 07 71. A sample of size 20 is selected at random from a population of size N. If the finite population correction factor is 0.9418, then N must be 169. a. True b. False 72. The sampling distribution of the mean will have the same mean as the original population from which the samples were drawn. a. True b. False 73. The sampling distribution of the mean will have the same standard deviation as the original population from which the samples were drawn. a. True b. False 74. The randomized response technique is a way of getting at sensitive information to avoid estimation errors due to nontruthful responses. a. True b. False 75. Voluntary response bias occurs when the responses to questions do not reflect what the investigator had in mind. a. True b. False 76. If the sample size is greater than 30, the Central Limit Theorem (CLT) will always apply. a. True b. False 77. The Central Limit Theorem (CLT) says that as long as the sample size is reasonably large, there is about a 95% chance that the magnitude of the sampling error for the mean will be no more than two standard errors. a. True b. False Copyright Cengage Learning. Powered by Cognero. Page 12 Name: Class: Date: Chapter 07 78. The size of a sample can be selected by first determining the desired standard error and then using the formula to calculate n. a. True b. False 79. Consider the frame of 50 full-time employees of Computer Technologies, Inc (CTI). CTI’s human resources manager has collected annual salary figures for all employees and she has calculated a mean of $47,723, a median of $41,082 and a standard deviation of $24,167. A simple random sample of 10 employees is presented below (salary is in $1,000’s). Compute the mean, median, and standard deviation for the sample and compare these statistics with the measures for the entire company. Employee 1 2 3 4 5 6 7 8 9 10 Salary 38.8 46.7 61.1 49.6 58.5 78.8 36.7 46.5 47.6 56.7 Current annual salaries: Number of years of post-secondary education: Copyright Cengage Learning. Powered by Cognero. Page 13 Name: Class: Date: Chapter 07 80. (A) Compute the mean, median, and standard deviation of the annual salaries for the 52 employees in the given frame. (B) Use Excel to choose a systematic sample of size 13 from the frame of annual salaries. (C) Compute the mean, median, and standard deviation of the annual salaries for the 13 employees included in your systematic sample in (B) (D) Compare your statistics in (C) with your computed descriptive measures for the frame in (A). Is your systematic sample representative of the frame with respect to the annual salary variable? (E) Assume that we wish to stratify these employees by the number of years of post-secondary education, select such a stratified sample of size 15 with approximately proportional sample sizes. (F) Compute the mean, median, and standard deviation of the annual salaries for the 15 employees included in your stratified sample in (E). (G) Compare these statistics in (F) with your computed descriptive measures for the frame obtained in (A). Is your stratified sample representative of the frame with respect to the annual salary variable? (C) Copyright Cengage Learning. Powered by Cognero. Page 14 Name: Class: Date: Chapter 07 (D) After generating the summary measures for both the frame and the sample, we can conclude that the sample does not represent the frame well. The mean, median, and standard deviation of the frame are all much smaller than the mean, median, and standard deviation of the sample. (E) This portion of the solution involves several steps. First, we noted the total sample size needed. Second, we developed the strata we will use to separate the given frame: in this case we placed every two years in a new stratum as shown below. Next, we generated a column labeled "Category", to place a number between 1 and 5 next to the salary that corresponds with the stratum of that number. For example, if the annual salary was of a person who only had 2 years of education beyond secondary education, then a number 2 for Stratum 2 was placed next to the salary. The "Category" column was generated using an IF statement. We then unstacked the categories in order to count the number of salaries in each stratum. This was done by using StatTools's Data Utilities/Unstack function. Once this was completed, we used Excel's COUNT function to count the number of values in each stratum and then generated proportional numbers for each stratum with respect to the size of the given population. Once the proportions are generated, we used an Excel's random number function to assign a random number to each salary. Then, by using Excel to sort the salaries in each stratum by their random number (in this case by ascending number) we selected the salaries in each stratum that will be included in the sample. These salaries are shown below. Copyright Cengage Learning. Powered by Cognero. Page 15 Name: Class: Date: Chapter 07 (F) (G) When looking at the mean, median, and standard deviation of both the sample and population, we can conclude that the stratified sample represents the population fairly well, although the summary measures are all slightly lower than those of the population. 81. A sales manager for a company that makes commercial ovens for restaurants is interested in estimating the average number of restaurants in all metropolitan areas across the entire country. He does not have access to the data for each metropolitan location, so he had decided to select a sample that will be representative of all such areas, and will use a sample size of 30. Do you believe that simple random sampling is the best approach to obtaining a representative subset of the metropolitan areas in the given frame? Explain. If not, recommend how the sales manager might proceed to select a better sample of size 30 from this data? Name: Class: Date: Chapter 07 Suppose that the average weekly earnings for employees in general automotive repair shops is $450, and that the standard deviation for the weekly earnings for such employees is $50. A sample of 100 such employees is selected at random. 82. (A) Find the mean and standard deviation of the sampling distribution of the average weekly earnings in the sample. (B) Find probability that the mean of the sample is less than $445. (C) Find the probability that the mean of the sample is between $445 and $455. (D) Find the probability that the mean of the sample is greater than $460. (E) Explain why the assumption of normality about the distribution of the average weekly earnings for employees was not involved in the answers to (A) through (D). ANSWER: (A) E( ) = = 450, and SE( ) = = 5 (B) P( < 445) = P(Z < -1) = 0.5000 – 0.3413 = 0.1587 (C) P(445< <455) = P(-1.0 < Z < 1.0) = 2(0.3413) = 0.6826 (D) P( > 460) = P(Z > 2.0) = 0.5000 – 0.4772 = 0.0228 (E) The sample size is large; n = 100 is greater than 30, so the distribution of the average weekly earnings for employees is at least approximately normal. Suppose that you are an entrepreneur interested in establishing a new Internet-based auction service. Furthermore, suppose that you have gathered basic demographic information on a large number of Internet users. You currently have information on 1000 individuals related to their gender, age, education, marital status, annual household income, and number of people in household. Assume that these individuals were carefully selected through stratified sampling. 83. (A) To assess potential interest in your proposed enterprise, you would like to conduct telephone interviews with a representative subset of the 1000 Internet users. How would you proceed to stratify the given frame of 1000 individuals to choose 50 for telephone interviews? Explain your approach. (B) Explain how you could apply cluster sampling to obtain a sample size of 50 from this frame. What are the advantages and disadvantages of employing cluster sampling in this case? Copyright Cengage Learning. Powered by Cognero. Page 17 Name: Class: Date: Chapter 07 An editor of a local newspaper is concerned with the number of errors that are found in the daily paper. In order to understand the extent of this problem, the editor would like to estimate the average number of errors in the daily paper. The frame in this case is the number of errors found in the daily paper for the past six months (180 issues). 84. (A) What sample size would be required for the production personnel to be approximately 95% sure that their estimate of the average number of errors per issue is within 4 errors of the true mean? Assume that the editor’s best estimate of the population standard deviation ( ) is 10 errors per issue. (B) How does your answer to (A) change if the editor wants the estimate to be within 3 errors of the actual population mean? Explain the difference in your answers to (A) and (B). Copyright Cengage Learning. Powered by Cognero. Page 18 Name: Class: Date: Chapter 07 85. (A) Using these 50 students as the frame, use Excel to generate a simple random sample of size 10 from this frame. (B) Compute the mean scores in the frame and the simple random sample you generated in (A). (C) Compare the mean scores you computed in (B). Is your simple random sample a good representative of the frame? Why or why not? (D) Using these 50 students as the frame, use Excel to generate a systematic sample of size 10 from this frame. (E) Compare the mean scores in the frame with that in the systematic sample in (D). What do you conclude? Copyright Cengage Learning. Powered by Cognero. Page 19 Name: Class: Date: Chapter 07 A university bookstore manager is mildly concerned about the number of textbooks that were under-ordered and thus unavailable two days after the beginning of classes. The manager instructs an employee to pick a random number, go to the place where that number book is shelved, examine the next 50 titles, and record how many titles are unavailable. 86. (A) Technically, this process does not yield a random sample of the books in the store. Why not? (B) How could a truly random sample be obtained? 87. (A) Do you think she has obtained a true random sample? (B) What average price could she report, based on the above sample? (C) What average price range could she report, based on the above sample? (D) Do you see any issues with reporting the range calculated for (C)? Copyright Cengage Learning. Powered by Cognero. Page 20 Name: Class: Date: Chapter 07 · The selling price of each house (in thousands of dollars) · The size of each house (in hundreds of square feet) · The number of bedrooms in each house Copyright Cengage Learning. Powered by Cognero. Page 21 Name: Class: Date: Chapter 07 88. (A) Suppose that Sally wishes to examine a representative subset of these 60 houses that has been stratified by the number of bedrooms. Use Excel to assist her by finding such a stratified sample of size 10 with proportional sample sizes. (B) Explain how Sally could apply cluster sampling in selecting a sample of size 15 from this frame. (C) What are the advantages and disadvantages of employing cluster sampling in this case? Copyright Cengage Learning. Powered by Cognero. Page 22 Name: Class: Date: Chapter 07 $75.30 $614.11 $696.34 $572.08 $748.23 $21.20 $99.79 $1,233.38 $530.40 $378.37 $596.14 $239.65 $2,995.38 $1,069.06 $929.80 $259.98 $123.65 $68.92 $192.35 $754.45 $309.00 $163.31 $71.75 $904.92 $40.70 $161.12 $459.38 $171.48 $402.81 $157.44 $41.81 $87.08 $489.97 $468.12 $400.57 $319.40 $533.82 $1,801.35 $1,666.50 $37.16 $85.92 $91.43 $193.14 $106.95 $214.62 $10.62 $582.18 $39.65 $123.66 $76.33 $291.73 $398.48 $659.18 $101.24 $1,740.47 $322.26 $1,509.34 $1,599.04 $358.62 $492.05 $1,052.68 $596.33 $100.54 $1,288.70 $421.46 $1,799.51 $581.21 $571.63 $180.58 $98.82 $358.68 $38.93 $874.78 $2,761.93 $750.44 $376.60 $269.48 $456.79 $216.81 $305.49 Copyright Cengage Learning. Powered by Cognero. Page 23 Name: Class: Date: Chapter 07 89. (A) What sample size would be required for the auditors to be approximately 95% sure that their estimate of the average savings account balance at this bank is within $150 of the true mean? Assume that their best estimate of the population standard deviation is $300. (B) Choose a simple random sample of the size found in (A). (C) Compute the observed sampling error based on the sample you have drawn from the population. How does the actual sampling error compare to the maximum possible probable absolute error established in (A)? Explain ANSWER: (A) (B) The simple random sample of size 16 was generated using StatTool’s Random Sample tool in the Data Utilities section. Next, the VLOOKUP function was used to place the appropriate balances next to the customers that were selected to be included in the sample. The following sample was obtained. Customer Balance 40 456.79 51 193.14 63 239.65 37 1799.51 8 402.81 20 269.48 42 99.79 39 2761.93 78 38.93 3 530.40 35 1599.04 64 259.98 14 659.18 32 10.62 11 85.92 68 87.08 (C) Based on the above sample (results will differ): The sample mean = $593.39 The frame mean = $537.31 The sampling error is the difference between the sample mean and the frame mean. In this case, the sampling error is $56.08, which is much less than the maximum probable absolute error of $150. This is the case because the maximum probable absolute error is, by definition, the largest possible amount that will still give 95% certainty. As illustrated here, the observed sampling error is smaller than the largest possible error. Copyright Cengage Learning. Powered by Cognero. Page 24 Name: Class: Date: Chapter 07 90. A cannery claims that its sardine cans have a net weight of 8 oz., with a standard deviation of 0.1 oz. You take a simple random sample of 30 cans and encounter a sample mean of 7.85 oz. Are you inclined to believe the claim? ANSWER: The sampling distribution of is normal (since n 30) with mean and standard deviation given by E( ) = = 8, and SE( ) = = 0.0183, respectively. Therefore, P( < 7.8) = P(Z < -8.2) = 0. If the claim were true, such a sample would not be encountered. The cannery management is not telling the truth. The manager of a local fast-food restaurant is interested in improving service provided to customers who use the restaurant’s drive-up window. As a first step in the process, the manager asks his assistant to record the time (in minutes) it takes to serve a large number of customers at the final window in the facility’s drive-up system. The given frame in this case is 200 customer service times observed during the busiest hour of the day for this fast-food restaurant. The frame of 200 service times yielded a mean of 0.881. A simple random sample of 10 from this frame is presented below. Customer 1 2 3 4 5 6 7 8 9 10 Service time 1.02 1.18 0.95 0.90 0.85 1.10 0.75 0.60 1.25 1.00 91. (A) Compute the point estimate of the population mean from the sample above. What is the sampling error in this case? Assume that the population consists of the given 200 customer service times. (B) Compute the point estimate of the population standard deviation from the sample above. (C) Should you use the finite population correction (fpc) factor to estimate the standard error of ? Explain. If your answer is yes, what is the value of the fpc? (D) Determine a good approximation to the standard error of the mean in this case. Copyright Cengage Learning. Powered by Cognero. Page 25 Name: Class: Date: Chapter 07 A battery manufacturer wants to estimate the average number of defective (or dead) batteries contained in a box shipped by the company. Production personnel at this company have recorded the number of defective batteries found in each of the 2000 boxes shipped in the past week. 92. (A) What sample size would be required for the production personnel to be approximately 95% sure that their estimate of the average number of defective batteries per box is within 0.3 unit of the true mean? Assume that the best estimate of the population standard deviation ( ) is 0.9 defective batteries per box. (B) How does your answer to (A) change if the production personnel want their estimate to be within 0.5 unit of the actual population mean? Evaluate the tradeoff between required accuracy and sample size requirement for this case and the case in (A). Copyright Cengage Learning. Powered by Cognero. Page 26 Name: Class: Date: Chapter 07 [Show More]

Last updated: 2 years ago

Preview 1 out of 26 pages