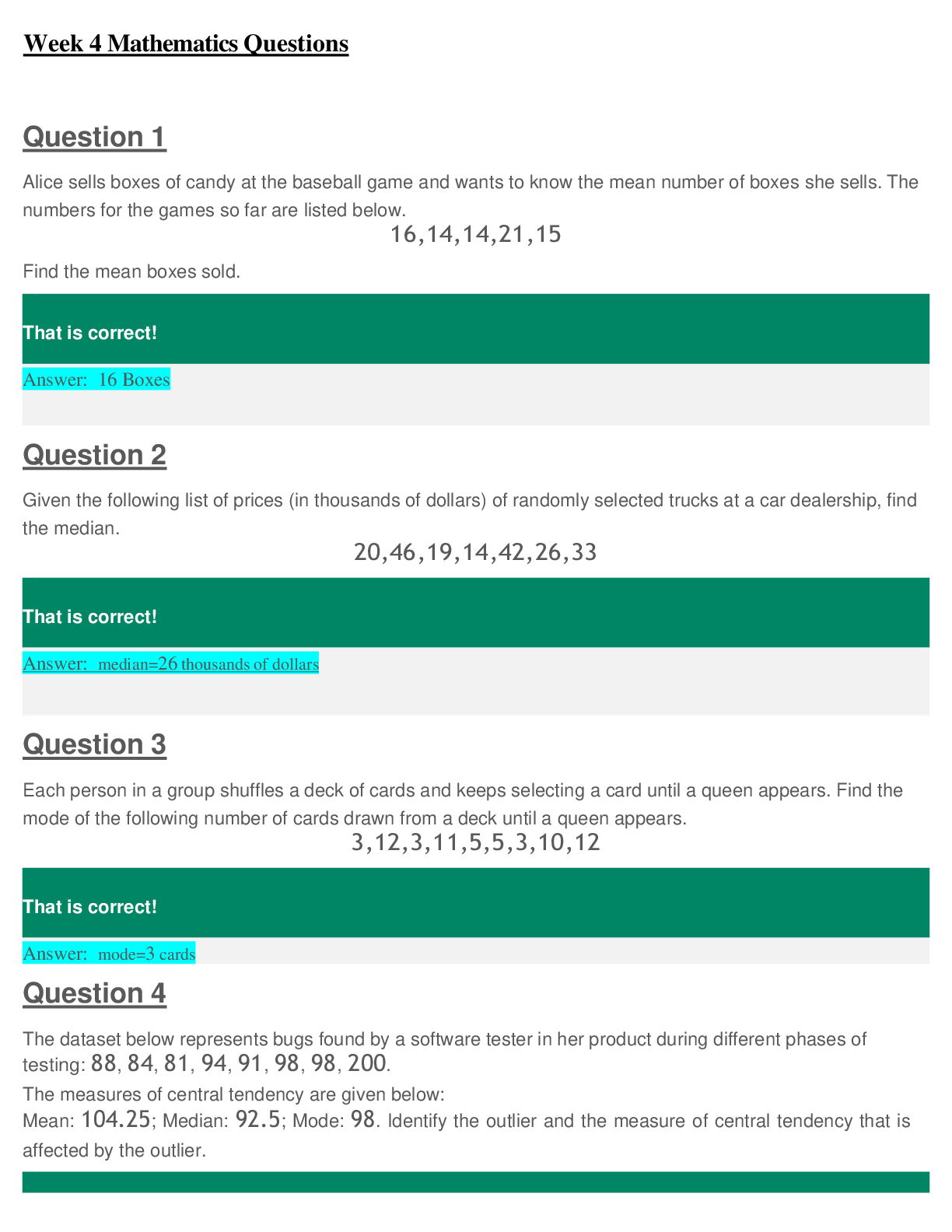
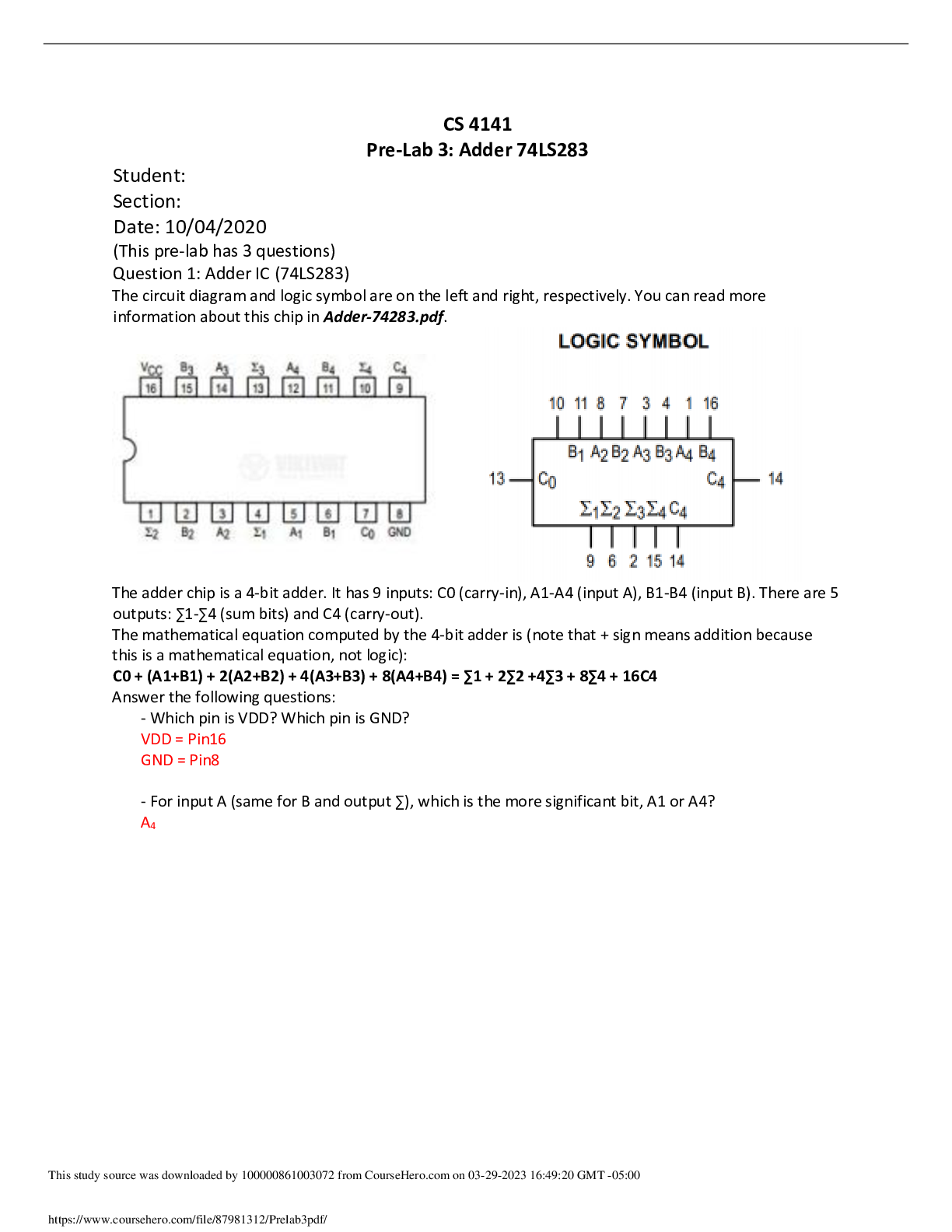
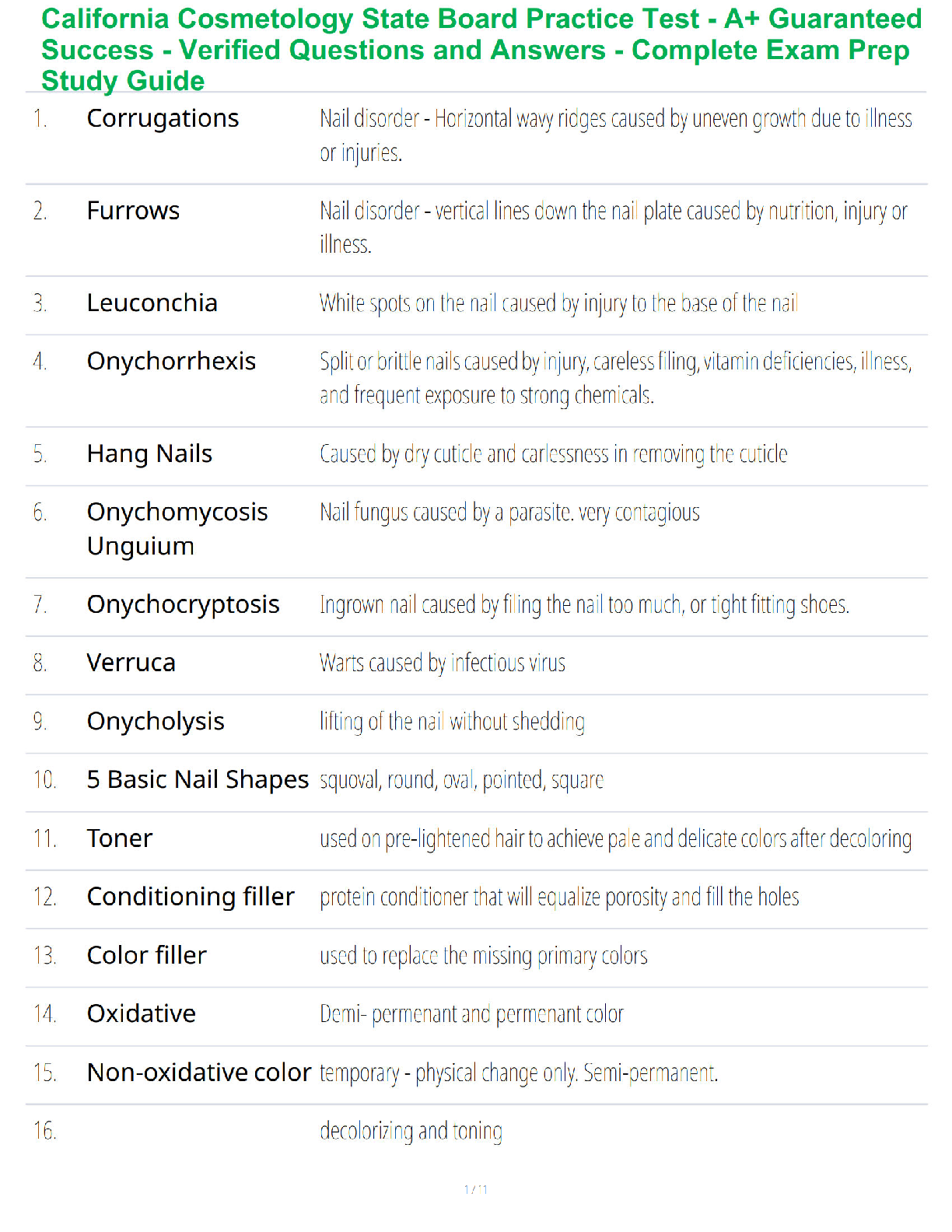
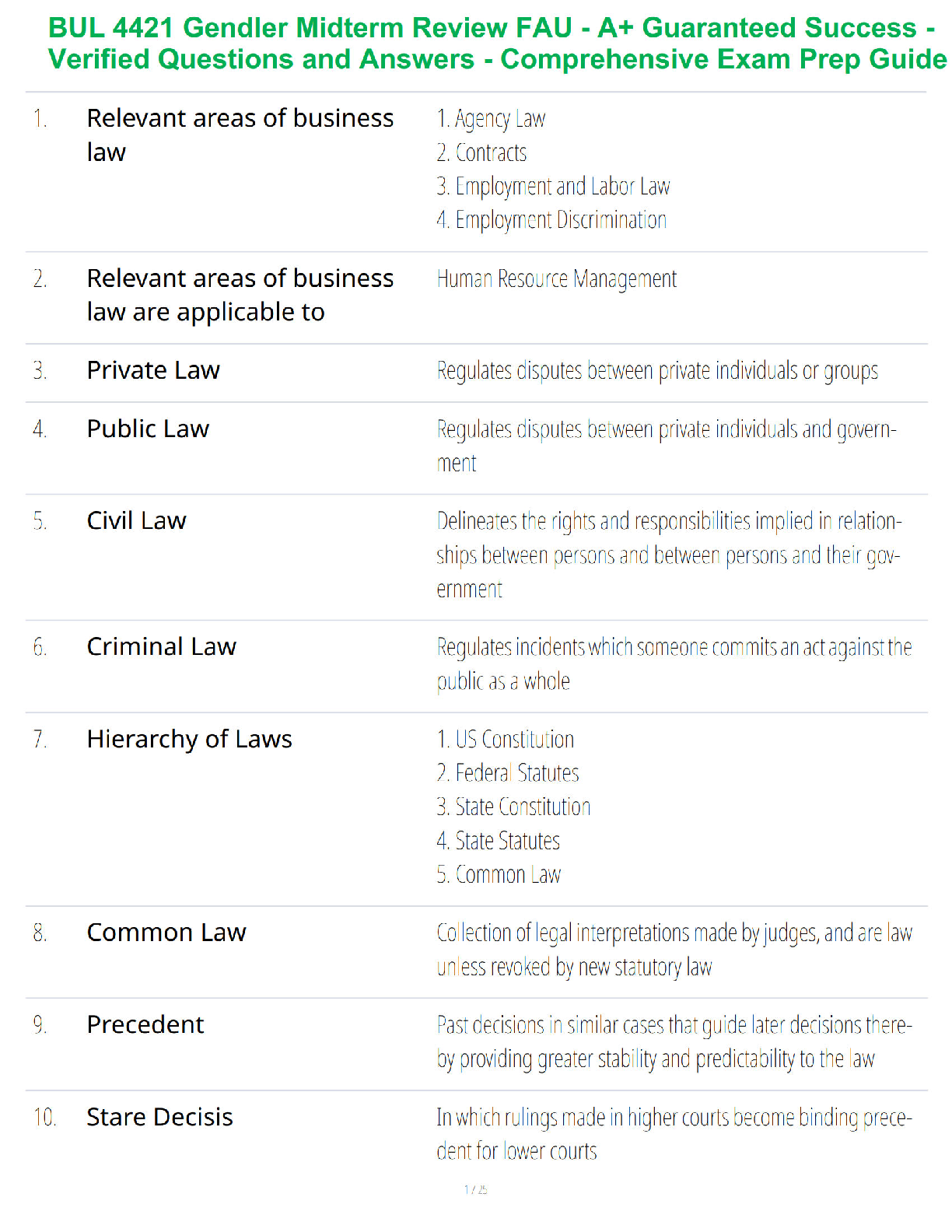
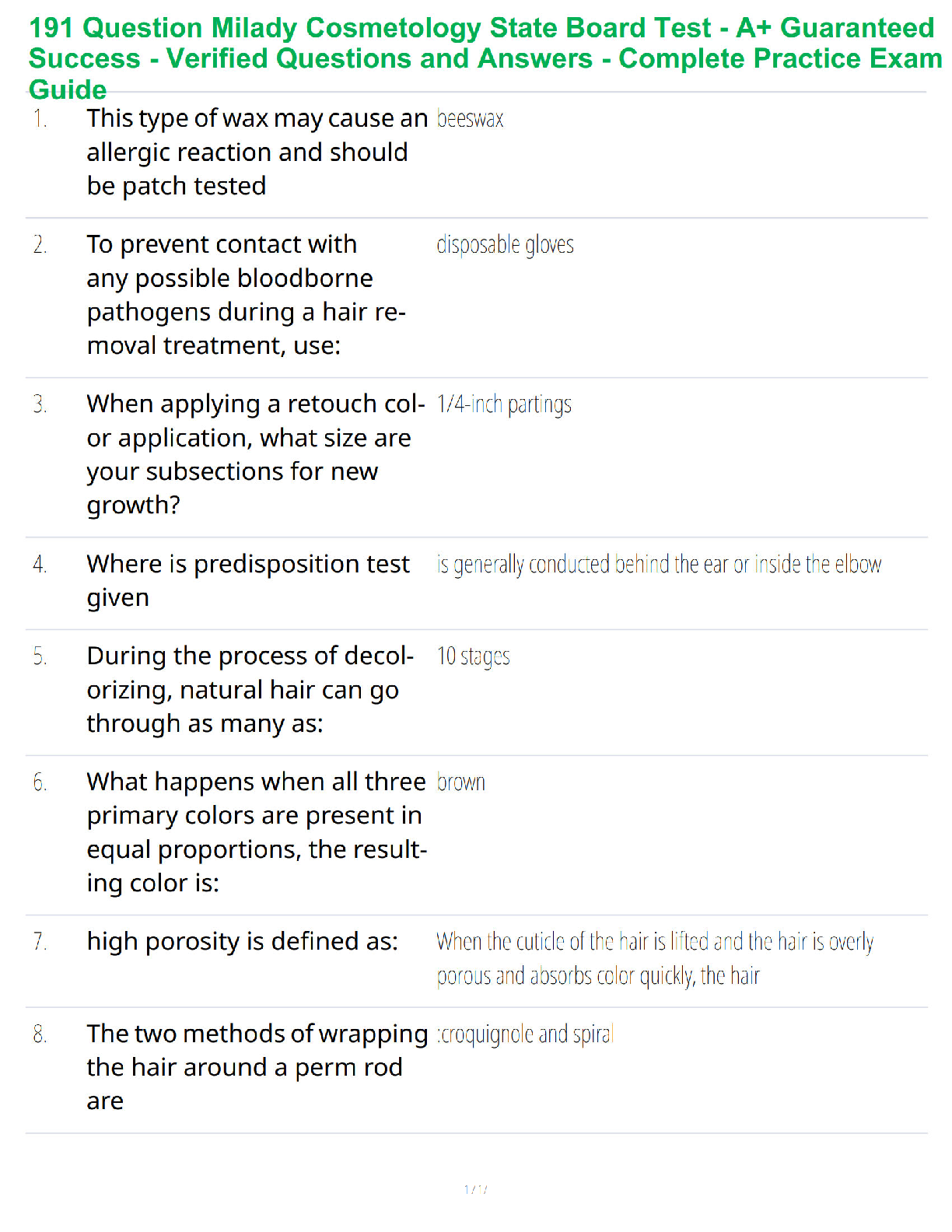
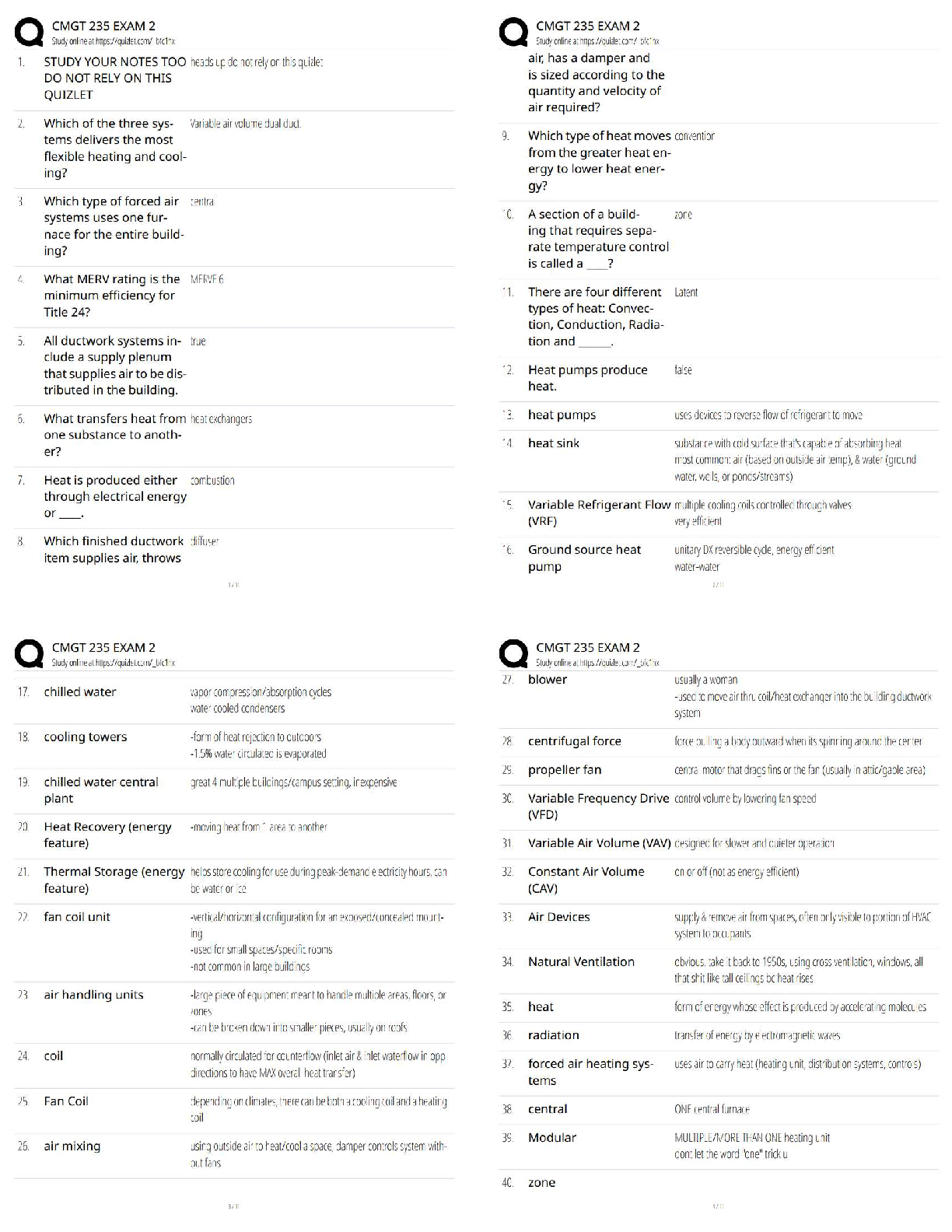
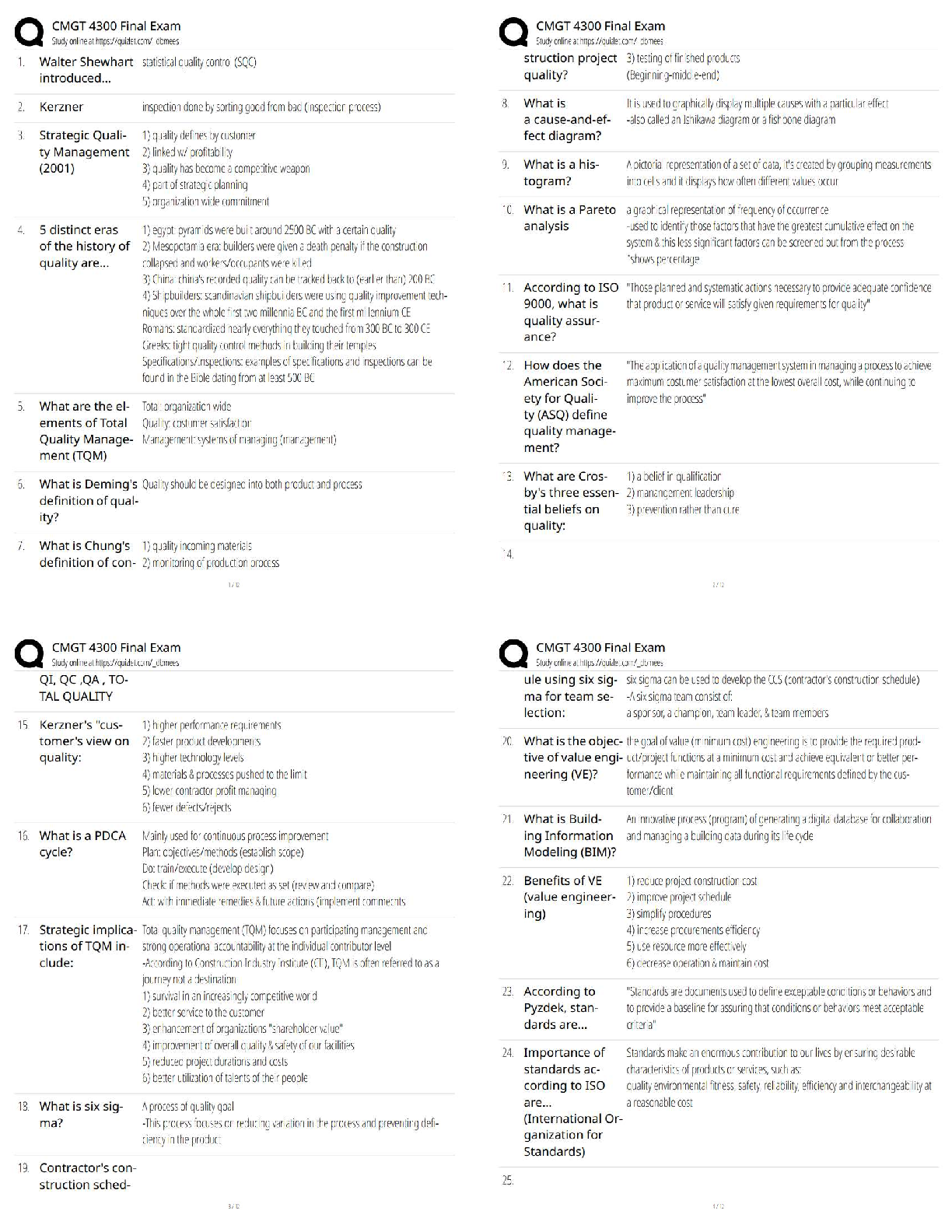
Tutorial-3
Coupled Oscillator
Problem 1
There are two small massive beeds, each of mass ?, on a taut massless string of
length 8?, as shown. The tension in the string is ?.
1. Derive expressions for the normal mode
...
Tutorial-3
Coupled Oscillator
Problem 1
There are two small massive beeds, each of mass ?, on a taut massless string of
length 8?, as shown. The tension in the string is ?.
1. Derive expressions for the normal mode angular frequencies of the system,
for small displacements of the system in a plane. Assume that ? is
suffieciently large that you may ignore gravity.
2. If at ? = 0 both masses are stationary, one is at equilibrium and the other
displaced from equilibrium by a distance ?, write an expression for
displacement ?1(?) as a function of time of the mass initially in the
equilibrium p Problem 2
The figure above shows a system of masses in the x-y plane. The mass of 2? is
connected to an immobile wall with a spring of constant 2?, while the mass of ? is
connected to an immobile wall with a spring of constant ?. The masses are then
coupled to each other with an elastic band of length ?, under tension ? = 2??. The
masses are constrained to move in the x direction only. At equilibrium the masses
have the same x position and the springs are uncompressed. There is no friction orgravity. The displacements from equilibrium are small enough (?1, ?2 ≪ ?), so that
the tension in the band stays constant.
1. Find the normal mode frequencies of the system.
2. What are the ratios of the displacements from equilibrium for two different
normal modes? (Hint: Basically, you have to find out the eigen functions for
corresponding normal mode frequencies)
Problem 3
Two identical spring-mass systems ? and ? are coupled by a weak middle spring
having a spring constant smaller by a factor of 100 (i.e. 100??????? = ?? = ??).Mass ? is pulled by a small distance and released from rest, while mass ? is released
from rest at its equilibrium position, at ? = 0. Calculate the approximate number of
oscillations completed by mass ? before its oscillations die down first. Problem 4
Three identical masses ? are connected in series to four identical springs each of
force constant ? (each mass coupled to two strings, and the end springs to walls):
a) Calculate the eigenfrequencies of small oscillations (normal modes) of this
coupled oscillator system.
b) What sets of initial displacements would you give to the three masses so that
the system oscillates in each of these normal modes.
[Show More]