Questions and Answers > Statistics for MFEs_Problem_Set_4_Answers. University of California, Berkeley STAT 134

Document Content and Description Below

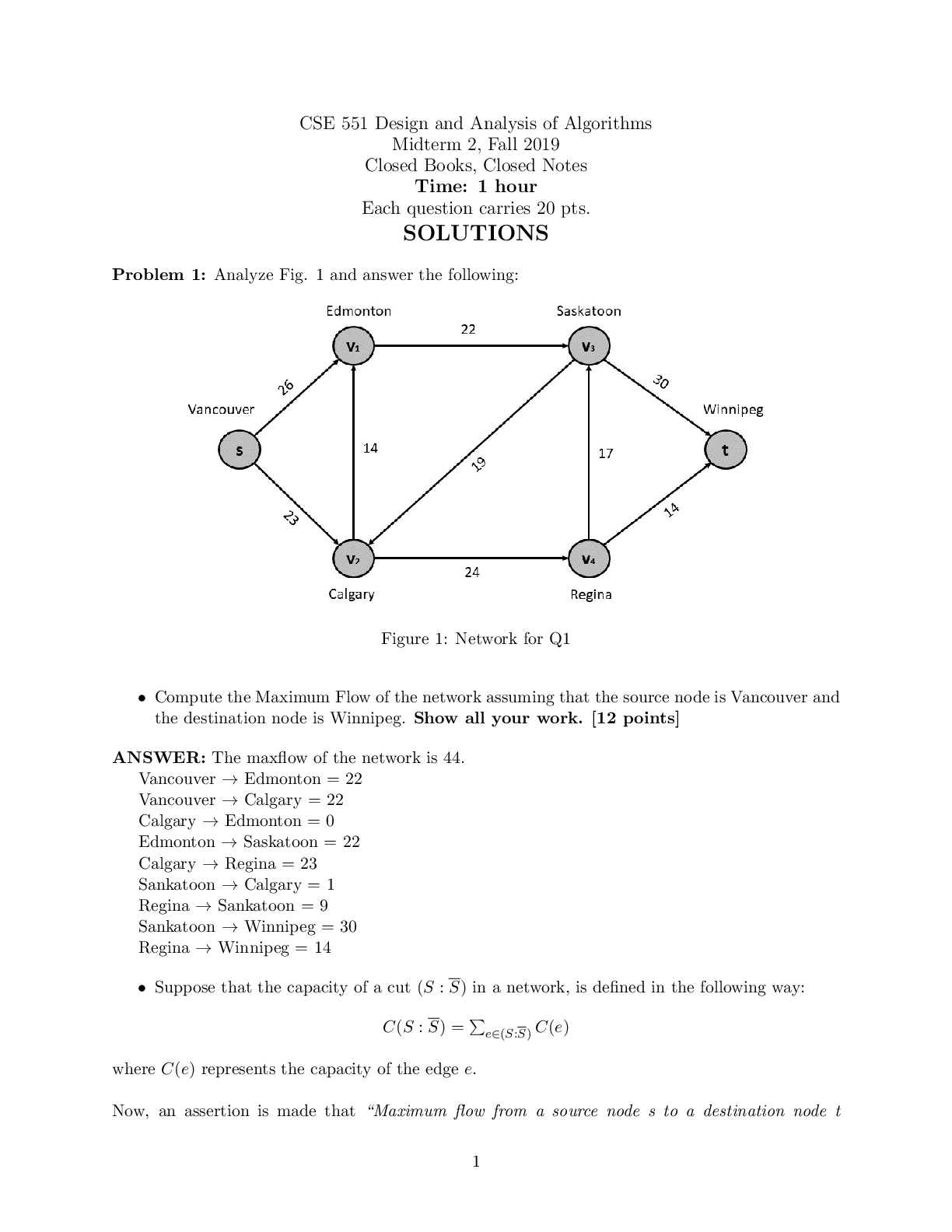
Statistics for MFEs – Problem Set 4 1. DGS ch. 6.2, problem 6: Suppose that X1,...,Xn form a random sample of size n from a distribution for which the mean is 6.5 and the variance is 4. Determine ... how large the value of n must be in order for the following relation to be satisfied: Given the mean is 6.5 for the distribution, we subtract 6.5 from each component in the inequality 2. DGS ch. 6.2, problem 14: Let f be a p.f. for a discrete distribution. Suppose that f (x) = 0 for x ¿∈ [0, 1]. Prove that the variance of this distribution is at most 1/4. Hint: Prove that there is a distribution supported on just the two points {0, 1} that has variance at least as large as f does and then prove that the variance of a distribution supported on {0, 1} is at most 1/4. Given discrete distribution f(x) = 0 for x Suppose X is a random variable such that X ∈ {0, 1} and X has the probability function as f. On graphing p – p2, we see that it’s max value is ¼ at p=½. Hence Va Now, defining a distribution supported on the variable X ∈ Hence, Y can have a variance of at most 1/4. 3. DGS ch. 6.3, problem 6: Suppose that three girls A, B, and C throw snowballs at a target. Suppose also that girl A throws 10 times, and the probability that she will hit the target on any given throw is 0.3; girl B throws 15 times, and the probability that she will hit the target on any given throw is 0.2; and girl C throws 20 times, and the probability that she will hit the target on any given throw is 0.1. Determine the probability that the target will be hit at least 12 times. Using python code to find value, from scipy.stats import norm print(norm.cdf(1.594)) P (X≥ 12)=1-0.9445=0.0555 4. DGS ch. 6.3, problem 10: A random sample of n items is to be taken from a distribution with mean µ and standard deviation σ. a. Use the Chebyshev inequality to determine the smallest number of items n that must be taken in order to satisfy the following relation: Using the Chebyshev inequality, b. Use the central limit theorem to determine the smallest number of items n that must be taken in order to satisfy the relation in part a. approximately. Using central limit theorem, 5. Illustrate the Law of Large Numbers and the Central Limit Theorem for the tν-distribution for different values of ν. Write a Python notebook for the following simulation for a given value of ν. Start with ν = 100. [ (a) Draw M i.i.d. random samples of length N from the tν distribution. Start with M = 500 and N = 10000 but you should experiment with different values. (b) For each sample m = 1, . . . ,M, compute the sample means for the first n = 5, 10, 100, 500, 1000, 10000 draws of the sample. (c) For each n, compute the mean, standard deviation and variance of the sample means across the M samples. This yields means, standard deviations, and variances for each of the six different values of n. Report your results in a table. (d) For each n, plot the distributions of the M sample means. (e) Describe how these simulations relate to the LLN and the CLT. Be careful to distinguish the implications of the LLN and the CLT. (f) Repeat steps (a) to (e) for ν = 10, 5, 2, 1, 0.5. (g) How does the choice of ν affect the limiting behavior of the sample mean? 6. Let Be the i.i.d. random vectors with mean µ = (µ1, µ2)T and variance-covariance matrix 2 . Derive the limiting distribution of Yn. By the central limiting theorem, [Show More]

Last updated: 2 years ago

Preview 1 out of 5 pages