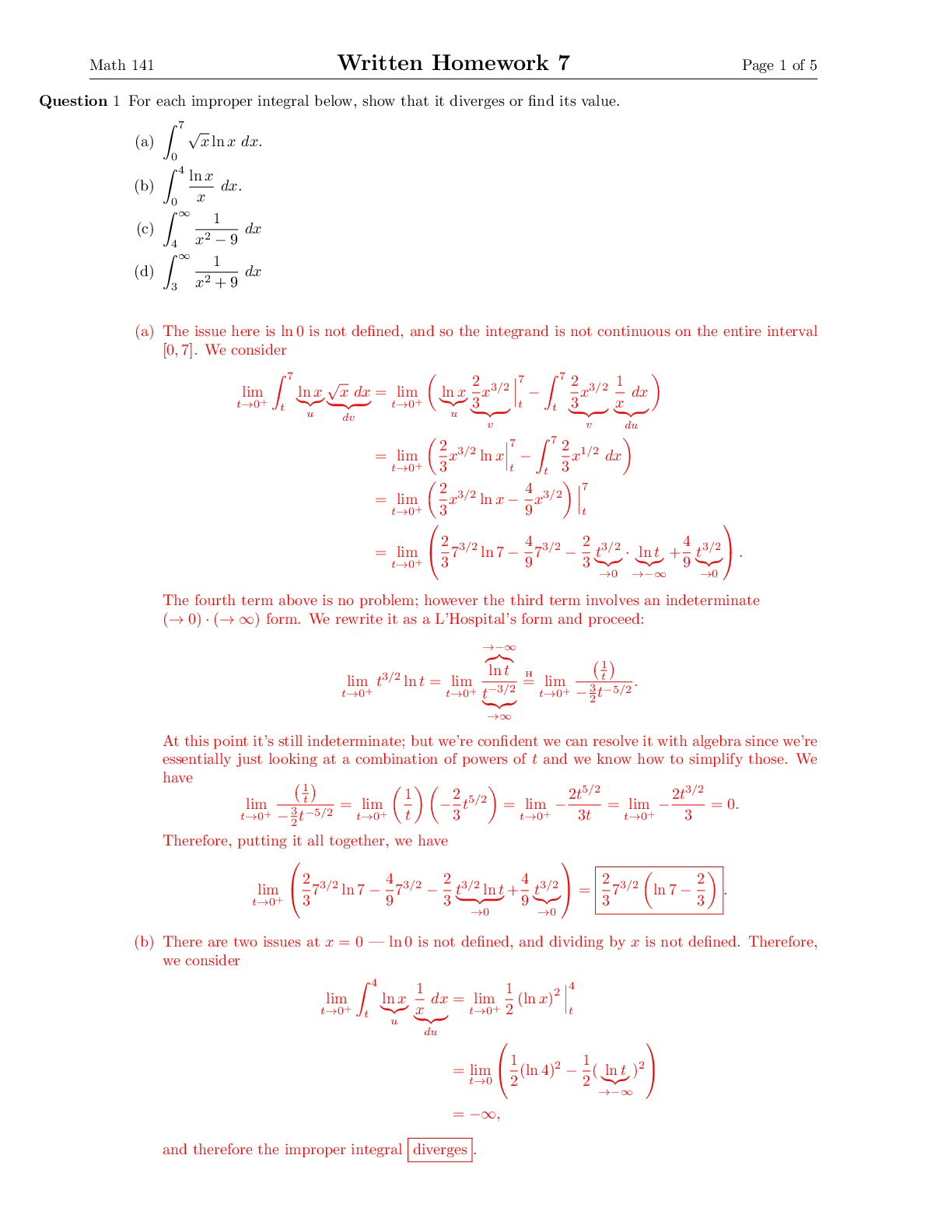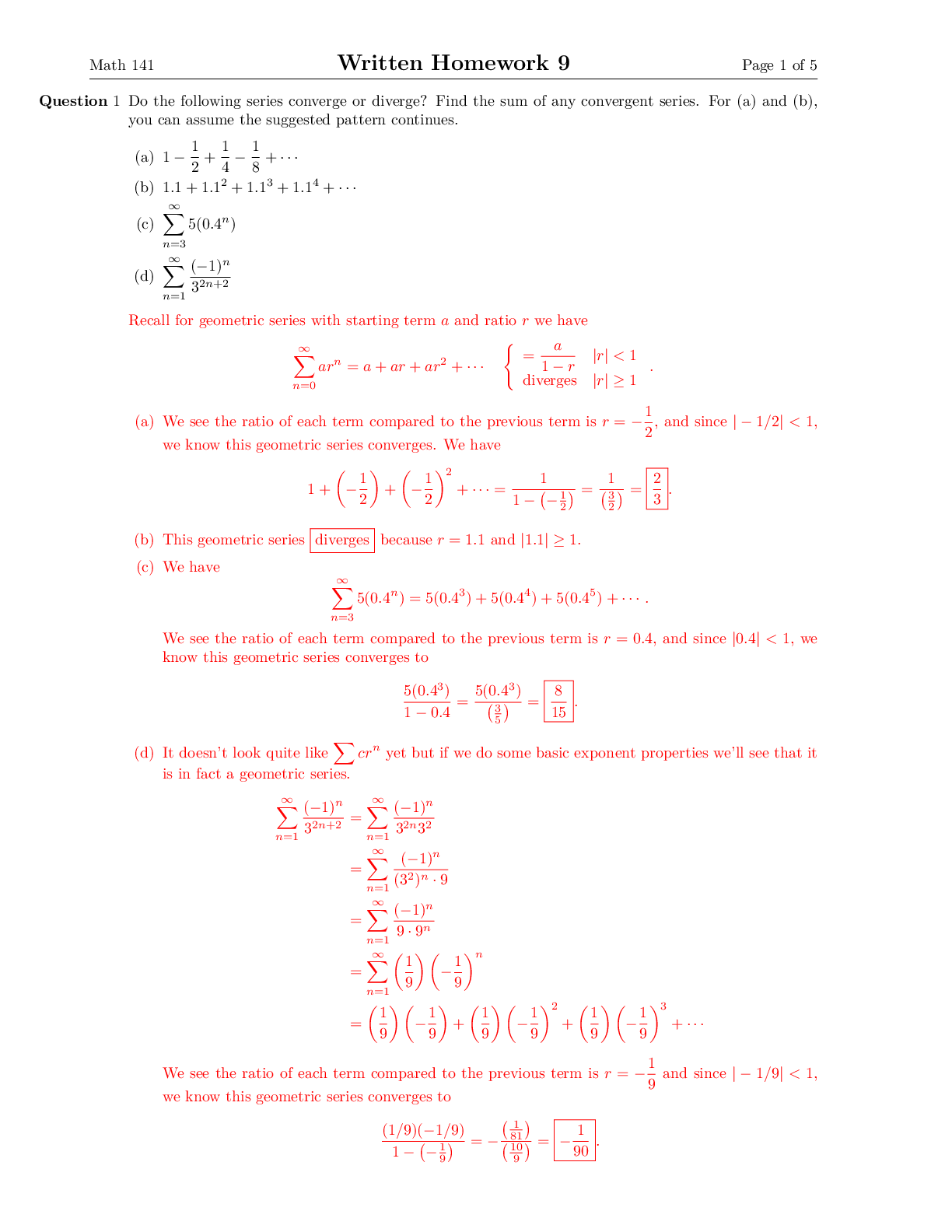Mathematics > QUESTIONS & ANSWERS > Homework Assignment 1 - Ohio State University MATH 3589 (All)

Homework Assignment 1 - Ohio State University MATH 3589

Document Content and Description Below

Math 3589 Spring 2016 Introduction to Financial Mathematics Homework Assignment #1 Due January 19 Solutions 1. Suppose S0 = 4, S1(H) = 8, S1(T) = 2 and r = 0. The price of a European Call option w... ith strike price k = 10 is V0 = 2. Using a replicating portfolio, explain why there exists an arbitrage opportunity. Solution There are many different ways we can construct a portfolio in which we will earn something at t = 1 when we start with nothing at t = 0. This is because at time t = 1 option is worth V1(H) = 0 = V1(T). In other words, if we use the replicating portfolio, we find that the risk-neutral price of the option is V0 = 0. Here is one example: We sell ∆0 units of the option, and invest ∆0V0 = 2∆0 dollars in the stock; i.e. we purchase ∆0/2 units of stock. At time t = 1, the option is worth zero, and therefore it is not exercised, and we have 4∆0 if S1(H) occurs and ∆0 if S1(T) occurs. This is arbitrage because we started with $0 and at t = 1, we had the possibility of making something without the possibility of losing anything. 2. We have a stock with S0 = 2, S1(H) = 3 and S1(T) = 1. The interest rate is r = .05. We wish to replicate a security that pays nothing if the coin is heads and 5 if it’s tails. What is the initial investment, and how much stock should we buy? Solution For the security, V , we have V1(H) = 0 and V1(T) = 5. The formula says V0 = 1 1 + r [˜pV1(H) + ˜qV1(T)] = 1 1.05 [.55 · 0 + .45 · 5] = 2.1429 . Thus, the price of the security is $2.14. This is the “initial investment”. Again, according to the formula, ∆0 = V1(H) − V1(T) S1(H) − S1(T) = −5 3 − 1 = −2.5 . Since ∆0 < 0 we should short-sell 2.5 shares of stock if we wish to replicate the security V . This m [Show More]

Last updated: 2 years ago

Preview 1 out of 3 pages

Buy Now

Instant download

We Accept: