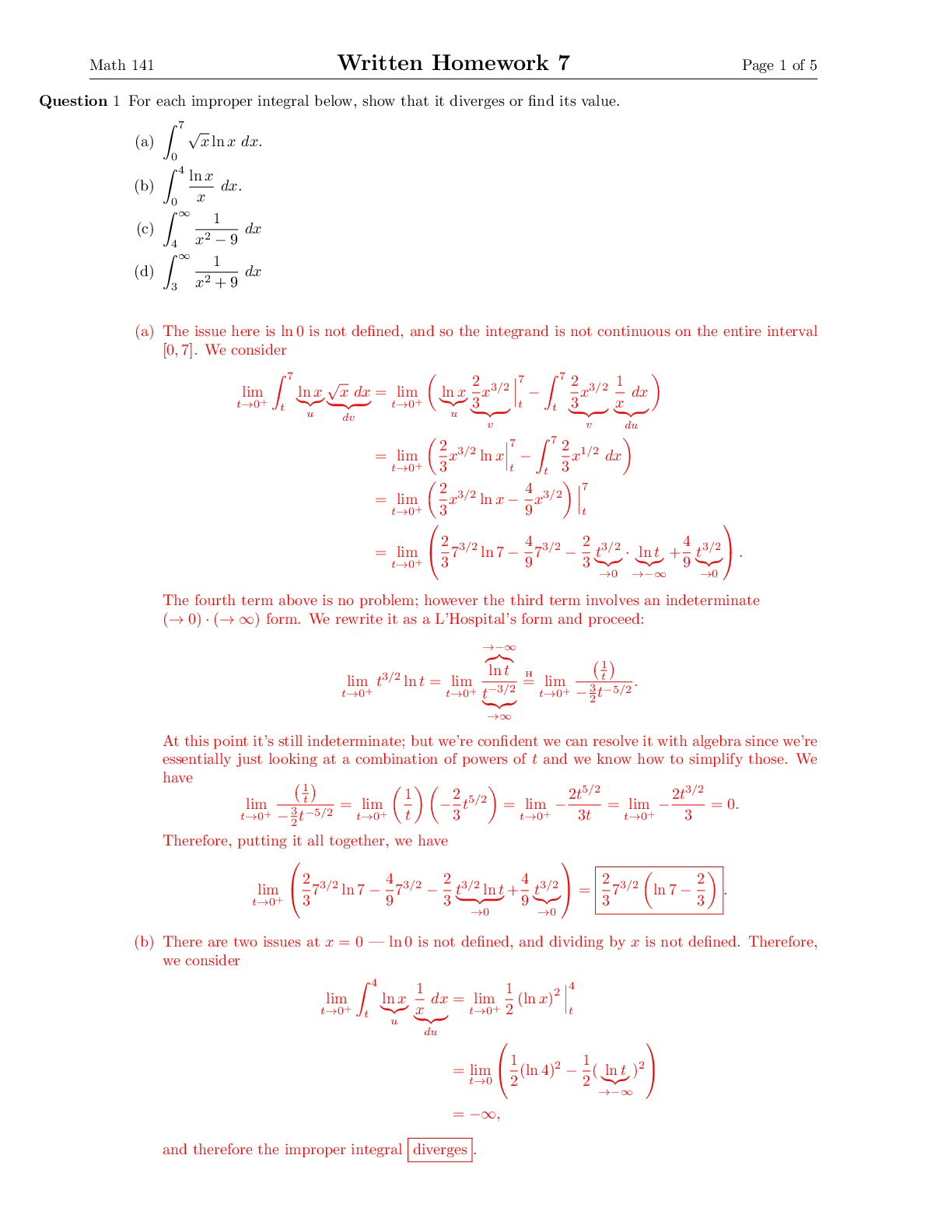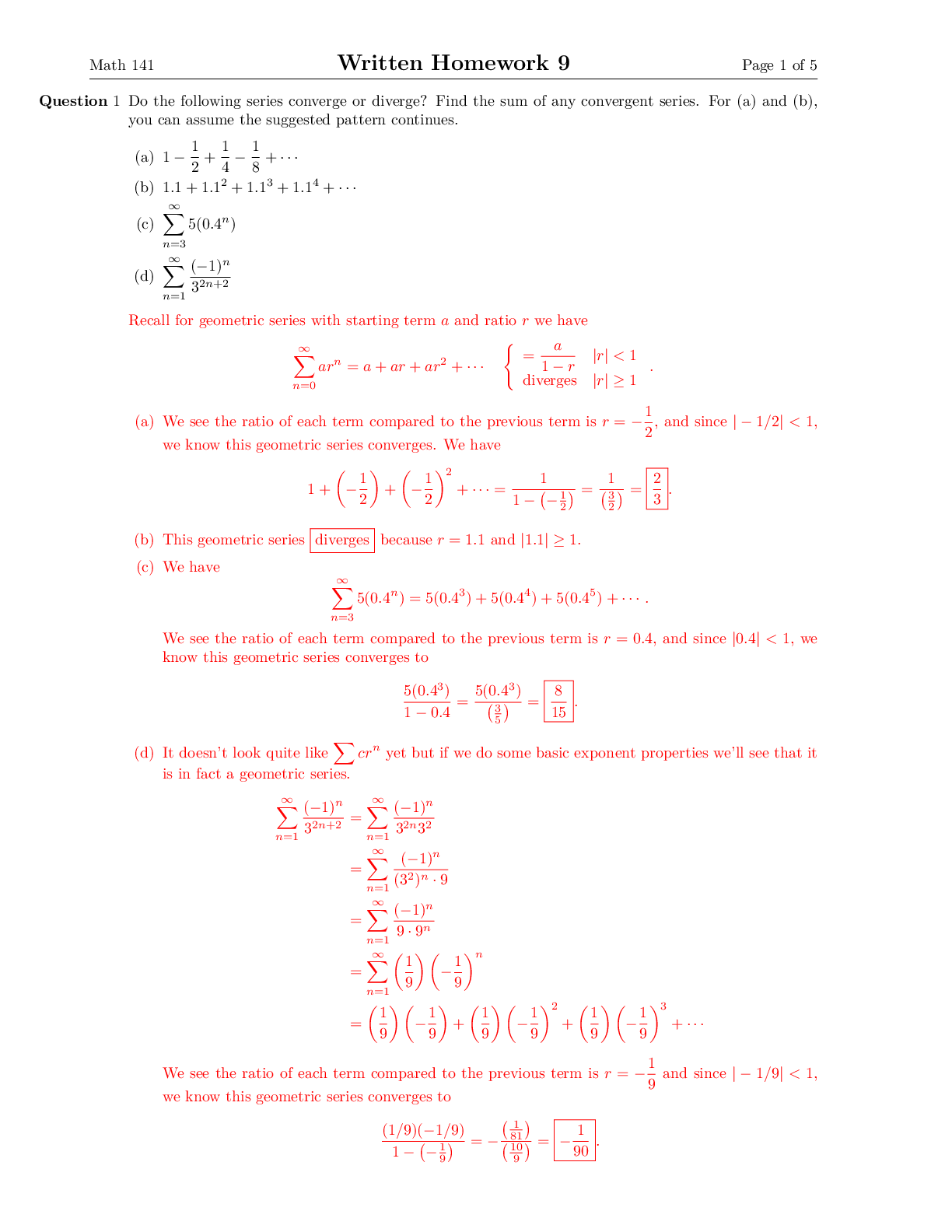Pennsylvania State University MATH 141 In-Class Worksheet Week 14 Solutions. Winter 2023

Document Content and Description Below

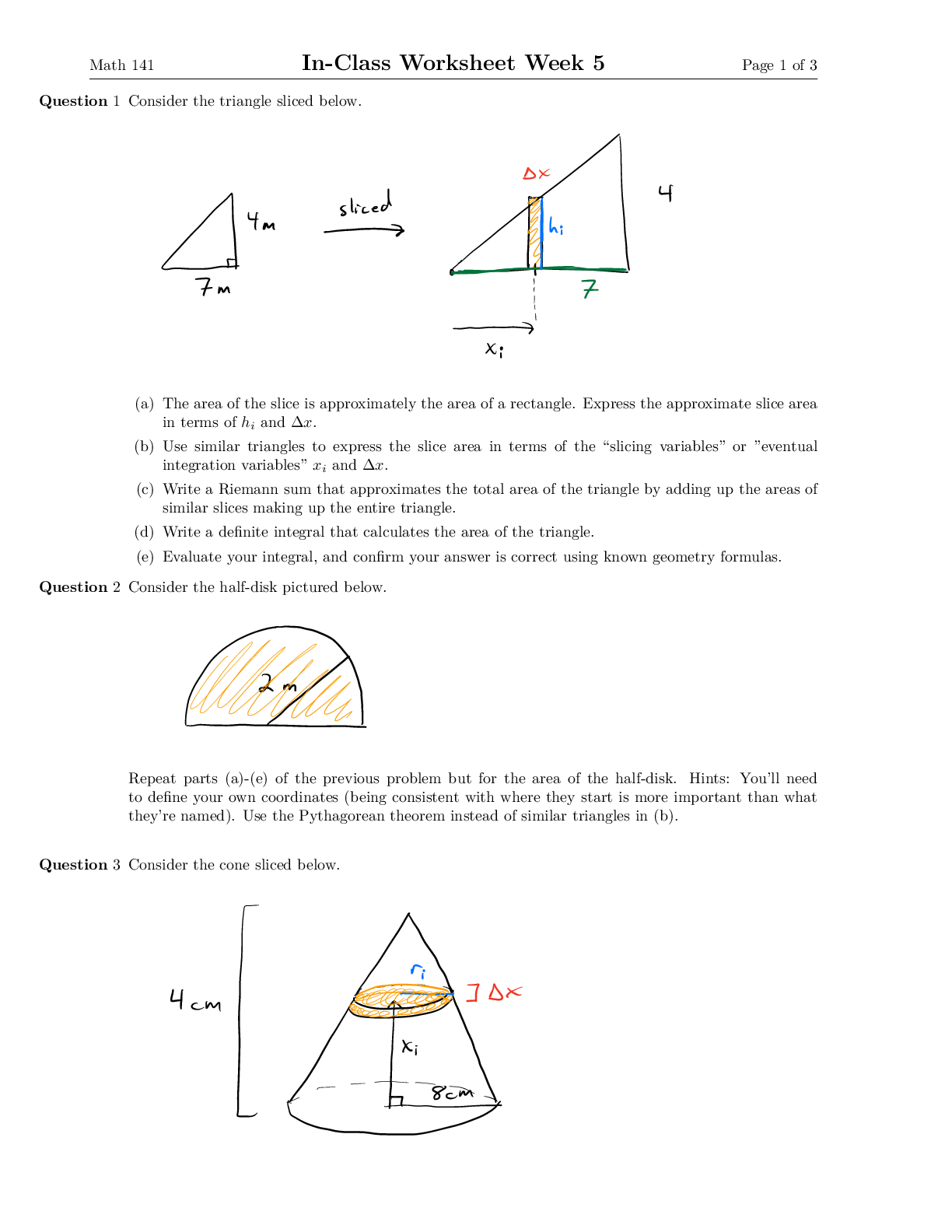
Math 141 In-Class Worksheet Week 14 Page 1 of 11 “Known” Maclaurin series expansions and the interval on which they’re valid: • ex = ∞ X n =0 xn n! , -∞ < x < ∞ • sin x =∞ X n... =0 (-1)nx 2n+1 (2n + 1)! - ∞ < x < ∞ • cos x =∞ X n =0 (-1)nx 2n (2n)! - ∞ < x < ∞ • tan-1 x = ∞ X n =0 (-1)nx2n+1 2n + 1 - 1 ≤ x ≤ 1 • ln(1 + x) = ∞ X n =1 (-1)n-1xn n - 1 < x ≤ 1 • (1 + x)p = 1 + px + p(p - 1) 2! x2 + p(p - 1)( 3! p - 2)x3 + · · · - 1 < x < 1 (this is true for more values of x for certain values of p) Question 1 Find the Maclaurin series of each of the following functions. Write the first three nonzero terms as well as the full series using summation notation. (a) h(x) = x3 cos(x3) (b) i(x) = Z x3 cos(x3) dx. Math 141 In-Class Worksheet Week 14 Page 2 of 11 Question 2 Write the first three nonzero terms (not counting the integration constant) of the Maclaurin series of Z √4 + 1 x2 dx. We have Question 3 Find the sum of each of the following series if they converge. (a) ∞ X n =0 (-1)nπ2n+1 42n+1(2n + 1)! (c) ∞ X n =0 (-1)n(√3)2n+1 2n + 1 Question 4 In statistics, the normal distribution with mean µ and standard deviation σ has the density function f(x) = e-(x-µ)2/2σ2 σ√2π . Math 141 In-Class Worksheet Week 14 Page 3 of 11 The normal distribution corresponds to the “bell curve” that you may have seen. For an example of how they are used, if the SAT score, x, of PSU applicants follows a normal distribution with mean µ and standard deviation σ, then Zab e-(xσ-√µ2)2π/2σ2 dx = the fraction of PSU applicants with SAT score between a and b. Unfortunately, we are unable to write antiderivatives of these types of density functions using our usual functions and combinations thereof, so historically this type of integral would be written into a “standard form”, after which you would consult a table of appropriate numerical values. The standard normal distribution has mean µ = 0 and standard deviation σ = 1, and has density function φ(x) = e√-x22π/2 . (a) Find the Maclaurin series for φ(x). Write out the first three nonzero terms as well as the full series using summation notation. (b) Use the first three nonzero terms from (a) to approximate Z-11 φ(x) dx. Math 141 In-Class Worksheet Week 14 Page 4 of 11 (c) You may have heard “In a normal distribution, about 68% of the values are within 1 standard deviation of the mean.” Confirm that your answer to (b) is consistent with this well known statistical fact. (For example, the worldwide SAT score distribution has mean 1060 and standard deviation 217, meaning that about 68% of test takers have scores between 1060 - 217 = 843 and 1060 + 217 = 1277.) Problems to work on throughout the last week of class: Question 5 For this problem consider the complex numbers z = 3 + 2i and w = 5 - i. For the following, give your answer in standard form a + bi, where a and b are real. (a) Calculate z + w. (b) Calculate z - w. (c) Calculate zw. (d) Calculate z w . Question 6 Consider the complex numbers z = 2eπ4 i and w = 4eπ2 i. (a) Use Euler’s identity separately for z and w, and then calculate zw. Give your answer in standard a + bi form. Math 141 In-Class Worksheet Week 14 Page 5 of 11 (b) Do the same calculation but first calculate zw while still in exponential form (using familiar exponential arithmetic), then use Euler’s identity on the result. Give your answer in standard a + bi form, making sure your answer agrees with (a). Question 7 Here we use Euler’s identity to derive the double angle identities for cosine and sine. On one hand, e2θi = cos(2θ) + i sin(2θ). On the other hand, e2θi = eiθ 2 = (cos θ+i sin θ)2 = cos2 θ+sin θ cos θ i+sin θ cos θ i+sin2 θ i2 = (cos2 θ-sin2 θ)+(2 sin θ cos θ) i. When written in standard form (a, b, c, d all real), a + bi = c + di guarantees both a = c and b = d, we have the familiar double angle identities cos(2θ) = cos2 θ - sin2 θ, sin(2θ) = 2 sin θ cos θ. Use similar reasoning to discover identities for cos(3θ) and sin(3θ). Question 8 Find polar coordinates (with 0 ≤ θ < 2π) for each of the following points in the xy-plane. Math 141 In-Class Worksheet Week 14 Page 6 of 11 (a) (1, 1) ait ti unify (b) (1, -1) ti ait ti (c) (-1, 1) Math 141 In-Class Worksheet Week 14 Page 7 of 11 (d) (-1, -1) . ait unify (e) (1, √3) ait ti unify (f) (-5√3, 5) Math 141 In-Class Worksheet Week 14 Page 8 of 11 unify Question 9 Express the following complex numbers in the form reiθ with 0 ≤ θ < 2π. (a) i 42.21 Éo 0 2 t É (b) -i 42.21 Éo 0 2 t É (c) 2 + 2i Math 141 In-Class Worksheet Week 14 Page 9 of 11 42.21 Éo 0 2 t É (d) 4 - 2√3 i t 42.21 Éo 0 2 t É Question 10 Provide inequalities for r and θ that precisely describe the following regions in the xy-plane. (a) the region bounded by the circle x2 + y2 = 9 Math 141 In-Class Worksheet Week 14 Page 10 of 11 . É (b) the region bounded by the circle x2 + y2 = 9 in the 2nd quadrant t 42.21 Éo 0 2 t É (c) the region in the first quadrant bounded by the x-axis, the line y = √x3, and the circle x2 +y2 = 2 t 42.21 Éo 0 2 t É (d) the triangular region with vertices (0, 0), (0, 1), and (1, 1) Hint: this can be done in polar coordinates, but rectangular coordinates are better suited. This example is so you learn that polar coordinates aren’t always the best choice. [Show More]

Last updated: 2 years ago

Preview 1 out of 11 pages