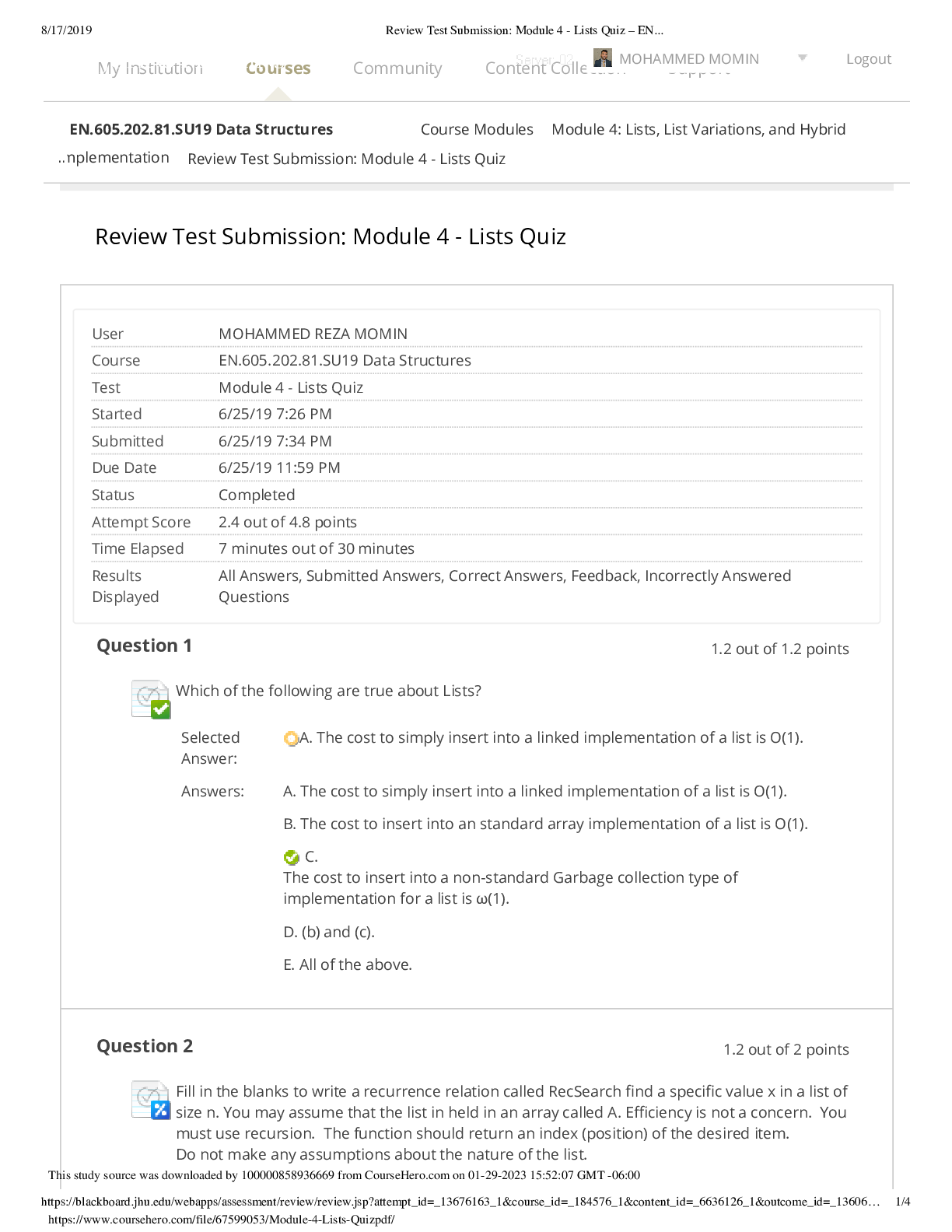
Physics > QUESTIONS & ANSWERS > Physics 104 Homework 1 Solutions Johns Hopkins University PHYSICS 171 (All)

Physics 104 Homework 1 Solutions Johns Hopkins University PHYSICS 171

Document Content and Description Below

Physics 104 Homework 1 Solutions Problem 1 (a) (i) In lecture we learned that the electric field due to a ring of charge along the axis of the ring of charge is entirely in the ˆz direction. The w... asher in the problem can be thought of as a series of concentric rings, where each ring contributes an electric field in the ˆz direction. This is because of the principal of superposition which says that electric field of a charge distribution is simply the sum of the electric fields of each particle in the distribution. Therefore, we expect the electric field of the washer should also be in the ˆz direction. (ii) Again the best way to think about the washer is as a series of rings. This is nice because we have already done the calculation for the electric field of a ring (no use doing more working than we have to). That is, Ez,ring = kQring z (z 2 + R2) 3/2 . (1) Notice that when z = 0, Ez,ring = 0. Hence, every ring in the washer contributes an electric field of zero. Therefore, the total electric field at z = 0 is Ez,ring = 0. (b) This problem can be done without integration, but let’s do it with integration so that we can better understand how the concentric rings make up the washer. To begin with, let’s find the charge within a single ring of the washer. If the ring has some area dA, then charge within this ring is given by dQ = σdA. If the ring has a radius r and thickness dr. The area of this ring is given by dA = 2πrdr. Hence, dQ = 2πσrdr. Now we want the total charge on the washer, so we need to sum up all of the rings of radii between a and b. This can be done with an integral given by: Qwasher = 2πσ Z b a rdr = σπ(b 2 − a 2 ). (2) Notice this is simply σ multipl [Show More]

Last updated: 2 years ago

Preview 1 out of 3 pages

Buy Now

Instant download

We Accept: