Mathematics > QUESTIONS & ANSWERS > MAT 2355 Introduction to Geometry - University of Ottawa- MAT2355 – INTRODUCTION TO GEOMETRY – S (All)

MAT 2355 Introduction to Geometry - University of Ottawa- MAT2355 – INTRODUCTION TO GEOMETRY – SECOND ASSIGNMENT. Complete Solutions.

Document Content and Description Below

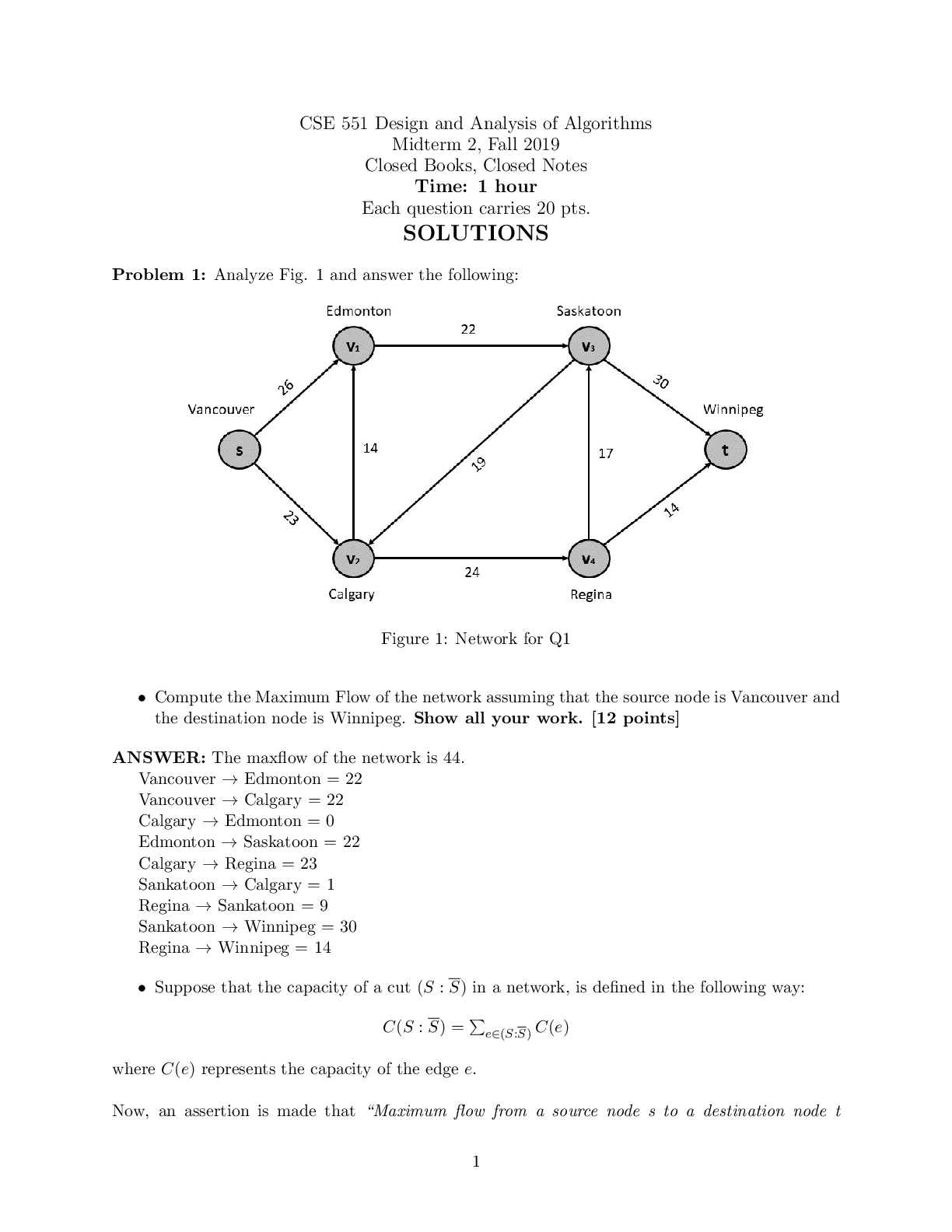
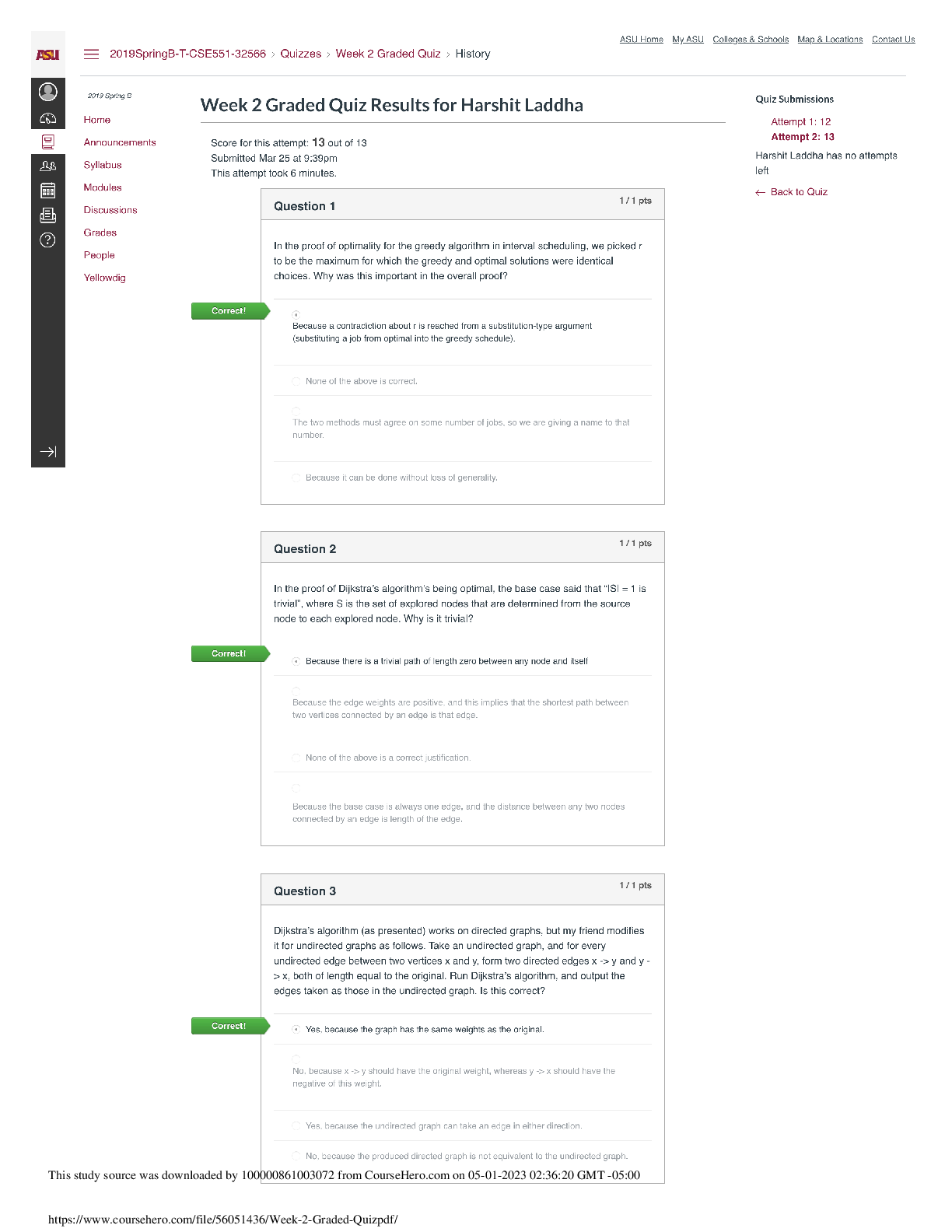
MAT2355 – INTRODUCTION TO GEOMETRY – SECOND ASSIGNMENT QUESTION 1. (a) (3 points) Compute a formula for the reflection R : E3 ! E3 by the plane z - 2y = -1. Your answer should determine the c... oordinates explicitly, i.e., it should be in the form R(x; y; z) = (· · · ; · · · ; · · · ) for every point (x; y; z) 2 E3. Solution: 2 (b) (2 points) Consider the map T : E3 ! E3 given by T (x; y; z) = (y; x; z). Find the equation of a plane H ⊂ E3 such that T is a reflection by H. You should justify that T is indeed a reflection by your plane H. Hint: To find the plane, use the fact that it is fixed by T . 3 (c) (2 points) Let S : E3 ! E3 be the map given by S(x; y; z) = (y; -z; -x). Prove that S is an isometry. Is S orientation-preserving or orientation-reversing? You should justify your answer. QUESTION 2. (4 points) For each of the following statements, determine if the statement is true or false. Circle T for the true statements and F for the false statements. For each correct answer you will receive 1 point. For each incorrect answer you will receive -1 points. If you do not circle any of the letters next to a statement, you will receive 0 points for that statement. T F For every reflection R‘ : E2 ! E2 by a line ‘ and every translation T~a : E2 ! E2 with displacement vector ~a we have R‘ ◦ T~a = T~a ◦ R‘. T F The composition of every two rotations of E2 is a rotation. T F If f : En ! En is an isometry, then f is one-to-one (that is, for every p1; p2 2 En if f(p1) = f(p2) then p1 = p2). T F If f; g : E2 ! E2 are two maps such that f and f ◦ g are isometries, then g is also an isometry. Grading Scheme: From top to bottom the answers are F, F, T, T. Give them 1 mark for each correct answer, -1 mark for each incorrect answer, 0 marks if there is no answer. The minimum mark for this question is 0 (that is, no negative marks). QUESTION 3. (2 points) Consider the line ‘ in the complex plane with equation z = (3 + i) + t(2 - 2i) ; t 2 R: Find the intersection of ‘ with the y-axis. You should give the point of intersection as a complex number. QUESTION 4. [3 points] You want to build a fence along a wall such that the area enclosed between the wall and the fence is 25 square meters. What is the minimum possible length of the fence, and its shape when the length is minimized? You should justify your answer. 5 Wall Fence 6 Q UESTION 5. (3 points) Let A; B; C be three points in the complex plane corresponding to the complex numbers a; b; c 2 C. Assume that jaj = jbj = jcj = 1. Also, let P be the point corresponding to a + b + c. Prove that the line through PA is perpendicular to BC. [Show More]

Last updated: 2 years ago

Preview 1 out of 6 pages

Buy Now

Instant download

We Accept: