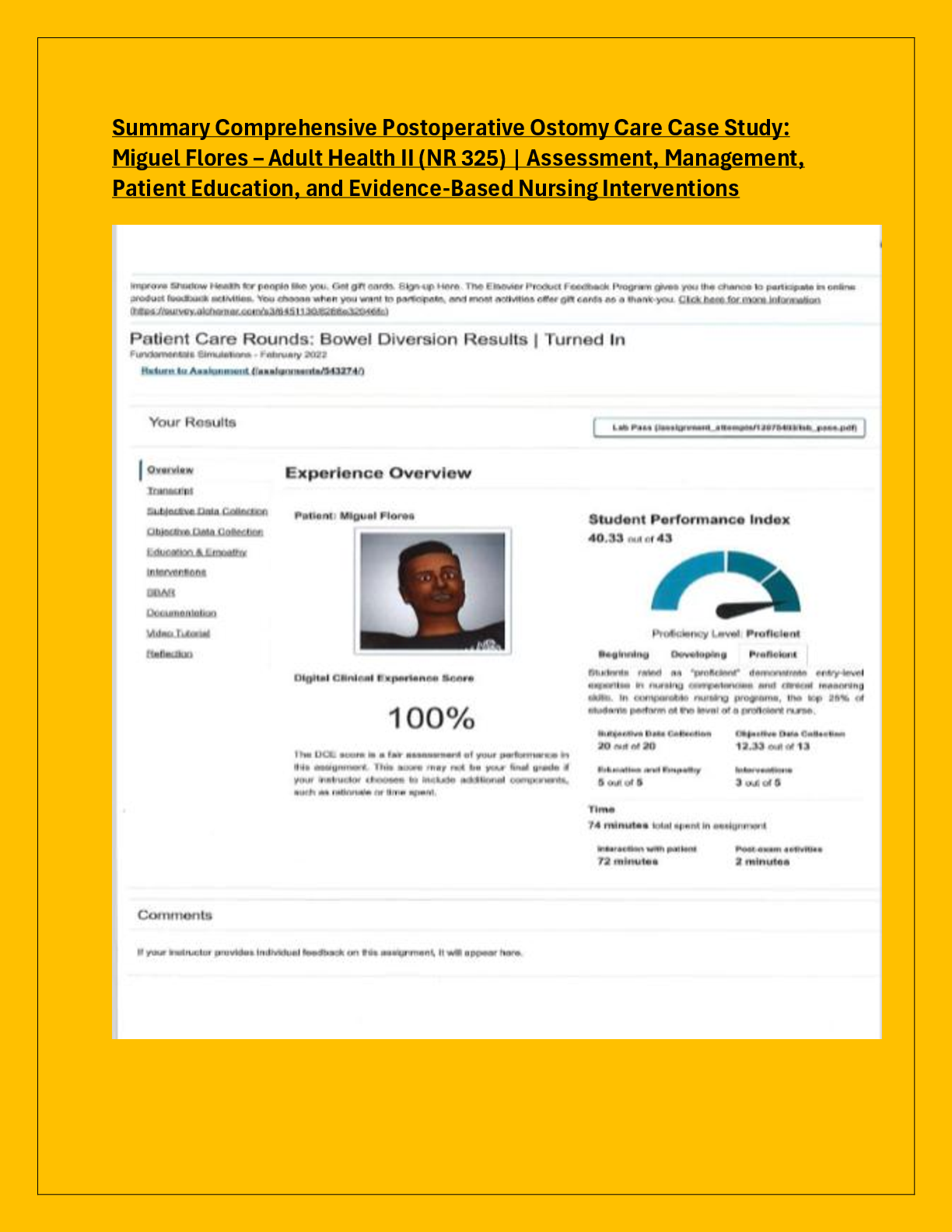
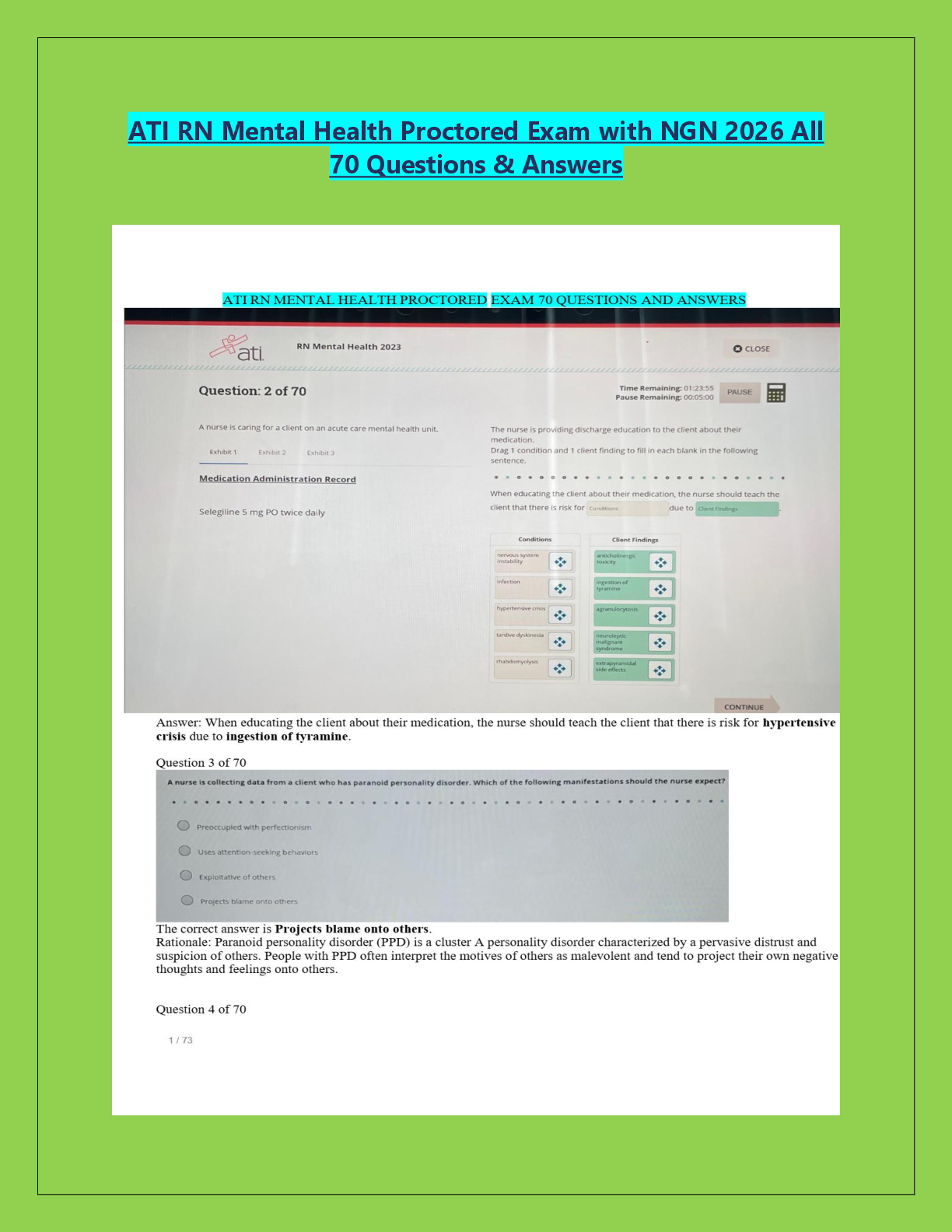
Statistics > EXAM > MATH 225N Week 6 Assignment 2020 - {Graded A} | Confidence Interval for Mean – Population Standard (All)

MATH 225N Week 6 Assignment 2020 - {Graded A} | Confidence Interval for Mean – Population Standard Deviation Known

Document Content and Description Below

MATH 225N Week 6 Assignment 2020 - Chamberlain College of Nursing | Confidence Interval for Mean – Population Standard Deviation Known Find the sample size required to estimate a population mean ... with a given confidence level Question The population standard deviation for the number of corn kernels on an ear of corn is 94 kernels. If we want to be 90%confident that the sample mean is within 17 kernels of the true population mean, what is the minimum sample size that should be taken? z0.101.282 z0.051.645 z0.0251.960. z0.012.326. z0.0052.576 Use the table above for the z-score. Correct! You nailed it. 21 83 329 699 Answer Explanation Correct answer: 83 The formula for sample size is n=z2σ2EBM2 In this formula, z=zα2=z0.05=1.645because the confidence level is 90%. From the problem, we know that σ=94 and EBM=17. Therefore, n=z2σ2EBM2=(1.645)2(94)2172≈82.74 Use n=83 to ensure that the sample size is large enough. Find the sample size required to estimate a population mean with a given confidence level Question Suppose the scores of a standardized test are normally distributed. If the population standard deviation is 2 points, what minimum sample size is needed to be 90% confident that the sample mean is within 1 point of the true population mean? z0.101.282z0.051.645z0.0251.960z0.012.326z0.0052.576 Use the table above for the z-score, and be sure to round up to the nearest integer. Yes that's right. Keep it up! 11 test scores Answer Explanation Correct answers: • 11 test scores The formula for sample size is n=z2σ2EBM2 In this formula, z=zα2=z0.05=1.645 because the confidence level is 90%. From the problem, we know that σ=2 and EBM=1. Therefore, n=z2σ2EBM2=(1.645)2(2)212≈10.82 Use n=11 to ensure that the sample size is large enough.Also, the sample size formula shown above is sometimes written using an alternate format of n=(zσE)2. In this formula, E is used to denote margin of error and the entire parentheses is raised to the exponent 2. Therefore, the margin of error for the mean can be denoted by "EBM" or by "E". Either formula for the sample size can be used and these formulas are considered as equivalent. Calculate and interpret the confidence interval for a population mean with a known standard deviation Question The length, in words, of the essays written for a contest are normally distributed with a population standard deviation of 442 words and an unknown population mean. If a random sample of 24 essays is taken and results in a sample mean of 1330 words, find a 99% confidence interval for the population mean. z0.10 z0.05 z0.025 z0.01 z0.005 1.282 1.645 1.960 2.326 2.576 You may use a calculator or the common z values above. •Round the final answer to two decimal places. Perfect. Your hard work is paying off ? (1097.59, 1562.41) Answer Explanation Correct answers: • (1097.59, 1562.41) Confidence intervals are written as - - - - - - -- - -- - Continued [Show More]

Last updated: 2 years ago

Preview 1 out of 14 pages

Buy Now

Instant download

We Accept: