Electrical Engineering > QUESTIONS & ANSWERS > Ohio State University - EE 421Continuous and Discrete Time Signals and Systems (Mandal &amp; Asi (All)

Ohio State University - EE 421Continuous and Discrete Time Signals and Systems (Mandal &amp; Asif) solutions - chap08

Document Content and Description Below

Chapter 8: Case Studies for CT Systems Problem 8.1: (a) The AM signal is given by s(t) = A[1+ 3k sin(2πf1t) + 2k cos(2πf2t)]cos(2πfct) . To ensure that the envelope of s(t) ≥ 0 for all t (1+... 3k sin(2πf1t) + 2k cos(2πf2t)) ≥ 0 . Taking the worst case scenario, i.e., both sin(2πf1t) and cos(2πf2t) take their minimum values of -1 at the same time, we get (1- 3k - 2k) ≥ 0 or, k ≤ 0.2 . (b) Expressing s(t) = Acos(2πfct) + [3k sin(2πf1t) + 2k cos(2πf2t)]cos(2πfct) , or, cos(2 ( ) ) cos(2 ( ) ). ( ) cos(2 ) sin(2 ( ) ) sin(2 ( ) ) 2 2 2 1 3 2 1 3 Ak f f t Ak f f t s t A f t f f t f f t c c c Ak c Ak c + π + + π - = π + π + + π - Assuming f1 ≠ f2 ≠ fc, the power in the modulated signal is composed of 2 12 Power in the carrier = A and 2 4 13 2 ( ) 2 (3 / 2) Power in the modulating signal 2 2 ( ) 2 2 = × Ak + × Ak = Ak . Hence, the ratio of power lost in the carrier and the total power = 2 1 6.5 1 + k . (c) The power spectrum of s(t) is given by [ ] [ ] [ ] [ ] [ ] ( 2 ( ) ( 2 ( ) . ( 2 ( ) ( 2 ( ) ( 2 ( ) ( 2 ( ) ( 2 ( ) ( 2 ( ) ( ) ( 2 ) ( 2 ) 2 2 2 2 2 1 1 3 2 1 1 3 Ak f f f f Ak f f f f j f f f f j f f f f S f A f f c c c c c c Ak c c Ak c c + π δ ω + π - + δ ω - π - + π δ ω + π + + δ ω - π + + δ ω + π - - δ ω - π - + δ ω + π + - δ ω - π + = π δ ω - π + δ ω + π π π For f1 = 10 kHz, f2 = 20 kHz, and fc= 50 kHz, the power spectrum is shown [Show More]

Last updated: 2 years ago

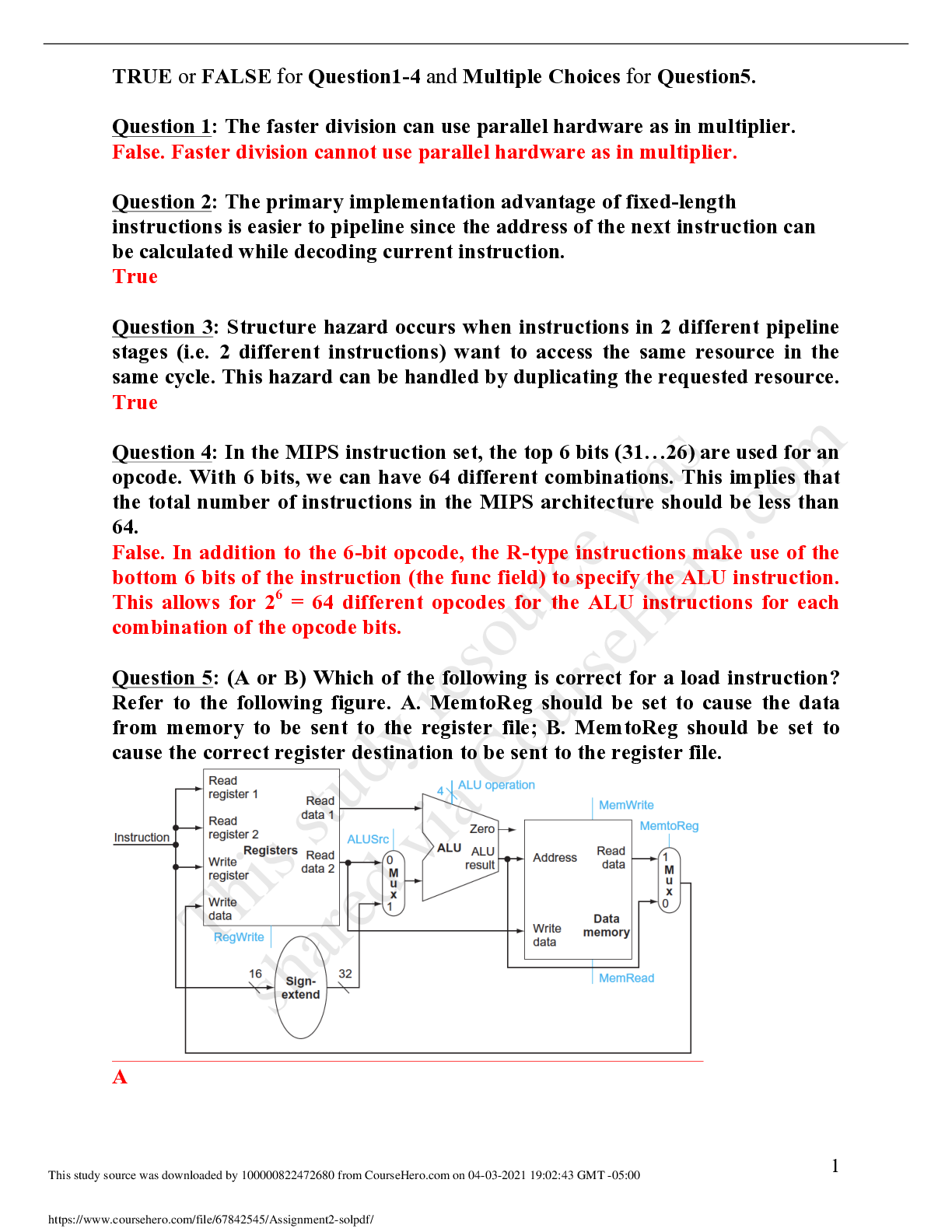
Preview 1 out of 9 pages

Buy Now

Instant download

We Accept: