PHYSICS 1111>Physics Lab 12 report<Simple Harmonic Motion-University Of Georgia(DRADED A)

Document Content and Description Below

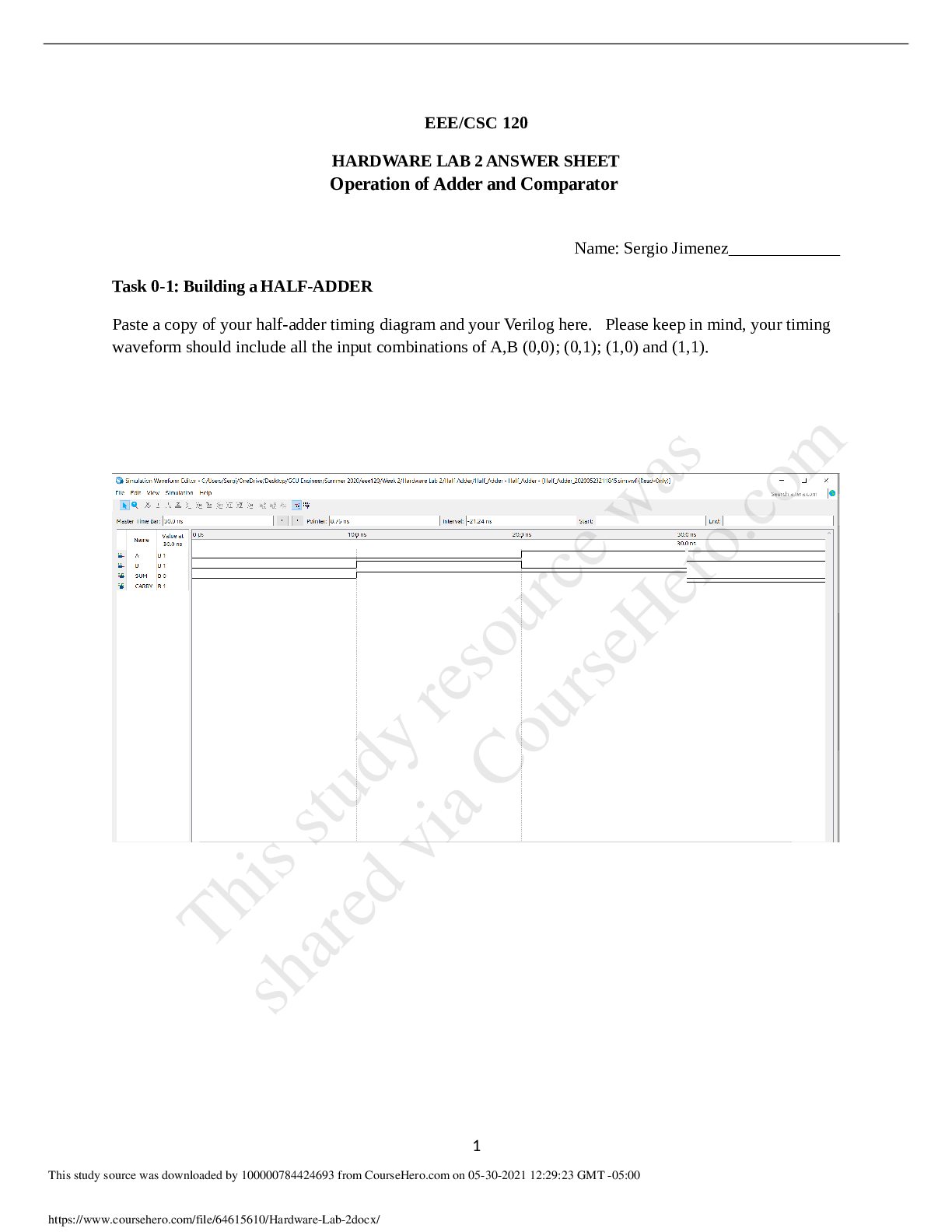
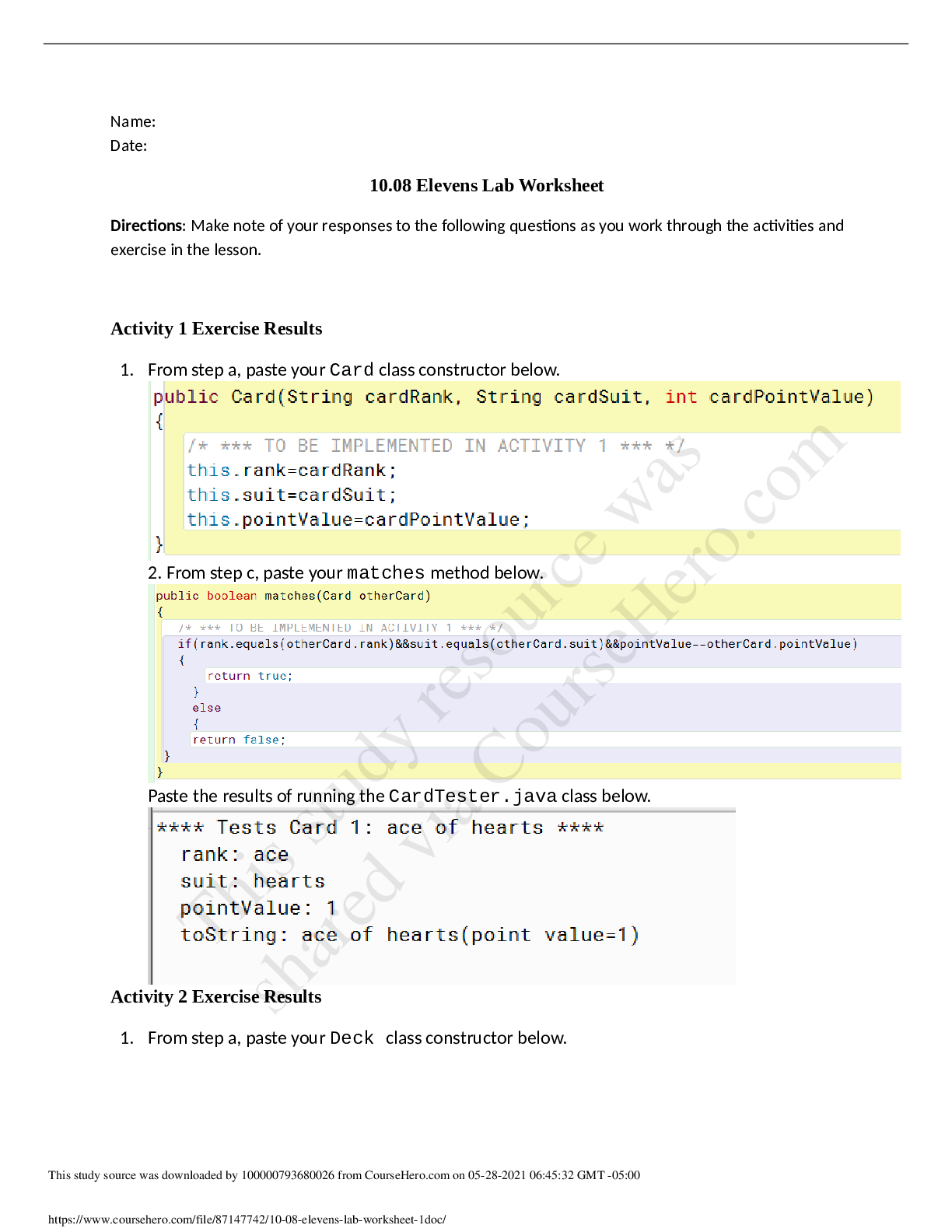
Learning Objectives: 1. Design an experiment to find an unknown quantity. 2. Use Hooke’s law to determine the spring constant of a spring. 3. Calculate and measure the period for an oscillating m ... ass and spring system. 4. Understand the dependence of period of a simple harmonic oscillator on the amplitude. Apparatus: Spring, metal stand and fixing bracket, mass hanger, set of weights, meter stick, stopwatch. Overview: In this experiment you will investigate simple harmonic motion for a spring and mass system. You will design an experiment to determine the spring constant of a given spring and use that to predict the period of oscillations. You will then measure the oscillation behavior of the spring and mass system. Part A: Finding the spring constant, k 1. The force exerted by a spring, Fsp , is always in a direction to restore the spring to its unstretched and uncompressed length. This is called a restoring force. An ideal spring is one where the magnitude of this spring force is directly proportional to how far the spring is stretched or compressed, d . This relationship is called Hooke’s Law and can be written as Fsp=kd . The constant, k , tells us the stiffness of the spring and is called the spring constant. We want to design an experiment to determine the spring constant k . A starting point may be to hang a mass from the spring as shown in the figure and to investigate the equilibrium of spring and mass system for this case. To develop your procedure, begin by drawing the free body diagram for the mass M. Then use the forces on your diagram to write down Newton’s Second Law in the vertical direction. Also write down’s Hooke’s Law for the force from a spring. 2. Now use Newton’s Second Law and Hooke’s Law to come up with an experiment that will allow you to determine the unknown spring constant from quantities you can measure. Describe your experimental design by answering the three questions below. What will you do? I will set up my experiment by using a spring, whose length is known, and then attach a mass M, the mass will change. The spring will be attached to a block or stand at the top so it is in a fixed position, and then different masses will be added in order to see how much the spring is stretched. 1 This study source was downloaded by 100000793680026 from CourseHero.com on 04-20-2021 18:01:51 GMT -05:00 https://www.coursehero.com/file/86740570/Physics-Lab-12docx/ This study resource was shared via CourseHero.comWhat data will you collect? I will be collected the mass (M), since that value will change. I will also collect the distance (d) the spring has stretched in correspondence to each mass. Since we have the mass we can find the downward force (F) by multiplying the mass to g. How you will analyze the data? By using both Newton’s Second Law and Hooke’s Law we can derive the equation k=Mg/d. By using the data we collected we can insert those values into the equation and find the value of k. 3. Now label the axes of the graph you plan to construct and sketch your prediction of the data you will get. Next to your predicted graph, show how you will determine the spring constant from the data. 4. Now you are ready to do the experiment to determine the spring constant. Go to the following web page and launch the simulation: https://phet.colorado.edu/sims/html/masses-and-springs/latest/masses-and-springs_en.html Starting on the Tab labeled Intro, you will find two identical springs, an assortment of masses, and a ruler. You also have several options to display reference lines. Think about how you will establish your point of reference to measure any required lengths. The stop sign will allow you to stop the mass from oscillating. Make a table below and enter your data. Make sure to put labels on each column with units. 2 Mass (kg) Displacement (m) Force (N) 0.000 0.00 0 0.050 0.08 0.49 0.100 0.17 0.98 0.250 0.41 2.45 5. Now construct a graph of your data that you can use to determine k . Remember units. You can make the graph below or use Excel and paste the graph below. In either case, make sure to title your graph and label your axes. 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0 0.5 1 1.5 2 2.5 3 f(x) = 5.96 x − 0 Force vs Mass Displacement (kg) Force (N) . Calculated Spring Constant: k = 5.96N/m Part B: Simple harmonic motion 7. The period of an oscillation is the time required for one complete cycle. For an ideal spring-mass system the period, T , of oscillations is predicted to be T=2 π√mk , where m is the mass suspended from the spring. Predict the period of the oscillation you will get if you attach a mass of 100 g to the spring. Use 3 This study source was downloaded by 100000793680026 from CourseHero.com on 04-20-2021 18:01:51 GMT -05:00 https://www.coursehero.com/file/86740570/Physics-Lab-12docx/ This study resource was shared via Cou [Show More]

Last updated: 3 years ago

Preview 1 out of 7 pages