BR 2201Solution John_E_Freunds_Mathematical_Statistics_with_ApplicationsREVIEWED BY EXPERTS-2021

Document Content and Description Below

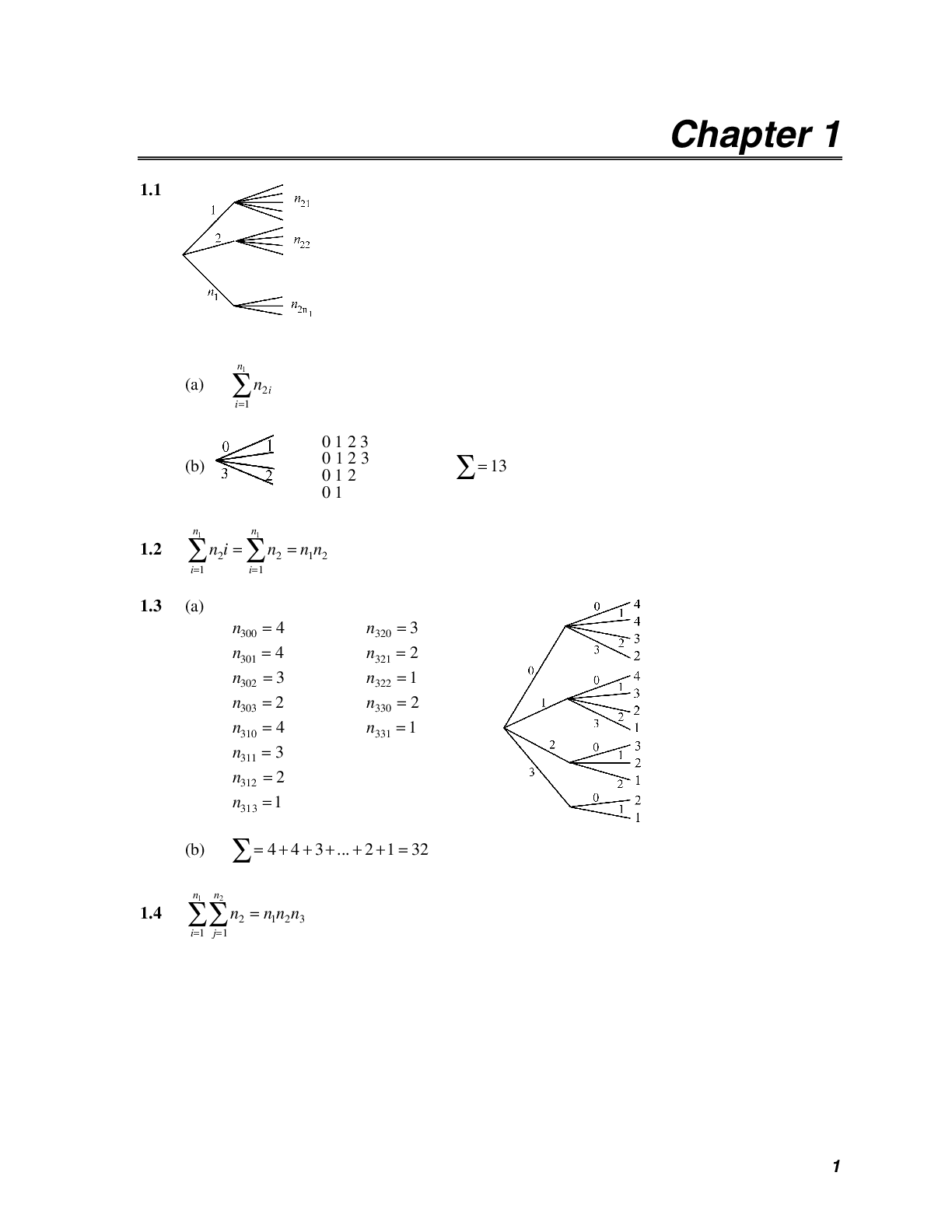
Chapter 1 1.1 (a) 1 2 1 n i i n  (b) 0 1 2 3 0 1 2 3 0 1 2 0 1  13 1.2 1 1 2 2 1 2 1 1 n n i i n i n n n      1.3 (a) n300  4 n320  3 n3... 01  4 n321  2 n302  3 n322  1 n303  2 n330  2 n310  4 n331  1 n311  3 n312  2 n313  1 (b)  4  4  3...  2 1  32 1.4 1 2 2 1 2 3 1 1 n n i j n n n n    2 Mathematical Statistics, 8E 1.5 (b) 6, 20, and 70 “2 out of 3” m = 2 1 2 2 2(1 2) 6 1 1                   “3 out of 5” m = 3 2 3 4 2 2(1 3 6) 20 2 2 2                           “4 out of 7” m = 4 3 4 5 6 2 2(1 4 10 20) 70 3 3 3 3                                   1.6 (a) 10 10 10 10! 0 (7.92665)(3.678797) (7.92665)(454,002.49) 3,598,719 e   π         % error 3.6288 3.5987 100 0.83% 3.6288     12 12 12 12! 24 (8.683215)(4.41455) 475,683,224 e  π        4.7800 4.7568 % error 100 0.69% 4.7900     (b) 52 13 39 52 52 52 13 39 39 39 52 104 52 52! 13 13! 39! 13 39 26 78 13 4 4 639 billion 19.5 13 13 3 19.5 3 e e e π π π π π                               1.7 Using Stirling’s formula in 2 2 ! ! ! n n n n n        yields 2 2 2 2 2 2 4 1 2 2 2 n n n n n n n n n e n n e π π π π π                              1.8 nr and 123 = 1,728 1.9 1 5 3 1 7 and 21 5 5 r n r                         1.10 Substitute r  n for r into result of 1.9 1 1 5 1 4 and 6 5 3 2 r n n r r n r n                                   Chapter 1 3 1.11 (b) Seventh row is 1, 6, 15, 20, 15, 6, 1 Eighth row is 1, 7, 21, 35, 35, 21, 7, 1 (x  y)6  x6  6x5y 15x4 y2  20x2 y3 15x2 y4  6xy5  y6 (x  y)7  x7  7x6 y  21x5 y2  35x4 y3  35x3y 4  21x2 y5  7xy6  y7 1.14 (a) Set x = 1 and y = 1 (b) Set x = 1 and y = 1 (c) Set x = 1 and y = a  1 1.19 (a) 1 1 3 5 2 2 2 2 15 24 384                     and ( 3)( 4)( 5) 10 6      (b) 1 2 1 5 2 1 4         2 3 1 1 1 1 1 1 1 3 1 2 1 2 4 2 2 4 2 2 2 4 1 1 3 512 64 8 3 2 1 2 8 64 512 512 571 2 2.23 512                                                               1142 2.230 512  1.20 (a) ( 1)( 2)...( ) ( 1) ! r r r      (b) ( )( 1)...( 1) ( 1) ( 1)...( 1) ! ! ( 1)...( 1) 1 ( 1) ( 1) ! r r r n n n n r n n n r r r r n r n n n r r r                                  1.21 8! 8 7 6 5 4 560 2! 3! 3! 2 6        1.22 9! 23 32 ( 4)3 9 8 7 6 5 4 8 9 64 23,224,320 3! 2! 3! 12               4 Mathematical Statistics, 8E 1.24 Note: If there are 0 turn-ons the first night, 6 turn-ons in four nights can only occur if there are 2 turn-ons on each of the subsequent three nights. Thus, we need to show only that part of the tree following this event.Chapter 1 5 1.25 1.26 (a) (b) 1.27 (a) 5 (b) 4 1.28 1.29 1.30 (a) 65  30; (b) 66  36; 1.31 (a) 6; (b) 65  30; (c) 5 4  20 first one fixed; (d) 6  30  20  566 Mathematical Statistics, 8E 1.32 (a) 45 2  40; (b) 5 63  90 1.33 (a) 5 4  20; (b) 5 4 3  60 1.34 315  14,348,907 1.35 15 14 105 2 1    1.36 (a) 1098 7  5040; (b) 5040 210 24  1.37 (a) 14 13 91; 2 1    (b) 14 13 12 364 3 2 1      1.38 6!  720 1.39 6! 720 90 2! 2! 2! 8   1.40 5!  120 and 120  2 4!  72 1.41 7!  5040 1.42 (a) 5!  120; (b) 5! 60 2!  1.43 10! 3628800 50,400 3! 3! 2! 72   and 8! 40320 3360 3! 2! 12   1.44 10! 3628800 1,260 5! 4! 120 24    1.45 8! 40320 280 3! 4! 6 24    1.46 (a) 20 77,520 7        ; (b) 20 184,755 10        (c) 20 20 20 20 1140 190 20 1 1351 17 18 19 20                                 1.47 (a) 7 21 2        ; (b) 4 6 2        ; (c) 3 4  12Chapter 1 7 1.48 3 7 3 7 3 21 1 7 63 7 70 2 2 3 1                                 1.49 4 7 3 6 35 3 630 2 3 1                       1.50 13 13 13 13 1287 286 286 78 8,211,173,256 5 3 3 2                              1.51 7! 5040 420 3! 2! 12   1.52 310  59,049 1.53 55  15,625 1.54 12 6 1 17 17 6,188 12 12 5                        1.55 12 1 11 462 6 6                1.56 14 3 1 16 120 14 14                 1.57 2 1 1 1 1 r n n r n n n                     1 10 45 1 2 r n  n                8 ScholarStock Chapter 2 2.1 (a) P[A]  P[( A B)  ( A B)]  P( A B)  P( A B)  P( A B) (b) A B  ( A B)  ( A B)  ( A  B)  A (A  B) 2.6 P(A)  P( A B)  (a  b)  a  b  P( A B) P(A B)  P( A)  P(A  B)  P( A) 2.7 1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) P A P B P A B a b c d a b a c a d P A B                   2.8 [( ) ( )] ( ) ) 2 ( ) ( ) 2 ( ) Refer to Figure 2.6 P A B A B b c a b a c a P A P B P A B                 2.9 (a) P(A)  P(B)  P(A B)  0  P(A B)  P(A)  P(B) (b) P(A)  P(B)  P(A B)  1 ( P A B)  P(A)  P(B) 1 2.10 Refer to Figure 2.7 P(A)  1  e  c  f  0 P(B)  1  d  f  g  0 P(C)  1  b  e  g  0 Therefore P(A)  a  b  d  g  a  1 QED 2.11 ( ) ( ) [ ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) QED P A B P A P A B P A P A B P A B P A B P A P B P A B                  2.12 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ( ) ( ) ( ) ( ) ( ) ( ) P A P B P C P A B P A C P B C P A B C a b d g a b c e a c d f a b a d a c a a b c d e f P A B C D                                        Chapter 2 9 ScholarStock 2.13 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) P A P B P C P D P A B P A C P A D P B C P B D P C D P A B C P A B D P A C D P B C D P A B C D                                ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) a b d g i j l o a b c e i j k m a c d f i k l n a b c d e f g h a b i j a d i l a b d g a c i k a b c e a c d f a i a b a d a c a a b c d e f g h i j k l m n o P                                                                                  ( A B  C  D) 2.14 For n  2, P(E1  E2)  P(E1)  P(E2)  P(E1  E2)  P(E1)  P(E2) Assume that for some n : 1 2 1 ( ) ( ) n n j j P E E E P E       , then  1 2 1  1 2 1 1 1 2 1 ( ) 1 ( ) ( ) ( ) ( ) j n n n n n n n P E j P E E E E P E E E E P E E E P E                         where the first inequality follows from the first step of the induction, and the second inequality comes from the second step of the induction. 2.15 1 p A p B   , pb  A Ap , PA pB  A, p( A B)  A , p A A B   2.16 (a) P:ostulate 1 P(A) a 0 a b    (B) Postulate 2 P(A) a a b   , P(A ) b a b    P(A) P(A ) a b 1 P(S) a b a b         2.17 (a) ( ) ( ) 0; ( ) P A B P A B P B    (b) ( ) ( ) ( ) 1 ( ) ( ) P B B P B P B B P B P B     (c) 1 2 1 2 1 2 1 2 [ ) ] ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) P A A B P A A B P B P A B P A B P B P B P A B P A B                  10 Mathematical Statistics, 8E ScholarStock 2.18 For example (a) If P(A B)  P( A B)  P( A  B) 1 ( ) 4  P A  B  so that 1 ( ) , 2 P B A  ( ) 1 , 2 P B A  and P(B A)  P(B A)  1 (b) If ( ) ( ) ( ) 1 5 P A B  P A B  P A  B  and ( ) 2 5 P A  B  1 ( ) , 2 P B A  ( ) 1 , 3 P B A  and 5 ( ) ( ) 6 P B A  P B A  2.19 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) P A B C D P A B C P D A B C P A B P C A B P D A B C P A P B A P C A B P D A B C                  2.20 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) P A B C P B C P A B C P A B P C A B P C B P A B P B P B C P B P A B C P A B                  2.21 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) P A B P A B P B A P B P A P A B P A P A P B         2.22 (a) P(B)  P(A B)  P(A  B)  P(A)P(B)  P( A  B) P(A  B)  P(B)  P( A)P(B)  P(B)[(1 P( A)]  P(B)P( A) QED (b) P(B)  P(A B)  P( A  B)  P(A  B)  P(B)P( A) P(A  B)  P(B)  P(B)P( A B)  P(B)[(1 P(A)]  P(B)P(A) QED 2.23 Assume that A and B are independent and show that this leads to contradiction. P(A)  P(A B)  P(A B)  P(A B)  P(A)P(B) P(A B)  P( A)  P( A)P(B)  P( A)[1 P(B)]  P( A)P(B) and A and B are independent 2.24 P(A)  0.60, ( P B)  0.80, ( P C)  0.50, ( P A B)  0.48, ( P AC)  0.30 P(B C)  0.38, ( P A B C)  0.24 P(A B C)  0.24, ( P A)(B)(C)  (0.6)(0.8)(0.5)  0.24 P(B C)  0.38, ( P B)P(C)  (0.8)(0.5)  0.40 B and C not independentChapter 2 11 ScholarStock 2.25 Refer to 2.21 ( P A B)  0.48, ( P A)P(B)  (0.6)(0.8)  0.48 A and B independent ( P AC)  0.30, ( P A)P(C)  (0.6)(0.5)  0.30 A and C independent ( P B C)  0.38, ( P B)P(C)  (0.8)(0.5)  0.40 B and C not independent 2.26 (Refer to 2.24 and 2.25) Already showed that A and B independent,. A and C independent P[( A(B C)]  0.54, ( P A)  0.60, ( P B C)  0.92, (0.6)(0.92)  0.552  0.54 2.27 (a) P[( A(B C)]  P( A B C)  P( A)P(B)P(C)  P(A)P(B C) QED (b) [( ( )] [( ) ( )] ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ( ) ( ) ( )] ( ) ( ) QED P A B C P A B A C P A B P A C P A B C P A P B P A P C P A P B P C P A P B P C P B C P A P B C                       2.28 ( ) ( ) ( ) ( ) ( ) ( ) P A B P A B P B P B A P B P A      2.29 Proof by induction: If n = 2, then P(A1  A2)  P( A1)  P( A2)  P( A1) P( A2) and 1[1 P( A1)][1 P( A2)]  11 P(A1)  P( A2)  P( A1)P( A2). Assuming P(A1  A2   An )  1[1 P( A1)][1 P( A2)] [1 P( An )]. we can write 1 2 1 1 2 1 1 2 1 1 2 1 1 ( ) ( ) ( ) ( ) ( ) ( ) [1 ( )] ( ) n n n n n n n n n P A A A A P A A A P A P A A A P A P A A A P A P A                              1 2 1 1 1 2 1 {1 [ ( )] [1 ( )] [1 ( )]} [1 ( )] ( ) 1 [1 ( )] [1 ( )] [1 ( )] [1 ( )] n n n n n P A P A P A P A P A P A P A P A P A                          2.30 Two at time k 2       Three at time k 3       k at time k k       2 2 1 2 3 0 1 k k k k k k k k k                                        2.31 P(A)  P( A) P( A)  P(A) P(), since ( P  A)  P()  0.12 Mathematical Statistics, 8E ScholarStock 2.32 Since B1  B2   Bk  S, A (B1  B2   Bk )  A. Thus, by the distributive property, ( A B1) ( A B2)   ( A Bk )  A , and P(A)  P(B1)P(A B1)  P(B2)P(A B2)   P(Bk )P( A Bk ) QED 2.33 The probability of no matches on any given trial is n 1  n ; since the trials are independent, the probability of no match in n trials is n 1 n 1 1 n n n                . 2.34 ( ) ( ) ( ) ( ) [1 ( )] [1 ( )] ( ) 1 ( ) ( ) [1 ( )]. P A B P A P B P A B P A P B P A B P A P B P A B                      Since 1 P( A B)  0, ( P A B)  1 P( A)  P(B) QED 2.35 (a) {6, 8, 9}; (b) {8}; (c) {1, 2, 3, 4, 5, 8}; (d) {1, 5}; (e) (2, 4, 8}; (f)  2.36 (a) Los Angeles, Long Beach, Pasadena, Anaheim, Santa Maria, Westwood; (b) San Diego, Long Beach, Pasadena, Anaheim, Santa Maria, Westwood; (c) Santa Barbara; (d) ; (e) San Diego, Long Beach, Santa Barbara, Anaheim; (f) San Diego, Santa Barbara, Long Beach; (g) Los Angeles, Santa Barbara, Anaheim; (h) Los Angeles, Pasadena, Santa Maria, Westwood; (i) Los Angeles, Pasadena, Santa Maria, Westwood. 2.37 (a) {5, 6, 7, 8}; (b) {2, 4, 5, 7}; (c) {1, 8} (d) (3, 4, 7, 8} 2.38 (a) He chooses a car with air conditioning. (b) He chooses a car with bucket seats or no power steering. (c) He chooses a car with bucket seats that is 2 or 3 years old. (d) He chooses a car with bucket seats that is 2 or 3 years old. 2.39 (a) House has fewer than three baths; (b) does not have fire place; (c) does not cost more than $200,000 (d) is not new; (e) has three or more baths and fire place; (f) has three more baths and costs more than $200,000 (g) costs more than $200,000 but has no fire place; (h) is new or costs more than $200,000 (i) is new or costs $200,000 or less (j) has 3 or more baths and/or fire place; (k) has 3 or more baths and/or costs more than $200,000; (l) is new and costs more than $200,000Chapter 2 13 ScholarStock 2.41 (a) (H,1), (H,2), (H,3), (H,4), (H,5), (H,6) (T,H,H), (T,H,T), (T,T,H), (T,T,T) (b) (H,1), (H,2), (H,3), (H,4), (H,5), (H,6), (T,H,T), (T,T,H) (c) (H,5), (H,6), (T,H,T), (T,T,H), (T,T,T) 2.42 (a) S = {(0,0,0)(1,1,1)} A = {(1,0,1),(0,1,1),(1,1,1)} B = {(0,1,1)} C = {(1,0,1)} (b) A & B not mutually exclusive, A & C not mutually exclusive, B & C are mutually exclusive. 2.43 3, 3, 3, 3, x1 x1x2 x1x2x3  where x1  1,2,4,5,6, for all i (a) 5k1; (b) 1 5 5 5 1 4 k k     2.44 S  {(x, y) (x  2)2  ( y  3)2  9} 2.45 (a) (x 3  x  10) ; (b) (x 5  x  8) ; (c) (x 3  x  5); (d) (x 0  x  3 or 5  x  10) 2.46 1 A driver has liability insurance and collision insurance. 2 A driver has liability insurance but not collision insurance. 3 A driver has collision insurance but not liability insurance. 4 A driver has neither liability insurance nor collision insurance. 2.47 (a) A driver has liability insurance. (b) A driver does not have collision insurance. (c) A driver has either liability or collision insurance, but not both. (d) A driver does not have both kinds of insurance. 2.48 (a) A car brought to the garage needs engine overhaul, transmission repairs, and new tires. (b) A car brought to the garage needs transmission repairs, new tires, but no engine overhaul. (c) A car brought to the garage needs engine overhaul, but neither transmission repairs nor new tires. (d) A car brought to the garage needs engine overhaul and new tires. (e) A car brought to the garage needs transmission repairs, but no new tires. (f) A car brought to the garage does not need engine overhaul. 2.49 (a) 5; (b) 1 and 2 together (c) 3, 5, and 6 together; (d) 1, 3, 4, and 6 together14 Mathematical Statistics, 8E ScholarStock 2.50 500  (308 266) 103  29  59 results are inconsistent 2.51 200  (1.38 115)  91  38 2.52 (a) 12; (b) 6; (c) 20 2.53 (a) permissible; (b) not permissible because the sum of the probabilities exceeds 1; (c) permissible; (d) not permissible because P(E) is negative (e) not permissible because the sum of the probabilities is less than 1. 2.54 (a) 1 0.37  0.63; (b) 1 0.44  0.56 ; (c) 0.37  0.44  0.81; (d) 0; (e) 0.37, P(A B)  P(A) for mutually exclusive events; (f) 1 0.81  0.19 2.55 (a) Probability cannot be negative. (b) 0.77  0.08  0.85  0.95 (c) 0.12  0.25 0.36  0.14  0.09  0.07  1.03  1 (d) 0.08 0.21 0.29  0.40  0.98  1 2.56 (a) 0.12  0.17  0.29; (b) 0.17  0.34  0.29  0.80 (c) 0.34  0.17  0.12  0.63; (d) 0.34  0.29  0.08  0.71Chapter 2 15 ScholarStock 2.57 (0,0), (1,0), (2,0), (3,0), (4,0), (5,0), (0,1), (1,1), (2,1), (3,1), (4,1), (5,1), (0,2), (1,2), (2,2), (3,2), (4,2), (5,2), (0,3), (1,3), (2,3), (3,3), (4,3), (5,3), (0,4), (1,4), (2,4), (3,4), (4,4), (5,4) (a) 10 1 ; 30 3  (b) 5 1 ; 30 6  (c) 15 1 ; 30 2  (d) 10 1 30 3  2.58 (a) 20 10 3; 4 5 1 80 8 80 4     ; (c) 2 4 1 ; 80 10   (d) 4 2 1 1 1 ; 80 10     (e) 8 14 22 11 80 80 40    2.59 (a) 0.24  0.22  0.46; (b) 0.15 0.03 0.22  0.40 (c) 0.03 0.08  0.11; (d) 0.15 0.03 0.28 0.22  0.68 2.60 16 2 120 20 52 1326 221 2               2.61 Let P(A)  4 p, ( P B)  2 p, ( P C)  2 p, and ( P D)  p . Then 9 p  1 and 1 9 p  ; (a) 2 ; 9 (b) 1 4 5 9 9   2.62 (a) 13 4 4 44 2 2 2 13 12 6 6 44 120 198 0.0475 52 2 52 51 50 49 48 4165 5                                      (b) 13 48 13 48 120 1 52 51 51 50 49 48 4165  5              16 Mathematical Statistics, 8E ScholarStock 2.63 (a) 5 6 5 3 4 2 2 2 15 10 3 4 25 6 6 6 6 6 6 108                             (b) 5 5 6 5 4 3 6 10 5 4 25 4 25 6 6 6 6 6 6 648 162                    (c) 5 5 2 6 5 3 2 6 5 10 25 6 6 6 6 6 6 648                      (d) 5 5 6 5 4 6 5 5 25 6 6 6 6 6 6 1296                2.65 78 [64 36 34] 12 2 78 78 13      2.64 (a) P(A B) is less than P(A) . (b) P(A B) exceeds P(A) . (c) P(A B)  0.72  0.84  0.52  1.04 exceeds 1 2.66 2 ,0 3 2.67 The area of the triangle is 4 3 6;  2  If the point is a distance x from the vertex on the longer leg, then is will be 3 x 4 units from the vertex on the other leg. The area of the required triangle is 3 3 2 4 2 8 x x x    . For this to be greater than 3, or half the area of the triangle, x2  8, or 2 x  2 . Thus, the probability of the line segment dividing the area in at least one-half is 4 2 2 2 1 4 2    2.68 0.21 0.28  0.15  0.34 2.69 (a) 0.59  0.30  0.21  0.68 ; (b) 0.59  0.21  0.38 (c) 1 0.21  0.79 ; (d) 1 0.68  0.32Chapter 2 17 ScholarStock 2.70 1 3 b  d  5 9 c  d  3 ; 4 a  b  c  hence 1 4 d  1 1 1 5 1 11 1 11 1 13 , , 1 3 4 12 9 4 36 12 36 4 36 b    c    a      a  P(out of state living on campus) b  P(out of state not living on campus) c  P(from Virginia living on campus) d  P(from Virginia not living on campus) 2.71 (a) (0.08)  0.05 0.02  0.11; (b) 1 [Show More]

Last updated: 2 years ago

Preview 1 out of 257 pages