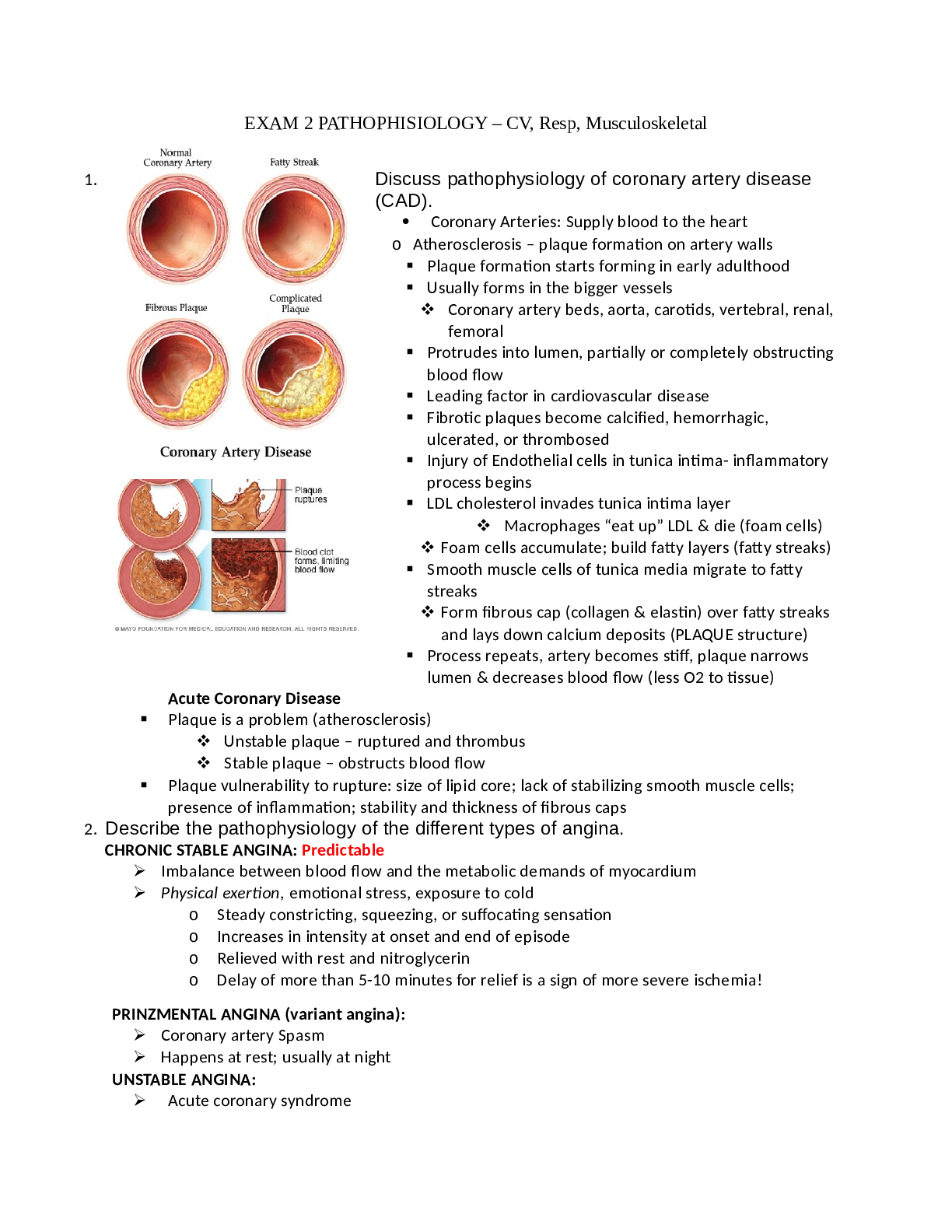
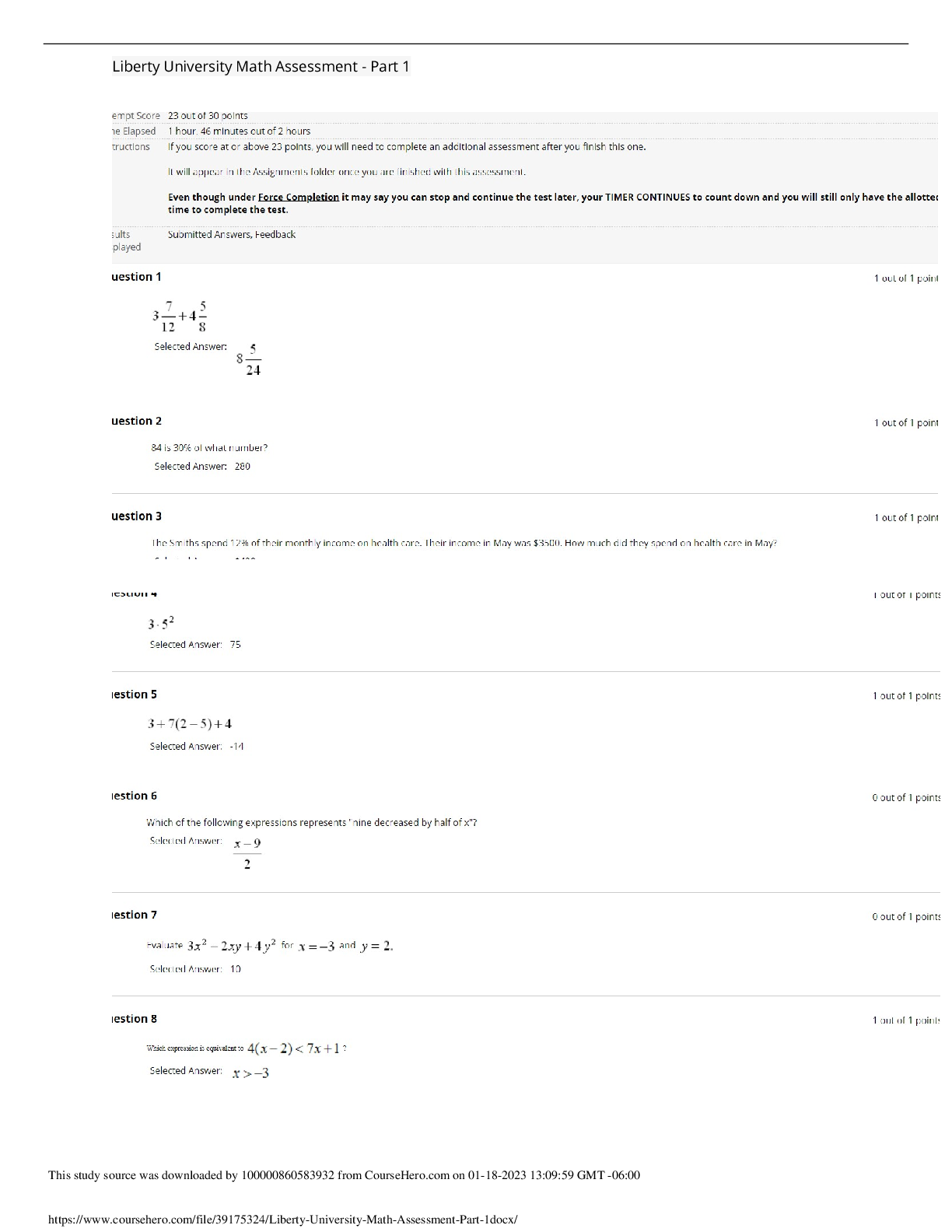
Introduction to Probability and Statistics Probability & Statistics for Engineers & Scientists, 8th Ed. 2007 | Handout #1

Introduction to Probability and Statistics Probability & Statistics for Engineers & Scientists, 8th Ed. 2007 Handout #1 Instructor: Kuo-Jung Lee TA: Brian Shea The pdf file for this class is available on the class ...

Introduction to Probability and Statistics Probability & Statistics for Engineers & Scientists, 8th Ed. 2007 Handout #1 Instructor: Kuo-Jung Lee TA: Brian Shea The pdf file for this class is available on the class web page. http://www.stat.umn.edu/~kjlee/STAT3021_Summer2009.html 1An Overview of Statistics 2What’s Statistics? Statistics is a way to get information from data 3Statistics is a discipline which is concerned with: • summarizing information to aid understanding, • drawing conclusions from data, • estimating the present or predicting the future, and • designing experiments and other data collection. In making predictions, Statistics uses the companion subject of Probability, which models chance mathematically and enables calculations of chance in complicated cases. 4Today, statistics has become an important tool in the work of many academic disciplines such as medicine, psychology, education, sociology, engineering and physics, just to name a few. Statistics is also important in many aspects of society such as business, industry and government. Because of the increasing use of statistics in so many areas of our lives, it has become very desirable to understand and practise statistical thinking. This is important even if you do not use statistical methods directly. 5Data Data consists of information coming from observation, counts, measurements, or responses. Statistics Statistics is the science of collecting, organizing, analyzing, and interpreting data in order to make decisions. 6Population A population is the collection of all outcomes, responses, measurements, or counts that are of interest. Sample A sample is a subset of a population. 7Parameter A parameter is numerical description of a population characteristics. Statistic A statistic is numerical description of a sample characteristic. 8Branches of Statistics Descriptive statistics is the branch of statistics that involves the organization, summarization, and display of data. Inferential statistics is the branch of statistics that involves using a sample to draw conclusions about a population. A basic tool in the study of inferential statistics is probability. 9Example A large sample of men, aged 48, was studied for 18 years. For unmarried men, 60% to 70% were alive at age 65. For married men, 90% were alive at age 65. Which part of the study represents the descriptive branch statistics? What conclusions might be drawn from this study using inferential statistics? 10Solution: Descriptive statistics: For unmarried men, 60% to 70% were alive at age 65. For married men, 90% were alive at age 65. A possible inference: Being married is associated with a longer life for men. 11Example An instructor is teaching two separate classes, A and B – each of size is 50. After a midterm, the scores for each class are: A: 50 47 59 49 72 41 63 79 91 65 49 59 92 42 34 43 53 89 76 93 89 51 42 46 67 48 33 47 68 51 56 53 69 53 43 36 58 85 45 64 57 32 1 60 66 60 63 86 62 55 B: 56 61 53 59 60 55 57 49 67 60 58 56 58 59 55 52 60 68 45 59 67 62 42 50 53 63 61 61 57 70 49 64 52 58 58 70 48 66 58 58 61 58 68 58 54 60 61 61 61 72 12Histogram of Scores for Class A Score Frequency 0 20 40 60 80 100 0 2 4 6 8 10 12 Histogram of Scores for Class B Score Frequency 40 45 50 55 60 65 70 75 0 5 10 15 13Class 1st Q Median 3rd Q Mean Standard Deviation A 47.00 56.50 66.75 58.34 18.24 B 55.25 58.50 61.00 58.56 6.29 14Chapter 2 Probability 15• Sample Space / Events • Counting Sample Points • Probability of an Event • Additive Rules • Conditional Probability • Multiplicative Rules • Bayes’ Rule 162.1 Sample Space 17Experiment Experiment is any process that generates a set of data. Sample space Sample space is the collection of all possible outcomes at a probability experiment. We use the notation S for sample space.