Energy CalculationsGCSE Physics. ALL QUESTIONS CALCULATIONS. DOWNLOAD TO SCORE A+. UNDERSTANDING GUARANTEED.

Document Content and Description Below

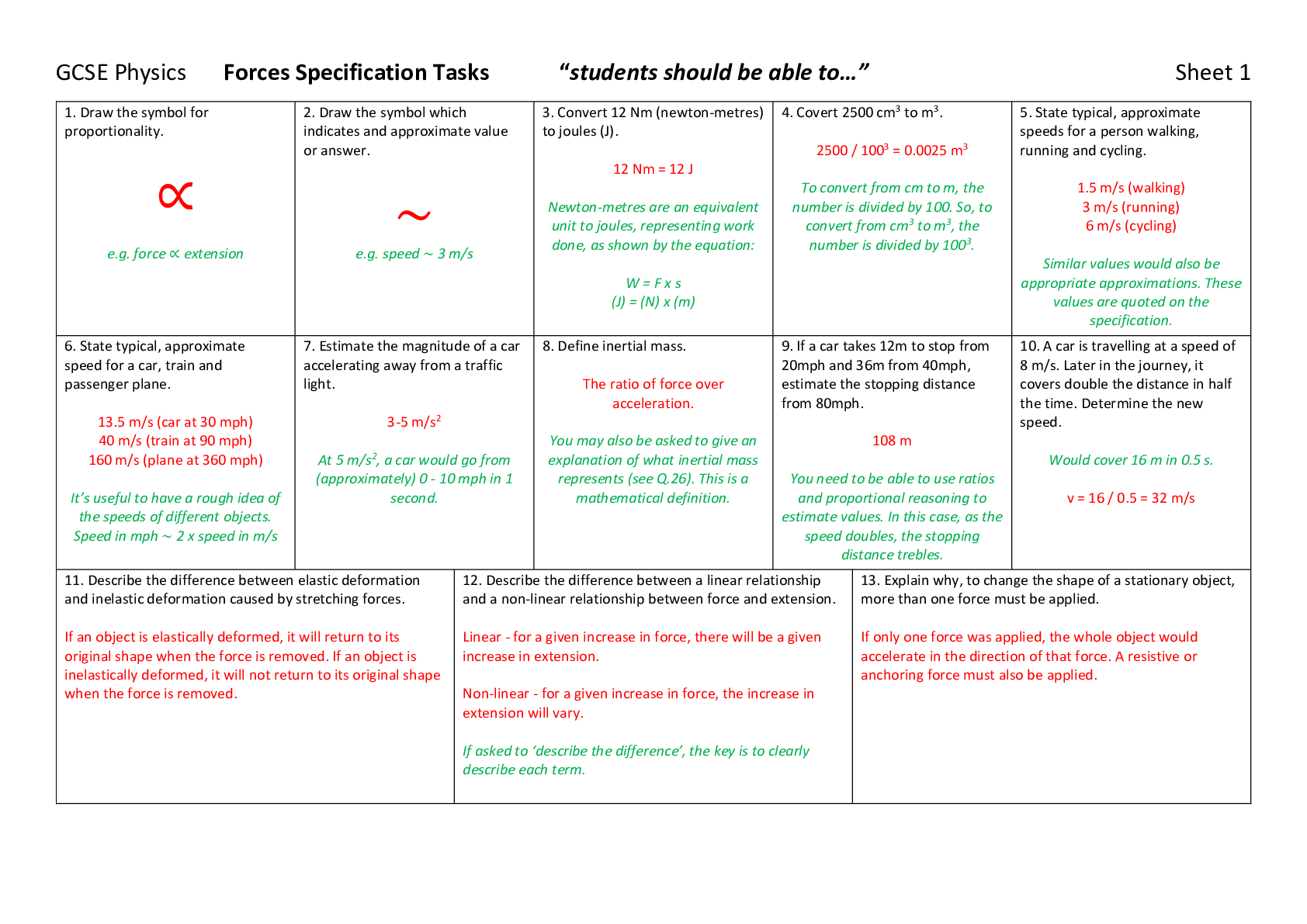
Calculate the kinetic energy of a 1200 g object travelling at 52 m/s. 1200 g = 1.2 kg KE = ½ mv2 KE = ½ x 1.2 x 522 KE = 1600 J Always convert units before starting to answer the question, an... d show your conversion clearly. 2. Calculate the velocity of a 800 kg car moving with 280 kJ of kinetic energy. 280 kJ = 280,000 J KE = ½ mv2 280000 = ½ x 800 x v2 v2 = 2 x 280000 / 800 v = 26 m/s It’s easy to forget to square root here, so think about whether your answer seems like a realistic value. 3. Calculate the elastic potential energy stored in a spring with a spring constant of 86 N/m when it is stretched by 13 cm. 13 cm = 0.13 m EPE = ½ ke2 EPE = ½ x 86 x 0.132 EPE = 0.73 J Remember that your answer isn’t correct if it doesn’t have units after it. 4. Calculate the spring constant of a spring that is storing 0.79 J of energy when stretched 12 cm. 12 cm = 0.12 m EPE = ½ ke2 0.79 = ½ x k x 0.122 k = 2 x 0.79 / 0.122 k = 110 N/m Always write the formula out, and substitute values before re-arranging. 5. Calculate the change in gravitational energy when a 3.7 kg object moves upwards 17 m. GPE = mgh GPE = 3.7 x 9.8 x 17 GPE = 620 J The value for the gravitational field strength, g, will be given to you in an exam, but it’s used so often that you should remember it anyway. 6. Calculate the increase in energy when 400 g of a liquid with a specific heat capacity of 2700 J/kg°C increases in temperature from 20°C to 58°C. 400 g = 0.4 kg ΔE = mcΔθ ΔE = 0.4 x 2700 x (58 - 20) ΔE = 41000 J The delta symbol, Δ, means a change in a quantity, and θ is used here to represent temperature. 7. Calculate the specific heat capacity of a 2.5 kg block of metal which absorbs 39 kJ of energy and increases in temperature by 20°C. 39 kJ = 39000 J ΔE = mcΔθ 39000 = 2.5 x c x 20 c = 39000 / (2.5 x 20) c = 780 J/kg°C 8. Calculate the power of a machine that transfers 240 kJ of energy in 3 minutes. 240 kJ = 240000 J 3 min = 180 s P = E / t P = 240000 / 180 P = 1300 W Another way that power is sometimes describe is the ‘rate of energy transfer’. Make sure you know this definition, and the alternative units of joules per second, J/s. 9. Calculate the speed of a 48 kg object that has fallen through a height of 26 m. Method 1 loss in GPE is equal to gain in KE GPE = mgh = 48 x 9.8 x 26 = 12200 J KE = ½ mv2 12200 = ½ x 48 x v2 v2 = 2 x 12200 / 48 v = 23 m/s Method 2 start with GPE = KE mgh = ½ mv2 48 x 9.8 x 26 = ½ x 48 x v2 v2 = 2 x 9.8 x 26 v = 23 m/s 10. Calculate the efficiency of an electric motor which uses 7.4 kJ of energy to lift a 34 kg object 11 m. 7.4 kJ = 7400 J efficiency = useful energy / total energy input useful energy = increase in GPE useful energy = mgh = 34 x 9.8 x 11 = 3700 J efficiency = 3700 / 7400 efficiency = 0.5 (50 %) In efficiency calculations, you may have to figure out what the useful energy transfer is and work that out separately. 11. Calculate the maximum height that could be reached by a 87 g object fired from a catapult with a spring constant of 200 N/m when it has been stretched 27 cm. 87 g = 0.087 kg 27 cm = 0.27 m elastic potential energy is transferred to GPE EPE = ½ ke2 = ½ x 200 x 0.272 = 7.29 J GPE = mgh 7.29 = 0.087 x 9.8 x h h = 7.29 / (0.087 x 9.8) = 8.6 m It’s useful to write down the energy transfer as the starting point for calculations like this.GCSE Physics Energy Calculations “students should be able to…” Sheet 2 1. Calculate the kinetic energy of a 1900 g object travelling at 74 m/s. 1900 g = 1.9 kg KE = ½ mv2 KE = ½ x 1.9 x 742 KE = 5200 J Always convert units before starting to answer the question, and show your conversion clearly. 2. Calculate the velocity of a 1800 kg car moving with 920 kJ of kinetic energy. 920 kJ = 920,000 J KE = ½ mv2 920000 = ½ x 1800 x v2 v2 = 2 x 920000 / 1800 v = 32 m/s It’s easy to forget to square root here, so think about whether your answer seems like a realistic value. 3. Calculate the elastic potential energy stored in a spring with a spring constant of 55 N/m when it is stretched by 13 cm. 13 cm = 0.13 m EPE = ½ ke2 EPE = ½ x 55 x 0.132 EPE = 0.46 J Remember that your answer isn’t correct if it doesn’t have units after it. 4. Calculate the spring constant of a spring that is storing 0.49 J of energy when stretched 6 cm. 6 cm = 0.06 m EPE = ½ ke2 0.49 = ½ x k x 0.062 k = 2 x 0.49 / 0.062 k = 270 N/m Always write the formula out, and substitute values before re-arranging. 5. Calculate the change in gravitational energy when a 9.8 kg object moves upwards 13 m. GPE = mgh GPE = 9.8 x 9.8 x 13 GPE = 1200 J The value for the gravitational field strength, g, will be given to you in an exam, but it’s used so often that you should remember it anyway. 6. Calculate the increase in energy when 180 g of a liquid with a specific heat capacity of 3700 J/kg°C increases in temperature from 23°C to 89°C. 180 g = 0.18 kg ΔE = mcΔθ ΔE = 0.18 x 3700 x (89 - 23) ΔE = 44000 J The delta symbol, Δ, means a change in a quantity, and θ is used here to represent temperature. 7. Calculate the specific heat capacity of a 2.1 kg block of metal which absorbs 20 kJ of energy and increases in temperature by 22°C. 20 kJ = 20000 J ΔE = mcΔθ 20000 = 2.1 x c x 22 c = 20000 / (2.1 x 22) c = 430 J/kg°C 8. Calculate the power of a machine that transfers 210 kJ of energy in 6 minutes. 210 kJ = 210000 J 6 min = 360 s P = E / t P = 210000 / 360 P = 580 W Another way that power is sometimes describe is the ‘rate of energy transfer’. Make sure you know this definition, and the alternative units of joules per second, J/s. 9. Calculate the speed of a 50 kg object that has fallen through a height of 14 m. Method 1 loss in GPE is equal to gain in KE GPE = mgh = 50 x 9.8 x 14 = 6860 J KE = ½ mv2 6860 = ½ x 50 x v2 v2 = 2 x 6860 / 50 v = 17 m/s Method 2 start with GPE = KE mgh = ½ mv2 50 x 9.8 x 14 = ½ x 50 x v2 v2 = 2 x 9.8 x 14 v = 17 m/s 10. Calculate the efficiency of an electric motor which uses 7.5 kJ of energy to lift a 29 kg object 14 m. 7.5 kJ = 7500 J efficiency = useful energy / total energy input useful energy = increase in GPE useful energy = mgh = 29 x 9.8 x 14 = 4000 J efficiency = 4000 / 7500 efficiency = 0.53 (53 %) In efficiency calculations, you may have to figure out what the useful energy transfer is and work that out separately. 11. Calculate the maximum height that could be reached by a 64 g object fired from a catapult with a spring constant of 320 N/m when it has been stretched 29 cm. 64 g = 0.064 kg 29 cm = 0.29 m elastic potential energy is transferred to GPE EPE = ½ ke2 = ½ x 320 x 0.292 = 13.5 J GPE = mgh 13.5 = 0.064 x 9.8 x h h = 13.5 / (0.087 x 9.8) = 22 m It’s useful to write down the energy transfer as the starting point for calculations like this.GCSE Physics Energy Calculations “students should be able to…” Sheet 3 1. Calculate the kinetic energy of a 1500 g object travelling at 50 m/s. 1500 g = 1.5 kg KE = ½ mv2 KE = ½ x 1.5 x 502 KE = 1900 J Always convert units before starting to answer the question, and show your conversion clearly. 2. Calculate the velocity of a 2200 kg car moving with 1320 kJ of kinetic energy. 1320 kJ = 1,320,000 J KE = ½ mv2 1320000 = ½ x 2200 x v2 v2 = 2 x 1320000 / 2200 v = 35 m/s It’s easy to forget to square root here, so think about whether your answer seems like a realistic value. 3. Calculate the elastic potential energy stored in a spring with a spring constant of 43 N/m when it is stretched by 24 cm. 24 cm = 0.24 m EPE = ½ ke2 EPE = ½ x 43 x 0.242 EPE = 1.2 J Remember that your answer isn’t correct if it doesn’t have units after it. 4. Calculate the spring constant of a spring that is storing 0.29 J of energy when stretched 5 cm. 5 cm = 0.05 m EPE = ½ ke2 0.29 = ½ x k x 0.052 k = 2 x 0.29 / 0.052 k = 230 N/m Always write the formula out, and substitute values before re-arranging. 5. Calculate the change in gravitational energy when a 3.9 kg object moves upwards 14 m. GPE = mgh GPE = 3.9 x 9.8 x 14 GPE = 540 J The value for the gravitational field strength, g, will be given to you in an exam, but it’s used so often that you should remember it anyway. 6. Calculate the increase in energy when 240 g of a liquid with a specific heat capacity of 3900 J/kg°C increases in temperature from 25°C to 37°C. 240 g = 0.24 kg ΔE = mcΔθ ΔE = 0.24 x 3900 x (37 - 25) ΔE = 11000 J The delta symbol, Δ, means a change in a quantity, and θ is used here to represent temperature. 7. Calculate the specific heat capacity of a 1.9 kg block of metal which absorbs 33 kJ of energy and increases in temperature by 15°C. 33 kJ = 33000 J ΔE = mcΔθ 33000 = 1.9 x c x 15 c = 33000 / (1.9 x 15) c = 1200 J/kg°C 8. Calculate the power of a machine that transfers 260 kJ of energy in 3 minutes. 260 kJ = 260000 J 3 min = 180 s P = E / t P = 260000 / 180 P = 1400 W Another way that power is sometimes describe is the ‘rate of energy transfer’. Make sure you know this definition, and the alternative units of joules per second, J/s. 9. Calculate the speed of a 154 kg object that has fallen through a height of 48 m. Method 1 loss in GPE is equal to gain in KE GPE = mgh = 154 x 9.8 x 48 = 72400 J KE = ½ mv2 72400 = ½ x 154 x v2 v2 = 2 x 72400 / 154 v = 31 m/s Method 2 start with GPE = KE mgh = ½ mv2 154 x 9.8 x 48 = ½ x 154 x v2 v2 = 2 x 9.8 x 48 v = 31 m/s 10. Calculate the efficiency of an electric motor which uses 6.9 kJ of energy to lift a 29 kg object 15 m. 6.9 kJ = 6900 J efficiency = useful energy / total energy input useful energy = increase in GPE useful energy = mgh = 29 x 9.8 x 15 = 4300 J efficiency = 4300 / 6900 efficiency = 0.62 (62 %) In efficiency calculations, you may have to figure out what the useful energy transfer is and work that out separately. 11. Calculate the maximum height that could be reached by a 67 g object fired from a catapult with a spring constant of 310 N/m when it has been stretched 30 cm. 67 g = 0.067 kg 30 cm = 0.3 m elastic potential energy is transferred to GPE EPE = ½ ke2 = ½ x 310 x 0.32 = 14 J GPE = mgh 14 = 0.067 x 9.8 x h h = 14 / (0.087 x 9.8) = 21 m [Show More]

Last updated: 2 years ago

Preview 1 out of 101 pages