Chapter 12: Business Analytics_ Data Analysis _ Decision Making

Document Content and Description Below

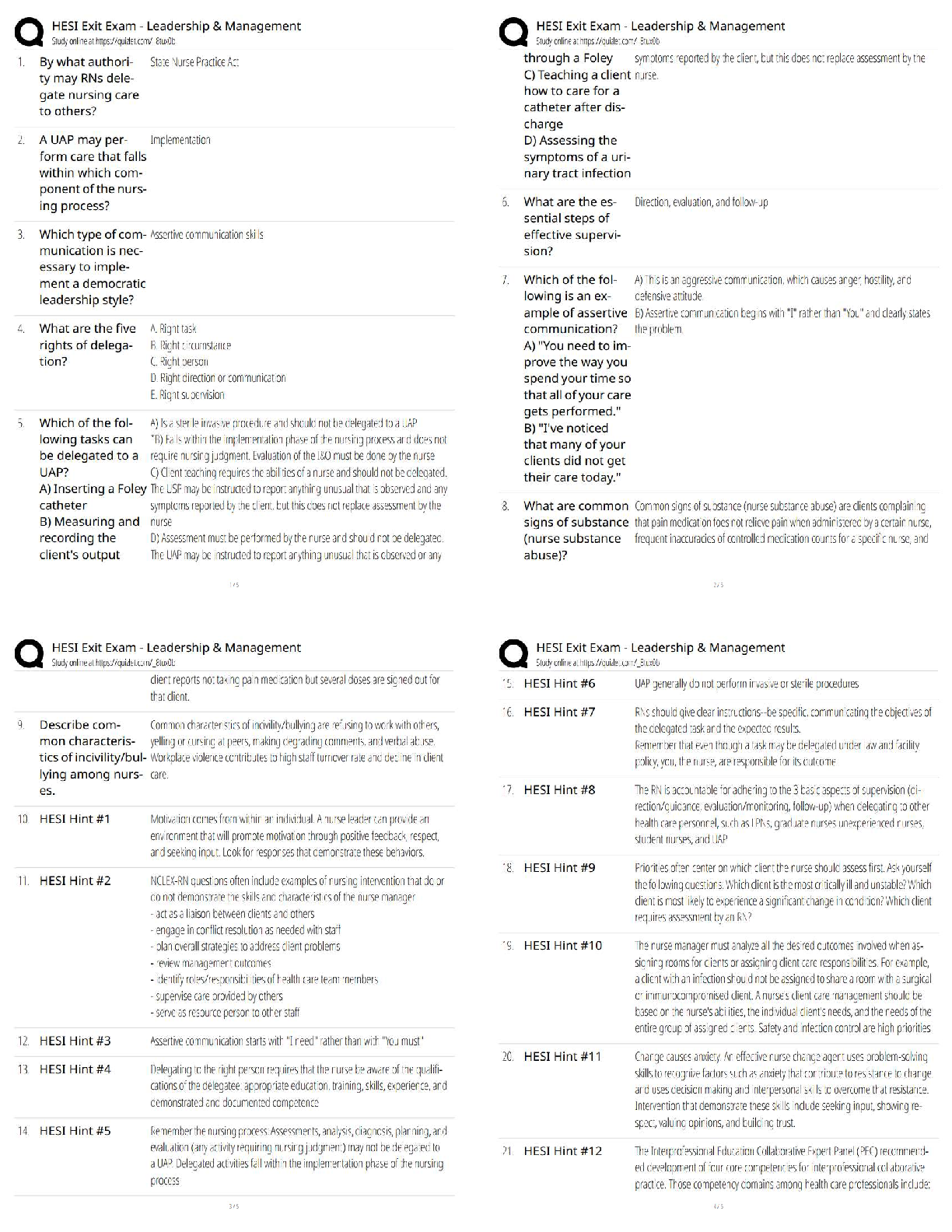
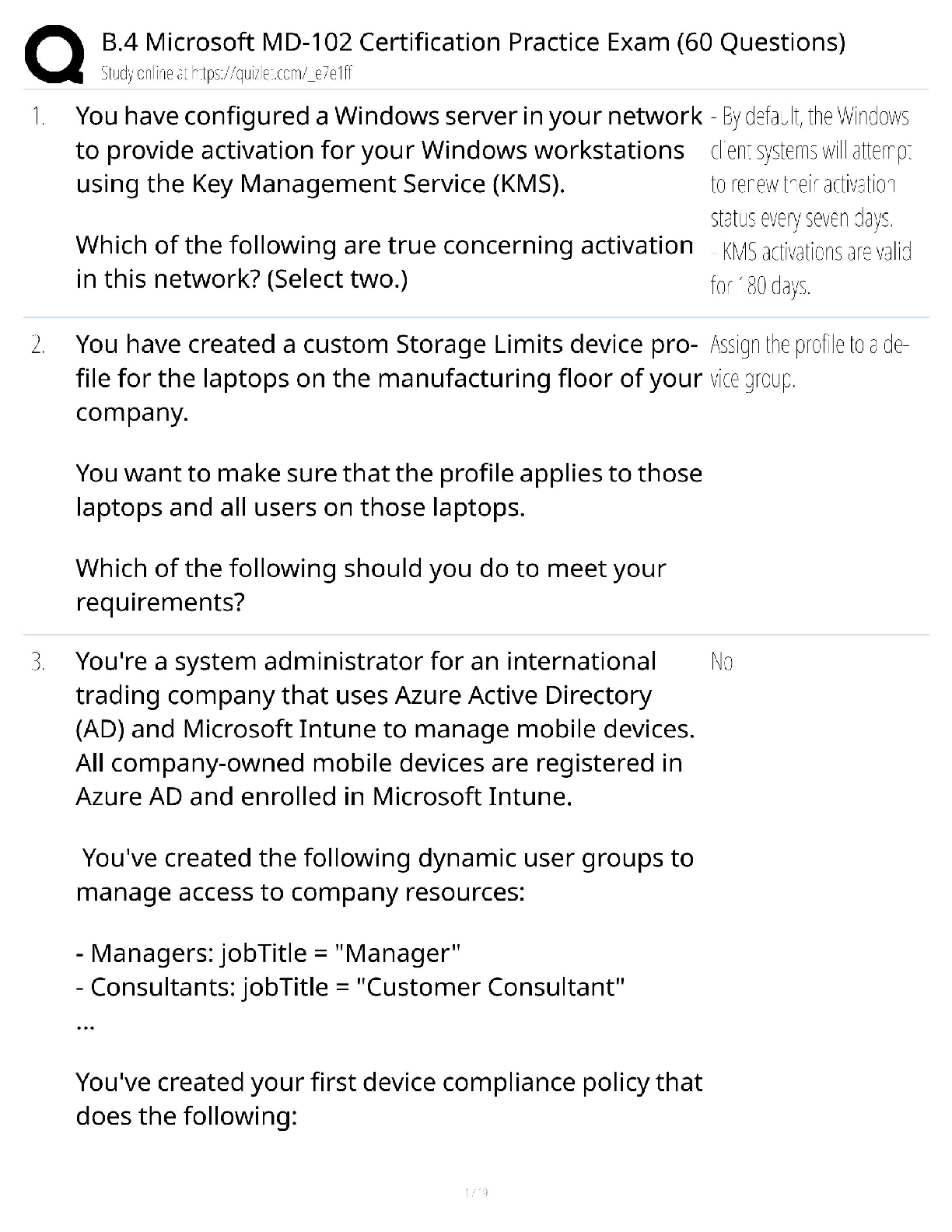
1. Forecasting models can be divided into three groups. They are: a. time series, optimization, and simulation methods b. judgmental, extrapolation, and econometric methods c. judgmental, random, a... nd linear methods d. linear, non-linear, and extrapolation methods 2. Extrapolation methods attempt to: a. use non-quantitative methods to predict future values b. search for patterns in the data and then use those to predict future values c. find variables that are correlated with the data being predicted d. predict the next period’s value by using the latest period’s value 3. Econometric models can also be called: a. judgmental models b. time series models c. causal models d. environmetric models 4. Models such as moving average, exponential smoothing, and linear trend use only: a. future values of Y to forecast previous values of Y b. previous values of Y to forecast future values of Y c. multiple explanatory variables (not just values of Y) to forecast future values of Y d. ratio-to-moving-average methods 5. The components of a time series include: a. base series b. trend c. seasonal component d. cyclic component e. all of these options : Chapter 12 6. The forecast error is the difference between a. this period’s value and the next period’s value b. the average value and the expected value of the response variable c. the explanatory variable value and the response variable value d. the actual value and the forecast 7. Which of the following is not one of the summary measures for forecast errors that is commonly used? a. MAE (mean absolute error) b. MFE (mean forecast error) c. RMSE (root mean square error) d. MAPE (mean absolute percentage error) 8. Which of the following summary measures for forecast errors does not depend on the units of the forecast variable? a. MAE (mean absolute error) b. MFE (mean forecast error) c. RMSE (root mean square error) d. MAPE (mean absolute percentage error) 9. Examples of non-random patterns that may be evident on a time series graph include: a. trends b. increasing variance over time c. a meandering pattern d. too many zigzags e. all of these options 10. Which of the following is not one of the techniques that can be used to identify whether a time series is truly random? a. A graph (plot the data) b. The runs test c. A control chart d. The autocorrelations (or a correlogram) Chapter 12 11. Related to the runs test, if you use a Z-statistic and you get a Z value greater than 2.0, this means that there is evidence of _____in the series a. randomness b. nonrandomness c. nonnormality d. heteroscedasticity 12. The runs test uses a series of 0’s and 1’s. The 0’s and 1’s represent whether each observation is: a. above or below the predicted value of Y b. above or below the mean value of Y c. is above or below the mean value of the previous two observations d. is positive or negative 13. The idea behind the runs test is that a random number series should have a number of runs that is: a. large b. small c. not large or small d. constant 14. Related to the runs test, if T is reasonably large (T > 20 is suggested), then the statistic can be used to perform this test. a. F b. t c. Z d. 15. In a random series, successive observations are probabilistically independent of one another. If this property is violated, the observations are said to be: a. autocorrelated b. intercorrelated c. causal d. seasonal Chapter 12 16. The most common form of autocorrelation is positive autocorrelation, in which: a. large observations tend to follow both large and small observations b. small observations tend to follow both large and small observations c. large observations tend to follow large observations and small observations tend to follow small observations d. large observations tend to follow small observations and small observations tend to follow large observations 17. A linear trend means that the time series variable changes by a: a. constant amount each time period b. constant percentage each time period c. positive amount each time period d. negative amount each time period 18. The linear trend was estimated using a time series with 20 time periods. The forecasted value for time period 21 is a. 120 b. 122 c. 160 d. 162 19. In contrast to linear trend, exponential trend is appropriate when the time series changes by a: a. constant amount each time period b. constant percentage each time period c. positive amount each time period d. negative amount each time period 20. The random walk model is written as: . In this model, represents the: a. average of the Y’s b. average of the X’s c. forecasted value d. random series with mean 0 and some constant standard deviation Chapter 12 21. In a random walk model the a. series itself is random b. series itself is not random but its differences are random c. series itself and its differences are random d. series itself and its differences are not random 22. Perhaps the simplest and one of the most frequently used extrapolation methods is the: a. moving average b. linear trend c. exponential trend d. causal model 23. The moving average method can also be referred to as a (n) method. a. causal b. smoothing c. exponential d. econometric 24. When using the moving average method, you must select which represent(s) the number of terms in the moving average. a. a smoothing constant b. the explanatory variables c. an alpha value d. a span 25. The following are the values of a time series for the first four time periods: t 1 2 3 4 24 25 26 27 Using a four-period moving average, the forecasted value for time period 5 is: a. 24.5 b. 25.5 c. 26.5 d. 27.5 Chapter 12 26. The data below represents sales for a particular product. If you were to use the moving average method with a span of 3 periods, what would be your forecast for period 5? Period Sales (in units) 1 90 2 120 3 110 4 100 a. 90 b. 100 c. 105 d. 110 27. The data below represents sales for a particular product. If you were to use the moving average method with a span of 4 periods, what would be your forecast for period 5? Period Sales (in units) 1 90 2 120 3 110 4 100 a. 90 b. 100 c. 105 d. 110 28. When using exponential smoothing, a smoothing constant must be used. The value for : a. ranges between 0 and 1 b. ranges between –1 and +1 c. equals the largest observed value in the series d. represents the strength of the association between the forecasted and observed values 29. When using exponential smoothing, if you want the forecast to react quickly to movements in the series, you should choose: a. values of near 1 b. values of near 0 c. values of midway between 0 and 1 d. it depends on the data set 30. Suppose that a simple exponential smoothing model is used (with = 0.40) to forecast monthly sandwich sales at a local sandwich shop. The forecasted demand for September was 1560 and the actual demand was 1480 sandwiches. Given this information, what would be the forecast number of sandwiches for October? a. 1480 b. 1528 c. 1560 d. 1592 31. Suppose that a simple exponential smoothing model is used (with a = 0.30) to forecast monthly sandwich sales at a local sandwich shop. After June’s demand is observed at 1520 sandwiches, the forecasted demand for July is 1600 sandwiches. At the beginning of July, what would be the forecasted demand for August? a. 1520 b. 1544 c. 1550 d. 1600 32. Holt’s model differs from simple exponential smoothing in that it includes a term for: a. seasonality b. trend c. residuals d. cyclical fluctuations 33. When using Holt’s model, choosing values of the smoothing constant that are near 1 will result in forecast models which a. react very quickly to changes in the level b. react very quickly to changes in the trend c. react very quickly to changes in the level and the trend d. react very slowly to changes in the level and the trend 34. Which of the following is not a method for dealing with seasonality in data a. Winter’s exponential smoothing model b. deseasonalizing the data, using any forecasting model, then reseasonalizing the data c. multiple regression with lags for the seasons d. multiple regression with dummy variables for the seasons Chapter 12 35. Winters’ model differs from Holt’s model and simple exponential smoothing in that it includes an index for: a. seasonality b. trend c. residuals d. cyclical fluctuations 36. There are a variety of deseasonalizing methods, but they are typically variations of: a. ratio-to-seasonality methods b. ratio-to-exponential-smoothing methods c. ratio-to-moving-average methods d. linear trend 37. A regression approach can also be used to deal with seasonality by using variables for the seasons. a. smoothing b. response c. residual d. dummy 38. A time series is any variable that is measured over time in sequential order. a. True b. False 39. A time series can consist of four different components: trend, seasonal, cyclical, and random (or noise). a. True b. False 40. A trend component of a time series is a long-term, relatively smooth pattern or direction exhibited by a series, and its duration is more than one year. a. True b. False 41. If the observations of a time series increase or decrease regularly through time, we say that the time series has a random (or noise) component. a. True b. False alse Chapter 12 42. The time series component that reflects a long-term, relatively smooth pattern or direction exhibited by a time series over a long time period, is called seasonal. a. True b. False alse 43. The time series component that reflects a wavelike pattern describing a long-term trend that is generally apparent over a number of years is called cyclical. a. True b. False 44. The seasonal component of a time series is harder to predict than the cyclic component; the reason is that cyclic variation is much more regular. a. True b. False alse 45. The cyclic component of a time series is more likely to exhibit business cycles that record periods of economic recession and inflation. a. True b. False 46. Econometric forecasting models, also called causal models, use regression to forecast a time series variable by using other explanatory time series variables. a. True b. False 47. Extrapolation forecasting methods are quantitative methods that use past data of a time series variable – and nothing else, except possible time itself – to forecast values of the variable. a. True b. False 48. You will always get more accurate forecasts by using more complex forecasting methods. a. True b. False 49. Forecasting software packages typically report several summary measures of the forecasting error. The most important of these are MAE (mean absolute error), RMSE (root mean square error), and MAPE (mean absolute percentage error). a. True b. False 50. A shortcoming of the RMSE (root mean square error) is that it is not in the same units as the forecast variable. a. True b. False alse 51. As is the case with residuals from regression, the forecast errors for nonregression methods will always average to zero a. True b. False alse 52. A meandering pattern is an example of a random time series. a. True b. False alse 53. The runs test is a formal test of the null hypothesis of randomness. If there are too many or too few runs in the series, then we conclude that the series is not random. a. True b. False 54. If a random series has too few runs, then it is zigzagging too often. a. True b. False alse 55. The null hypothesis in a runs test is the data series is random a. True b. False 56. An autocorrelation is a type of correlation used to measure whether the values of a time series are related to their own past values. a. True b. False 57. The most common form of autocorrelation is positive autocorrelation, where large observations tend to follow large observations and small observations tend to follow small observations. a. True b. False 58. The trend line was calculated from quarterly data for 2000 – 2004, where t = 1 for the first quarter of 2000. The trend value for the second quarter of the year 2005 is 0.75. a. True b. False alse 59. An exponential trend is appropriate when the time series changes by a constant percentage each period. a. True b. False 60. If a time series exhibits an exponential trend, then a plot of its logarithm should be approximately linear. a. True b. False 61. An equation for the random walk model is given by the equation: , where is the change in the time series from time t to time t – 1, is a constant, and is a random variable (noise) with mean 0 and some standard deviation . a. True b. False 62. In a random walk model, there are significantly more runs than expected, and the autocorrelations are not significant. a. True b. False 63. Correlogram is a bar chart of autocorrelation at different lags. a. True b. False 64. The moving average method is perhaps the simplest and one of the most frequently-used extrapolation methods. a. True b. False 2. 65. A moving average is the average of the observations in the past few periods, where the number of terms in the average is the span. a. True b. False 66. The purpose of using the moving average is to take away the short-term seasonal and random variation, leaving behind a combined trend and cyclical movement. a. True b. False 67. We compute the five-period moving averages for all time periods except the first two. a. True b. False alse 68. To calculate the five-period moving average for a time series, we average the values in the two preceding periods, and the values in the three following time periods. a. True b. False alse 69. If the span of a moving average is large – say, 12 months – then few observations go into each average, and extreme values have relatively large effect on the forecasts. a. True b. False 70. The smoothing constant used in simple exponential smoothing is analogous to the span in moving averages. a. True b. False 71. Every form of exponential smoothing model has at least one smoothing constant, which is always between 0 and 1. a. True b. False 72. The smoothing constants in exponential smoothing models are effectively a way to assign different weights to past levels, trends and cycles in the data. a. True b. False 73. Simple exponential smoothing is appropriate for a series without a pronounced trend or seasonality. a. True b. False 74. In exponential smoothing models, the forecast is based on the level at time t, Lt, which is not observable and can only be estimated. a. True b. False 75. If we use a value close to 1 for the smoothing constant in a simple exponential smoothing model, then we expect the model to respond very slowly to changes in the level. a. True 3. b. False alse 76. Holt’s method is an exponential smoothing method, which is appropriate for a series with seasonality and possibly a trend. a. True b. False 77. If we use a value close to 1 for the level smoothing constant and a value close to 0 for the trend smoothing constant in Holt’s exponential smoothing model, then we expect the model to respond very quickly to changes in the level, but very slowly to changes in the trend. a. True b. False alse 78. The seasonal component of a time series is more likely to exhibit the relatively steady growth of a variable, such as the population of Egypt from 35 million in 1960 to 75 million in 2005. a. True b. False alse 79. To deseasonalize an observation (assuming a multiplicative model of seasonality), multiply it by the appropriate seasonal index. a. True b. False alse 80. Seasonal variations will not be present in a deseasonalized time series. a. True b. False 81. Winter’s method is an exponential smoothing method, which is appropriate for a series with trend but no seasonality. a. True b. False alse 82. In an additive seasonal model, we add an appropriate seasonal index to a “base” forecast. These indexes, one for each season, typically average to 0. a. True b. False 83. In a multiplicative seasonal model, we multiply a “base” forecast by an appropriate seasonal index. These indexes, one for each season, typically average to 1. a. True b. False Copyright Cengage Learning. Powered by Cognero. Page 14 Name: Class: Date: Chapter 12 84. In a regression model with seasonal dummy variables, the coefficients on the dummy variables represent the additive factor relative to the reference quarter value, not the multiplicative factor. a. True b. False 86. We compare the percent of variation explained R2 for a regression model with seasonal dummy variables to the MAPE for the smoothing model with seasonality to see which model is more accurate. a. True b. False 87. Rite Aid pharmacy in Big Rapids, Michigan is using simple exponential smoothing to predict monthly birthday card sales. At the end of October 2004, the pharmacy’s forecast for December 2004 sales was 400. In November, 420 cards were sold, and during December, 425 cards were sold. At the end of December 2004, what is the pharmacy’s forecast for the total number of cards that will be sold during March and April of 2005? Use . ds. The data shown below contains total monthly retail sales (in dollars) a small sporting goods store for the years 2006– 2008. 88. Obtain a time series graph of the data. If you will be using a moving average model of the data, what information does this graph provide to help specify such a model? 89. Use the method of moving averages with an appropriate span to forecast retail sales for the first half of 2009. Do you 90. Run the moving average fit again, this time holding out the last 6 observations to validate the fit. What do you find? 91. What changes, if any, would you suggest to improve the forecast? lthough this deseasonalized moving average model provides a good fit and reliable forecast, we do note a slight upward trend in the data. Since this cannot be captured by a moving average model, we might also want to try Holt’s method. 92. A car dealer in Big Rapids, Michigan is using Holt’s method to forecast weekly car sales. Currently the level is estimated to be 45 cars per week, and the trend is estimated to be 5 cars per week. During the current week, 25 cars are sold. After observing the current week’s sales, forecast the number of cars three weeks from now. Use . The number of employees on the payroll at a computer software company is recorded at the start of each month from January 2007 to December 2009. These data are shown below. Year Jan Feb March April May June July Aug. Sept. Oct. Nov. Dec 2007 348 352 330 347 339 370 380 392 400 410 405 367 2008 350 341 345 355 342 350 370 395 410 401 405 365 2009 348 349 350 350 342 377 369 400 410 406 400 370 93. Develop a time series plot of the data. Does the data appear random on the plot? 94. Perform a runs test and compute a few autocorrelations to determine whether this time series is random. Copyright Cengage Learning. Powered by Cognero. Page 19 Name: Class: Date: Chapter 12 95. Use the method of moving averages with an appropriate span to forecast retail sales for 2010. Do you obtain a good fit? Do you have confidence in your forecast? Explain your answers. 96. At the beginning of April, what is the forecast of June’s Pepsi sales? orecast for June is 5000 cans. 97. (A) Suppose that actual demands during April and May are as follows: May, 5500 cans; June 4500 cans. After observing May’s demand, what is the forecast for June’s demand? (B) Based on the data from (A), the demands during April and May average (5500+4500)/2 = 5000 cans per month. This is the same as the forecast for monthly sales before we observed the April and May data. Yet after we observed the April and May demands for Pepsi, our forecast for June demand has decreased from what it was at the end of March. Why? 98. (A) Use Excel to generate a time series of 25 values using this random walk model with a starting value of 200. (B) Conduct a runs test on the series you generated for (A). Is it random? Explain. (C) Conduct a runs test on the differences between successive values for the series you generated for (A). Is it random? Explain. (D) Use the time series you constructed in (A) to forecast the next observation.. Page 21 [Show More]

Last updated: 2 years ago

Preview 1 out of 35 pages