Chapter 13: Business Analytics_ Data Analysis _ Decision Making

Document Content and Description Below

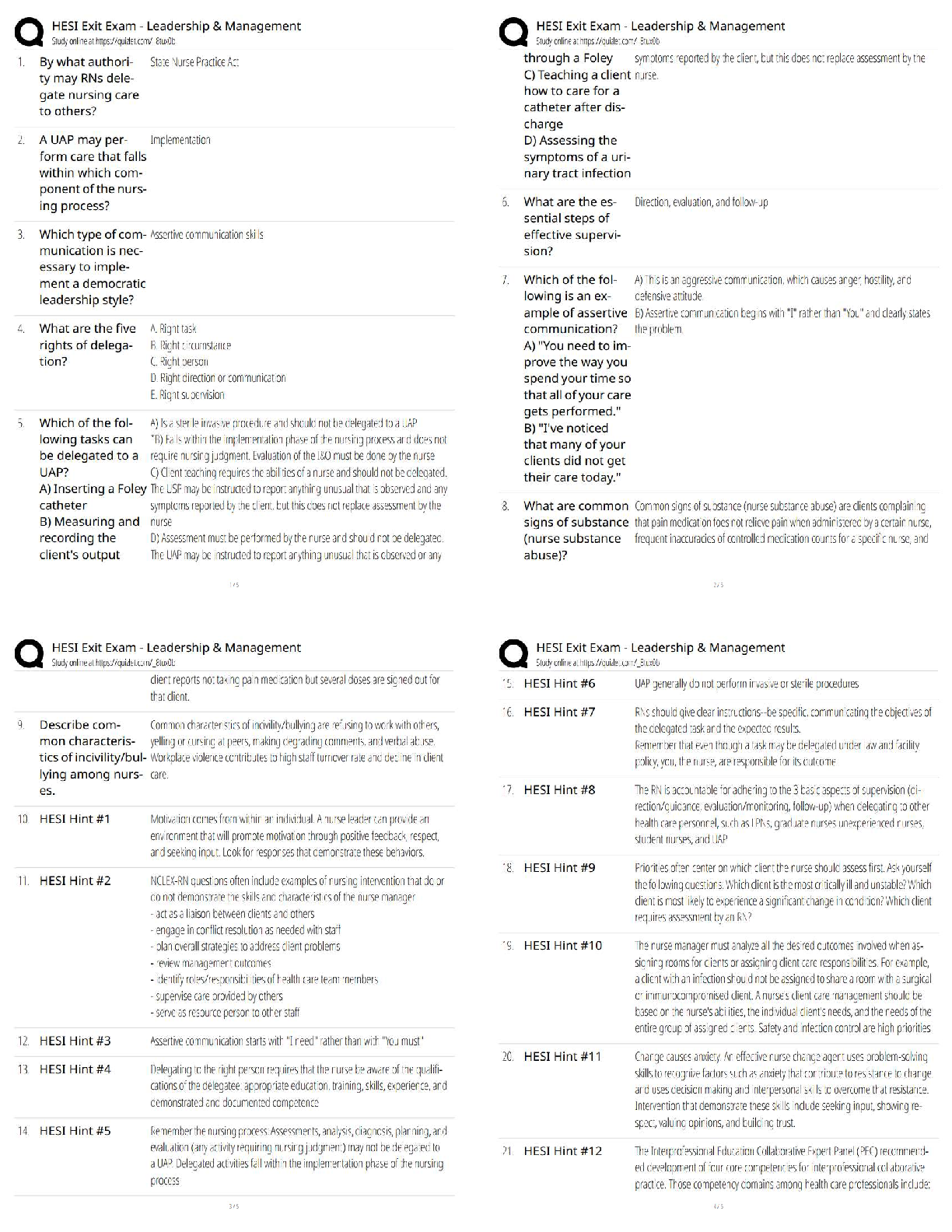
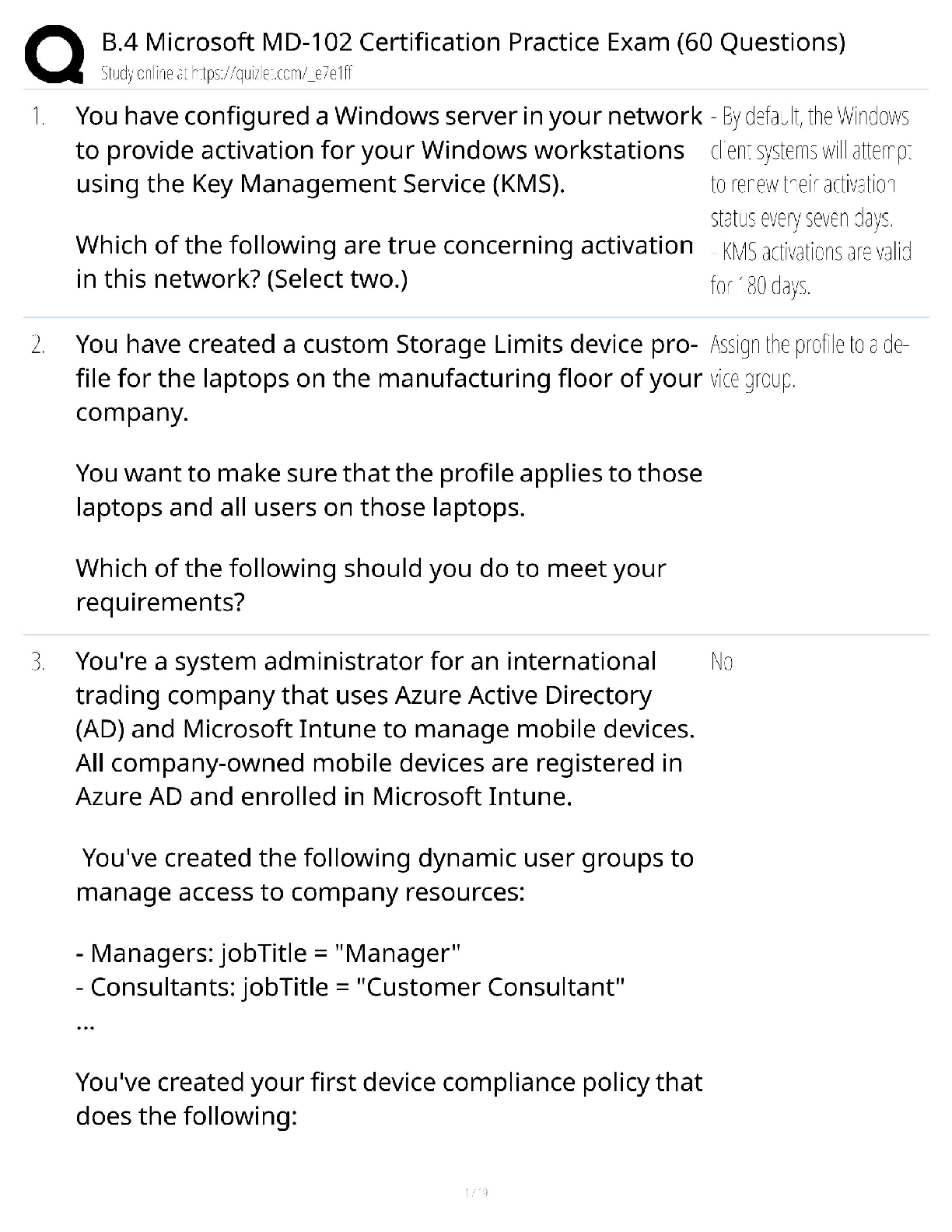
Name: Class: Date: Chapter 13 1. T... he set of all values of the changing cells that satisfy all constraints, not including the nonnegativity constraints, is called the feasible region. 2. Linear programming is a subset of a larger class of models called: 3. In using Excel to solve linear programming problems, the target cell represents the: 4. In linear programming, sensitivity analysis involves examining how sensitive the optimal solution is to changes in: 5. Related to sensitivity analysis in linear programming, when the profit increases with a unit increase in a resource, this change in profit is referred to as the: 6. In linear programming we can use the shadow price to calculate increases or decreases in: 7. Shadow prices are associated with nonbinding constraints, and show the change in the optimal objective function value when the right side of the constraint equation changes by one unit. 8. Reduced costs indicate how much the objective coefficient of a decision variable that is currently 0 or at its upper bound must change before that the value of that variable changes. 9. Suppose the allowable increase and decrease for an objective coefficient of a decision variable that has a current value of $50 are $25 (increase) and $10 (decrease). If the coefficient were to change from $50 to $60, the optimal value of the objective function would not change. 10. Suppose the allowable increase and decrease for shadow price for a constraint are $25 (increase) and $10 (decrease). If the right hand side of that constraint were to increase by $10 the optimal value of the objective function would change. 11. It is often useful to perform sensitivity analysis to see how, or if, the optimal solution to a linear programming problem changes as we change one or more model inputs. 12. Proportionality, additivity, and divisibility are three important properties that LP models possess, which distinguish them from general mathematical programming models:. 13. The divisibility property of LP models simply means that we allow only integer levels of the activities. A farmer in Egypt owns 50 acres of land. He is going to plant each acre with cotton or corn. Each acre planted with cotton yields $400 profit; each with corn yields $200 profit. The labor and fertilizer used for each acre are given in the table below. Resources available include 150 workers and 200 tons of fertilizer. Copyright Cengage Learning. Powered by Cognero. Page 2 Name: Class: Date: Chapter 13 Cotton Corn Labor (Workers) 5 3 Fertilizer (Tons) 6 2 14. (A) Formulate a linear programming model that will enable the farmer to determine the number of acres that should be planted cotton and/or corn in order to maximize his profit. (B) Find an optimal solution to the model in (A) and determine the maximum profit. (C) Implement the model in (A) in Excel Solver and obtain an answer report. Which constraints are binding on the optimal solution? (D) Obtain a sensitivity report for the model in (A). How much should the farmer be willing to pay for an additional worker? (E) Suppose the farmer hires 10 additional workers. Can you use the sensitivity analysis obtained for (D) to determine his expected profit? Would his planting plan change? Explain your answer. (F) Suppose the farmer now wants to hire 20 additional workers, instead of just 10. Can you use the sensitivity analysis obtained for (D) to determine his expected profit? Explain your answer. 15. What are the decision variables in this problem? 16. (A) Find an optimal solution to the problem. What is the production plan, and what is the total revenue? (B) Obtain a sensitivity report for the solution reported in (A). Which constraints are binding? (C) What is the incremental contribution associated with adding an hour of assembly time? Over what range of increase is the marginal value valid? (D) What is the value of additional capacity on the polisher? How much increase and decrease in this capacity is possible before a change occurs in the optimal production schedule? (E) An advertising agency has devised a marketing plan for the Valley Chassis Company that will increase the market for Deluxe chassis. The plan will increase demand by 75 Deluxe chassis per month at a cost of $100 per month. Should Valley adopt the plan? Briefly explain why. (F) Suppose that four more hours of chassis assembly time could be made available. How much would profit change? (G) Suppose next that Valley’s marketing department proposes lowering the price for a standard chassis from $12 to $11.50 so that more can be sold (since there is slack under the demand constraint). Would the optimal solution change? Explain why, or why not. (H) If Valley could obtain 1,000 pounds more of raw material (steel or aluminum), which should it procure? How much should they be willing to pay per pound for the steel or aluminum? Explain your answer. (I) In doing some contingency planning, Valley thinks that the aging stamping machine will soon need to be taken down for repairs that could last 2 months and will cost $10,000. During that time, they can continue to operate by outsourcing the stamping at $2.50 per chassis (deluxe or standard), although the capacity will be reduced from 2,500 to 1,500. What will be the total cost to repair the stamping machine? ANSWER: (A) (B) Copyright Cengage Learning. Powered by Cognero. Page 5 Name: Class: Date: Chapter 13 Steel available, Aluminum available, Assembly SS, and Market Deluxe SS all have nonzero shadow prices, so they are binding. (C) Incremental contribution is $2 per hour, with an allowable increase of 25 hours. (D) The value of additional capacity on the polisher is zero, since it is not binding. The allowable increase is unbounded, and the allowable decrease is 1000. (E) The change in the profit would be $1.8/hour shadow price times 75 hours, or $135, so Valley should adopt the plan. (F) Profit would increase by $8 (4 hours times $2/hour shadow price) (G) The optimal solution would not change, because the change in the objective coefficient is within the allowable decrease (-$0.8). Note that since this would not result in any more standard chassis being sold, profit would decrease by $400. (H) They should procure 1,000 pounds more of aluminum, since the shadow price is higher than that for steel (0.6 vs. 0.4). This results in additional profit of $600. (I) The total cost will be the sum of the repairs ($10,000), the outsourcing cost ($2.50 per chassis, extended by how ever many chassis will be produced) and any reduction in profit due to the restricted stamping capacity. Note that since the capacity reduction on stamping is greater than the allowable decrease, a new production plan will be required. This new plan (0 SS, 4,000 AS, 500 SC, 1,000 DC) results in profit of $23,400, which is a reduction of $2,800 from the existing optimal profit of $26,200. With the production plan determined, the outsourcing cost can be determined (500 SC + 1000 DC = 1500 * $2.50 = $3,750). Thus the total cost will be $10,000 + 2 months*($2,800 + $3,750) = $23,100. Copyright Cengage Learning. Powered by Cognero. Page 6 Name: Class: Date: Chapter 13 A customer requires 50, 65, 100, and 70 units of a commodity during the next 4 months, respectively, and no backlogging is allowed; that is, the customer’s requirements must be met on time. Production costs $5, $8, $4, and $7 per unit during these months. The storage cost from one month to the next is $2 per unit (assessed on ending inventory). It is estimated that each unit on hand at the end of month 4 could be sold for $6. 17. (A) Determine how to minimize the net cost incurred in meeting the demands for the next four months. (B) Starting with the optimal solution to (A), use SolverTable add-in to see what happens to the decision variables and the total cost when the initial inventory varies from 0 (the implied value in (A)) to 100 in 10-units increments. How much lower would the total cost be if the company started with 10 units in inventory, rather than none? Would the same cost decrease occur for every 10-init increase in initial inventory? 18. (A) Determine how to minimize the cost of meeting the demand for the next three weeks. (B) Revise the model in (A) so that the demands are of the form , where is the original demand in month t, k Copyright Cengage Learning. Powered by Cognero. Page 7 Name: Class: Date: Chapter 13 is a factor, and is an amount of change in month t. Formulate the model in such a way that you can use the SolverTable add-in to analyze changes in the amounts produced and the total cost when k varies from 0 to 10 in 1-unit increments, for any fixed values of the ’s. For example, try this when = 2, = 5, and = 3. Describe the behavior you observe in the table. Can you find any “reasonable” ’s that induce positive production levels in week 3?. 19. (A) Determine how to minimize the total cost of meeting the next 3 quarters’ demand. Assume that 1000 usable units are available at the beginning of quarter 1. (B) Referring to (A), the company wants to know how much money it would be worth to decrease the percentage of unsuitable items and/or the percentage of items that spoil. Write a short report that provides relevant information. Base your report on two uses of the SolverTable add-in: one where the percentage of unsuitable items decreases and the percentage of items that spoil stays at 10%; and one where the percentage of unsuitable items stays at 20% and the percentage of items that spoil decreases. Chapter 13 20. (A) Verify that Mary should purchase 12 units of food 2 each day and thus oversatisfy the vitamin C requirement by 6 units. (B) Mary’s husband has put his foot down and demanded that Mary fulfill the family’s daily nutritional requirement exactly by obtaining precisely 12 units of vitamin A and 6 units of vitamin C. The optimal solution to the new problem will involve ingesting less vitamin C, but it will be more expensive, why? (C) Starting with the optimal solution to (B), use the SloverTable add-in to see what happens to the total cost when the vitamin A and vitamin C requirements both vary (independently) from 3 to 18 in 3-unit increments. That is, from a twoway table. Describe the behavior you observe. In particular, are the changes in total cost the same as you look across each row of the table? Are they the same as you look across each column of the table? Copyright Cengage Learning. Powered by Cognero. Page 11 Name: Class: Date: Chapter 13 Adam Enterprises manufactures two products. Each product can be produced on either of two machines. The time (in hours) required to make each product on each machine is shown below: Each month, 500 hours of time are available on each machine, and also customers are willing to buy up to the quantities of each product at the prices shown below: The company’s goal is to maximize the revenue obtained from selling units during the next two months. Copyright Cengage Learning. Powered by Cognero. Page 12 Name: Class: Date: Chapter 13 21. (A) Determine how the company can meet its goal. Assume that Adam will not produce any units in either month that it cannot sell in that month. (B) Referring to (A), suppose Adam wants to see what will happen if customer demands for each product in each month simultaneously change by a factor 1 + k. Revise the model so that you can use the SolverTable add-in to investigate the effect of this change on total revenue as k varies from -0.3 to 0.3 in increments of 0.1. Does revenue change in a linear manner over this range? Can you explain intuitively why it changes in the way it does? 22. What are the decision variables in this problem?23. (A) Write out algebraic expressions for all of the constraints in this problem. (B) Construct a graph of the feasible region for this problem, given the constraints you identified in (A). (C) Describe how you would find the location of the optimal solution in the feasible region you graphed in (B). (D) Use the procedure you described in (C) to identify the optimal production plan. Confirm your solution using Solver. What is the maximized profit? (E) What constraints are binding on the optimal solution? Use your graphical solution to explain your answer. 24. Write out an algebraic expression for the objective function in this problem. 25. All optimization problems have: a. an objective function and decision variables b. an objective function and constraints c. decision variables and constraints d. an objective function, decision variables and constraints 26. In an optimization model, there can only be one: 27. The most important solution method for linear programming problems is known as the: 28. Every linear programming problem involves optimizing a: 29. In using Excel to solve linear programming problems, the changing cells represent the: Chapter 13 30. The term nonnegativity refers to the condition where: 31. In most cases in solving linear programming problems, we want the decision variables to be: 32. When using the graphical solution method to solve linear programming problems, the set of points that satisfy all constraints is called the: 33. The feasible region in all linear programming problems is bounded by: 34. All optimization problems include decision variables, an objective function, and constraints. b. Faa. True lse alse 35. All linear programming problems should have a unique solution, if they can be solved. a. True b. False alse 36. There is often more than one objective in linear programming problems a. True b. False alse Copyright Cengage Learning. Powered by Cognero. Page 17 Name: Class: Date: Chapter 13 37. There are generally two steps in solving an optimization problem, model development and optimization. a. True b. False alse 38. When formulating a linear programming spreadsheet model, there is a set of designated cells that play the role of the decision variables. These are called the objective cells. a. True b. False alse 39. When formulating a linear programming spreadsheet model, there is one target (objective) cell that contains the value of the objective function. a. True b. False 40. It is instructive to look at a graphical solution procedure for LP models with three or more decision variables. a. True b. False alse 41. The feasible region in a graphical solution of a linear programming problem will appear as some type of polygon, with lines forming all sides. a. True b. False 42. The solution of a linear programming problem using Microsoft Excel typically involves the following three stages: a. formulating the problem, invoking Solver, and sensitivity analysis b. formulating the problem, graphing the problem, and sensitivity analysis c. the changing cells, the target cells, and the constraints d. the inputs, the changing cells, and the outputs 43. The prototype linear programming problem is to select an optimal mix of products to produce to maximize profit. This type of problem is referred to as the: a. product mix problem b. production problem c. product/process problem d. product scheduling problem Copyright Cengage Learning. Powered by Cognero. Page 18 Name: Class: Date: Chapter 13 44. A linear programming problem with _____decision variable(s) can be solved by a graphical solution method. a. 1 b. 2 c. 3 d. 4 45. The optimal solution to any linear programming model is: a. the maximum objective function line b. the minimum objective function line c. the corner point of a polygon d. the maximum or minimum of a parabola 46. Suppose a company sells two different products, x and y, for net profits of $5 per unit and $10 per unit, respectively. The slope of the line representing the objective function is: a. 0.5 b. -0.5 c. 2 d. -2 47. The equation of the line representing the constraint is: a. b. c. d. 48. The equation of the line representing the constraint passes through the points: a. b. c. d. 49. In general, the complete solution of a linear programming problem involves three stages: formulating the model, invoking Solver to find the optimal solution, and performing sensitivity analysis. a. True b. False Copyright Cengage Learning. Powered by Cognero. Page 19 Name: Class: Date: Chapter 13 50. There are two primary ways to formulate a linear programming problem, the traditional algebraic way and in spreadsheets. a. True b. False 51. Linear programming problems can always be formulated algebraically, but not always on spreadsheet. a. True b. False alse 52. When formulating a linear programming spreadsheet model, we specify the constraints in a Solver dialog box, since Excel does not show the constraints directly. a. True b. False 53. The optimal solution to any linear programming model is a corner point of a polygon. a. True b. False alse 54. In determining the optimal solution to a linear programming problem graphically, if the objective is to maximize the objective, we pull the objective function line down until it contacts the feasible region. a. True b. False 55. Suppose a liquor store sells beer for a net profit of $1 per unit and wine for a net profit of $2 per unit. Let x equal the amount of beer sold and y equal the amount of wine sold. An algebraic formulation of the profit function is: a. b. c. d. Copyright Cengage Learning. Powered by Cognero. Page 20 Name: Class: Date: Chapter 13 56. If a manufacturing process takes 3 hours per unit of x and 5 hours per unit of y and a maximum of 100 hours of manufacturing process time are available, then an algebraic formulation of this constraint is: a. b. c. d. 57. Suppose a firm must at least meet minimum expected demands of 60 for product x and 80 of product y. An algebraic formulation of these constraints is: a. b. c. d. 58. If the objective function has the equation , then the slope of the objective function line is 2: a. True b. False alse 59. If the objective function has the equation , then the y-intercept of the objective function line is 40: a. True b. False alse 60. If a constraint has the equation , then the slope of the constraint line is function line is -2: a. True b. False 61. If a constraint has the equation , then the constraint line passes through the points (0,20) and (30,0): a. True b. False alse Copyright Cengage Learning. Powered by Cognero. Page 21 Name: Class: Date: Chapter 13 62. Nonbinding constraints will always have slack, which is the difference between the two sides of the inequality in the constraint equation. a. True b. False Sinclair Plastics operates two chemical plants which produce polyethylene; the Ohio Valley plant which produces 5000 tons per month and the Lakeview plant which can produce 7000 tons per month. Sinclair sells its polyethylene to three different GM auto plants, Grand Rapids (demand = 3000 tons per month), Blue Ridge (demand = 5000 tons per month), and Sunset (demand = 4000 tons per month). The costs of shipping between the respective plants is shown in the table below: Grand Rapids Blue Ridge Sunset Ohio Valley 50 40 100 Lakeview 75 50 75 63. What are the decision variables in this problem? 64. What are the decision variables in this problem? 65. What is the objective function in this problem? 66. What are the constraints in this problem? Copyright Cengage Learning. Powered by Cognero. Page 23 Name: Class: Date: Chapter 13 67. Find an optimal solution to the problem, assuming that the company will not produce any units in either month that it cannot sell in that month. What is the production plan, and what is the total revenue? ANSWER: The plan in the first month is to make 120 units of Product 1 on Machine 1 and 120 units of Product 2 on Machine 2. In the second month, 104 units of Product 1 will be made using Machine 1 and 130 total units of Product 2 will be made (10 on Machine 1 and 120 on Machine 2). The total revenue is $21,710. Copyright Cengage Learning. Powered by Cognero. Page 24 Name: Class: Date: Chapter 13 Sinclair Plastics operates two chemical plants which produce polyethylene; the Ohio Valley plant which produces 5000 tons per month and the Lakeview plant which can produce 7000 tons per month. Sinclair sells its polyethylene to three different GM auto plants, Grand Rapids (demand = 3000 tons per month), Blue Ridge (demand = 5000 tons per month), and Sunset (demand = 4000 tons per month). The costs of shipping between the respective plants is shown in the table below: Grand Rapids Blue Ridge Sunset Ohio Valley 50 40 100 Lakeview 75 50 75 68. What is the objective function in this problem? 69. What are the decision variables in this problem? 70. What are the constraints in this problem? Name: Class: Date: Chapter 13 Sinclair Plastics operates two chemical plants which produce polyethylene; the Ohio Valley plant which produces 5000 tons per month and the Lakeview plant which can produce 7000 tons per month. Sinclair sells its polyethylene to three different GM auto plants, Grand Rapids (demand = 3000 tons per month), Blue Ridge (demand = 5000 tons per month), and Sunset (demand = 4000 tons per month). The costs of shipping between the respective plants is shown in the table below: Grand Rapids Blue Ridge Sunset Ohio Valley 50 40 100 Lakeview 75 50 75 71. What are the constraints in this problem? 72. What is the optimal shipping plan? What are the total costs in that case? 73. What is the objective function in this problem? 74. Linear programming models have three important properties. They are: a. optimality, additivity and sensitivity b. optimality, linearity and divisibility c. divisibility, linearity and nonnegativity d. proportionality, additivity and divisibility Copyright Cengage Learning. Powered by Cognero. Page 26 Name: Class: Date: Chapter 13 75. The additivity property of linear programming implies that the contribution of any decision variable to the objective is of/on the levels of the other decision variables. a. dependent b. independent c. conditional d. the sum 76. The divisibility property of linear programming means that a solution can have both: a. integer and noninteger levels of an activity b. linear and nonlinear relationships c. positive and negative values d. revenue and cost information in the model 77. The proportionality property of LP models means that if the level of any activity is multiplied by a constant factor, then the contribution of this activity to the objective function, or to any of the constraints in which the activity is involved, is multiplied by the same factor. a. True b. False 78. When the proportionality property of LP models is violated, then we generally must use non-linear optimization. a. True b. False 79. The additivity property of LP models implies that the sum of the contributions from the various activities to a particular constraint equals the total contribution to that constraint. a. True b. False 80. It helps to ensure that Solver can find a solution to a linear programming problem if the model is well-scaled; that is, all of the numbers are of roughly the same magnitude. a. True b. False Copyright Cengage Learning. Powered by Cognero. Page 27 Name: Class: Date: Chapter 13 81. When there is a problem with Solver being able to find a solution, many times it is an indication of a (n): a. older version of Excel b. nonlinear programming problem c. problem that cannot be solved using linear programming d. mistake in the formulation of the problem 82. In some cases, a linear programming problem can be formulated such that the objective can become infinitely large (for a maximization problem) or infinitely small (for a minimization problem). This type of problem is said to be: a. infeasible b. inconsistent c. unbounded d. redundant 83. Unboundedness refers to the situation in which the LP model has been formulated in such a way that the objective function is unbounded – that is, it can be made as large (for maximization problems) or as small (for minimization problems) as we like. a. True b. False 84. Infeasibility refers to the situation in which there are no feasible solutions to the LP model a. True b. False 85. If an LP model does have an unbounded solution, then we must have made a mistake – either we made an input error or we omitted one or more constraints. a. True b. False 86. If a solution to an LP problem satisfies all of the constraints, then is must be feasible. a. True b. False Copyright Cengage Learning. Powered by Cognero. Page 28 Name: Class: Date: Chapter 13 87. Consider the following linear programming problem: Maximize Subject to The above linear programming problem: a. has only one optimal solution b. has more than one optimal solution c. exhibits infeasibility d. exhibits unboundedness 88. Consider the following linear programming problem: Maximize Subject to The above linear programming problem: a. has only one optimal solution b. has more than one optimal solution c. exhibits infeasibility d. exhibits unboundedness Copyright Cengage Learning. Powered by Cognero. Page 29 Name: Class: Date: Chapter 13 89. Consider the following linear programming problem: Maximize Subject to The above linear programming problem: a. has only one optimal solution b. has more than one optimal solution c. exhibits infeasibility d. exhibits unboundedness 90. Consider the following linear programming problem: Minimize Subject to The above linear programming problem: a. has only one optimal solution b. has more than one optimal solution c. exhibits infeasibility d. exhibits unboundedness 91. One of the things that you can do with linear programming and a spreadsheet model is to develop a user interface to make it easier for someone who is not an expert in using linear programming. The output can be a report that explains the optimal policy in non-technical terms. The type of system being described is called a (n): a. expert system b. decision support system c. linear programming support system d. production planning system A marketing research professor is conducting a telephone survey and needs to contact at least 160 wives, 140 husbands, 110 single adult males, and 120 single adult females. It costs $2 to make a daytime call and $4 (because of higher labor costs) to make an evening call. The table shown below lists the expected results. For example, 10% of all daytime calls are answered by a single male, and 15% of all evening calls are answered by a single female. Because of a limited staff, at most half of all phone calls can be evening calls. Determine how to minimize the cost of completing Copyright Cengage Learning. Powered by Cognero. Page 30 Name: Class: Date: Chapter 13the survey. Percentages Daytime Evening Wife 25% 25% Husband 15% 30% Single male 10% 25% Single female 15% 15% None 35% 5% 92. (A) What is the objective function in this problem? (B) What are the constraints in this problem? Write an algebraic expression for each. (C) Find an optimal solution to the problem using the formulation given in (A) and (B). What is the call plan, and what is the total cost? (D) Implement the model in (C) in Excel Solver and obtain an answer report. Which constraints are binding on the optimal solution? (E) Obtai a sensitivity report for the model in (D). If the professor could cut the cost of evening calls from $4 to $3, what would the new calling plan be? (F) Again using the sensitivity report obtained for (E), suppose the professor could get by with just 100 calls for single females. What would the call costs be in that case? Explain your answer. [Show More]

Last updated: 2 years ago

Preview 1 out of 32 pages