BUS 660 Chapter 4 Homework Problems 1, 2, 5, 7, 9, 13, 14, 15, 17, 19, 21, 25 You scored 88.70% on Retake

Document Content and Description Below

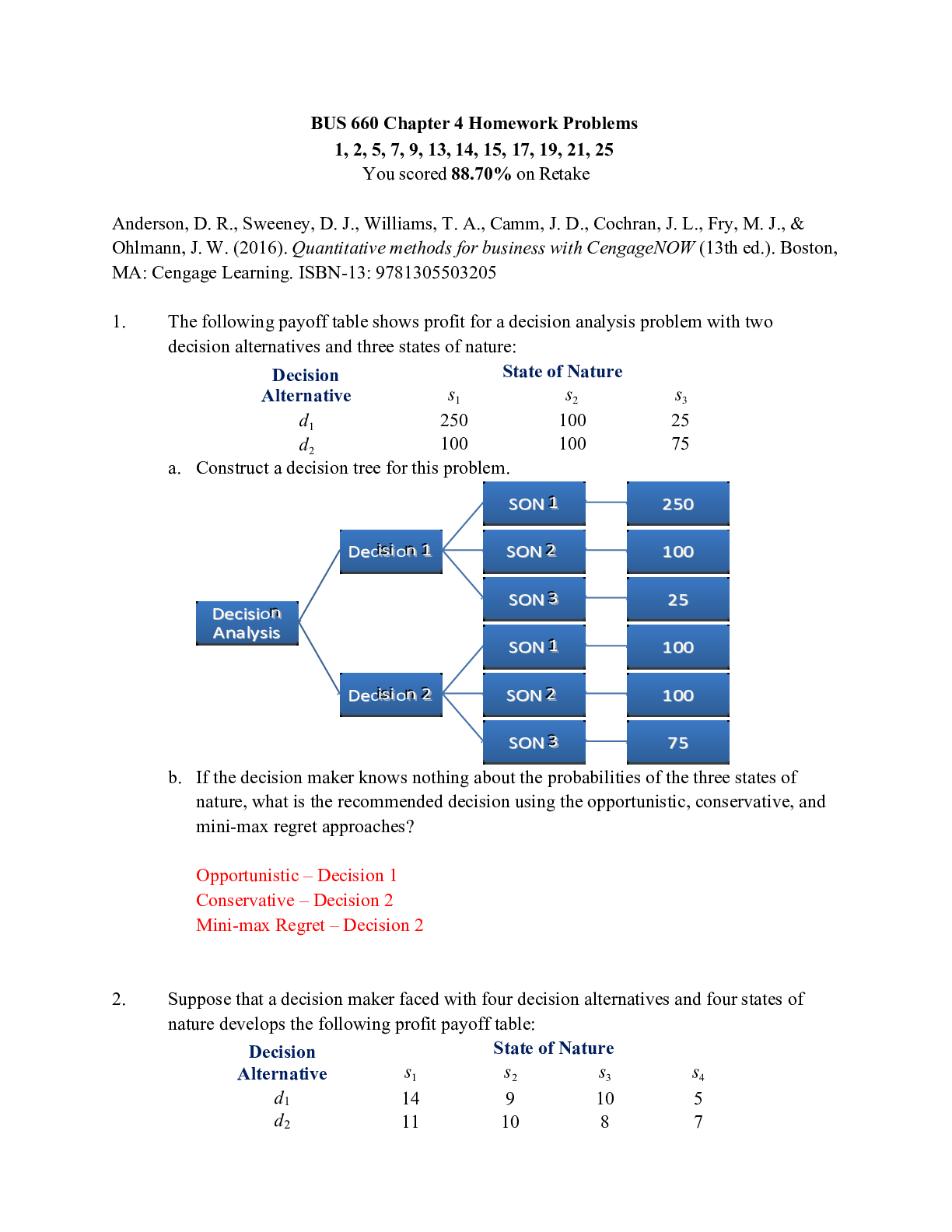
BUS 660 Chapter 4 Homework Problems 1, 2, 5, 7, 9, 13, 14, 15, 17, 19, 21, 25 You scored 88.70% on RetakeSON 111 250 Deciiisssiiionnn 111 SON 222 100 SON 333 25 Decisionnn Analysis SON 111 100 ... Deciiisssiiionnn 222 SON 222 100 SON 333 75 BUS 660 Chapter 4 Homework Problems 1, 2, 5, 7, 9, 13, 14, 15, 17, 19, 21, 25 You scored 88.70% on Retake Anderson, D. R., Sweeney, D. J., Williams, T. A., Camm, J. D., Cochran, J. L., Fry, M. J., & Ohlmann, J. W. (2016). Quantitative methods for business with CengageNOW (13th ed.). Boston, MA: Cengage Learning. ISBN-13: 9781305503205 1. The following payoff table shows profit for a decision analysis problem with two decision alternatives and three states of nature: Decision State of Nature Alternative s1 s2 s3 d 1 250 100 25 d2 100 100 75 a. Construct a decision tree for this problem. b. If the decision maker knows nothing about the probabilities of the three states of nature, what is the recommended decision using the opportunistic, conservative, and mini-max regret approaches? Opportunistic – Decision 1 Conservative – Decision 2 Mini-max Regret – Decision 2 2. Suppose that a decision maker faced with four decision alternatives and four states of nature develops the following profit payoff table: Decision Alternative State of Nature s 1 s2 s3 s4 d1 14 9 10 5 d2 11 10 8 7d3 9 10 10 11 d4 8 10 11 13 a. If the decision maker knows nothing about the probabilities of the four states of nature, what is the recommended decision using the optimistic, conservative, and mini-max regret approaches? Opportunistic – Decision 1 Conservative – Decision 3 Mini-max Regret – Decision 3 b. Which approach do you prefer? Explain. I prefer the minimax approach because I believe that it offers more consideration for both the best and worst scenario. Is establishing the most appropriate approach before analyzing the problem important for the decision maker? Explain. Yes, because that allows time and resources conservation and increases the likelihood of a sound decision. c. Assume that the payoff table provides cost rather than profit payoffs. What is the recommended decision using the optimistic, conservative, and mini-max regret approaches? Opportunistic – Decision 1 Conservative – Decision 1 Mini-max Regret – Decision 3 7. Hudson Corporation is considering three options for managing its data processing operation: continuing with its own staff, hiring an outside vendor to do the managing (referred to as outsourcing), or using a combination of its own staff and an outside vendor. The cost of the operation depends on future demand. The annual cost of each option (in thousands of dollars) depends on demand as follows: a. If the demand probabilities are 0.2, 0.5, and 0.3, which decision alternative will minimize the expected cost of the data processing operation? What is the expected annual cost associated with that recommendation? D1 = Own Staff D2 = Outside VendorD3 = Combo EV d1 = (.2*650) + (.5*650) + (.3*600) = 635 EV d2 = (.2*900) + (.5*600) + (.3*300) = 570 EV d3 = (.2*800) + (.5*650) + (.3*500) = 635 b. Construct a risk profile for the optimal decision in part (a). What is the probability of the cost exceeding $700,000? Cost Probability 900 .2 600 .5 300 .3 The probability of cost greater than & 700 is 0.2 5. In American football, touchdowns are worth 6 points. After scoring a touchdown, the scoring team may subsequently attempt to score 1 or 2 additional points. Going for 1 point is virtually an assured success, while going for 2 points is successful only with probability p. Consider the following game situation. The Temple Wildcats are losing by 14 points to the Killeen Tigers near the end of regulation time. The only way for Temple to win (or tie) this game is to score two touchdowns while not allowing Killeen to score again. The Temple coach must decide whether to attempt a 1-point or 2-point conversion after each touchdown. If the score is tied at the end of regulation time, the game goes into overtime. The Temple coach believes that there is a 50% chance that Temple will win if the game goes into overtime. The probability of successfully converting a 1-point conversion is 1.0. The probability of successfully converting a 2-point conversion is p. a. Assume Temple will score two touchdowns and Killeen will not score. Create a decision tree for the decision of whether Temple's coach should go for a 1-point conversion or a 2-point conversion after each touchdown. The terminal nodes in the decision tree should be either WIN or LOSE for Temple.shouldnotgo b. Assume that a WIN results in a value of 1.0 and LOSE results in a value of 0. Further, assume that the probability of converting a 2-point conversion is p = 39%. Should Temple's coach go for a 1-point conversion or 2-point conversion after scoring the first touchdown? The Temple coach should not go for 2 points after the first touchdown. For Temple to win there are three possibilities, 1)To score two touchdowns-12 points+2 1pt =14 points->draw+50% probability of winning in over time 2)To score two touchdowns-12pts+1 pt +2 pt=15 points->win 3)To score two touchdowns-12pts+2 pt=16 points->win Lets calculate the probability of winning in each case: 1)Probability=1*1*0.5=0.5 2)Probability=1*0.4*2 =0.8 3)Probability=0.4^2 =0.16 But if we see after the first touchdown, Probability to win if i take a 1 point->0.5+0.4 =0.9 Probability to win if i take 2 point->0.4*(1+0.4*0.5)+0.6*(0.4*0.5)=0.6 Hence there is a more probability to win if i take the 1 point in the first attempt. 9. Myrtle Air Express decided to offer direct service from Cleveland to Myrtle Beach. Management must decide between a full-price service using the company’s new fleet of jet aircraft and a discount service using smaller capacity commuter planes. It is clear that the best choice depends on the market reaction to the service Myrtle Air offers. Management developed estimates of the contribution to profit for each type of service based upon two possible levels of demand for service to Myrtle Beach: strong and weak. The following table shows the estimated quarterly profits (in thousands of dollars): Service Demand for Service Strong WeakFull Price $960 -$490 Discount $670 $320 a. What is the decision to be made, what is the chance event, and what is the consequence for this problem? How many decision alternatives are there? How many outcomes are there for the chance event? - Decision to be Made: Myrtle Air Express is trying to decide whether to sell plane tickets at full or at a discounted price. - Chance Event: The demand is the chance event. - Consequence: Profit will either increase or decrease based on the strength of the demand. - There are four different outcomes for the chance event. The chance even is the level of demand for Myrtle air service. The consequence is the amount of quarterly profit. There are two decision alternatives which are fill price and discount price services. The number of outcomes for chance event is 2, which are strong demand and weak demand b. If nothing is known about the probabilities of the chance outcomes, what is the recommended decision using the optimistic, conservative, and mini-max regret approaches? Opportunistic – Full Price Conservative – Discount Mini-max Regret – Discount Optimistic Approach: Full price service Conservative Approach: Discount services Opportunity loss/regret table: High Demand Low Demand Maximum Regret Full Service 0 490+350=840 840 Discount Service 960-710=250 0 250 Discount service minimizes the maximum regret. c. Suppose that management of Myrtle Air Express believes that the probability of strong demand is and the probability of weak demand is 0.3. Use the expected value approach to determine an optimal decision.Expected Value: Full Price EV =( $ 960∗.30)+(−$ 490∗.30)=$ 141 Discount EV =($ 670∗.30)+( $320∗.30)=$ 297 The optimal decision would be to use the discounted price. d. Suppose that the probability of strong demand is 0.8 and the probability of weak demand is 0.2. What is the optimal decision using the expected value approach? Full Price EV =( $ 960∗.80)+(−$ 490∗.20)=$ 670 Discount EV =( $ 670∗.80)+( $ 320∗.20 )=$ 600 11. For the Pittsburgh Development Corporation problem in Section 4.3, the decision alternative to build the large condominium complex was found to be optimal using the expected value approach. In Section 4.4 we conducted a sensitivity analysis for the payoffs associated with this decision alternative. We found that the large complex remained optimal as long as the payoff for the strong demand was greater than or equal to $17.5 million and as long as the payoff for the weak demand was greater than or equal to -$19 million. a. Consider the medium complex decision. How much could the payoff under strong demand increase and still keep decision alternative d3 the optimal solution? EV d2 = .8 (s) + .2 (5) <_ 14.2 .8 (s)+1<_ 14.2 .8s<_ 14.2-1 .8s<_13.2 S<_13.2/.8 S<_16.5 The Payoff for the medium complex under strong demand is lesser than or equal to 16.5. The large complex under strong demand is the best alternative b. Consider the small complex decision. How much could the payoff under strong demand increase and keep decision alternative d3 the optimal solution? EV d2 = .8 (s) + .2 (7) <_ 14.2.8 (s)+1.4<_ 14.2 .8s<_ 14.2-1.4 .8s<_12.8 S<_12.8/.8 S<_16 The Payoff f medium for the small complex under strong demand is lesser than or equal to 16. The large complex under strong demand is the best alternative 13. Seneca Hill Winery recently purchased land for the purpose of establishing a new vineyard. Management is considering two varieties of white grapes for the new vineyard: Chardonnay and Riesling. The Chardonnay grapes would be used to produce a dry Chardonnay wine, and the Riesling grapes would be used to produce a semidry Riesling wine. It takes approximately four years from the time of planting before new grapes can be harvested. This length of time creates a great deal of uncertainty concerning future demand and makes the decision about the type of grapes to plant difficult. Three possibilities are being considered: Chardonnay grapes only; Riesling grapes only; and both Chardonnay and Riesling grapes. Seneca management decided that for planning purposes it would be adequate to consider only two demand possibilities for each type of wine: strong or weak. With of some forecasting in industry publications, management made the following probability assessments: Riesling Demand Chardonnay Demand Strong Weak Strong .05 .50 Weak .25 .20 Revenue projections show an annual contribution to profit of $20,000 in Seneca Hill only plants Chardonnay grapes and demand is weak for Chardonnay wine, and $70,000 if Seneca Hill only plants Chardonnay grapes and demand is strong for Chardonnay wine. If Seneca Hill only plants Riesling grapes, the annual profit projection is $25,000 if demand is weak for Riesling wine, and $45,000 if demand is strong for Riesling wine. If Seneca plants both types of grapes, the annual profit projections are shown in the following table: Riesling Demand Chardonnay Demand Strong Weak Strong $22,000 $40,000 Weak $26,000 $60,000a. What is the decision to be made, what is the chance event, and what is the consequence? Identify the alternatives for the decisions and possible outcomes for the chance even? The decision to be made: Type of grape or grapes to plant in order to maximize profit. Chance Event: Demand for the wine. (weak or strong) Consequences: Expected Annual Profit Contribution Decision Alternatives: Planting C type grapes only Planting R type grapes only Planting both types of grapes Chance outcomes: Weak demand for C type grapes, weak demand for R type grapes Weak demand for C type grapes, strong demand for R type grapes Strong demand for C type grapes, weak demand for R type grapes Strong demand for C type grapes, Strong demand for R type grapes b. Develop a Decision tree. I do not know how to make this in excel or word c. Using the expected value approach to recommend which alternative Seneca Hill Winery should following order to maximize expected annual profit. Expected Value(Chardonnay)=.55( $ 20,000)+.45 ( $ 70,000) ¿ 11,000+31,500 ¿$ 42,500 Expected Value(Both)=.05 ($ 22)+.50 ($ 40)+.25 ($ 26)+.20($ 60) ¿$ 39,600 Expected Value( Both)=.30 ( $ 25)+.70 ( $ 45 )¿$ 39,000 d. Suppose management is concerned about the probability assessments when demand for Chardonnay wine is strong. Some believe it is likely got Riesling demand to also be strong in this case. Suppose the probability of strong demand for Chardonnay and weak demand for Riesling is .05 and that the probability for strong demand for Chardonnay and strong demand for Riesling is .40. How does this change the recommended decision? Assume that the probabilities when Chardonnay demand is weak are still .05 and .50. Expected Value ( Both)=.05 ( $ 22)+.50 ($ 40)+.05 ($ 26)+.40 ($ 60) ¿$ 46,400 Expected Value( Riesling )=.10 ($ 25)+.90 ($ 45) ¿$ 43,000 e. Other members of the management team expect the Chardonnay market to become saturated at some point in the future, causing fall in prices. Suppose that eh annual profit projections fall to $50,000 when the demand for Chardonnay is strong and Chardonnay grapes only are planted. Using the original probability assessments, determine how this change would affect the optimal decision. Expected Value(Chardonnay )=.55( $ 50,000)+.45($ 70,000) ¿ 27,500+31,500 ¿$ 59,000 14. The following payoff table was presented in Problem 1: Decision Alternative State of Nature s 1 s2 s3 d1 250 100 25 d2 100 100 75 The probabilities for the states of nature are: P(s1)=0.65 P( s2)=0.15 P( s3)=0.20 a. What is the optimal decision strategy if perfect information were available?The first decision alternative would be the optimal decision. b. What is the expected value for the decision strategy developed is part (a)? EV ( d 1)=(250∗.65)+(100∗.15)+(25∗.20)=182.5 c. Using the expected value approach, what is the recommended decision without perfect information? What is the expected value? EV ( d 1)=(250∗.65)+(100∗.15)+(25∗.20)=182.5 EV ( d 2)=(100∗.65)+(100∗.15)+(75∗.20)=95 Decision 1 is recommended. d. What is the expected value of perfect information? EV (new )=(250∗.65)+(100∗.15)+(75∗.20 )=¿ EVPI=192.5 182.5=10 15 (1). The Lake Placid Town Council has decided to build a new community center to be used for conventions, concerts, and other public events, but considerable controversy surrounds the appropriate size. Many influential citizens want a large center that would be a showcase for the area, but the mayor feels that if demand does not support such a center, the community will lose a large amount of money. To provide structure for the decision process, the council narrowed the building alternatives to three sizes: small, medium, and large. Everybody agreed that the critical factor in choosing the best size is the number of people who will want to use the new facility. A Regional planning consultant provided demand estimate under three scenarios: worst case, base case, and best case. The worst-case scenario corresponds to a situation in which tourism drops significantly; the base-case scenario corresponds to a situation in which Lake Placid continues to attract visitors at current levels; and the best-case scenario corresponds to a significant increase in tourism. The consultant has provided probability assessments of .10, 60, and .30 for the worstcase, base-case, and best-case scenarios, respectively. The town council suggested using net cash flow over a five-year planning horizon as the criterion for deciding on the best size. A Consultant developed the following projections of net cash flow (in thousands of dollars) for a five-year planning horizon. All costs, including the consultant’s fee, are included.a. What decision should Lake Placid make using the expected value approach? Small = (0.1)400 + (0.6)500 + (0.3)660 = 538 Medium = (0.1)-250 + (0.6)650 + (0.3)800 = 605 Large = (0.1)-400 + (0.6)580 + (0.3)990 = 605 Since both the medium and large sized centers have the same EV, either or could be chosen for this scenario. b. Construct risk profiles for the medium and large alternatives. Given the mayor’s concern over the possibility of losing money and the result of part (a), which alternative would you recommend? Scenario of Medium Center A P AEV P(X) = (A – EV^2) Worst - 250 0. 1 -855 73,102.50 Base 650 0. 6 45 1215 Best 800 0. 3 195 11,407.50 Variance 85,725 Scenario of Large Center A P A-EV P(X) = (A – EV^2) Worst - 400 0. 1 - 1,005 101,002.50 Base 580 0. 6 -25 375 Best 990 0. 3 385 44,467.50 Variance 145,845 Risk of medium = 85,725 ^ 0.5 = 292.79. Risk of large = 145,845^0.5 = 381.90 With assessing the risk profiles, I would recommend the medium sized center. c. Compute the expected value of perfect information. Do you think it would be worth trying to obtain additional information concerning which scenario is likely to occur? Size of Center Maximu m P EVSmall 400 0. 1 40 Medium 650 0. 6 39 0 Large 990 0. 3 29 7 EV With PI 72 7 After finding the EV with PI, 727, you then subtract the EV without PI, 605, for a total of 122 for the EV of PI. To pursue additional information would benefit the city since it would possibly increase its net cash flow up $122,000. d. Suppose the probability of the worst-case scenario increases to 0.2, the probability of the basecases scenario decreases to 0.5, and the probability of the best-case scenario remains at 0.3. What effect, if any, would these changes have on the decision recommendation? Size of Center Worst + Base + Best = EV Small 0.2(400) 0.5(500 ) 0.3(660 ) 528 Medium 0.2(- 250) 0.5(650 ) 0.3(800 ) 515 Large 0.2(- 400) 0.5(580 ) 0.3(990 ) 507 I would recommend the small sized center based of an EV of 528. e. The consultant has suggested that an expenditure of $150,000 on a promotional campaign over the planning horizon will effectively reduce the probability of the worst-case scenario to zero. If the campaign can be expected to also increase the probability of the best-case scenario to 0.4, is it a good investment? Size of Center Worst + Base + Best = EV Small 0(400) 0.6(500 ) 0.4(660 ) 564 Medium 0(- 250) 0.6(650 ) 0.4(800 ) 710 Large 0(- 400) 0.6(580 ) 0.4(990 ) 744I would recommend building the large center even though its EV is less than the EV of the medium center without the promotion. Using the campaign would reduce the net cash flow of all of these centers but since the mayor is concerned about the risk of losing money, possibly affecting their re-election, this route would be more favorable to them to eliminate risks. 15 (2). The Lake Placid Town Council has decided to build a new community center to be used for conventions, concerts, and other public events, but considerable controversy surrounds the appropriate size. Many influential citizens want a large center that would be a showcase for the area, but the mayor feels that if demand does not support such a center, the community will lose a large amount of money. To provide structure for the decision process, the council narrowed the building alternatives to three sizes: small, medium, and large. Everybody agreed that the critical factor in choosing the best size is the number of people who will want to use the new facility. A Regional planning consultant provided demand estimate under three scenarios: worst case, base case, and best case. The worst-case scenario corresponds to a situation in which tourism drops significantly; the base-case scenario corresponds to a situation in which Lake Placid continues to attract visitors at current levels; and the best-case scenario corresponds to a significant increase in tourism. The consultant has provided probability assessments of . 10, 60, and .30 for the worst-case, base-case, and best-case scenarios, respectively. The town council suggested using net cash flow over a five-year planning horizon as the criterion for deciding on the best size. A Consultant developed the following projections of net cash flow (in thousands of dollars) for a five-year planning horizon. All costs, including the consultant’s fee, are included. a. What decision should Lake Placid make using the expected value approach? Small = (0.1)400 + (0.6)500 + (0.3)660 = 538 Medium = (0.1)-250 + (0.6)650 + (0.3)800 = 605 Large = (0.1)-400 + (0.6)580 + (0.3)990 = 605 Since both the medium and large sized centers have the same EV, either or could be chosen for this scenario. b. Construct risk profiles for the medium and large alternatives. Given the mayor’s concern over the possibility of losing money and the result of part (a), which alternative would you recommend? Scenario of Medium Center A A-EV P(X) = (A – EV^2) Worst -250 -855 73,102.50Base 650 45 1215 Best 800 195 11,407.50 Variance 85,725 Scenario of Large Center A A-EV P(X) = (A – EV^2) Worst -400 -1,005 101,002.50 Base 580 -25 375 Best 990 385 44,467.50 Variance 145,845 Risk of medium = 85,725 ^ 0.5 = 292.79. Risk of large = 145,845^0.5 = 381.90 With assessing the risk profiles, I would recommend the medium sized center. c. Compute the expected value of perfect information. Do you think it would be worth trying to obtain additional information concerning which scenario is likely to occur? Size of Center Maximu m Small 400 Medium 650 Large 990 EV With PI After finding the EV with PI, 727, you then subtract the EV without PI, 605, for a total of 122 for the EV of PI. To pursue additional information would benefit the city since it would possibly increase its net cash flow up $122,000. d. Suppose the probability of the worst-case scenario increases to 0.2, the probability of the basecases scenario decreases to 0.5, and the probability of the best-case scenario remains at 0.3. What effect, if any, would these changes have on the decision recommendation? Size of Center Worst + Base + Best = EV Small 0.2(400) 0.5(500) 0.3(660) 528 Medium 0.2(-250) 0.5(650) 0.3(800) 515 Large 0.2(-400) 0.5(580) 0.3(990) 507 I would recommend the small sized center based of an EV of 528. e. The consultant has suggested that an expenditure of $150,000 on a promotional campaign over the planning horizon will effectively reduce the probability of the worst-case scenario tozero. If the campaign can be expected to also increase the probability of the best-case scenario to 0.4, is it a good investment? Size of Center Worst + Base + Best = EV Small 0(400) 0.6(500) 0.4(660) 564 Medium 0(-250) 0.6(650) 0.4(800) 710 Large 0(-400) 0.6(580) 0.4(990) 744 I would recommend building the large center even though its EV is less than the EV of the medium center without the promotion. Using the campaign would reduce the net cash flow of all of these centers but since the mayor is concerned about the risk of losing money, possibly affecting their re-election, this route would be more favorable to them to eliminate risks. 19. Hales TV Production is considering producing a pilot for a comedy series in the hope of selling it to a major television network. The network may decide to reject the series, but it may also decide to purchase the rights to the series for either one year or two year. At this point in time, Hale may either produce the series and wait for the networks decision or transfer the rights of the pilot and series to a competitor for $100,000. Hales decision alternatives and profits (in thousands of dollars) are as follows: State of Nature Decision Alternative Reject s1 1 Year s2 2 Years s3 Produce Pilot D1 - 100 50 150 Sell to competitor D2 100 100 100 Probabilities for the states of nature are P (S1) = 0.20, P (S2) = 0.30, and P (S3) = 0.50. For a consulting fee of $5,000, an agency will review the plans for the comedy series and indicate the overall chances of a favorable network reaction to the series. Assume that the agency review will result in a favorable (F) or unfavorable (U) review and that the following probabilities are relevant: P (F) = 0.69 P (U) = 0.31 P (S1|F) = 0.09 P (S1| U) = 0.45 a. Construct a decision tree for this problem. P (S2|F) = 0.26 P (S2|U) = 0.39 P (S3|F) = 0.65 P (S3|U) = 0.16b. What is the recommended decision if the agency opinion is not used? What is the expected value? EV (D1) = 0.20(-100) + 0.30(50) + 0.50(150) = 70 EV (D2) = 0.20(100) + 0.30(100) + 0.50(100) = 100 I would recommend D2 since its EV is $100,000. c. What is the expected value of perfect information? EV with PI = 0.20(100) + 0.30(100) + 0.50(150) = 125 – 100 = $25,000 d. What is Hale’s optimal decision strategy assuming the agency’s information is used? EV (D1|F) = 0.09(-100) + 0.26(50) + 0.65(150) = 101.5 EV (D2|F) = 0.09(100) + 0.26(100) + 0.65(150) = 100 EV (D1|U) = 0.45(-100) + 0.39(50) + 0.16(150) = -1.5 EV (D2|U) = 0.45(100) + 0.39(100) + 0.16(100) = 100 The optimal decision would be to sell the rights of the pilot if there is a favorable reaction. S1 $-100,000 Favorable Hire an agency S2 $50,000 S3 $150,000 S1 $100,000 S2 $100,000 S3 $100,000 S1 $-100,000 Not favorable Sell or produce S2 $50,000 S3 $150,000 S1 $100,000 D2 S2 $100,000 S1 $-100,000 S3 $100,000 D1 Don't hire agency D2 S2 $50,000 S3 $150,000 S1 $100,000 S2 $100,000 S3 $100,000 D1 D2 D1e. What is the expected value of the agency’s information? EV = 0.69(101.5) + 0.31(100) = 101.035 – 100 = $1,035 f. Is the agency’s information worth the $5,000 fee? What is the maximum that Hale should be willing to pay for the information? The information is not worth the consultation fee since their EV is only $5,000. g. What is the recommended decision? I would recommend that Hale should not hire the agency since the information they would provide is less than what they charge for the service and sell the rights for $100,000. 21. A real estate investor has the opportunity to purchase land currently zoned residential. If the county board approves a request to rezone the property as commercial within the next year, the investor will be able to lease the land to a large discount firm that wants to open a new store on the property. However, if the zoning change is not approved, the investor will have to sell the property at a loss. Profits (in thousands of dollars) are shown in the following payoff table: State of Nature Decision Alternative Rezoning Approved, S1 Rezoning Not Approved, S2 Purchase, D1 600 - 200 Do not purchase, D2 0 0 a. If the probability that the rezoning will be approved is 0.5, what decision is recommended? What is the expected profit? EV (D1) = 0.5(600) + 0.5(-200) = 200,000. $200,000 is enough profit to move forward with the decision. b. The investor can purchase the land anytime during the next three months while learning more about possible resistance to the rezoning proposal from area residents. What is the optimal decision strategy if the investor uses the option period to learn more about the resistance from area residents before making the purchase known? Use H = high resistance and L = to low resistance to zoning. P (H) = 0.55 P (L) = 0.45 P (S1|H) = 0.18 P (S1|L) = 0.89 P (S2|H) = 0.82 P (S2|L) = 0.11EV (D1|H) = 600(0.18) + -200(0.82) = -56,000 EV (D1|L) = 600(0.89) + -200(0.11) = 512,000 EV with option = 512,000(0.45) = $230,400 The apparent optimal decision here would be to go with the option and buy if the resistance is to rezoning. c. If the option will cost the investor an additional $10,000, should the investor purchase the option? Why or why not? What is the maximum that the investor should be willing to pay for the option? Even with an additional ten grand in cost, the EV would still be more than not purchasing the option so the maximum the investor should be willing to pay is $20,400. 23. Suppose that you are given a decision situation with three possible states of nature: S1, S2, and S3. The prior probabilities are P(S1) = 0.18, P(S2) = 0.48, and P(S3) = 0.34. With sample information I, P(I | S1) = 0.10, P(I | S2) = 0.04, and P(I | S3) = 0.22. Compute the revised or posterior probabilities: P(S1 | I), P(S2 | I), and P(S3 | I). If required, round your answers to four decimal places. Explanation: We have: P(S1) = 0.18, P(S2) = 0.48, and P(S3) = 0.34 P(I | S1) = 0.10, P(I | S2) = 0.04, and P(I | S3) = 0.22 They ask us: a) p(S1/l) =? Applying the bayes theorem, we have: p(S1/l) =p(l)p(l/S1)/p(S1) Where, applying the total probability theorem, we have: p(l)=pl/S1)p(S1)+p(l/S2)p(S2)+p(l/S3)p(S3) p(l)=0.10(0.18) +0.04(0.48) +0.22(0.34) .018+.0192+.0748=.112 Therefore: p(S1/l) = .018/.112=.1607 b) p(S2/l)=p(l)p(l/S2)p(S2)/ p(l) =..0192/.112= .1714 c) p(S3/l)=p(l)p(l/S3)p(S3) p(l) = .0748/.112= .6678s s LowDDDeeemmmaaannnddd -20 Manufacture MediumDDDeeemmmaaannnddd 40 HighDDDeeemmmaaannnddd 100 Gorman Manufactuuurrriiinnnggg Company LowDDDeeemmmaaannnddd 10 Purchase MediumDDDeeemmmaaannnddd 45 HighDDDeeemmmaaannnddd 70 25. The Gorman Manufacturing Company must decide whether to manufacture a component part at its Milan, Michigan, plant or purchase the component part from a supplier. The resulting profit is dependent upon the demand for the product. The following payoff table shows the projected profit (in thousands of dollars): Decision State of Nature Low Demand Medium Demand High Demand Alternative 1 2 3 Manufacture, d 1 -20 40 100 Purchase, d2 10 45 70 The state-of-nature probabilities are: P(s1)=0.35 P( s2)=0.35 P( s3)=0.30 a. Use a decision tree to recommend a decision. I would choose the purchase decision because, even though it doesn’t yield as much profit, the worst outcome will still produce a marginal profit. EV (D1) = 0.35(-20) + 0.35(40) + 0.30(70) = 37 sEV (D2) = 0.35(10) + 0.35(45) + 0.30(70) = 40.25 I would recommend decision D2 with an EV of $40,250. b. Use EVPI to determine whether Gorman should attempt to obtain a better estimate of demand. ER(new)=(10∗.35)+(45∗.35 )+(100∗.30 )=49.25 EVPI=49.25−40.25=9 It might be more beneficial for Gorman to attempt to obtain a better estimate of demand. Profits may be boosted by $9,000 from obtaining a better estimate of demand; pending cost of acquiring such data. c. A test market study of the potential demand for the product is expected to report either a favorable (F) or unfavorable (U) condition. The relevant conditional probabilities are as follows: P(F∣s1)=0.10 P(U∣s1)=0.90 P(F∣s2)=0.40 P(U∣s2)=0.60 P(F∣s3)=0.60 P(U∣s3)=0.40 What is the probability that the market research report will be favorable? Prob of Fav .=(.35∗.10)+(.35∗.40)+(.30∗.60)=35.5 % Probof Fav.=.031+.14 +18=.355 Event s Prior Prob. Con. Prob. Joint Prob. Post. Prob. S1 P(S1) P(F|S1) P(S1∩F) P(S1/F) S1 0.35 0.10 0.035 ≈ 0.099 S2 0.35 0.40 0.140 ≈ 0.394 S3 0.30 0.60 0.180 ≈ 0.507 Totals 1.00 P(F) = 0.355 1.000 Event s Prior Prob. Con. Prob. Joint Prob. Post. Prob. S1 P(S1) P(U|S1) P(S1∩U) P(S1/U) S1 0.35 0.90 0.315 ≈ 0.488S2 0.35 0.60 0.210 ≈ 0.326 S3 0.30 0.40 0.120 ≈ 0.186 Totals 1.00 P(U) = 0.645 1.000 d. What is Gorman’s optimal decision strategy? Gorman’s optimal decision strategy is state of nature 3. EV (D1|F) = 0.099(-20) + 0.394(40) + 0.507(100) = 64.48 EV (D2|F) = 0.099(10) + 0.394(45) + 0.507(70) = 54.21 EV (D1|U) = 0.488(-20) + 0.326(40) + 0.186(00) = 21.88 EV (D2|U) = 0.488(10) + 0.326(45) + 0.186(70) = 32.57 EV with Research = 0.355(64.48) + 0.645(32.57) = 43.89805 With this being determined, the research should be used. If the market is favorable the component should be manufactured by Gorman’s. If the market is unfavorable the component Gorman’s should purchase the component. e. What is the expected value of the market research information? EVSI=(−20∗.031)+( 40∗.14 )+(100∗.18 )=22.98 EVSI=(10∗.031)+(45∗.14 )+ (70∗.18 )=19.21 EV (Research) = 43.89805 – 40.25 = 3.64805 = $3,648 f. What is the efficiency of the information? Efficiency=3.77 =.418�41.8 % 3% [Show More]

Last updated: 2 years ago

Preview 1 out of 21 pages