Finance > Solutions Guide > Solutions June 2015 paper 2 (AS1051 (All)

Solutions June 2015 paper 2 (AS1051

Document Content and Description Below

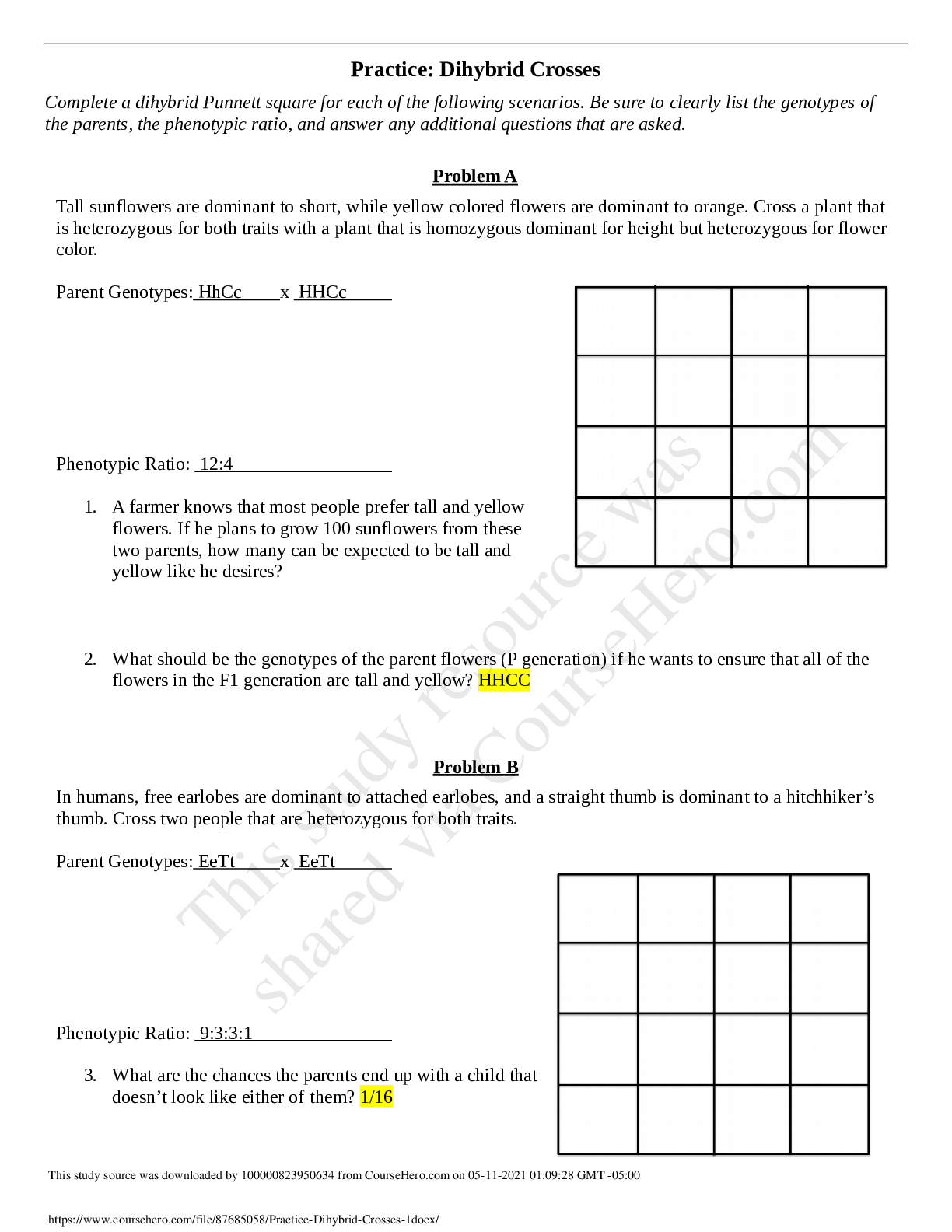
Solutions June 2015 paper 2 (AS1051) Section A 1. (a) (seen in sample class test) i. y is an upper bound for A precisely when 8a 2 A; a ≤ y. 2 ii. u is the least upper bound of A precisely when ... u is an upper bound of A, and for any y another upper bound of A, we have u ≤ y. 2 (b) (unseen) In the interval X we have cos(x) > 1=p2 precisely when −π=4 < x < π=4. The least upper bound of A is therefore π=4. 4 2. (unseen) Using the auxiliary equation λ2 − 5λ + 4 = (λ − 4)(λ − 1) we determine that the solution for the homogeneous equation is A n = 4nA + B: Now we can try An = a7n, substituting we get 3 (a7n+2) − 5(a7n+1) + 4(a7n) = 7n a(72 − 5 × 7 Section A 1. (a) (seen in sample class test) i. y is an upper bound for A precisely when 8a 2 A; a ≤ y. 2 ii. u is the least upper bound of A precisely when u is an upper bound of A, and for any y another upper bound of A, we have u ≤ y. 2 (b) (unseen) In the interval X we have cos(x) > 1=p2 precisely when −π=4 < x < π=4. The least upper bound of A is therefore π=4. 4 2. (unseen) Using the auxiliary equation λ2 − 5λ + 4 = (λ − 4)(λ − 1) we determine that the solution for the homogeneous equation is A n = 4nA + B: Now we can try An = a7n, substituting we get 3 (a7n+2) − 5(a7n+1) + 4(a7n) = 7n a(72 − 5 × 7 [Show More]

Last updated: 3 years ago

Preview 1 out of 7 pages

Buy Now

Instant download

We Accept: