
BCOM (Business Communication) 11th Edition By Carol Lehman, Debbie DuFrene, Robyn Walker (Test Bank All Chapters, 100% Original Verified, A+ Grade)
$ 25

Chamberlain College of Nursing NR 283 NR 283 SYLLABUS.






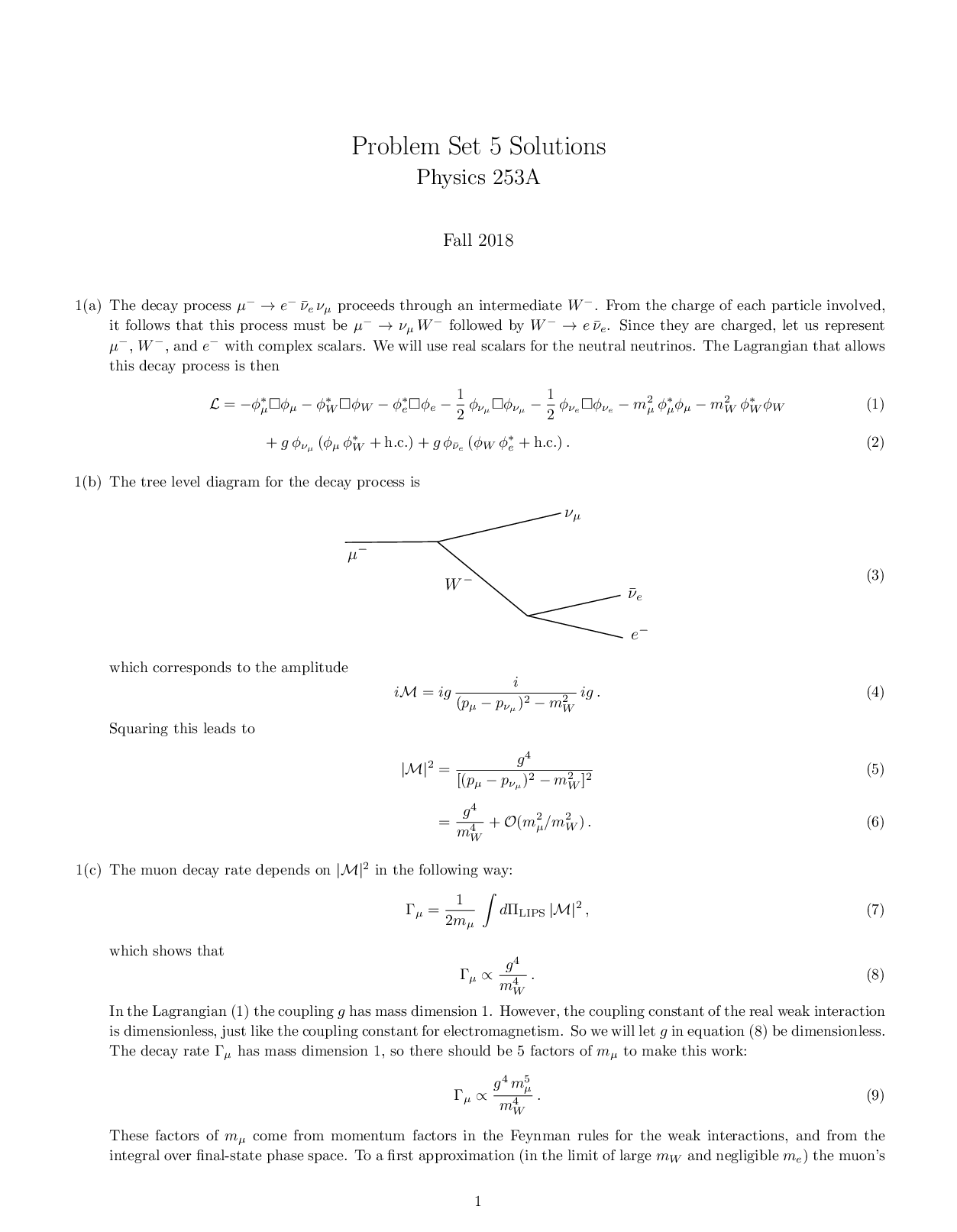

 University of Cambridge Local Examinations Syndicate - Cambridge IELTS 3 Student's Book with Answers_ Examination Papers from the University of Cambridge Local Examinations Synd.png)
.png)
.png)
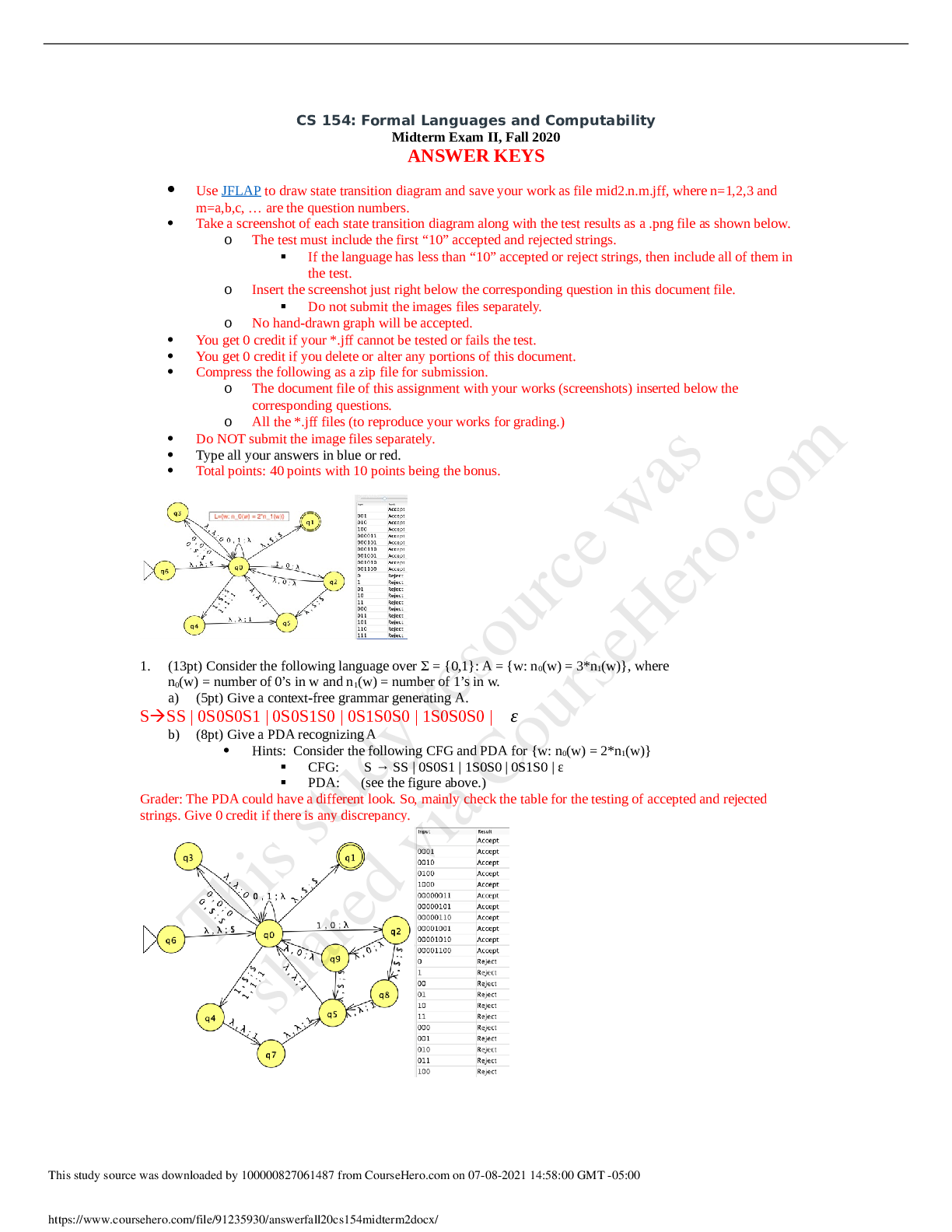

.png)





 V1-V2.png)




.png)


