Mathematics > Solutions Guide > Linear Algebra: Concepts and Methods Solutions to Problems Martin Anthony and Michele Harvey Departm (All)
Linear Algebra: Concepts and Methods Solutions to Problems Martin Anthony and Michele Harvey Department of Mathematics The London School of Economics and Political Science
Document Content and Description Below
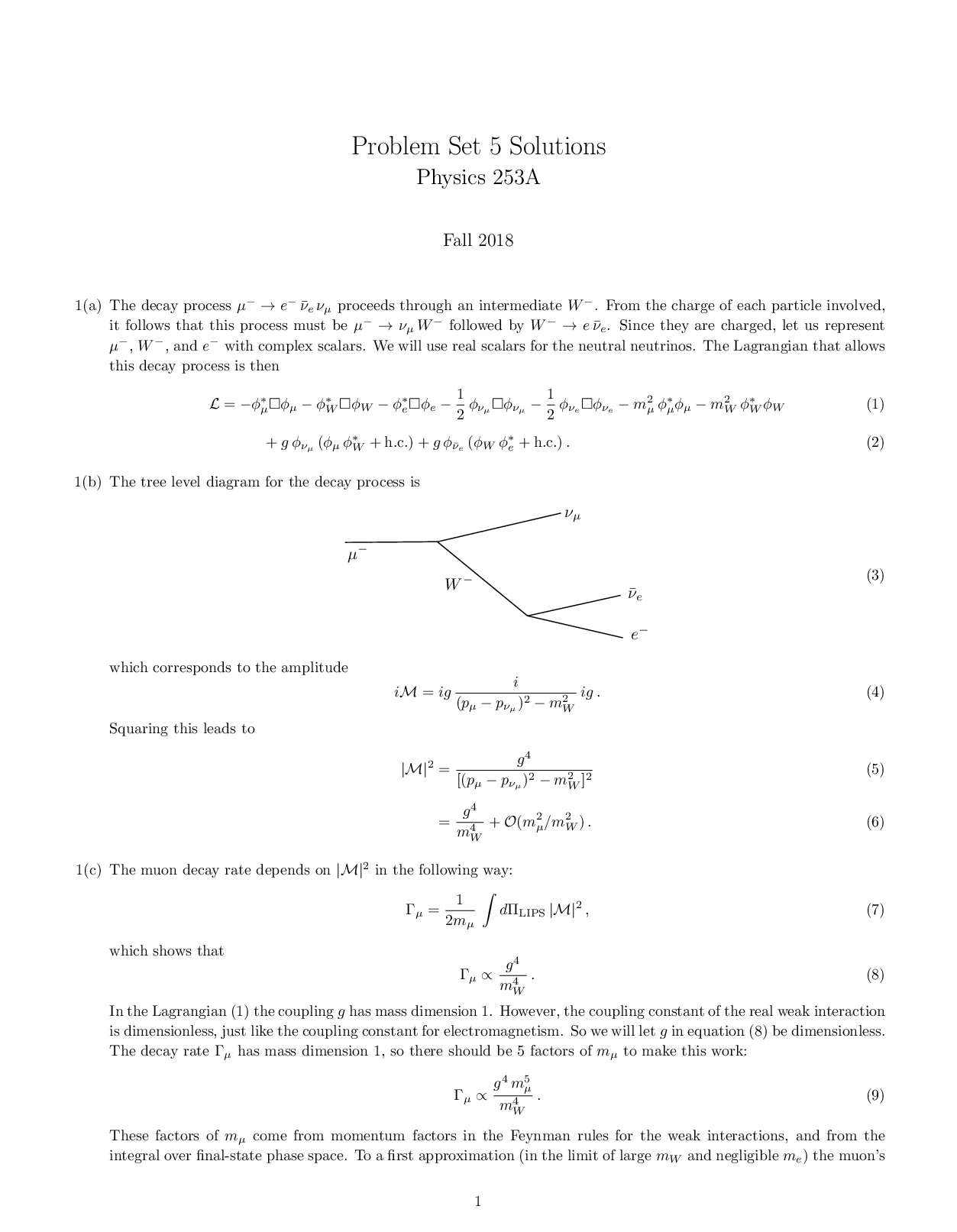
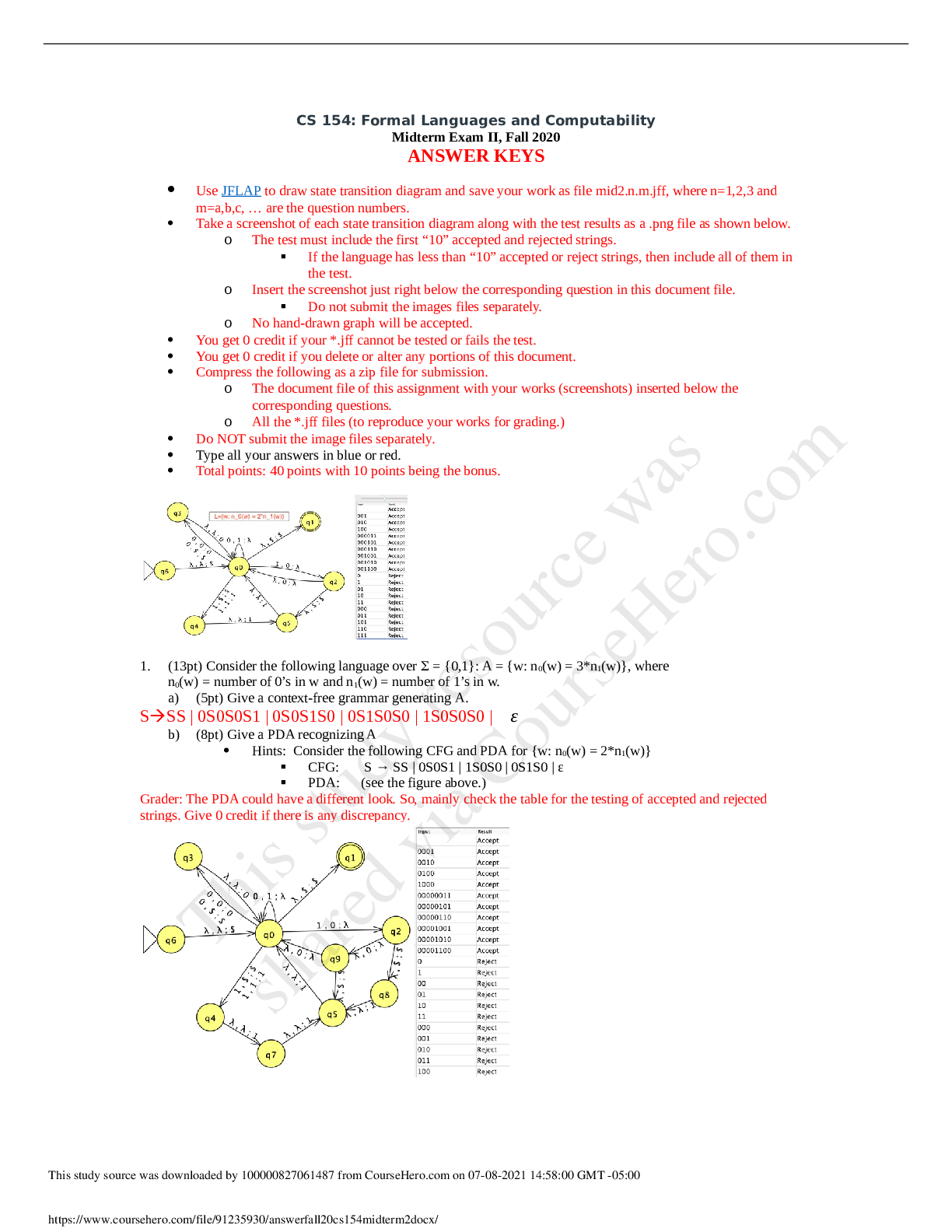
Linear Algebra: Concepts and Methods Solutions to Problems Martin Anthony and Michele Harvey Department of Mathematics The London School of Economics and Political Science2Introduction This docum ... ent contains solutions to all the Problems from the book ‘Linear Algebra: Concepts and Methods’. It is intended as an aid to those who use the text in support of teaching a course in linear algebra. 34Chapter 1 Problem 1.1 (a) Ab is not defined. (b) Since C is a 3 × 3 matrix and A is 3 × 2, the product CA is defined and is the 3 × 2 matrix CA = 1 2 1 3 0 4 1 1 −1 2 1 1 1 0 3 = 4 6 6 0 9 8 (c) A + Cb is not defined, since Cb is 3 × 1 and A is 3 × 2. (d) A + D = 2 2 3 6 6 6 (e) bTD = ( 1 1 −1 ) 0 1 2 5 6 3 = ( −4 3 ) (f) The product DAT is a 3 × 3 matrix, as is C, so this expression is defined: DAT = 0 1 2 5 6 3 ( 2 1 0 1 1 3 ) = 15 9 9 1 1 3 9 7 15 , 56 CHAPTER 1. DAT + C = 15 9 9 1 1 3 9 7 15 + 1 2 1 3 0 4 1 1 −1 = 12 7 14 19 10 10 2 3 4 (g) bTb = ( 1 1 −1 ) −1 11 = (3). As mentioned in Section 1.8.2, we normally just identify a 1 × 1 matrix by its entry. So we may write (3) as 3. (h) bbT = −1 11 ( 1 1 −1 ) = −1 1 1 1 1 −1 1 − −1 1 (i) Cb = 1 2 1 3 0 4 1 1 −1 −1 11 = 2 4 4 Problem 1.2 The matrix aTb is the product of a 1 × n matrix and an n × 1 matrix, so it is a 1 × 1 matrix (which can be identified with the scalar it represents; that is, the scalar given by the inner product ⟨a, b⟩ ). The product bTa is also a 1 × 1 matrix. Since the product aTb is a 1 × 1 matrix, it is symmetric, so that aTb = (aTb)T = bTa. Problem 1.3 We have [Show More]
Last updated: 3 years ago
Preview 1 out of 155 pages
.png)
Buy this document to get the full access instantly
Instant Download Access after purchase
Buy NowInstant download
We Accept:

Reviews( 0 )
$11.00
Can't find what you want? Try our AI powered Search
Document information
Connected school, study & course
About the document
Uploaded On
Jul 09, 2021
Number of pages
155
Written in
All
Additional information
This document has been written for:
Uploaded
Jul 09, 2021
Downloads
0
Views
154






 University of Cambridge Local Examinations Syndicate - Cambridge IELTS 3 Student's Book with Answers_ Examination Papers from the University of Cambridge Local Examinations Synd.png)
.png)

.png)





 V1-V2.png)




.png)

