MATH 310 Differential Equations Fall 2014
Midterm Exam
31 October 2014
Name: SFU ID: @sfu.ca
Tutorial Section: Student Number:
Question 1 2 3 4 5 6 Total
Marks
Instructions: Show all your work for full credit, and
...
MATH 310 Differential Equations Fall 2014
Midterm Exam
31 October 2014
Name: SFU ID: @sfu.ca
Tutorial Section: Student Number:
Question 1 2 3 4 5 6 Total
Marks
Instructions: Show all your work for full credit, and indicate your answers clearly.
There are six (6) questions, for a total of 50 points.
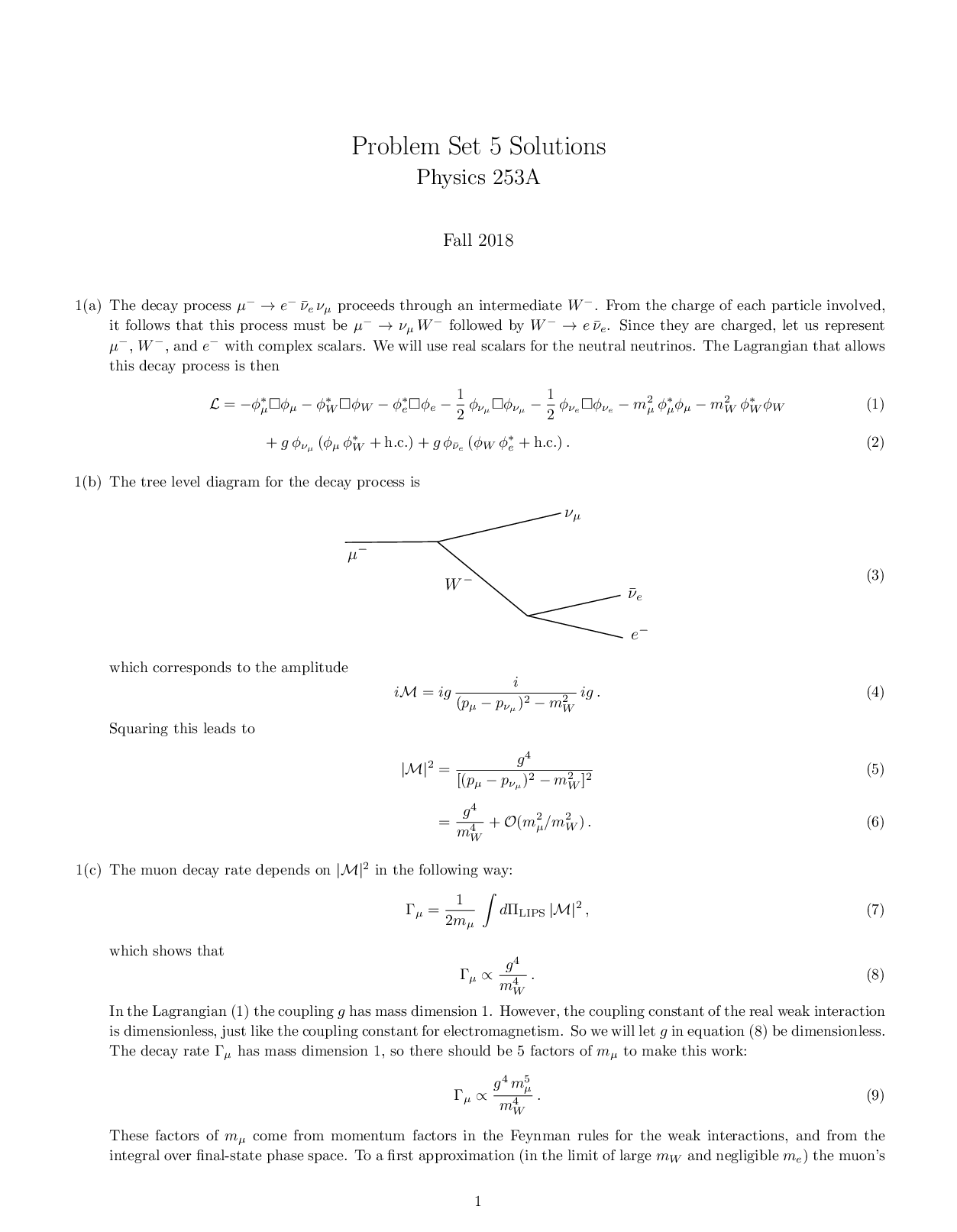
1. [8 points]
Consider the initial-value problem
(1 + x)dy
dx = y +
(1 + x)2
4 − 3x
; y(1) = −3:
Find the longest interval in which the solution to this problem is guaranteed to
exist.
Then find the solution y(x) of the initial-value problem, and check your solution by
substitution into the differential equation.
12. [8 points]
Consider the differential equation
x
dy
dx = y + x ey=x: (1)
(a) Show that using the substitution v = y=x, equation (1) reduces to the differential equation for v(x)
x
dv
dx = ev: (2)
(b) Find the general solution of equation (2), and hence solve the initial-value
problem
x
dy
dx = y + x ey=x; y(1) = −2
to find the solution y(x) explicitly. What is the maximal interval of existence
of the solution?
23. [10 points]
(a) A tank contains 100 litres (L) of water with 6 kg of salt dissolved in it. Pure
water is pumped in at 5 L/s, and the mixture is pumped out at the same rate.
How long will it take until there is 1 kg of salt in the tank?
(b) Consider the differential equation
dy
dt =
(y − 3)2=5
t2 :
For which of the following initial conditions can you say for sure (using the
Existence-Uniqueness Theorem) that there exists a solution of the corresponding initial-value problem?
If a solution is guaranteed to exist, for which initial conditions can you further
say for sure that it is the only one?
Justify your answers. [Do not attempt to solve the differential equation.]
(a) y(0) = 1; (b) y(1) = 2; (c) y(2) = 3:
34. [6 points]
Consider the autonomous differential equation (of the form y0 = f(y))
y0 = λ − y2
depending on a parameter λ.
For each of the following values of λ, find the critical points (if any) and determine
their stability; in addition, for the solution with y(0) = 0, sketch the solution curve
and determine the long-time behaviour limt!1 y(t) (without solving the ODE):
(a) λ = −1;
(b) λ = 1.
5. [6 points]
(a) Consider the constant-coefficient differential equation
y00 + by0 + cy = 0: (3)
Given that y1(t) = e2t and y2(t) = e−t are solutions of equation (3), find the
values of the constants b and c.
(b) For the values of b and c found in (a), solve the initial-value problem
y00 + by0 + cy = 0; y(0) = 6; y0(0) = β:
For which value(s) of β does the solution remain bounded as t ! +1?
46. [12 points]
(a) Verify that y1(x) = x1=2 is a solution of the linear homogeneous differential
equation
4x2y00 + y = 0; x > 0:
Use the method of reduction of order or Abel’s formula to find a second independent solution y2(x).
(b) Suppose that y1(t) and y2(t) are solutions of the linear homogeneous differential
equation
y00 + p(t)y0 + q(t)y = 0
on an interval I, where p(t) and q(t) are continuous on I.
If y1(t0) = 0 and y2(t0) = 0 for some t0 2 I, prove that y1 and y2 cannot be a
fundamental set of solutions on I.
(c) Find the general solution of
y(4) − 4y000 + 7y00 = 0:
5
[Show More]
.png)







 University of Cambridge Local Examinations Syndicate - Cambridge IELTS 3 Student's Book with Answers_ Examination Papers from the University of Cambridge Local Examinations Synd.png)
.png)

.png)








 V1-V2.png)




