Harvard UniversityPHYSICS 253APS5_253A_solutions

Problem Set 5 Solutions Physics 253A Fall 2018 1(a) The decay process µ− ! e− ν¯e νµ proceeds through an intermediate W −. From the charge of each particle involved, it follows that this process must be µ− ! νµ W − f ...

Problem Set 5 Solutions Physics 253A Fall 2018 1(a) The decay process µ− ! e− ν¯e νµ proceeds through an intermediate W −. From the charge of each particle involved, it follows that this process must be µ− ! νµ W − followed by W − ! e ν¯e. Since they are charged, let us represent µ−, W −, and e− with complex scalars. We will use real scalars for the neutral neutrinos. 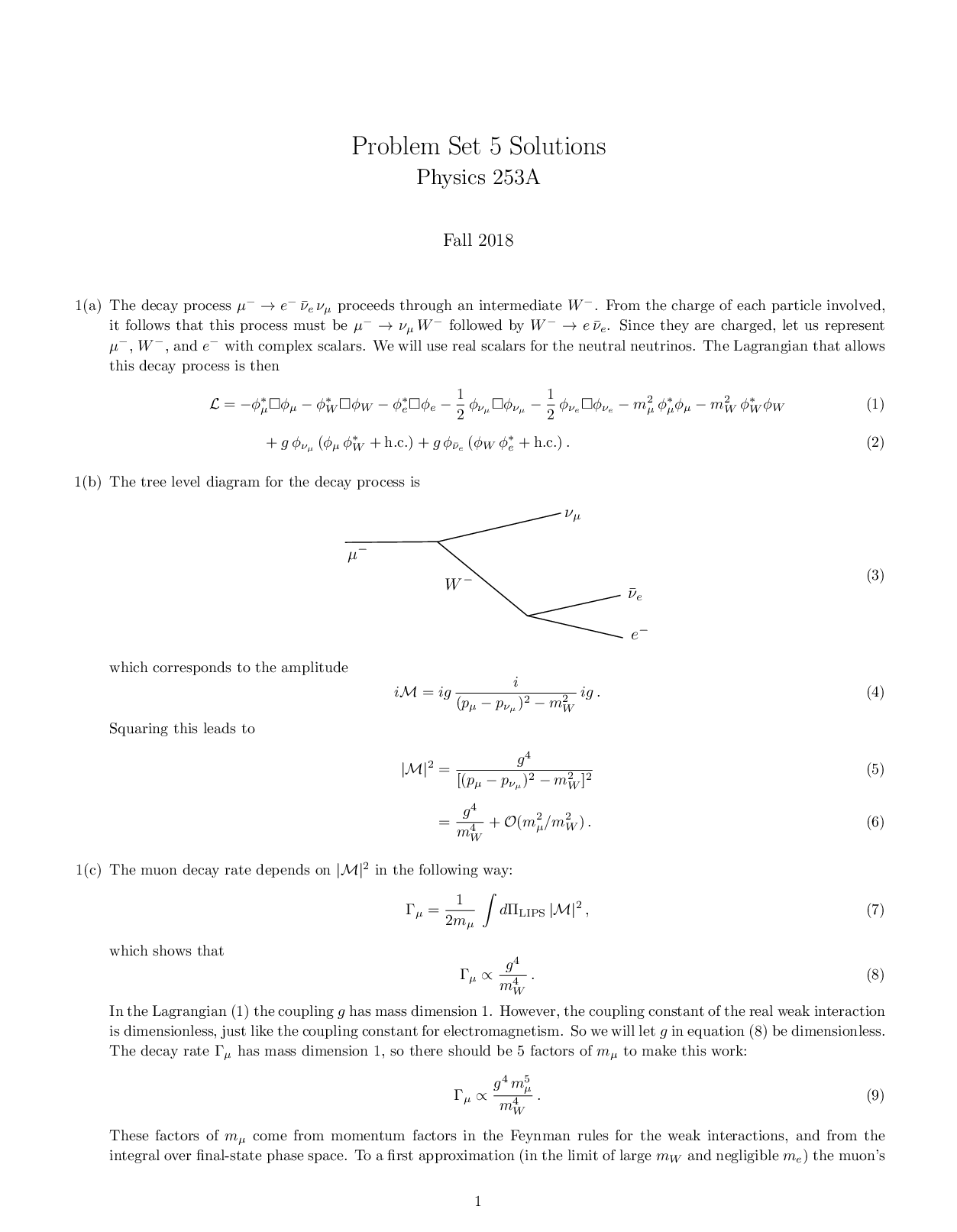The Lagrangian that allows this decay process is then L = −φ∗ µφµ − φ∗ W φW − φ∗ eφe − 1 2 φνµφνµ − 12 φνeφνe − m2 µ φ∗ µφµ − m2 W φ∗ W φW (1) + g φνµ (φµ φ∗ W + h.c.) + g φν¯e (φW φ∗ e + h.c.) : (2) 1(b) The tree level diagram for the decay process is µ! ! µ W ! e! !¯e (3) which corresponds to the amplitude iM = ig i (pµ − pνµ)2 − m2 W ig : (4) Squaring this leads to jMj2 = g4 [(pµ − pνµ)2 − m2 W ]2 (5) = g4 m4 W + O(m2 µ=m2 W ) : (6) 1(c) The muon decay rate depends on jMj2 in the following way: Γ µ = 1 2m µ Z dΠLIPS jMj2 ; (7) which shows that Γ µ / g4 m4 W : (8) In the Lagrangian (1) the coupling g has mass dimension 1. However, the coupling constant of the real weak interaction is dimensionless, just like the coupling constant for electromagnetism. So we will let g in equation (8) be dimensionless. The decay rate Γµ has mass dimension 1, so there should be 5 factors of mµ to make this work: Γ µ / g4 m5 µ m4 W : (9) These factors of m µ come from momentum factors in the Feynman rules for the weak interactions, and from the integral over final-state phase space. To a first approximation (in the limit of large mW and negligible me) the muon’s 1mass is the only dimensionful quantity controlling the momentum flowing through the legs of the diagram as well as the size of final-state phase space. This justifies the factor of m5 µ in equation (9). The integral over 3-body phase space also leads to a numerical factor of 1=192π3. This leads to Γ µ = g4 m5 µ 192π3 m4 W : (10) We arrived at this form by a direct calculation in Problem Set 3. 1(d) The muon has a mass of mµ = 105:7 MeV and lifetime of 2:197 microseconds. If we guess that g ∼ 1=137 as in electromagnetism, this leads to g ∼ 0:3. Working to a single significant figure, since we are hoping for an order-ofmagnitude estimate, we have ~ 2 × 10−6 sec ∼ (0:3)4 (100 MeV)5 192π3 m4 W ; (11) which implies mW ∼ 80 GeV: (12) 1(e) By applying the arguments above to the τ− ! e− ν¯e ντ decay, we can write Γτ!e ν¯e ντ = g4 m5 τ 192π3 m4 W : (13) If this were the only decay channel for the tau, we would have Γτ = m5 τ m5 µ Γ µ : (14) This would allow us to estimate mτ in terms of only Γτ, Γµ, and mµ; 1 3 × 10−13 sec ∼ m5 τ (100 MeV)5 1 2 × 10−6 sec ; (15) which would imply mτ ∼ 2 GeV: (16) 1(f) In reality, the tau decays to e− ν¯e ντ only 17.82% of the time, meaning that Γτ!e ν¯e ντ = 0:1782 Γτ : (17) The muon virtually always decays through this channel. Using this, we can get an accurate estimate of mτ from 0:1782 2:903 × 10−13 sec = m5 τ (105:7 MeV)5 1 2:197 × 10−6 sec : (18) We find mτ = 1:778 GeV ; (19) which is very close to the actual value. 1(g) In part (b) we approximated jMj2, keeping only the leading g4=m4 W dependence. The first subleading term is of the form g4 (pµ − pνµ)2=m6 W which is of relative order m2 µ=m2 W . The leading and subleading terms have different dependence on the momenta of the outoing particles. If one could very precisely measure the muon decay distribution, perhaps for example dΓ=dj~pej, then one could separately measure the leading term (with g4=m4 W ) and the subleading term (with g4=m6 W ), and thus separately measure g and mW . This would require precision at the m2 µ=m2 W ∼ 0:0002% level for the muon decay distribution, or the m2 τ=m2 W ∼ 0:05% level for the tau decay distribution. 2(a) With a propagator of the form i p2 − m2 + i m Γ ; Γ > 0 ; (20) 2the matrix element for s-channel 2 ! 2 scattering takes the form