The Luciferian Book

$ 2.5

IVY SOFTWARE BUSINESS MATH AND STATISTICS EXAM 2024 NEWEST COMPLETE 200 QUESTIONS AND CORRECT DETAILED ANSWERS (VERIFIED ANSWERS) ALREADY GRADED A+ BRAND NEW!!

$ 19

DAT 310 Data Analytics: Exercise 8-1 | Answered Spring 2025/2026.

$ 9

COMM 160 UNIT 3 Graded Assignment

$ 15

Foothill College - CS 6601Midterm 2.

$ 7

Cambridge International AS & A Level MATHEMATICS 9709/41 Paper 4 Mechanics 2022 + MARK SCHEME

$ 10

NREMT Practice Test Bank - Multiple Choice

$ 15

Nsg 6005 midterm.docx Graded A

$ 13.5

CARRIBEAN ADVANCED PROFICIENCY EXAMINATION® DIGITAL MEDIA – UNIT 1 Paper 01 | Download for quality grades |

$ 10

MUS 1013 Critical Essay B complete solution well stated essay

$ 8

Let's Communicate, 1e by Douglas Fraleigh, Joseph Tuman, Katherine Adams (Test Bank)

$ 25

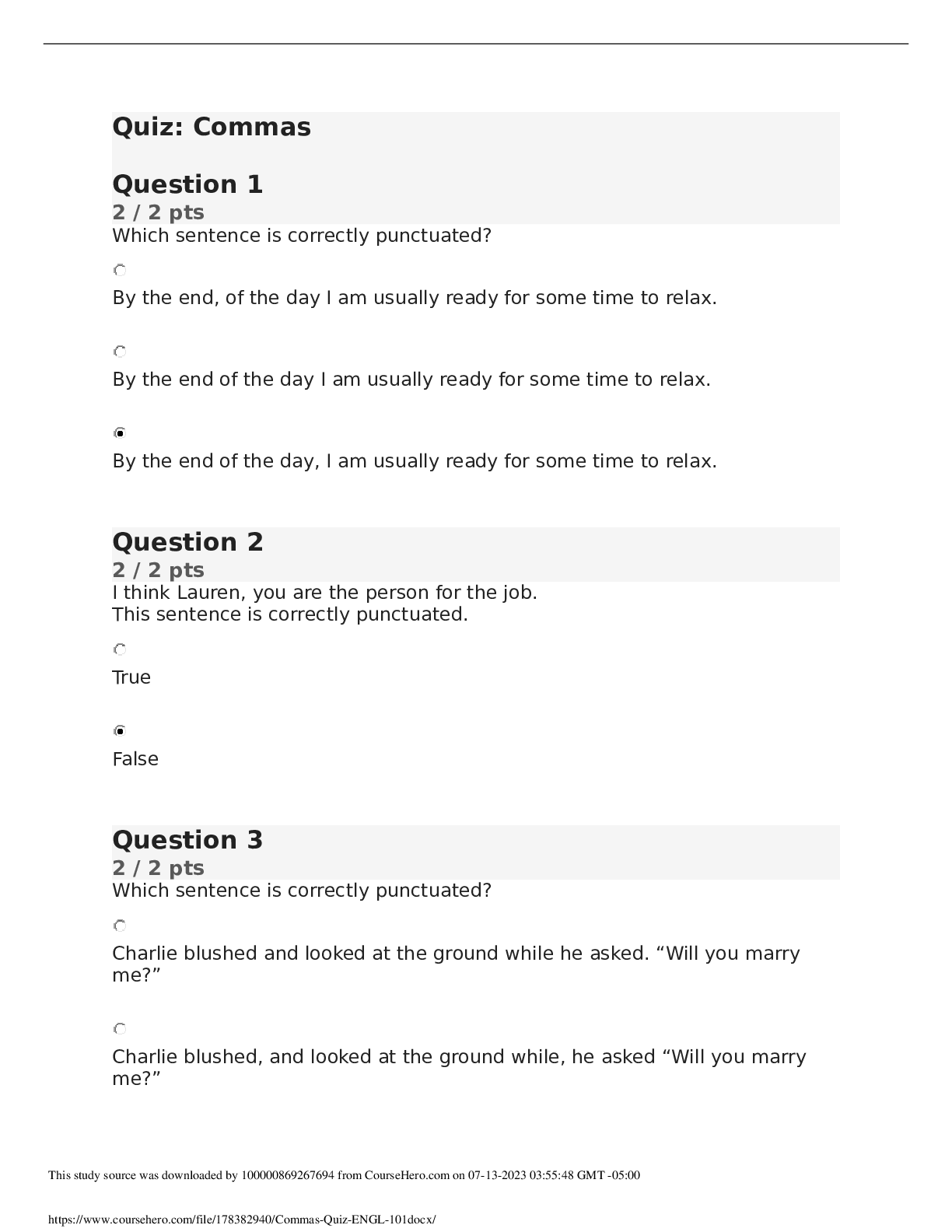
ENGL 101 Commas Quiz

$ 11

Unit 2-4 Study Guide - Will Merkle Unit 2 - Digital Information Lesson 1 INTRO TO MANAGEMENT 304

$ 3.5

A-level PHYSICS (7408/2) Paper 2 Mark scheme

$ 12

Pearson Edexcel IAL In AS/A Level Pure Mathematics P1 WMA11 Paper 01. Mark Scheme (Results) January 2022

$ 4

PEARSON EDEXCEL A LEVEL JUNE 2023 FURTHER MATHS QUESTION PAPER 1 - Core Pure Mathematics

$ 7

Essentials of Pathophysiology (1)

$ 30

MATH 225N Statistics Final EXAM – Chamberlain College of Nursing MATH 225N Statistics Final EXAM

$ 14.5

eBook Postharvest Physiology and Handling of Horticultural Crops 1st Edition By Ibrahim Kahramanoglu

$ 30

Franklin University - UNKNOWN 3WW(F13)3_Tayko_Software_problem_description.

$ 7

CHC - CCB Practice Test Questions with Verified Solutions

$ 10

2024 HESI Dental Hygiene Exam Guaranteed A+ Actual Questions and Answers, Complete 100%

$ 13

Facebook What is doing with data

$ 7

LAB: Warm up: Contacts ContactNode

$ 7

Math Assessment Part 1 Part 2 Liberty University answers complete solutions (ASSURED A)

$ 7.5

San Diego State UniversityPHYSICS 195Lab 1 physics -2-VERIFIED BY EXPERT TUTORS

$ 9

Introduction to Quantitative Research

$ 10

COMM 1 FINAL STUDY GUIDE: INTERCULTURAL COMMUNICATION ,100% CORRECT

$ 14

Wellcare ACT Mastery Exam Questions and Answers (Latest 2023 – 2024) Verified Solutions

$ 11

eBook [PDF] Proceedings of Data Analytics and Management ICDAM 2023 (Volume 3) 1st Edition By Abhishek Swaroop , Zdzislaw Polkowski , Sérgio D

$ 29

NUR211 Final Exam Study Guide

$ 14

AAPC CPC Chapter 11

$ 10

PHY-102-Motion Exercises-complete

$ 13

OCR Oxford Cambridge and RSA Thursday 9 June 2022 — Afternoon GCSE (9—1) in Combined Science B (Twenty First Century Science) J260/03 Physics (Foundation Tier) Time allowed: 1 hour 45 minutes

$ 8

Business > CASE STUDY > Cryptographic_Hash_Functions.docx (1) Cryptographic Hash Function DAT/305 Definition (All)

Cryptographic_Hash_Functions.docx (1) Cryptographic Hash Function DAT/305 Definition

Document Content and Description Below

Cryptographic_Hash_Functions.docx (1) Cryptographic Hash Function DAT/305 Definition A cryptographic hash function is a mathematical function used in cryptography and is an essential part of cybersecurity. Typical hash functions take inputs of variable lengths to return outputs of a fixed length. Cryptographic hash functions add security features to typical hash functions, making it more difficult to detect the contents of a message or information about recipients and senders.Â Hash functions are commonly used data structures in computing systems for tasks, such as checking the integrity of messages and authenticating information. While they are considered cryptographically "weak" because they can be solved in polynomial time, they are not easily decipherable. FrankenfieldÂ (2020). Cryptographic Hash Function Properties According toÂ BlockgeeksÂ (nd), cryptographic hash function is a special class of hash functions which has various properties making it ideal for cryptography. There are certain properties that a cryptographic hash function needs to have in order to be considered secure. Let™s run through them one by one. Property 1: Deterministic This means that no matter how many times you parse a particular input through a hash function you will always get the same result. This is critical because if you get different hashes every single time it will be impossible to keep track of the input. Property 2: Quick Computation The hash function should be capable of returning the hash of an input quickly. I. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. .. . . . . . . . . . . . . . . . . . .. . . . .

[Show More]

Last updated: 3 years ago

Preview 1 out of 5 pages

Buy Now

Instant download

We Accept: