SC/ MATH 1090 N WRITTEN ASSIGNMENT I SOLUTIONS | YORK UNIVERSITY

Document Content and Description Below

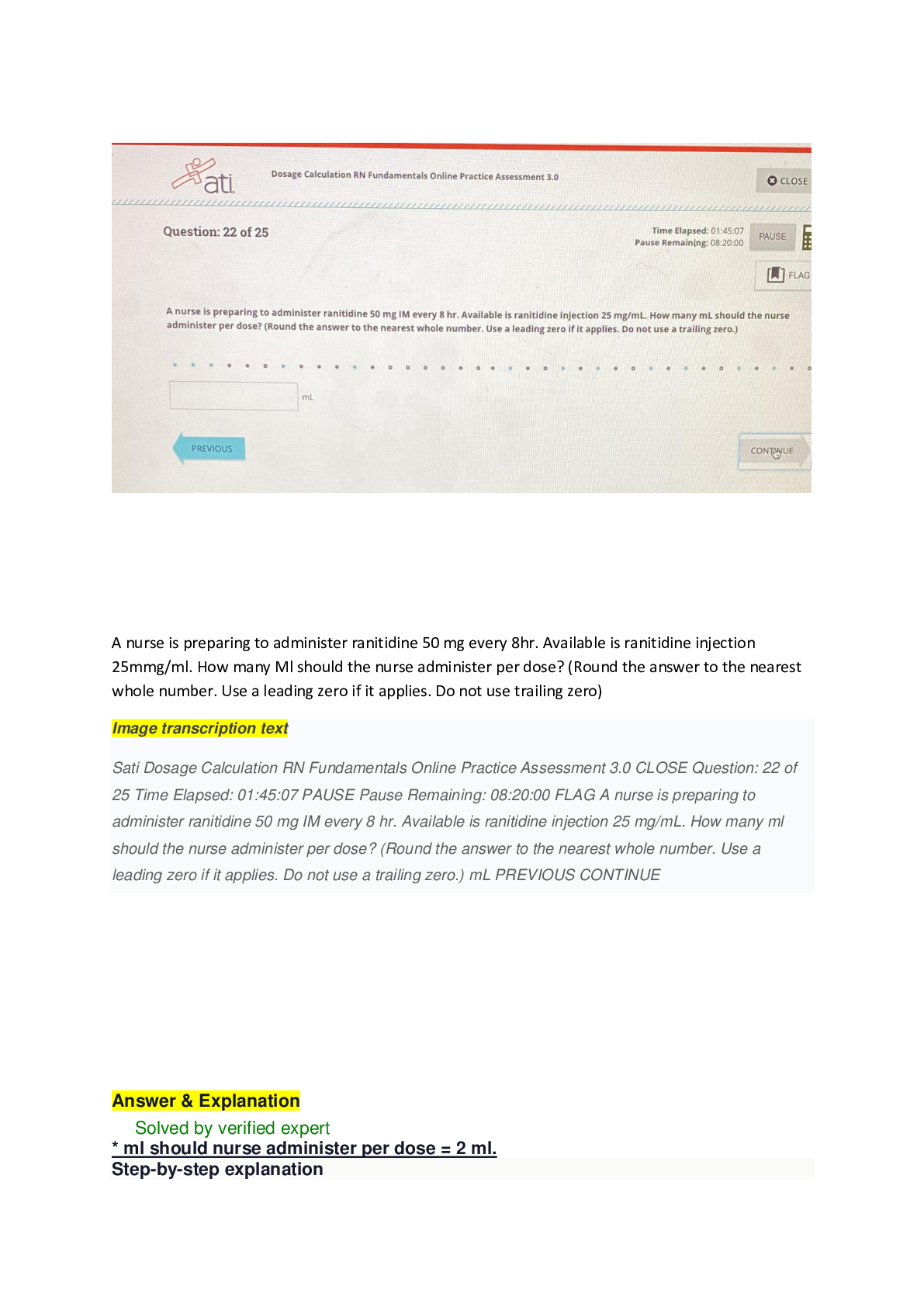
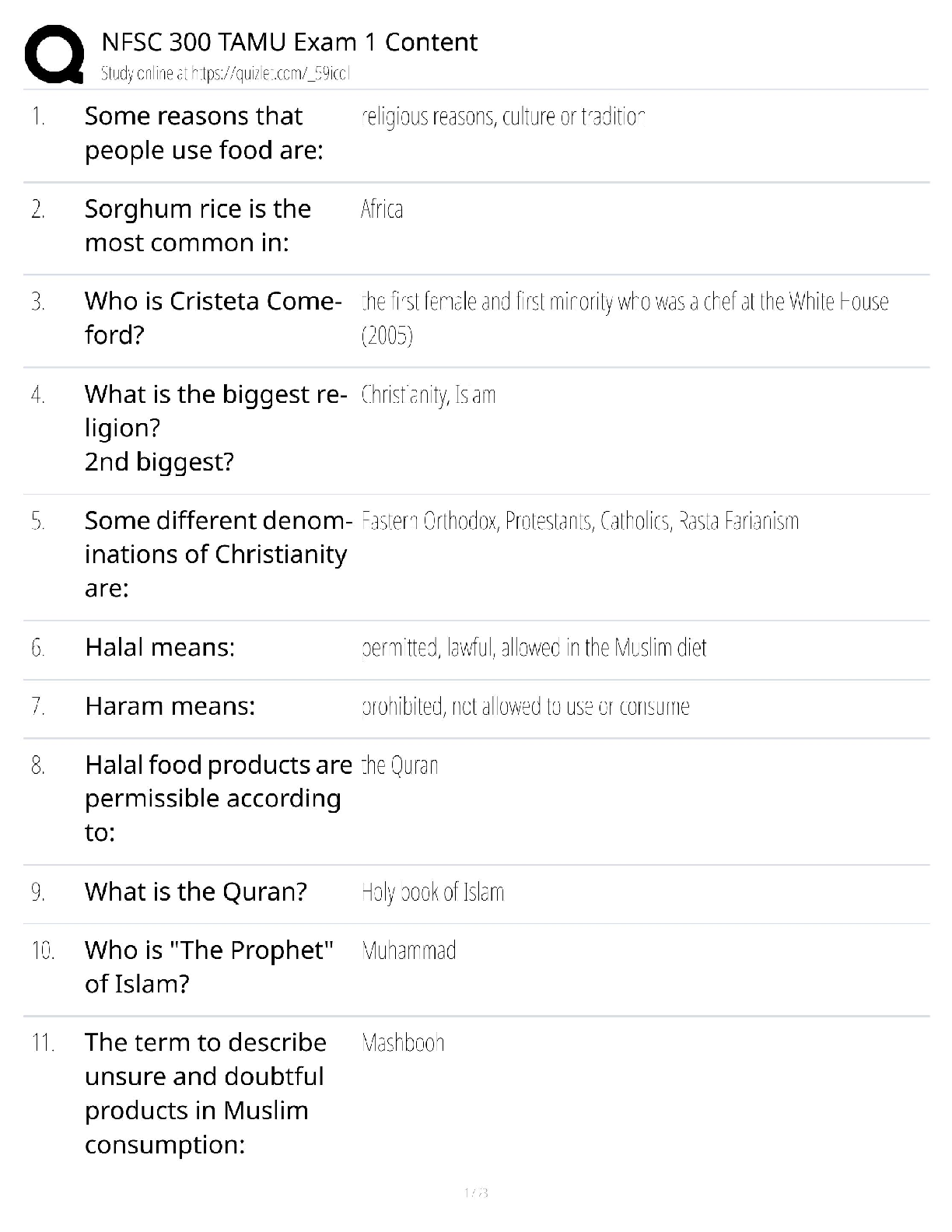
MATH MISC YORK UNIVERSITY SC/ MATH 1090 N WRITTEN ASSIGNMENT I SOLUTIONS The total number of points is 80. 1. (5+5 points) (a) Sketch the construction tree of the following propositional form ... ula ’ :((:r _ (r ^ :p)) $ (:::q ) r)): Give its complexity c(’) and list all of its subformulas (without repetition). How many distinct subformulas are there? Solution.   :::q; r; ::q; :q; :p, p; q, so 13 distinct subformulas in total (atomic formula r has 3 occurrences in ’). (b) Use structural induction on the complexity of formula ’ to show that the number of occurrences of the symbol ^ in ’ is less than or equal to the number of left brackets in ’. Date: Jan 13. Due date Jan 28, end of day. 1 2 YORK UNIVERSITY SC/ MATH 1090 N WRITTEN ASSIGNMENT I SOLUTIONS Solution. Let N(’) be the number of occurrences of the symbol ^ in ’ and let LB(’) be the number of left brackets in ’. Basis Step. n = c(’) = 0: If c(’) = 0 for some formula ’ 2 S(P), then ’ has no connectives involved, i.e. ’ is atomic, so N(’) = 0 and LB(’) = 0 whence 0 ≤ 0 is true. Thus N(’) ≤ LB(’) holds. Inductive Step. Suppose (this is our Inductive Hypothesis (IH)) that for all formulas ’ 2 S(P) with s(’) ≤ n, where n ≥ 0, the required inequality N(’) ≤ LB(’) holds. Consider a formula ’ 2 S(P) with c(’) = n+1. Since n ≥ 0, we have n+1 ≥ 1, so ’ contains at least one connective and hence contains the principal connective that may be one of :; ^; _; ); $. Therefore ’ must be one of the following formulas: :θ, (θ ^ ); (θ _ ); (θ ) ); (θ $ ); where θ; 2 S(P) with c(θ) ≤ n and c( ) ≤ n. For :θ we clearly have N(:θ) = N(θ) and LB(:θ) = LB(θ). Since c(θ) ≤ n, by IH N(θ) ≤ LB(θ) = LB(:θ) whence N(:θ)) ≤ LB(:θ). For (θ ^ ) we clearly have N((θ ^ )) = N(θ) + N( ) + 1 and LB((θ ^ )) = LB(θ) + LB( ) + 1. Since c(θ) ≤ n and c( ) ≤ n, by the IH N(θ) ≤ LB(θ) and L( ) ≤ NB( ) whence N((θ ^ )) = N(θ) + N( ) + 1 ≤ LB(θ) + LB( ) + 1 = LB((θ ^ )); so indeed, N((θ ^ )) ≤ LB((θ ^ )): Similar arguments work in 3 remaining cases where we do not add 1 to the sum while computing N((θ _ )); N((θ ) )); and N((θ $ )); but 1 left bracket is added, so 1 must be added to the sum while computing LB(((θ_ )); LB((θ ) )); and LB((θ $ )) yielding strict inequalities. N((θ _ )) = N(θ) + N( ) ≤ LB(θ) + LB( ) < LB(θ) + LB( ) + 1 = LB((θ _ )) and similarly for (θ ) ) and (θ $ ). Thus the required inequalities hold as well, so in all cases N(’) ≤ LB(’) and this completes the inductive step. 2. (5+5 points) (a) Prove that for all ’; 2 S(P), ’ ≡ (i.e. ’ and are logically equivalent) iff (’ $ ) is a tautology: Solution. ’only if’ part ()). Let ’ ≡ . Take any truth assignment v : S(P) ! B. We then have v(’) = v( ), that is, these values are either both T or both F, so v(’ $ ) = F$(v(’); v( )) = T by the definition of the truth function F$, so ’ $ is a tautology. ’if’ part (() Let ’ $ be a tautology. Then for any truth assignment v : S(P) ! B, v(’ $ ) = T: But because v(’ $ ) = F$(v(’); v( )); we have F$(v(’); v( )) = T, so v(’) and v( ) must be either both T or both F by the definition of F$, i.e. v(’) = v( ), for any v : S(P) ! B, hence ’ ≡ . (b) Show that if ’ and (’ ) ) are tautologies, then so is . Solution. Let both ’ and (’ ) ) be tautologies, that is, for every truth assignment v : S(P) ! B, we have v(’) = v((’ ) )) =T. Then, since v((’ ) )) = F)(v(’); v( )), we have F)(v(’); v( )) =T, where v(’) =T, so [Show More]

Last updated: 5 months ago

Preview 1 out of 5 pages