CS 70 Final Review Spring 2017. Questions and Answers. Includes Worked Solutions.

Document Content and Description Below

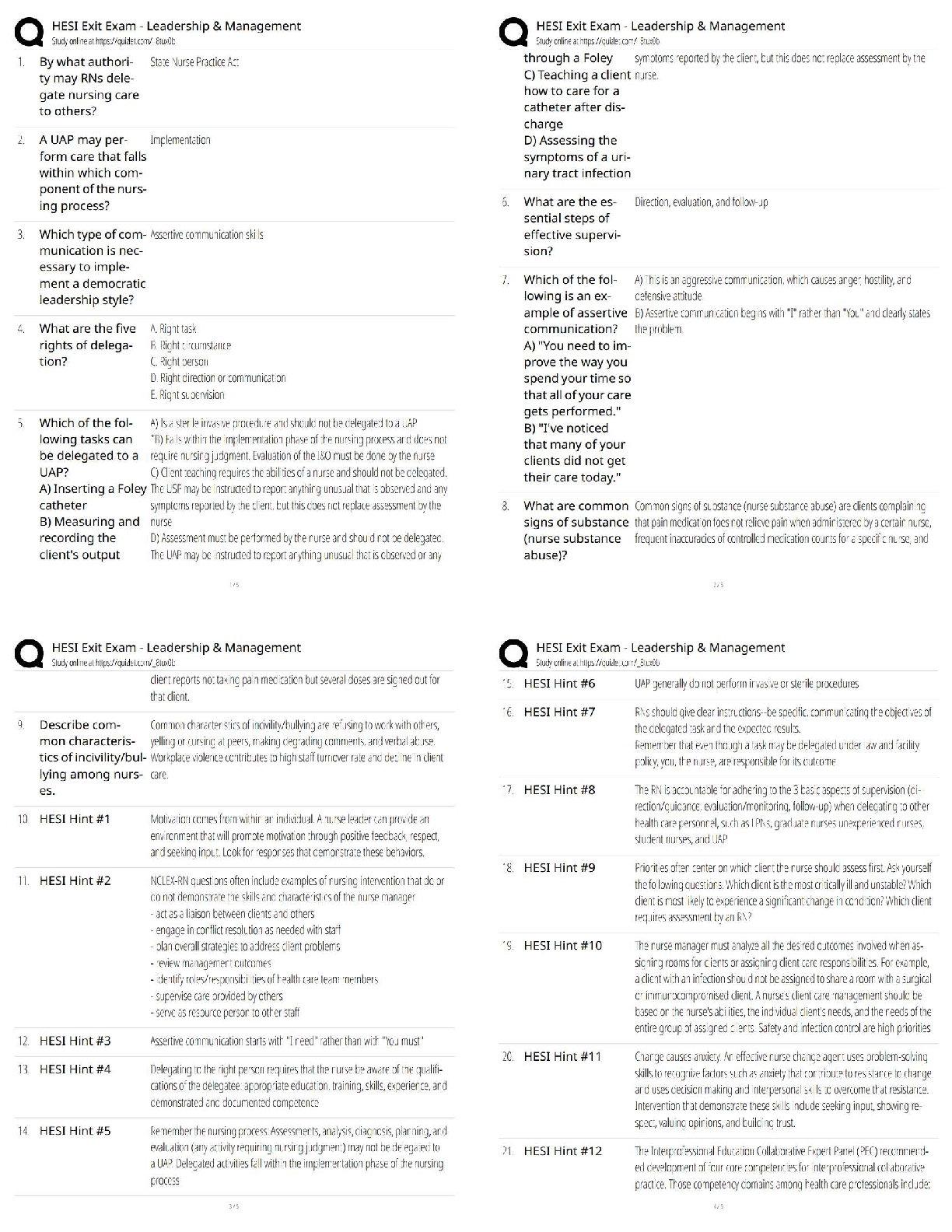
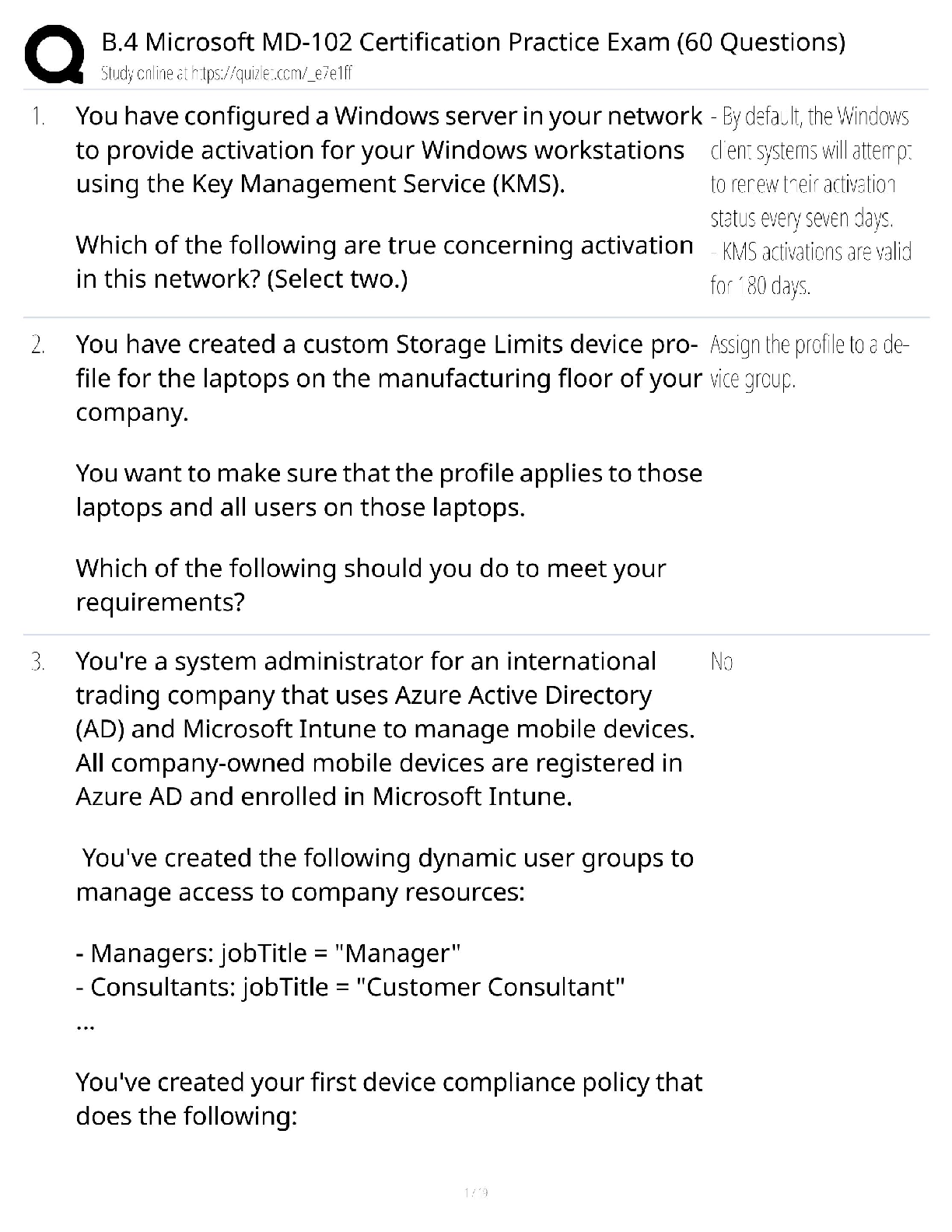
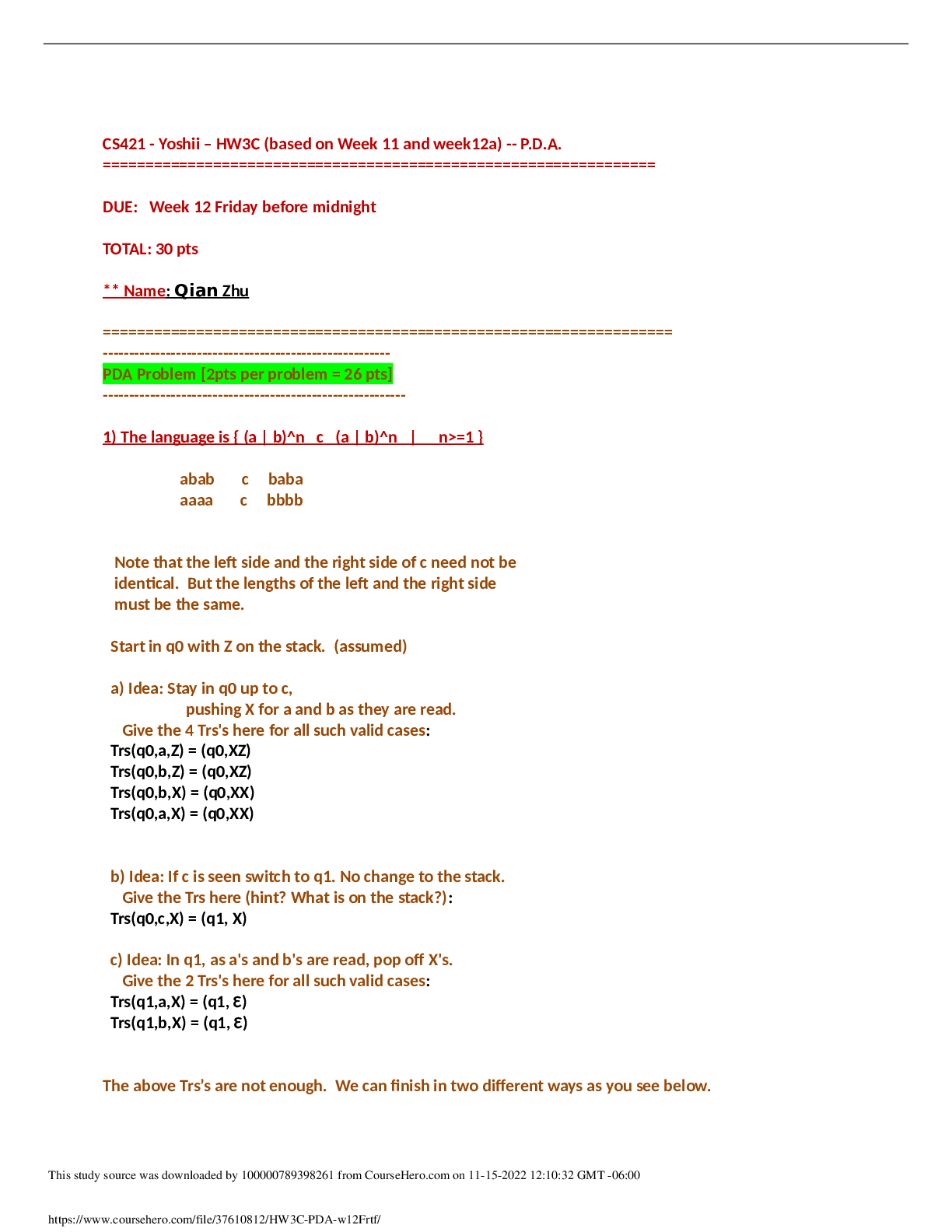
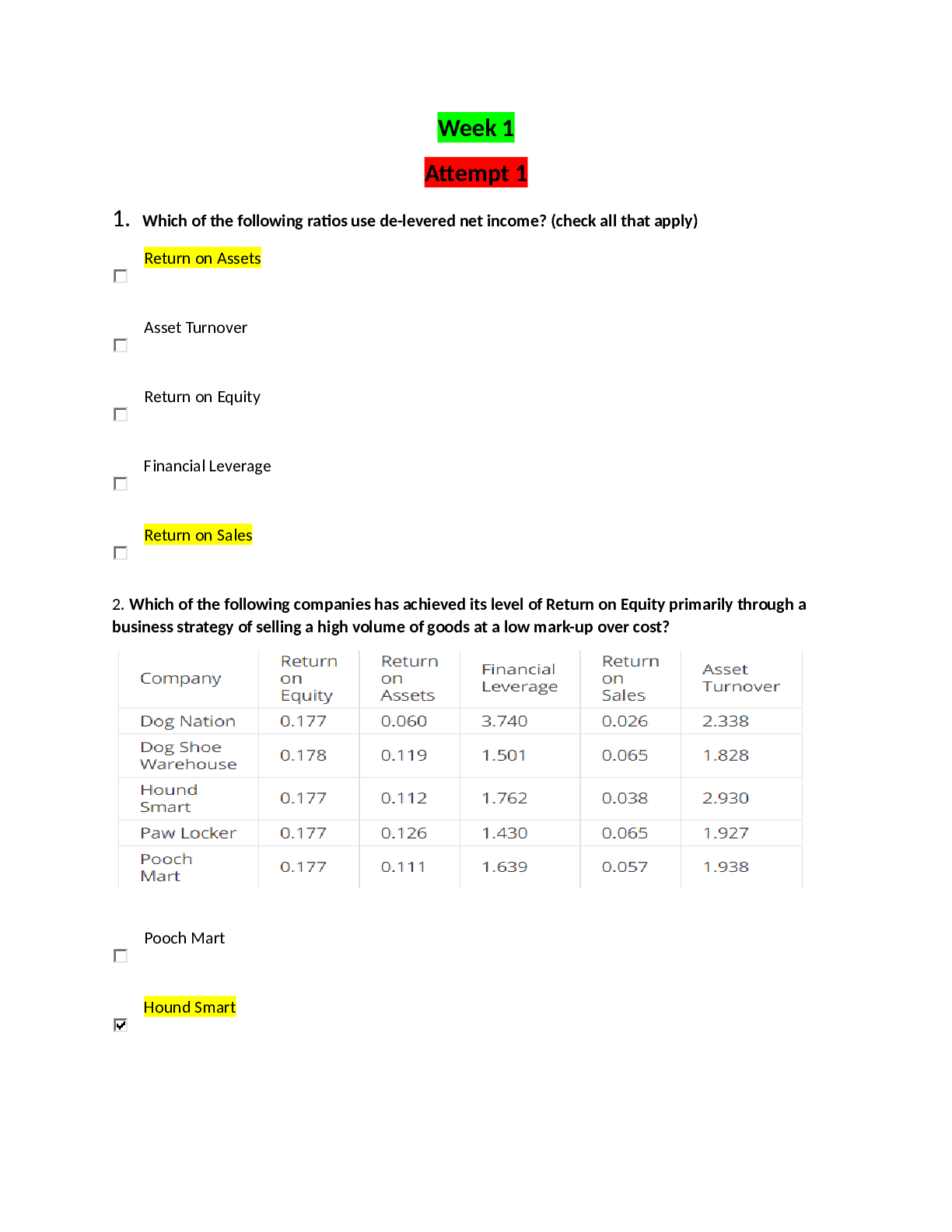
CS 70 Final Review Spring 2017 May 4, 2017 I Similar format to Midterms. Final Details I Similar format to Midterms. I Lots of questions. Final Details I Similar format to Midterms. I Lots ... of questions. I Comprehensive. Expect slightly more on omitted parts from MT2 (Polynomials/counting) and post-MT2 material. Agenda I 7 Questions: You try problems, we present solutions. I 7 Questions: You try problems, we present solutions. I Don’t write up a complete solution to each question in the allotted time - but do think about an approach. I 7 Questions: You try problems, we present solutions. I Don’t write up a complete solution to each question in the allotted time - but do think about an approach. I Questions: After we present solutions, and on Piazza. I (a) X is a random variable such that X > -5 and E[X ] = -3. Find an upper bound for the probability of X being greater than or equal to -1. I (b) You roll a die 100 times. Let Y be the sum of the numbers that appear on the die throughout the 100 rolls. Use Chebyshevs inequality to bound the probability of the sum Y being greater than 400 or less than 300. (a) X is a random variable such that X > -5 and E[X ] = -3. Find an upper bound for the probability of X being greater than or equal to -1. Recall that Markov’s Inequality only applies to non-negative random variables. (b) You roll a die 100 times. Let Y be the sum of the numbers that appear on the die throughout the 100 rolls. Use Chebyshevs inequality to bound the probability of the sum Y being greater than 400 or less than 300. Define Xi as the number on the die on the i-th roll, Y = P100 i=1 Xi. Coins of LLSE There are 3 coins in a bag, biased at 1=3, 1=2, 2=3 (bias means the chance the coin will be heads). After picking a coin randomly, you flip the coin 4 times. Let Xi be the indicator variable that the ith flip is heads. Let X = P1≤i≤2 Xi and Y = P3≤i≤4 Xi. Find Gambling Woes Forest proposes a gambling game to you (uh oh!). Every day, you flip two independent fair coins. If both of the coins come up heads, then your fortune triples on that day. If one coin comes up heads and the other coin comes up tails, then your fortune is cut in half. If both of the coins comes up tails, then game over: you lose all of your money! Forest claims that you can get rich quickly with this Recall: E[A j B] is the conditional expectation of A given B. A function of B! E[Mn+1 j Mn] is a function of Mn. Recall: E[A j B] is the conditional expectation of A given B. A function of B! E[Mn+1 j Mn] is a function of Mn. replace m with Mn to get the best estimate as a function of Mn. Recall: E[A j B] is the conditional expectation of A given B. A function of B! E[Mn+1 j Mn] is a function of Mn. Approach: Assume Mn = m. Treat m like a constant to find the best estimate E[Mn=1 j Mn = m]. Then replace m with Mn to get the best estimate as a function of Mn. Definition of conditional expectation: where k are the possible values of Mn=1 given that Mn = m. What are the values of k? Solution Forest proposes a gambling game to you (uh oh!). Every day, you flip two independent fair coins. If both of the coins come up heads, then your fortune triples on that day. If one coin comes up heads and the other coin comes up tails, then your fortune is cut in half. If both of the coins comes up tails, then game over: you lose all of your money! Forest claims that you can get rich quickly with this scheme, but you decide to calculate some probabilities first. (b) Use the law of iterated expectation to calculate E[Mn+1] in terms of E[Mn]. Solve your recurrence to obtain an expression for E[Mn+1] in terms of M0. Do you think this is a fair game? Iterated Expectation / Total Expectation: Iterated Expectation / Total Expectation: Iterated Expectation / Total Expectation: Your expected fortune never changes! Technically, we would be justified in calling this a fair game. Gambling Woes Forest proposes a gambling game to you (uh oh!). Every day, you flip two independent fair coins. If both of the coins come up heads, then your fortune triples on that day. If one coin comes up heads and the other coin comes up tails, then your fortune is cut in half. If both of the coins comes up tails, then game over: you lose all of your money! Forest claims that you can get rich quickly with this scheme, but you decide to calculate some probabilities first. (c) Calculate Pr(Mn > 0). What is the behavior as n ! 1? Would you still play this game? How would the event Mn > 0 occur? How would the event Mn > 0 occur? If and only if you never go bust. Every day, you have a probability of 3 4 of not going bust. This must happen for n days, so How would the event Mn > 0 occur? If and only if you never go bust. Every day, you have a probability of 3 4 of not going bust. This must happen for n days, so Pr[Mn > 0] = 34 n As n ! 1, (3=4)n ! 0, so after many days of playing the game, it is highly probable that we are broke! How would the event Mn > 0 occur? If and only if you never go bust. Every day, you have a probability of 3 4 of not going bust. This must happen for n days, so Pr[Mn > 0] = 34 n As n ! 1, (3=4)n ! 0, so after many days of playing the game, it is highly probable that we are broke! Conclusion: Don’t just consider expectation when evaluating a random variable; the distribution is extremely important. In this case, Mn ! 0 but E[Mn] 6! 0. Markov Maze { Solution Overall View of a Markov Chain Problem: I What is the problem asking I How to define a optimal set of states with easy-to-express transition matrix I Identify the initial distribution the above information defines a Markov Chain and is all we need to know for solving any Markov Chain problem. Markov Maze { Solution states: 1 ≡ corner squares 2 ≡ edge squares 3 ≡ center squares Corners(1) Edges(2) Center(3) Markov Maze { Solution states: 1 ≡ corner squares 2 ≡ edge squares 3 ≡ center squares Corners(1) Edges(2) Center(3) 13 123 quick check: I All edges coming out of a state should have transitions sum up to 1. (a)Write down the transition matrix and the balance equations for this problem. Corners(1) transition matrix Markov Maze { Solution (a) balance equation π = πP where P is the transition matrix. ) (b)Is this Markov chain irreducible? Markov Maze { Solution (b) Corners(1) Edges(2) Center(3) 1 13 123 Yes. Pick any two states, you can find a path to reach one from the other. (c)Is this Markov chain periodic? If so, what is its period? (e)Do the values of Pr[Xn = i] necessarily converge as n increases? If so, what values do they converge to? If not, give a counterexample where the values of Pr[Xn = i] oscillate. Alvin is playing darts. His aim follows an exponential distribution; that is, the probability density that the dart is x distance from the center is fX (x) = e-x. The board’s radius is 4 units. I What is the probability the dart will stay within the board? I Say you know Alvin will always make it within the board. What is the probability he is within 1 unit from the center? I If Alvin is within 1 unit from the center, he scores 4 points, if he is within 2 units, he scores 3, etc. If the dart ends up outside the board, he scores 0. In other words, Alvin scores b5 - xc for x ≤ 4, where x is the distance from the center. What is Alvin’s expected score after one throw? I Say you know Alvin will always make it within the board. What is the probability he is within 1 unit from the center? Exponential Median What is the expected value of the median of three i.i.d exponential variables with parameter λ? Recall that if X1 < X2 < X3, X2 is the median. Exponential Median Recall the following useful facts of exponential random variables I It’s memoryless, i.e. if X ∼ Exp(λ), For arbitrary random variables, in general, we also have the following properties: I X1; X2 independent I d Exponential Median More hints: If you decide to solve the problem using CDF, it helps to think, if median of the three variable M is ≤ m, what does this imply about the values for the other two? (4) Solution We first present the solution using CDF [Show More]

Last updated: 2 years ago

Preview 1 out of 68 pages