Financial Accounting > QUESTIONS & ANSWERS > ACC 557 Week 3 Homework | Strayer University, Washington (All)

ACC 557 Week 3 Homework | Strayer University, Washington

Document Content and Description Below

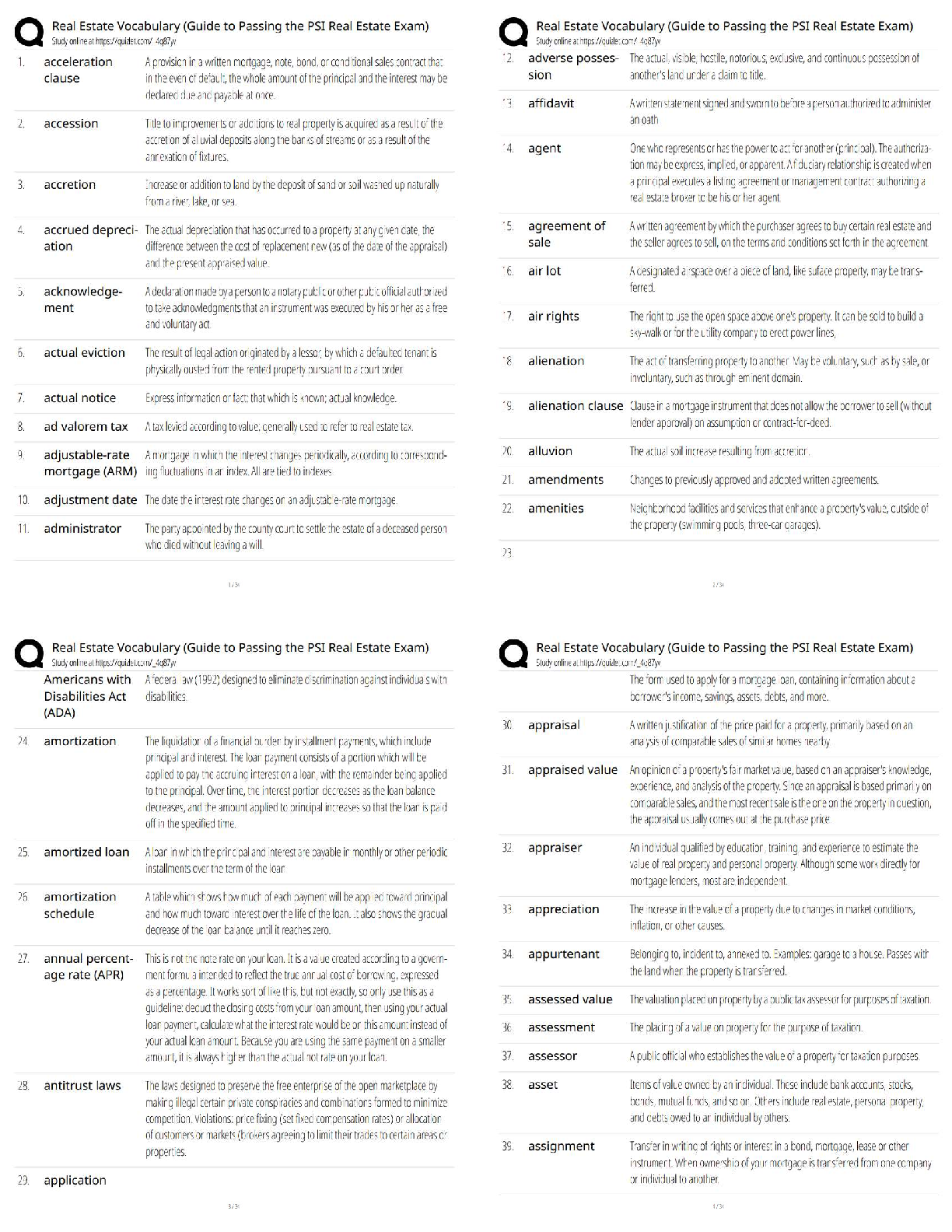
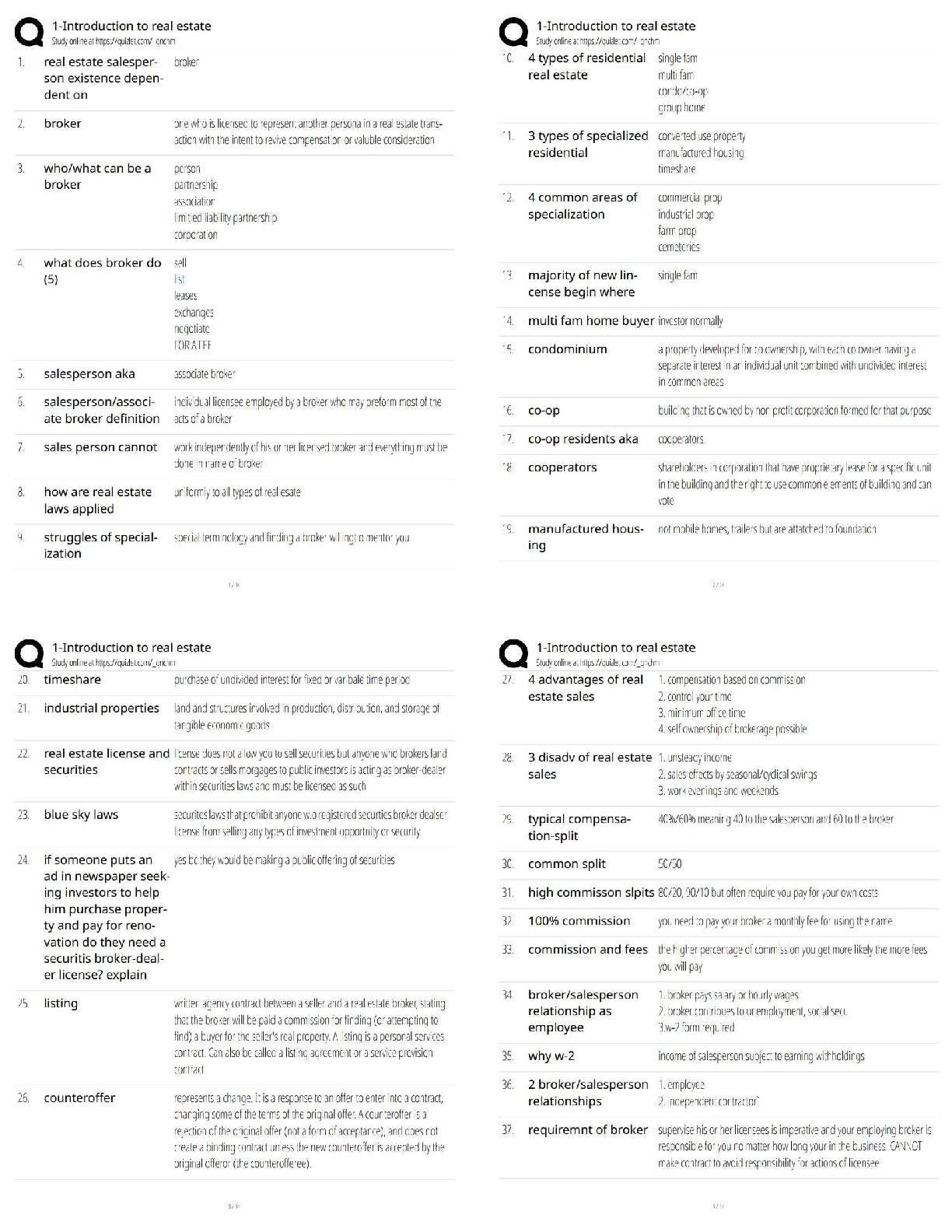
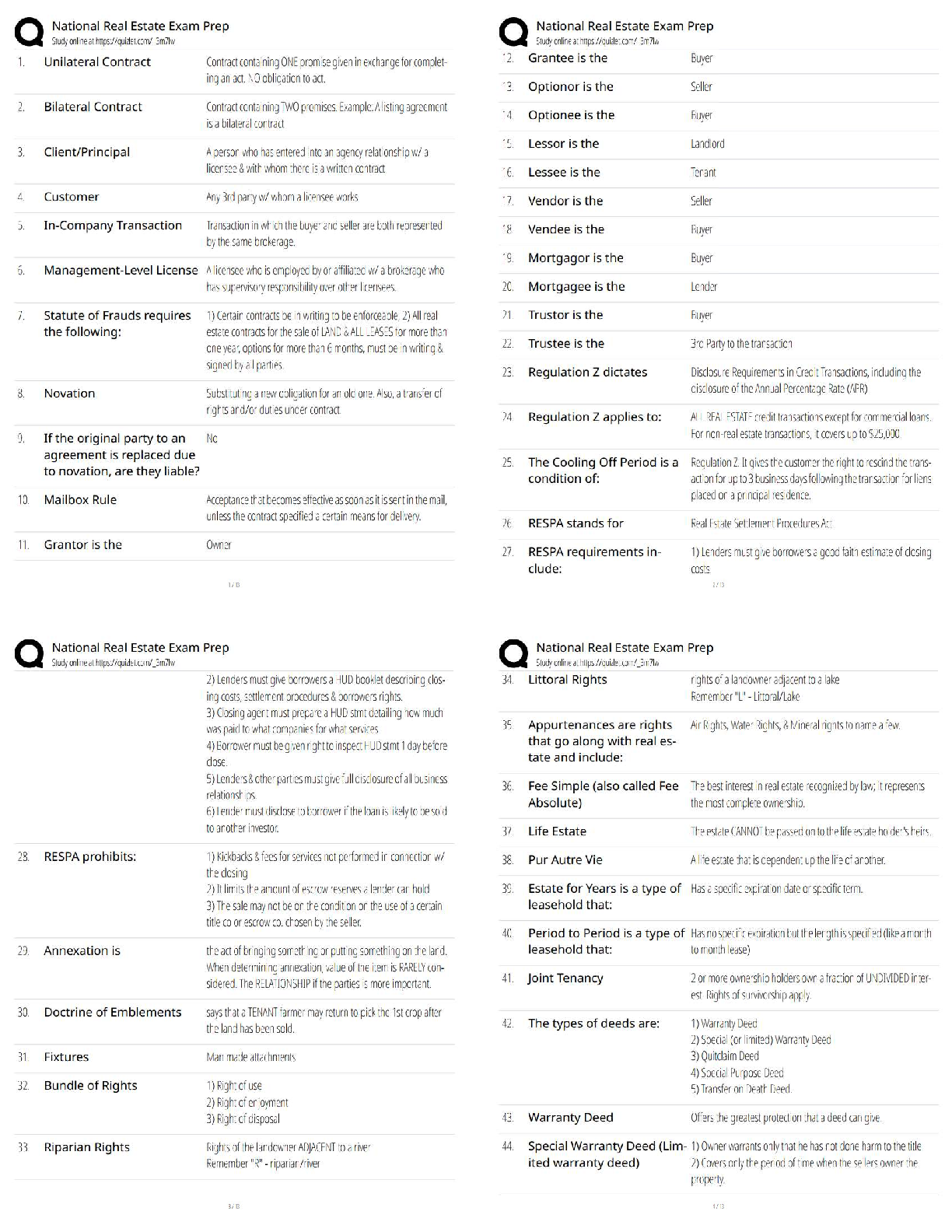
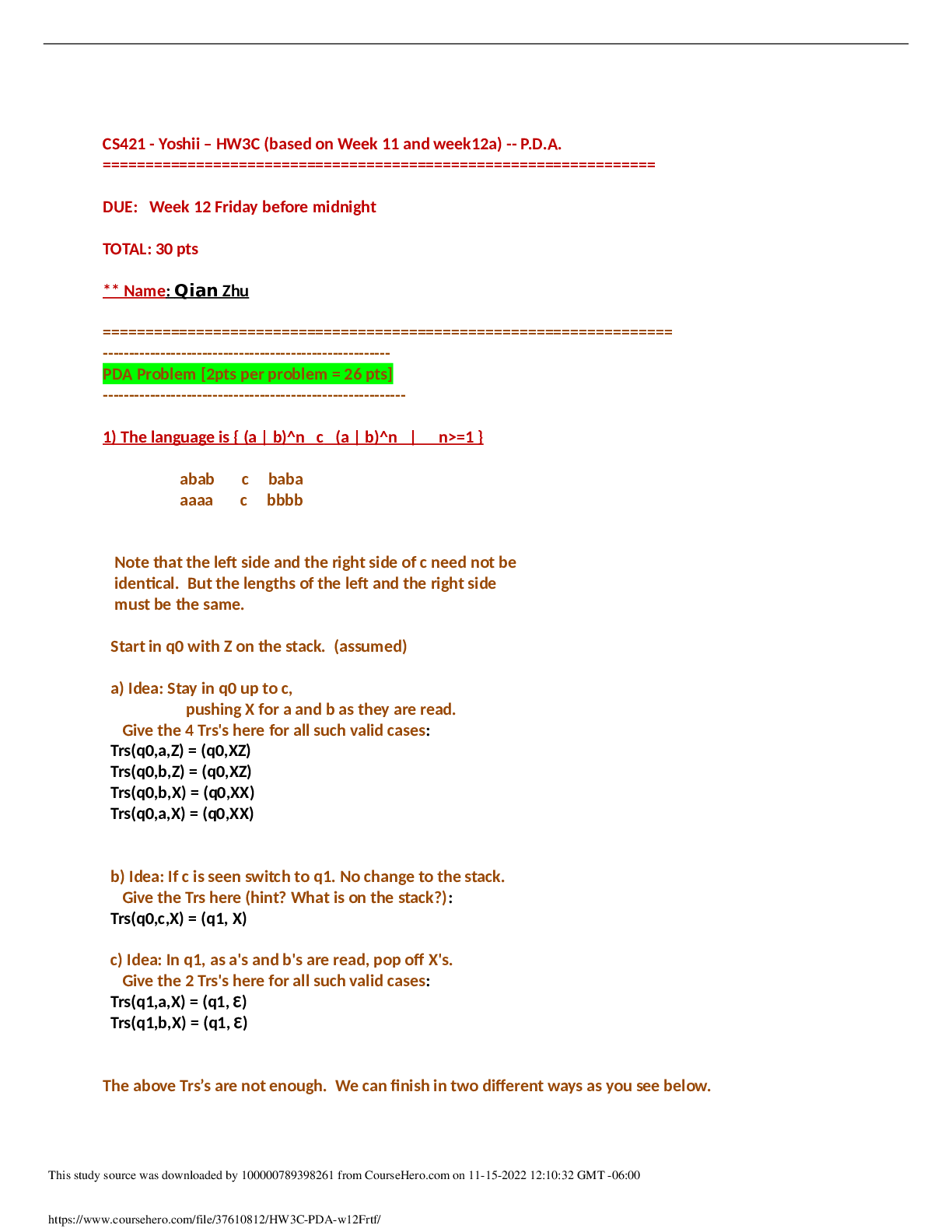
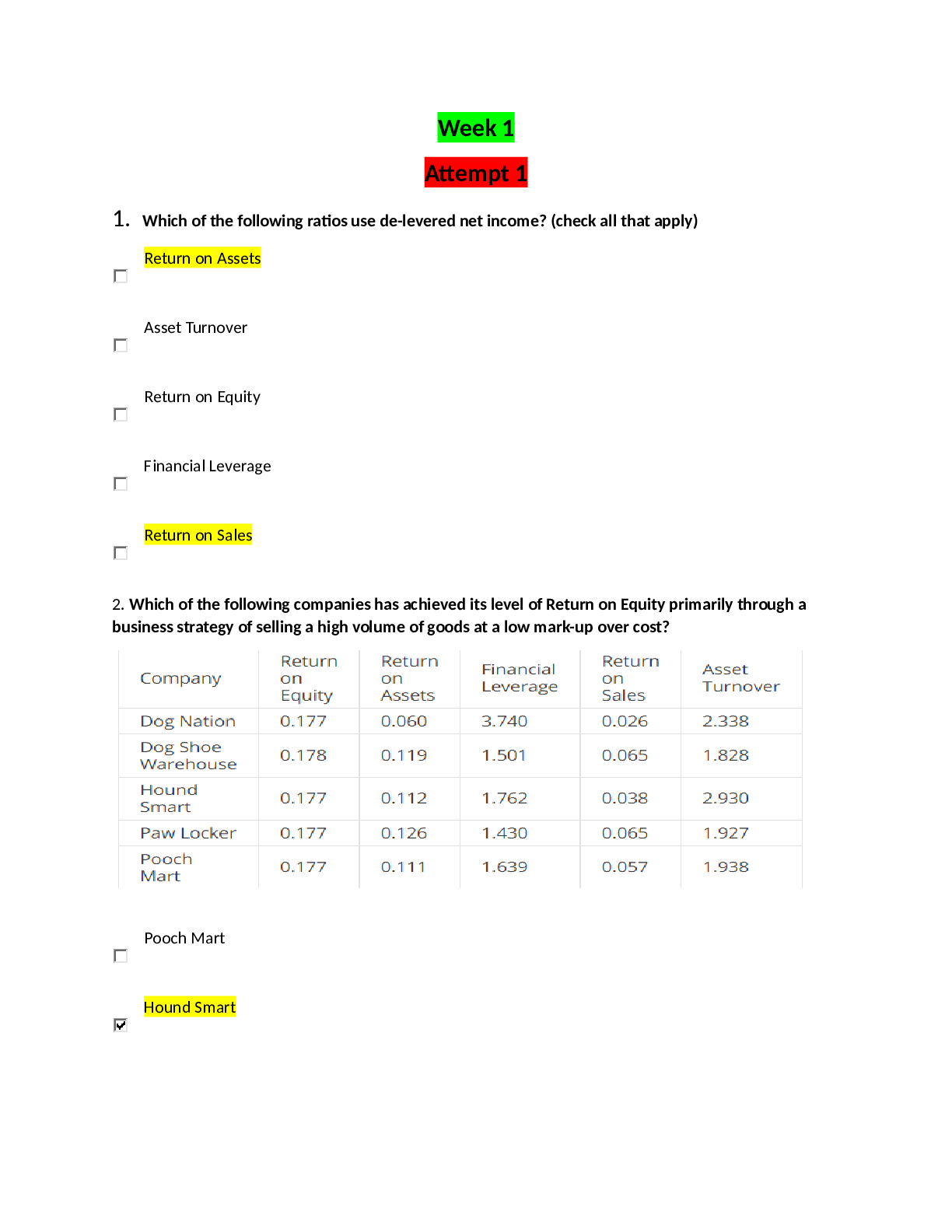
ACC 557 Week 3 Homework | Strayer University, WashingtonWeek 3 1. Using the estimation technique described in Step 3.1, what percentage of your investment would you allocate to WFC and MSFT, respectively, to arrive at a portfolio with the minimum variance? 40%, 60% 45%, 55% 60%, 40% 55%, 45% 2. Using the Solver technique described in Step 3.2, what more precise percentage of your investment would you allocate to WFC and MSFT, respectively, to arrive at a portfolio with the minimum variance? 44.3%, 55.7% 55.3%, 44.7% 44.7%, 55.3% 59.2%, 40.8% 3. Using the same Solver techniques, what would be the weight for WFC in the "optimal risky portfolio" on the efficient frontier consisting of WFC and MSFT? Write your answer as a percentage, with no percentage symbol ("%"), rounded to the nearest tenth percentage point (e.g., you would write "48.1234%" as "48.1", not "0.481234"). Hint: Your goal now is to find the maximum value of the Sharpe Ratio of the portfolio. Assume the "risk free asset" rate = 0. 0.99 4. Compare your optimal risky portfolio characteristics to those of the two individual stocks used in the portfolio. What do you find? - The optimal risky portfolio displays a higher Sharpe Ratio than either of the two stocks used in the portfolio. - The optimal risky portfolio displays a lower Sharpe Ratio than either of the two stocks used in the portfolio. - The optimal risky portfolio displays the same Sharpe Ratio as at least one of the two stocks used in the portfolio. 5. Refer to Step 3.3. In the "Unconstrained" or "Short Selling" version of the optimal risky portfolio, what is the weight for XOM? Write your answer as a percentage, with no percentage symbol ("%"), rounded to the nearest tenth percentage point (e.g., you would write "48.1234%" as "48.1", not "0.481234"). Hint: You can use the same logic and Solver built from Step 3.2. 6. Refer to Step 3.3. In the "Constrained" or "Long Only" version of the optimal risky portfolio, what is the weight for GOOG? Write your answer as a percentage, with no percentage symbol ("%"), rounded to the nearest tenth percentage point (e.g., you would write "48.1234%" as "48.1", not "0.481234"). Hint: You can use the same logic and Solver built from Step 3.2. 7. Refer to Step 3.3. In the "Unconstrained" or "Short Selling" version of the optimal risky portfolio, what is the portfolio mean? Write your answer as a percentage, with no percentage symbol ("%"), rounded to the nearest hundredth percentage point (e.g., you would write "48.1234%" as "48.12", not "0.481234"). 8. Refer to Step 3.3. In the "Constrained" or "Long Only" version of the optimal risky portfolio, what is the portfolio standard deviation? Write your answer as a percentage, with no percentage symbol ("%"), rounded to the nearest hundredth percentage point (e.g., you would write "48.1234%" as "48.12", not "0.481234"). 9. Refer to Step 3.3. In the "Unconstrained" or "Short Selling" version of the optimal risky portfolio, what is the portfolio Sharpe Ratio? Write your answer as a number rounded to the nearest thousandth percentage point (e.g., you would write "0.073214" as "0.073"). 10. Comparing the two optimal risky portfolios (one allowing short selling and the other long-only), what do you find regarding the Sharpe Ratios? - When short selling is allowed, the portfolio is able to attain a higher level of Sharpe Ratio - When only long selling is allowed, the portfolio is able to attain a higher level of Sharpe Ratio - The Sharpe Ratio is the same

[Show More]

Last updated: 1 year ago

Preview 1 out of 2 pages

Buy Now

Instant download