This document contains my own solutions to the problems proposed at the
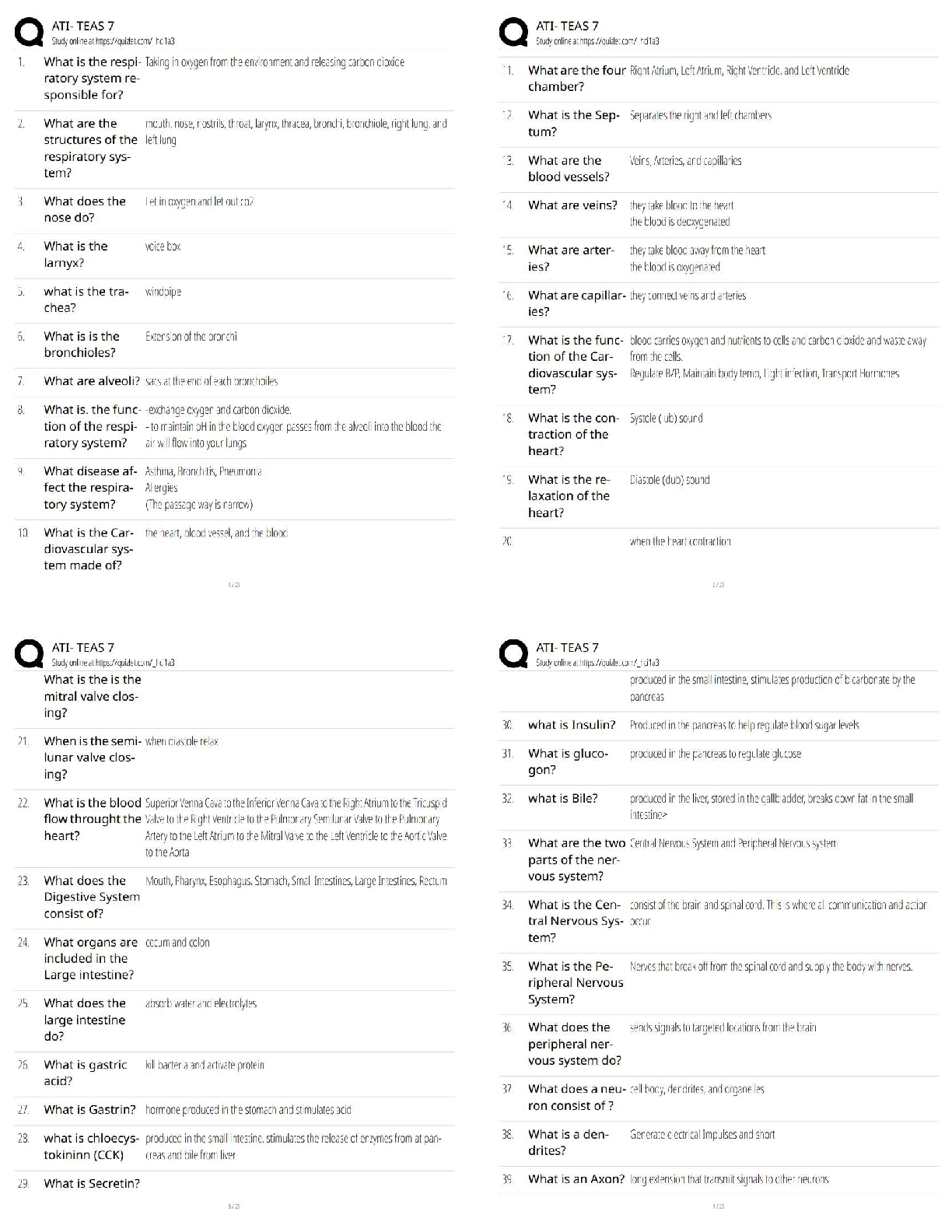
end of each chapter of the book "Process Modelling, Simulation and Control
for Chemical Engineers" Second Edition, by William L. Luyben. As such,
...
This document contains my own solutions to the problems proposed at the
end of each chapter of the book "Process Modelling, Simulation and Control
for Chemical Engineers" Second Edition, by William L. Luyben. As such, I
can’t guarantee that the proposed solutions are free from errors. Think about
them as a starting point for developing or as a means of checking your own
solutions. Any comments or corrections will be appreciated. Contact me at
[email protected]
The computer programs developed for this chapter (Matlab) are available
at:
https://www.dropbox.com/
sh/zknqiqgfynqafxj/AAB07C-RHQ J7hkUTZkDnvaTa?dl=0
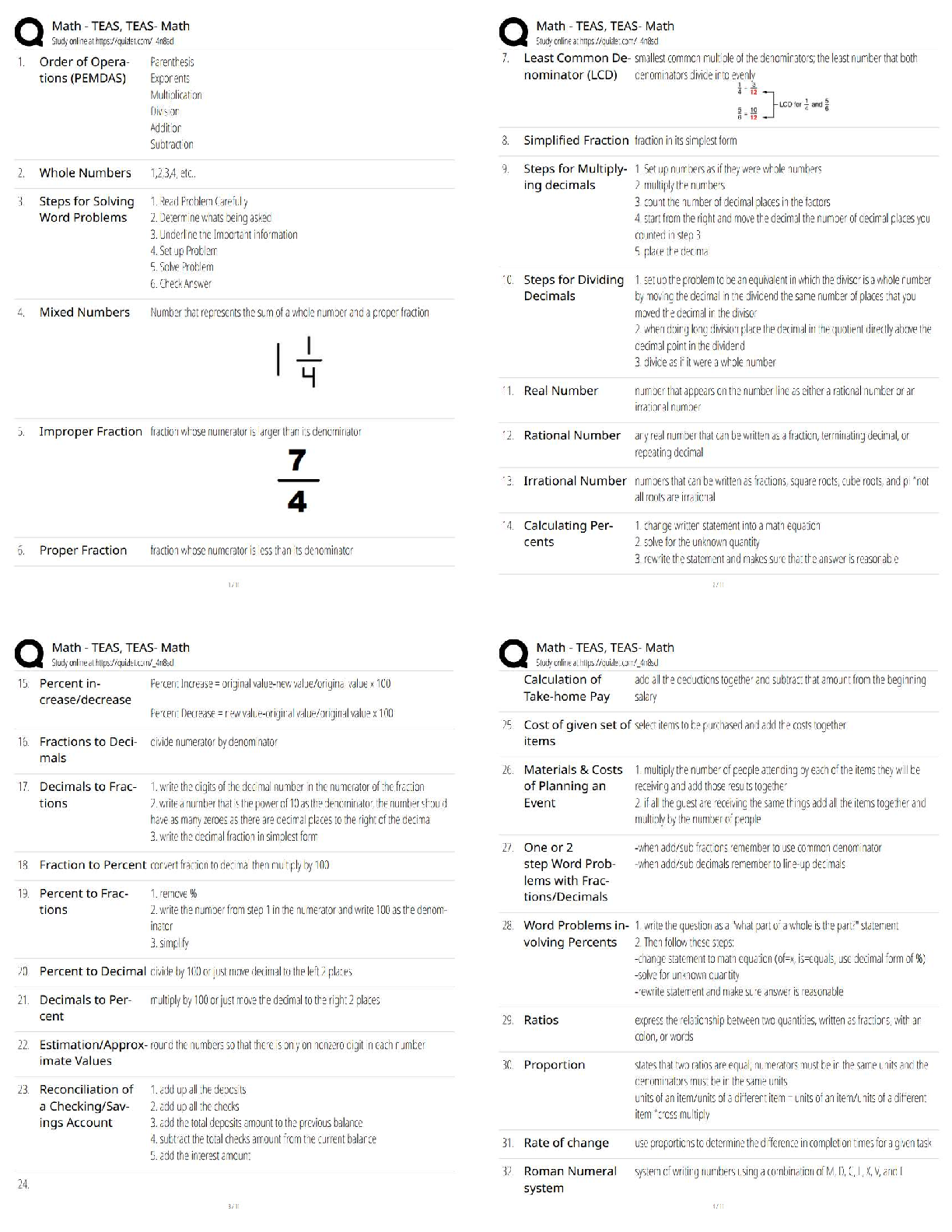
Problem 14
Solve the ODE derived in Problem 3.4 to show that the concentration C in
Grandpa McCoy’s batch of Liquid Lightning is:
C(t) = C0(1 −kte−kt)
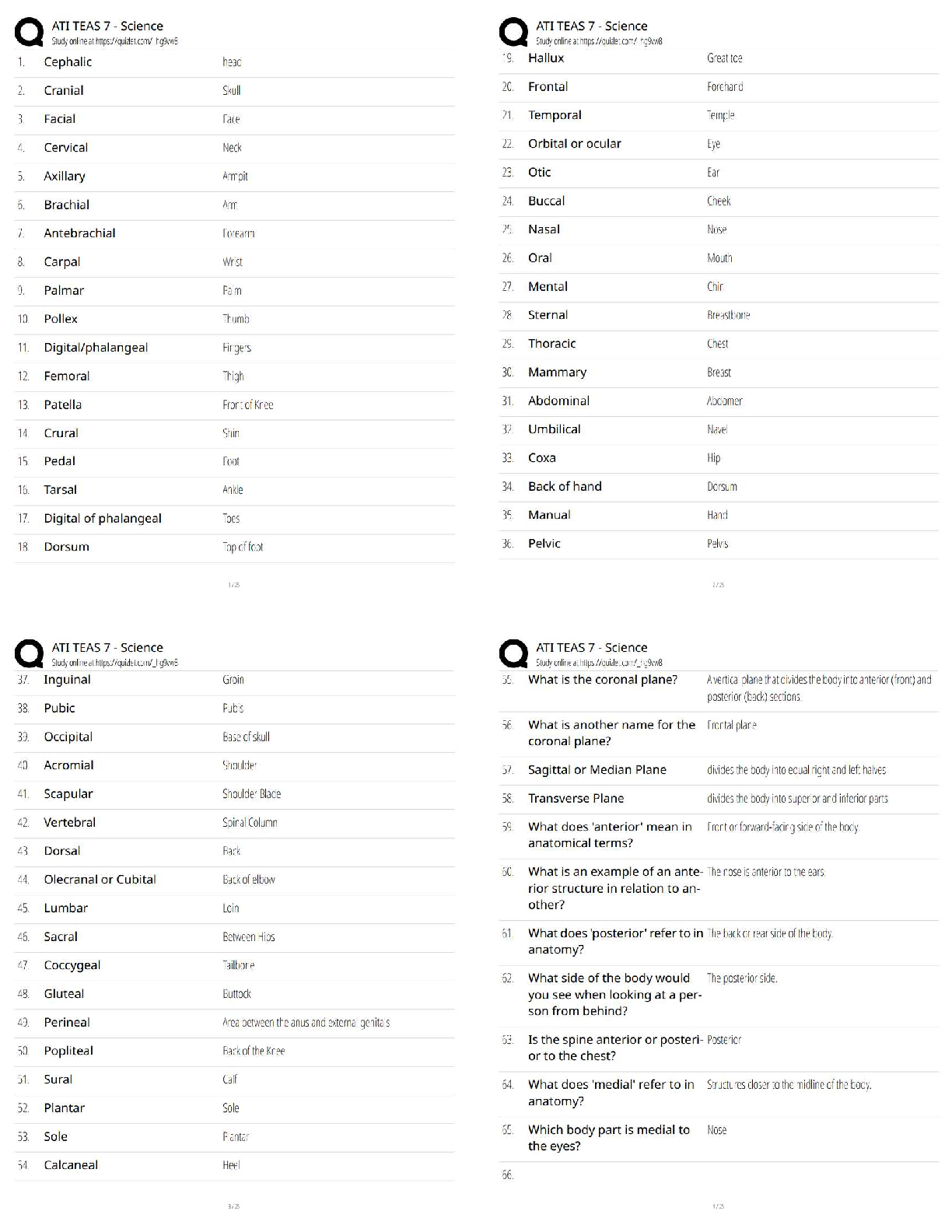
Problem 15
Suicide Sam slipped his 2000 lbm hot rod into neutral as he came over the crest
of a mountain at 55 mph. In front of him the constant downgrade dropped 2000
feet in 5 miles, and the local acceleration of gravity was 31.0 ft=s2.
Sam maintained a constant 55 mph speed by riding his brakes until they
heated up to 600◦F and burned up. The brakes weighed 40 lbm and had a heat
capacity of 0.1 BT U=lbm ◦F. At the crest of the hill they were at 60 ◦F.
Heat was lost from the brakes to the air, as the brakes heated up, at a rate
proportional to the temperature difference between the brake temperature and
the air temperature. The proportionality constant was 30 BT U=h ◦F.
Assume that the car was frictionless and encountered negligible air resistance.
1. At was distance down the hill did Sam’s brakes burn up?
2. What speed did his car attain by the time it reached the bottom of the
hill?
Problem 16
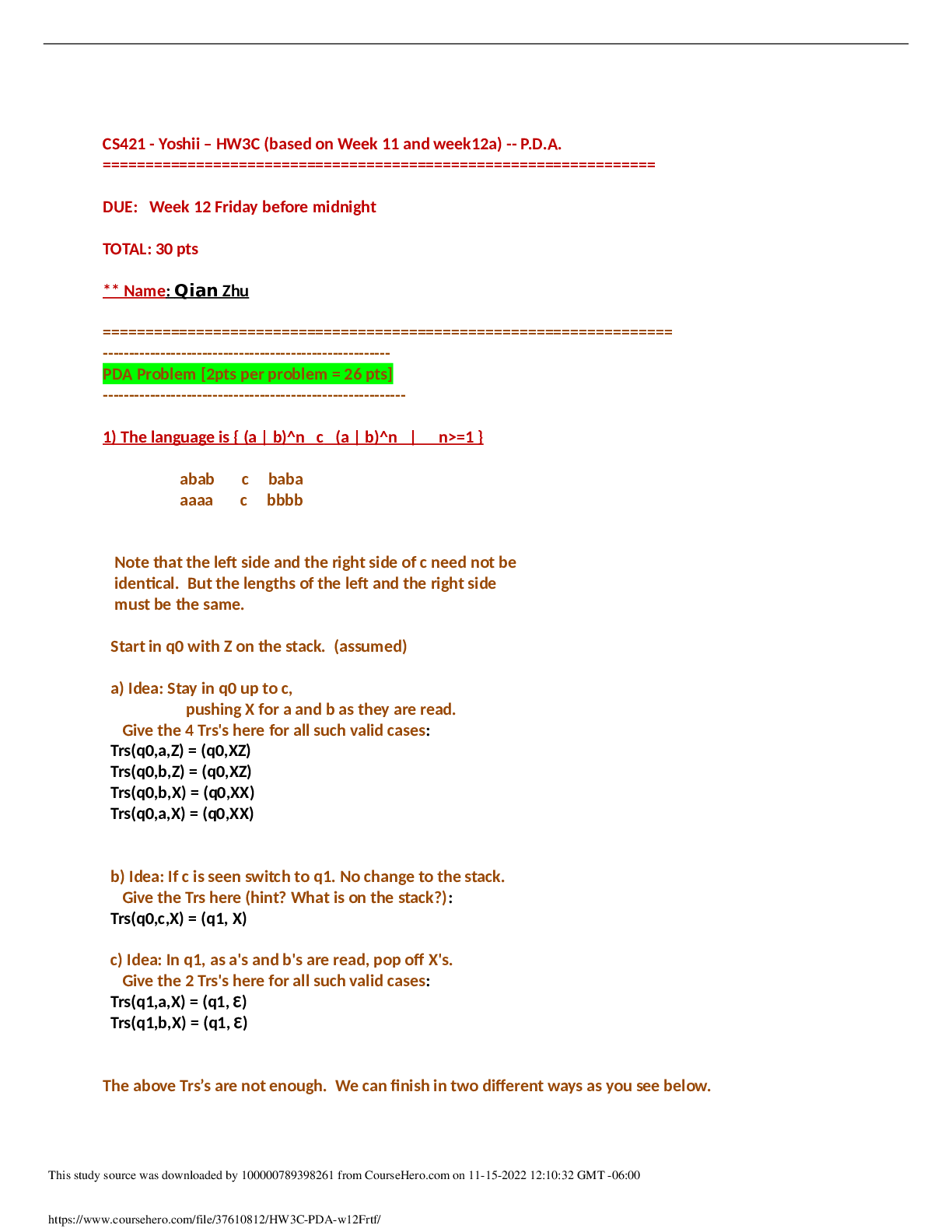
A farmer fills his silo with chopped corn (Figure 1). The entire corn plant
(leaves, stem, and ear) is cut up into small pieces and blown into the top of the
cylindrical silo at a rate W0. This is similar to a fed-batch chemical reaction
system.
The diameter of the silo is D and its height is H. The density of the chopped
corn in the silo varies with the depth of the bed. The density ρ at a point that
has z feet of material above it is:
ρ(z) = ρ0 + βz
where ρ0 and β are constants. 1. Write the equations that describe the system and show how the height of
the bed h(t) varies as a function of time.
2. What is the total weight of corn fodder that can be stored in the silo? Problem 17
Two consecutive, first-order reactions take place in a perfectly mixed, isothermal
batch reactor:
A −! k1 B −! k2 C
Assuming constant density, solve analytically for the dynamic changes in
the concentrations of components A and B in the situation where k1 = k2. The
initial concentration of A at the beginning of the batch cycle is CA0. There is
initially no B or C in the reactor.
What is the maximum concentration of component B that can be produced
and at what point in time does it occur? Problem 18
The same reactions considered in Problem 17 are now carried out in a single,
perfectly mixed, isothermal continuous reactor. Flow rates, volume and densities are constant.
1. Derive a mathematical model describing the system.
2. Solve for the dynamic change in the concentration of component A, CA,
if the concentration of A in the feed stream is constant at CA0 and the
initial concentrations of A, B and C at time equal zero are CA(0) = CA0
and CB(0) = CC(0) = 0.
3. In the situation where k1 = k2, find the value of holdup time (τ = V=F)
that maximizes the steady state ratio of CB=CA0. Compare this ratio
with the maximum found in Problem 17. Problem 19
The same consecutive reactions considered in Problem 18 are now carried out in
two perfectly mixed continuous reactors. Flow rate and densities are constant.
The volumes of the two tanks (V) are the same and constant. The reactors
operate at the same constant temperature.
1. Derive a mathematical model describing the system.
2. If k1 = k2, find the value of the hold up time (τ = V=F ) that maximizes
the steadystate ratio of concentration of component B in the product to
the concentration of reactant A in the feed Problem 20
A vertical, cylindrical tank is filled with well water at 65◦F. The tank is insulated at the top and bottom but is exposed on its vertical sides to cold 10◦F
night air. The diameter of the tank is 2 feet and its height is 3 feet. The overall
heat transfer coefficient is 20 BT U=h ◦F ft2. Neglect the metal wall of the tank
and assume that the water in the tank is perfectly mixed.
1. Calculate how many minutes it will be until the first crystal of ice is
formed.
2. How long will it take to completely freeze the water in the tank? The heat
of fusion of water is 144 BT U=lbm. Problem 21
An isothermal, first-order, liquid-phase, reversible reaction is carried out in a
constant-volume, perfectly mixed continuous reactor.
A −! k1 B
B −! k2 A
The concentration of product B is zero in the feed and in the reactor is CB.
Feed rate is F.
1. Derive a mathematical model describing the dynamic behaviour of the
system.
2. Derive the steadystate relationship between CA and CA0. Show that the
conversion of A and the yield of B decrease as k2 increases.
3. Assuming that the reactor is at this steadystate concentration and that a
step change is made in CA0 to (CA0 + ∆CA0), find the analytical solution
that gives the dynamic response of CA(t). Problem 22
An isothermal, first order, liquid phase, irreversible reaction is conducted in a
constant volume batch reactor.
A −! k1 B
The initial concentration of reactant A at the beginning of the batch is CA0.
The specific reaction rate k decreases with time because of catalyst degradation:
k = k0e−βt.
1. Solve for CA(t).
2. Show that in the limit as β ! 0, CA(t) = CA0e−k0t.
3. Show that in the limit as β ! 1, CA(t) = CA0. Problem 23
There are 3460 pounds of water in the jacket of a reactor that are initially at
145◦F. At time equal zero, 70◦F cooling water is added to the jacket at a
constant rate of 416 pounds per minute. The holdup of water in the jacket
is constant since the jacket is completely filled with water and excess water is
removed from the system on pressure control as cold water is added. Water in
the jacket can be assumed to be perfectly mixed.
1. How many minutes does it take the jacket water to reach 99◦F if no heat
is transferred into the jacket?
2. Suppose a constant 362000 BTU/h of heat is transferred into the jacket
from the reactor, starting at time equal zero when the jacket is at 145◦F.
How long will it take the jacket water to reach 99◦F if the cold water
addition rate is constant at 416 pounds per minute? Problem 24
Hay dries, after being cut, at a rate which is proportional to the amount of
moisture it contains. During a hot (90◦F) July summer day, this proportionality constant is 0.30 h−1. Hay cannot be baled until it has dried down to no
more than 5 % moisture. Higher moisture levels will cause heating and mold
formation, making it unsuitable for horses.
The effective drying hours are from 11:00 a.m. to 5:00 p.m. If hay cannot
be baled by 5.00 p.m. it must stay in the field overnight and picks up moisture
from the dew. It picks up 25 percent of the moisture that is lost during the
previous day.
If the hay is cut at 11:00 a.m. Monday morning and contains 40 wt %
moisture at the moment of cutting, when can it be baled?Problem 25
Process liquid is continuously fed into a perfectly mixed tank in which it is
heated by a steam coil. Feed rate F is 50000 lbm=h of material with a constant
density ρ of 50 lbm=ft3 and heat capacity Cp of 0.5 BT U=lbm ◦F. Holdup in
the tank V is constant at 4000 lbm. Inlet feed temperature T0 is 80 ◦F.
Steam is added at a rate S lbm=h that heats the process liquid up to temperature T. At the initial steadystate, T is 190◦F. The latent heat of vaporization
λs of the steam is 900 BT U=lbm











.png)
.png)
.png)
.png)