CH 19 - Solution Procedures for Transportation and Assignment Problems Questions and Answers

Document Content and Description Below

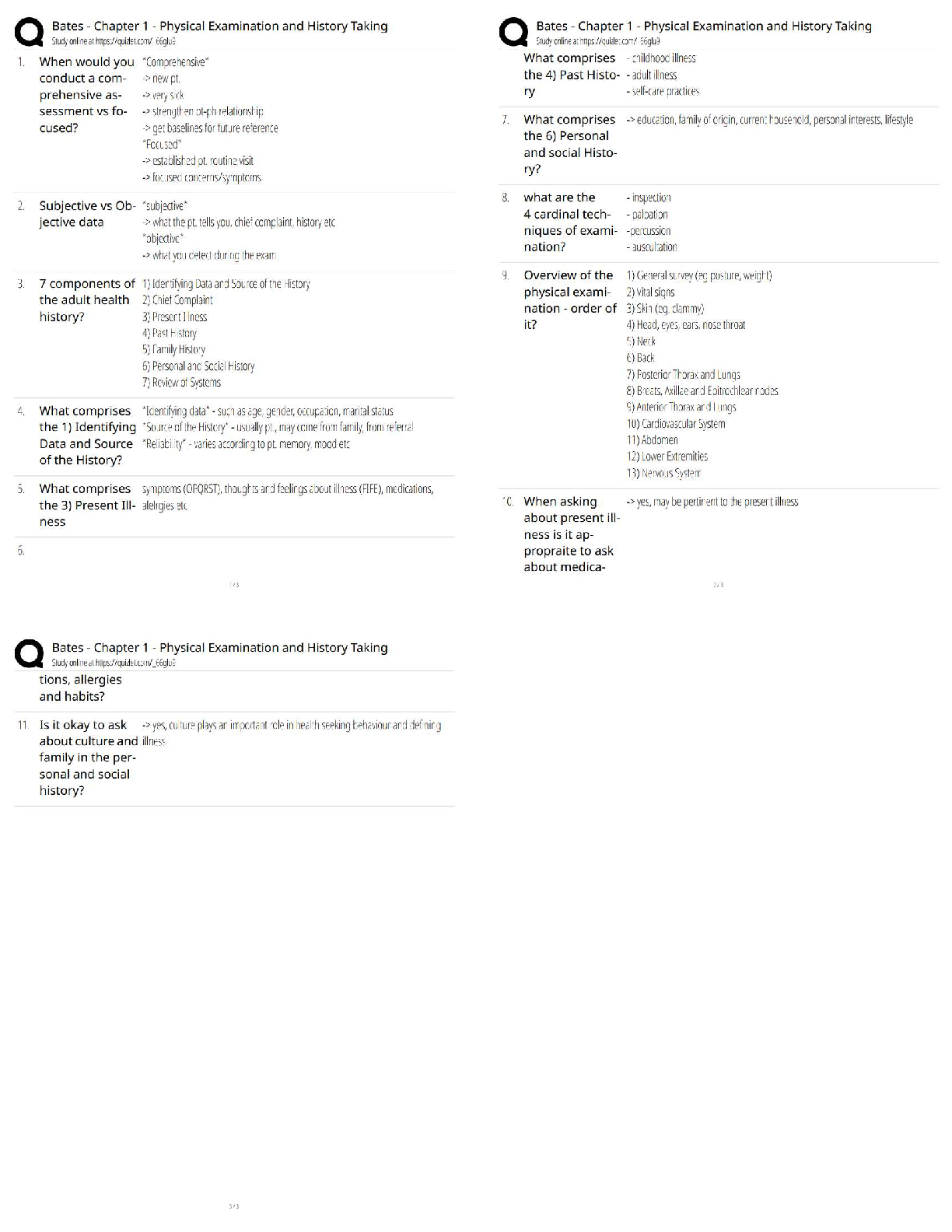
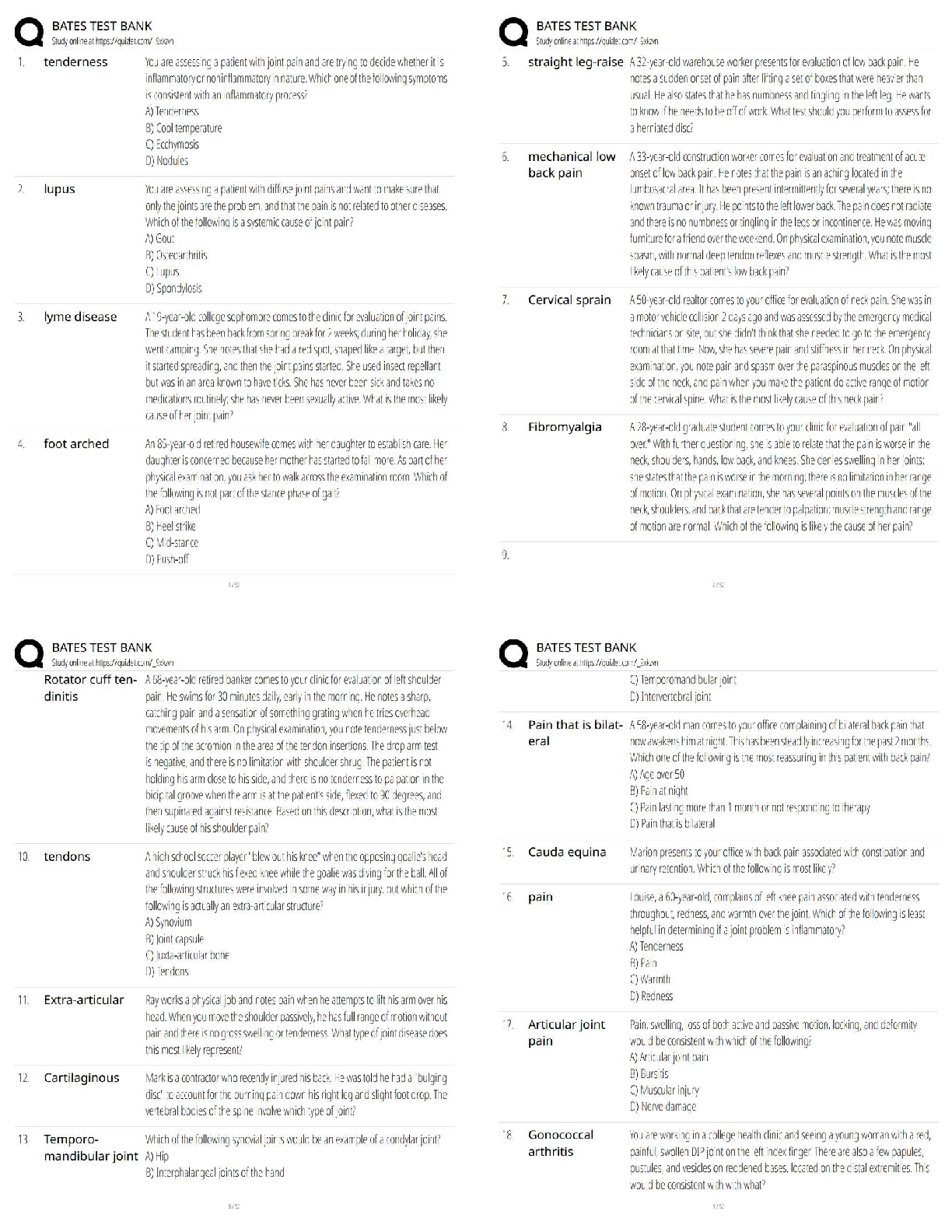
True / False 1. The transportation simplex method can be used to solve the assignment problem. a. True b. False 2. The transportation simplex method is limited to minimization proble... ms. a. True b. False 3. For an assignment problem with three agents and four tasks, the assignment matrix will have three rows and four columns. a. True b. False 4. The transportation simplex method can be applied only to a balanced problem; if a problem is not balanced, a dummy origin or dummy destination must be added. a. True b. False 5. In assignment problems, dummy agents or tasks are created when the number of agents and tasks is not equal. a. True b. False 6. The transportation simplex method is more efficient than general-purpose linear programming for solving large-sized transportation problems. a. True b. False 7. A dummy origin in a transportation problem is used when supply exceeds demand. a. True b. False 8. The net evaluation index for occupied cells in the transportation simplex method is 0. a. True b. False 9. Optimal assignments are made in the Hungarian method to cells in the reduced matrix that contain a 0. a. True b. False 10. Using the Hungarian method, the optimal solution to an assignment problem is found when the minimum number of lines required to cover the zero cells in the reduced matrix equals the number of agents. a. True b. False 11. To handle unacceptable routes in a transportation problem where cost is to be minimized, infeasible arcs must be assigned negative cost values. a. True b. False 12. The transportation simplex method is a two-phase method that first finds an initial feasible solution and then makes iterative improvements in the solution until an optimal solution is reached. a. True b. False 13. In the transportation simplex method, when total supply is greater than total demand, we introduce a dummy destination with demand less than the excess of supply over demand. a. True b. False 14. Finding an initial feasible solution can be done by using a heuristic procedure. a. True b. False Multiple Choice 15. A solution to a transportation problem that has less than m + n − 1 cells with positive allocations in the transportation tableau is a(n) a. optimal solution. b. initial feasible solution. c. minimum cost solution. d. degenerate solution. 16. The optimal solution is found in an assignment matrix when the minimum number of straight lines needed to cover all the zeros equals a. number of agents − 1. b. number of agents. c. number of agents + 1. d. number of agents + number of tasks. 17. The stepping-stone method requires that one or more artificially occupied cells with a flow of zero be created in the transportation tableau when the number of occupied cells is fewer than a. m + n − 2. b. m + n − 1. c. m + n. d. m + n + 1. 18. The per-unit change in the objective function associated with assigning flow to an unused arc in the transportation simplex method is called the a. net evaluation index. b. degenerate value. c. opportunity loss. d. simplex multiplier. 19. The difference between the transportation and assignment problems is that a. total supply must equal total demand in the transportation problem. b. the number of origins must equal the number of destinations in the transportation problem. c. each supply and demand value is 1 in the assignment problem. d. There are many differences between the transportation and assignment problems. 20. An example of a heuristic is the a. minimum cost method. b. stepping-stone method. c. Hungarian method. d. MODI method. 21. Using the transportation simplex method, the optimal solution to the transportation problem has been found when a. there is a shipment in every cell. b. more than one stepping-stone path is available. c. there is a tie for the outgoing cell. d. the net evaluation index for each unoccupied cell is ≥ 0. 22. Identifying the outgoing arc in phase II of the transportation simplex method is performed using the a. minimum cost method. b. MODI method. c. stepping-stone method. d. matrix reduction method. 23. In order to identify the arc that will cause the largest reduction per unit in the total cost of the current solution, we use the MODI method. The MODI method is used to identify a. an outgoing arc. b. an incoming arc. c. unoccupied cells. d. an initial feasible solution. 24. To use the transportation simplex method, a transportation problem that is unbalanced requires the use of a. artificial variables. b. one or more transshipment nodes. c. a dummy origin or destination. d. matrix reduction. 25. To use the Hungarian method, a profit-maximization assignment problem requires a. converting all profits to opportunity losses. b. a dummy agent or task. c. matrix expansion. d. finding the maximum number of lines to cover all the zeros in the reduced matrix. 26. To use the transportation simplex method, a. there can be no unacceptable routes. b. the initial feasible solution cannot be degenerate. c. a minimization objective function must be the case. d. total supply must equal total demand. 27. The Hungarian method involves a. matrix reduction. b. subtracting and adding appropriate values to yield an optimal solution. c. continuing iteratively until the value of one of the solutions is zero. d. All of these are correct. Subjective Short Answer 28. Develop the transportation tableau for this transportation problem. 29. Solve the following transportation problem using the transportation simplex method. State the minimum total shipping cost. Origin Supply Destination Demand A 500 X 300 B 400 Y 300 Z 300 Shipping costs are as follows: Destination Source X Y Z A 2 3 5 B 9 12 10 30. Canning Transport is to move goods from three factories (origins) to three distribution centers (destinations). Information about the move is given below. Solve the problem using the transportation simplex method and compute the total shipping cost. Origin Supply Destination Demand A 200 X 50 B 100 Y 125 C 150 Z 125 Shipping costs are as follows: Destination Origin X Y Z A 3 2 5 B 9 10 – C 5 6 4 (Source B cannot ship to destination Z.) 31. The following table shows the unit shipping cost between cities, the supply at each origin city, and the demand at each destination city. Solve this minimization problem using the transportation simplex method and compute the optimal total cost. Destination Origin Terre Haute Indianapolis Ft. Wayne South Bend Supply St. Louis 8 6 12 9 100 Evansville 5 5 10 8 100 Bloomington 3 2 9 10 100 Demand 150 60 45 45 32. After some special presentations, the employees of the AV Center have to move overhead projectors back to classrooms. The table below indicates the buildings where the projectors are now (the origins), where they need to go (the destinations), and a measure of the distance between sites. Determine the transport arrangement that minimizes the total transport distance. Destination Origin Business Education Parsons Hall Holmstedt Hall Supply Baker Hall 10 9 5 2 35 Tirey Hall 12 11 1 6 10 Arena 15 14 7 6 20 Demand 12 20 10 10 33. Solve the following assignment problem using the Hungarian method. No agent can be assigned to more than one task. Total cost is to be minimized. Task Agent A B C D 1 9 5 4 2 2 12 6 3 5 3 11 6 5 7 34. Use the Hungarian method to obtain the optimal solution to the following assignment problem in which total cost is to be minimized. All tasks must be assigned, and no agent can be assigned to more than one task. Task Agent A B C D 1 10 12 15 25 2 11 14 19 32 3 18 21 23 29 4 15 20 26 28 35. A professor has been contacted by four not-for-profit agencies that are willing to work with student consulting teams. The agencies need help with such things as budgeting, information systems, coordinating volunteers, and forecasting. Although each of the four student teams could work with any of the agencies, the professor feels that there is a difference in the amount of time it would take each group to solve each problem. The professor's estimate of the time, in days, is given in the table below. Use the Hungarian method to determine which team works with which project. All projects must be assigned, and no team can be assigned to more than one project. Project Team Budgeting Information Volunteers Forecasting A 32 35 15 27 B 38 40 18 35 C 41 42 25 38 D 45 45 30 42 36. A manufacturer of electrical consumer products, with its headquarters in Burlington, Iowa, produces electric irons at Manufacturing Plants 1, 2, and 3. The irons are shipped to Warehouses A, B, C, and D. The shipping cost per iron, the monthly warehouse requirements, and the monthly plant production levels are as follows: Warehouse Monthly Plant Production (units) A B C D Plant 1 $0.20 $0.25 $0.15 $0.20 10,000 Plant 2 0.15 0.30 0.20 0.15 20,000 Plant 3 0.15 0.20 0.20 0.25 10,000 Monthly warehouse requirements (units) 12,000 8000 15,000 5000 How many electric irons should be shipped per month from each plant to each warehouse to minimize monthly shipping costs? a. Use the minimum cost method to find an initial feasible solution. b. Can the initial solution be improved? c. Compute the optimal total shipping cost per month. 37. Al Bergman, staff traffic analyst at the corporate headquarters of Computer Products Corporation (CPC), is developing a monthly shipping plan for the El Paso and Atlanta manufacturing plants to follow next year. These plants manufacture specialized computer workstations that are shipped to five regional warehouses. Al has developed the following estimated requirements and costs: Warehouse Monthly Plant Production (units) Plant Chicago Dallas Denver New York San Jose Atlanta $35 $40 $60 $45 $90 200 El Paso 50 30 35 95 40 300 Monthly warehouse requirements (units) 75 100 25 150 150 a. Use the minimum cost method to find an initial feasible solution. b. Use the transportation simplex method to find an optimal solution. c. Compute the optimal total shipping cost. 38. Consider the transportation problem below. Destination Supply Origin 1 2 3 A $0.50 $0.90 $0.50 100 B 0.80 1.00 0.40 500 C 0.90 0.70 0.80 900 Demand 300 800 400 a. Use the minimum cost method to find an initial feasible solution. b. Can the initial solution be improved? c. Compute the optimal total shipping cost. 39. Five customers needing their tax returns prepared must be assigned to five tax accountants. The estimated profits for all possible assignments are shown below. Only one accountant can be assigned to a customer, and all customers' tax returns must be prepared. What should the customer–accountant assignments be so that estimated total profit is maximized? What is the resulting total profit? Accountant Customer 1 2 3 4 5 A $500 $525 $550 $600 $700 B 625 575 700 550 800 C 825 650 450 750 775 D 590 650 525 690 750 E 450 750 660 390 550 40. Four jobs must be assigned to four work centers. Only one job can be assigned to each work center, and all jobs must be processed. The cost of processing each job at each work center is shown below. Determine which jobs should be assigned to which work center to minimize total processing cost. Compute the total processing cost. Work Center Job 1 2 3 4 A $50 $45 $50 $65 B 25 40 35 20 C 65 60 55 65 E 55 65 75 85 41. Four employees must be assigned to four projects. Only one employee can be assigned to each project, and all projects must be completed. The cost of each employee completing each project is shown below. Determine which employee should be assigned to which project to minimize total project completion cost. Be sure to compute the total project completion cost. Project Employee 1 2 3 4 Al $300 $325 $500 $350 Ben 400 525 575 600 Cal 350 400 600 500 Dan 400 350 450 450 42. A large screen printer is faced with six jobs due on Tuesday. The plan is to do the jobs on Monday so they will be ready on time. The shop has six worker-machine pairs that can work on any of the six jobs. Because of differing experience levels and machine capabilities, processing times differ. The processing times presented in the table below are in minutes. What is the optimal assignment of jobs to worker-machine pairs that minimizes total processing time? Worker-Machine Pair Job 1 2 3 4 5 6 A 250 375 175 425 225 350 B 350 310 375 410 275 225 C 410 450 325 275 315 275 D 380 245 350 375 210 350 E 395 250 280 390 410 375 F 250 285 410 385 300 295 43. A company ships products from four factories to four warehouses. The factory capacities, warehouse requirements, and per-unit shipping costs are shown below. Warehouse Monthly Factory Capacity (units) 1 2 3 4 Factory A $11 $13 $ 9 $ 6 5000 Factory B 12 10 7 9 10,000 Factory C 19 16 15 21 10,000 Factory D 7 6 4 9 5000 Monthly warehouse requirement (units) 3000 8000 12,000 5000 How many products should the company ship from each factory to each warehouse to minimize monthly shipping costs? What will the monthly shipping cost be if the shipping plan is followed? (Use the minimum cost method to find an initial feasible solution and the transportation simplex method to find an optimal solution.) 44. The Des Moines plant of Tri-B Corp. has three fabrication departments with each producing a single unique product with equipment that is dedicated solely to its product. The three products are moved to four assembly departments where they are assembled. Although any of the three products can be processed in any of the assembly departments, the materials handling and assembly costs are different because of the varying distances between departments and because of different equipment. Each fabrication and assembly department has a different monthly capacity, and it is desirable that each department operate at capacity. The variable costs and capacity for each department are shown below. Assembly Department Monthly Fabrication Dept. Capacity (units) 1 2 3 4 Fabrication Dept. A $1.20 $0.70 $0.50 $0.60 9000 Fabrication Dept. B 0.70 0.50 0.50 0.60 17,000 Fabrication Dept. C 0.50 0.70 0.80 1.20 14,000 Monthly assembly dept. capacity (units) 3000 10,000 15,000 12,000 How many units of each product should be moved from each fabrication department to each assembly department to minimize total monthly costs? (Use the minimum cost method to find an initial feasible solution and the transportation simplex method to find an optimal solution.) Compute the optimal total monthly cost. [Show More]

Last updated: 2 years ago

Preview 1 out of 20 pages