MATH 221 Final Exam study guide solutions | Highly Rated Paper | Download To Score An A+

Document Content and Description Below

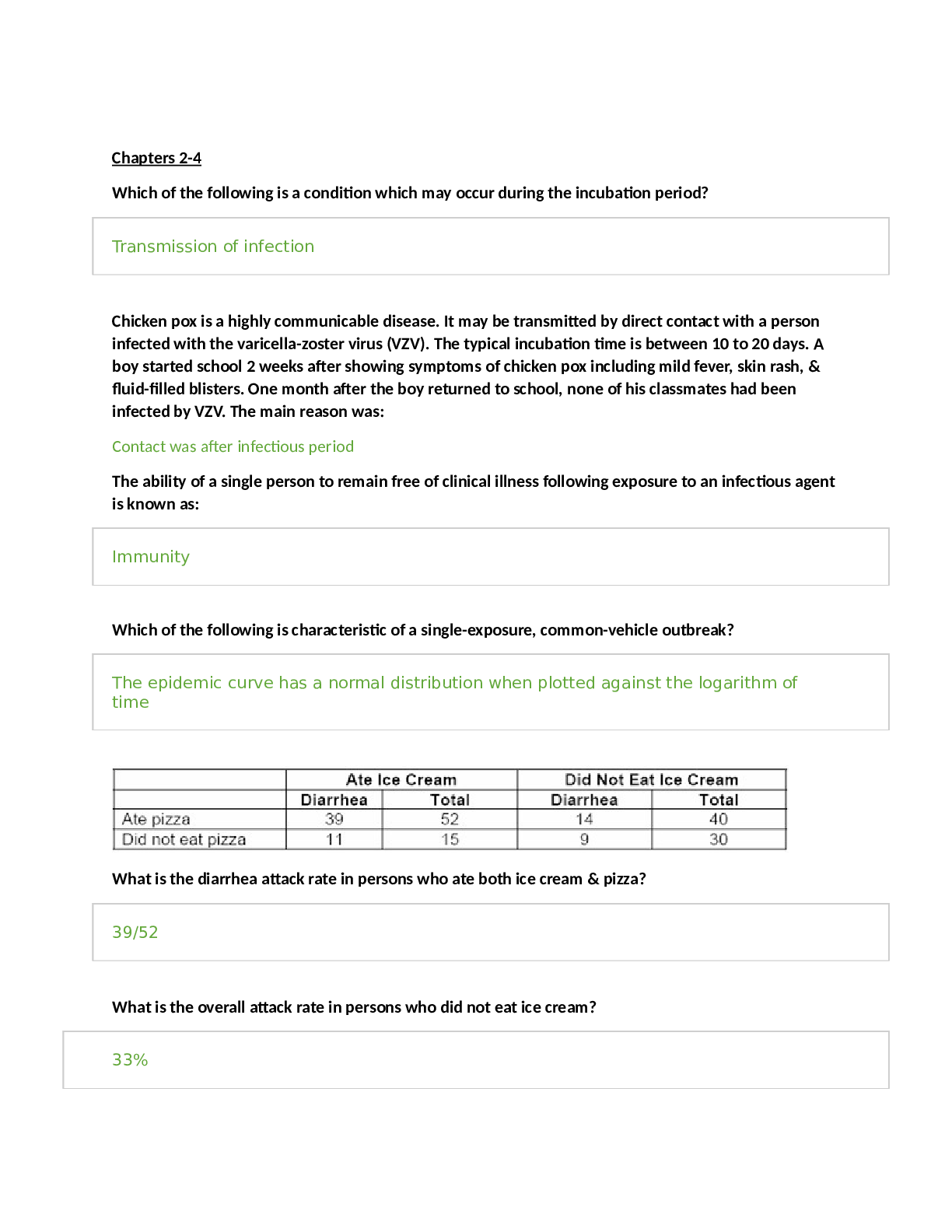
Final Exam Review Questions – MATH221 You should work each of the following on your own, then review the solutions guide. DO NOT look at the solutions guide first. 1. Determine whether the foll... owing are nominal, ordinal, interval, and ratio. a. Daily temperatures in Ripon, WI b. Test scores in statistics class Solution: (a) would be interval as there is no zero while (b) would be ratio as there is a zero. 2. The following numbers represent the weights in pounds of six 7-year old children in Mrs. Jones' 2nd grade class. {25, 60, 51, 47, 49, 45} Find the mean; median; mode; variance; standard deviation. Solution: This would be a sample from the class mean = 46.166 (=AVERAGE) median = 48 (=MEDIAN) mode does not exist (looking at the data) variance = 134.5667 (=VARIANCE.S) standard deviation =11.60029 (=STDEV.S) 3. If the variance is 846, what is the standard deviation? Solution: standard deviation = square root of variance = sqrt(846) = 29.086 4. If we have the following data: 34, 38, 22, 21, 29, 37, 40, 41, 22, 20, 49, 47, 20, 31, 34, 66. Draw a stem and leaf. Discuss the shape of the distribution. Solution: 2 | 2 1 9 2 0 0 3 | 4 8 7 1 4 4 | 0 1 9 7 5 | 6 | 6 This distribution is right skewed (positively skewed) because the “tail” extends to the right. 5. Find the regression equation of the following data. X 6 5 7 6 5 6 8 9 4 y 14 33 43 54 21 33 43 24 28 Solution: y-hat = 1.32x + 24.32, found by using Data and then Data Analysis menu option. 6. To predict the annual rice yield in pounds we use the equation y-hat = 859 + 5.76x1 + 3.82x2 where x1 represents the number of acres planted and where x2 represents the number of acres harvested and where r2 = 0.94. a. Predict the annual yield when 3200 acres are planted and 3000 are harvested b. Interpret the results of r2 value. Solution: (a) y-hat = 859 + 5.76*3200 + 3.82*3000 = 859 + 18432 + 11460 = 30751 which is 30,751 pounds of rice (b) 94% of the variation in the annual rice yield can be explained by the number of acres planted and harvested. The remaining 6% is unexplained and is due to other factors or to chance. 7. The Student Services office did a survey of 500 students with the following results: Transfer Non-transfer Total Part-time 100 110 210 Full-time 170 120 290 Total 270 230 500 a. Find the probabilities that a student is a transfer student. b. Find the probability that a students is part-time. c. Find the probability that a student is a transfer student and a part-time student d. Find the probability that a student is a transfer student, given that the student is part-time, P(transfer|part-time). Solution: (a) The total number of transfer students is 270. The total number of students in the survey is 500. P(Transfer) = 270/500 = .54 (b) The total number of part time students is 210. The total number of students in the survey is 500. P(Part Time) = 210/500 = .42 (c) From the table we see that there are 100 students which are both transfer and part time. This is out of 500 students in the sample. So, 100/500 = .20 (d) This is conditional probability and so we must change the denominator to the total of what has already happened. There are 100 students which are both transfer and part time. There are 210 part time students. P(transfer | part time) = 100/210 ≈ .4762. 8. A shipment of 40 television sets contains 3 defective units. How many ways can a vending company can buy five of these units and receive no defective units? Solution: There are 37 sets which are not defective. There are 37C5 ways to get 5 sets with none defective. 37C5 = 435, 897. In Excel, it would be =COMBIN(37,5). Thus, there are 435,897 ways to get 5 sets with non- defective. 9. The mean number of cars per minute going through the Eisenhower turnpike automatic toll is about 7. Find the probability that exactly 3 will go through in a given minute using the correct table, formula, or Excel function. Solution: =poisson.dist(3,7,FALSE) to get 0.0521 or about 5%. 10. A company claims that 61% of consumers know about their product. If the company asks 18 consumers, what is the probability that (a) exactly 10 will say yes, that (b) between 10 and 12 will say yes. Solution: For part A, it would be =BINOM.DIST(10,18,0.61,FALSE) to get 0.167 or 16.7%. For part B, it would be =BINOM.DIST(12,18,0.61,TRUE)- BINOM.DIST(10,18,0.61,TRUE) to get 0.3634 or about 36%. 11. On a dry surface, the braking distance (in meters) of a certain car is a normal distribution with mu = μ = 45.1 m and sigma = σ = 0.5 a. Find the braking distance that represents the 91st percentile. b. Find the probability that the braking distance is less than or equal to 45 m c. Find the probability that the braking distance is greater than 46.8 m d. Find the probability that the braking distance is between 45 m and 46.8 m. Solution: (a) =NORM.INV(0.91, 45.1, 0.5) to get 45.77m. (b) =NORM.DIST(45, 45.1, 0.5, TRUE) to get 0.4207. (c) Find the probability of less than 46.8 first and then subtract that probability from 1. So it would be =NORM.DIST(46.8, 45.1, 0.5, TRUE) which is 0.99966. More than 46.8 would be 1 - 0.99966 = 0.00034. (d) Find the probability of each and subtract the larger from the smaller. In one cell, =NORM.DIST(46.8, 45.1, 0.5, TRUE) – NORM.DIST(45, 45.1, 0.5, TRUE) to get 0.579. 12. A sample of 58 days of gas prices has a mean of $2.75 and a standard deviation of $0.86. Construct the 95% confidence interval. Solution: In Excel, find E and then add and subtract that from the mean of 2.75. In Excel, type =CONFIDENCE.NORM(0.05, 0.86, 58) which works out to 0.22. The interval would be (2.75-0.22, 2.75 + 0.22) or (2.53, 2.97). 13.A A drug manufacturer wants to estimate the mean heart rate for patients with a certain heart condition. Because the condition is rare, the manufacturer can only find 14 people with the condition currently untreated. From this small sample, the mean heart rate is 101 beats per minute with a standard deviation of 8. a. Find a 99% confidence interval for the true mean heart rate of all people with this untreated condition. Show your calculations. b. Interpret this confidence interval and write a sentence that explains it. Solution: Since this is a small sample, need to first find tc and then find the maximum error. Tc = T.INV((1-0.99)/2, 13) = -3.01 Maximum error = -3.01(8/sqrt(14)) = -6.44 Then find the confidence interval by adding and subtracting from the mean (101 – 6.44 , 101 + 6.44) (94.56, 107.44) This means that we are 99% confident that the true population mean falls between 94.56 and 107.44. 14. Determine the minimum required sample size if you want to be 80% confident that the sample mean is within 2 units of the population mean given sigma = 9.4. Assume the population is normally distributed. Solution: n = (Zc*sigma/E)^2 = [(1.28 * 9.4)/ 2]^2 = (6.016)^2 = 36.192256 = 37 rounded up. (We always round up to the next whole number.) 15. If a sample of 15 employees worked an average of 42.8 hours in the week with a standard deviation of 2.3, what would be the 99% confidence interval for the hours worked? Solution: This is a 99% small sample confidence interval. First find the tc and then find the maximum error. Tc = T.INV((1-0.99)/2, 14) = -2.98 Maximum error = -2.98(2.3/sqrt(15)) = -1.77 Confidence interval is then (42.8 – 1.77, 42.8 + 1.77) (41.03, 44.57) 16.A A social service worker wants to estimate the true proportion of pregnant teenagers who miss at least one day of school per week on average. The social worker wants to be within 5% of the true proportion when using a 90% confidence interval. A previous study estimated the population proportion at 0.21. a. Using this previous study as an estimate for p, what sample size should be used? b. If the previous study was not available, what estimate for p should be used? Solution: (a). The critical z-value for a 90% confidence interval is 1.645. Since a previous study is known, we can use it to estimate p = 0.21. The maximum error is 0.05. Sample size = n = p*(1-p)*( z / error )^2 = 0.21*(0.79)*(1.645/0.05)^2 = 179.5718 = 180 rounded up Thus, at least 180 pregnant teenagers must be sampled. (b). If no estimate of p is known, we must use p = 0.5 to have a large enough sample size to meet the desired maximum error. = 0.50*(0.50)*(1.645/0.05)^2 = 270.6 which would be 271 when rounded up. 17. A restaurant claims that its speed of service time is less than 15 minutes. A random selection of 49 service times was collected, and their mean was calculated to be 14.5 minutes. Their standard deviation is 2.7 minutes. Is there enough evidence to support the claim at alpha = .07? Write the hypotheses, the p-value, conclusion, and implication for the claim. Solution: Ho: mu ≥ 15 min. Ha: mu < 15 min. (claim). Therefore, it is a left-tailed test. n=49; x-bar=14.5; s=2.7; alpha=0.07 To find the area to the left: =NORM.DIST(14.5,15,2.7/SQRT(49),TRUE) = 0.097 Since it is left-tailed, we can leave as it is for the p-value. Since p-value = .097 > .07 = alpha, we do not reject Ho. The implication is that the restaurant can NOT say that its service is less than 15 minutes. 18. To support their claim that the average speed on their road is more than 25 mph, neighbors collect data on 24 cars on a day. Those cars have a mean speed of 26.7mph and a standard deviation of 3.9mph. Do the neighbors have enough information to support their claim at an alpha of 0.05? Write the hypotheses, the p-value, conclusion, and implication for the claim. Solution: Ho: u <= 25 Hz: u > 25 (claim) Right-tailed test Test statistic for this small sample hypothesis test would be = (26.7-25)/(3.9/sqrt(24)) = 2.135 p-value based on this test statistic =1 – T.DIST(2.135,23,TRUE) = 0.022 Since p-value = 0.022 < 0.05, we can reject Ho. The implication is that the claim is supported by the evidence. 19. A doctor claims that 30% of patients only have a cold. During one month, the doctor finds that 112 of 420 patients only has a cold. At α=0.06, can the doctor support the claim? Write the hypotheses, the p-value, conclusion, and implication for the claim. Solution: Ho: p = 0.30 (claim) Ha: p ≠ 0.30. Therefore, it is a two-tailed proportion test. n=420; x=112; alpha=0.06; based on this p-hat=112/420=0.267 and q- hat = 1-0.267 = 0.733. To find the area to the left: =NORM.DIST((0.266667-0.3)/sqrt(0.3*0.7/420),0,1,TRUE) = 0.068 Since it is two-tailed, we multiply this by 2 for the p-value, 2*0.068 = 0.136 Since p-value = .136 > .06 = alpha, we do not reject Ho. The implication is that the doctor can claim that 30% of patients have a cold. [Show More]

Last updated: 2 years ago

Preview 1 out of 6 pages