Calculus > QUESTIONS & ANSWERS > Chapter 3: DIFFERENTIATION RULES. Work And Answers (All)
Chapter 3: DIFFERENTIATION RULES. Work And Answers
Document Content and Description Below
3.1 Derivatives of Polynomials and Exponential Functions 1. (a) is the number such that lim →0 − 1 = 1. (b) 27 − 1 −0001 09928 −00001 09 ... 932 0001 09937 00001 09933 28 − 1 −0001 10291 −00001 10296 0001 10301 00001 10297 From the tables (to two decimal places), lim →0 27 − 1 = 099 and lim →0 28− 1 = 103. Since 099 1 103, 27 28. 2. (a) The function value at = 0 is 1 and the slope at = 0 is 1. (b) () = is an exponential function and () = is a power function. () = and () = −1. (c) () = grows more rapidly than () = when is large. 3. () = 240 is a constant function, so its derivative is 0, that is, 0() = 0. 4. () = 5 is a constant function, so its derivative is 0, that is, 0() = 0. 5. () = 52 + 23 ⇒ 0() = 52(1) + 0 = 52 6. () = 7 42 − 3 + 12 ⇒ 0() = 7 4(2) − 3(1) + 0 = 7 2 − 3 7. () = 23 − 32 − 4 ⇒ 0() = 2(32) − 3(2) − 4(1) = 62 − 6 − 4 8. () = 145 − 252 + 67 ⇒ 0() = 14(54) − 25(2) + 0 = 74 − 5 9. () = 2(1 − 2) = 2 − 23 ⇒ 0() = 2 − 2(32) = 2 − 62 10. () = (3 − 1)( + 2) = 32 + 5 − 2 ⇒ 0() = 3(2) + 5(1) − 0 = 6 + 5 11. () = 2−34 ⇒ 0() = 2− 3 4−74 = − 3 2−74 12. () = −6 ⇒ 0() = (−6−7) = −6−7 13. () = 5 3 = 5−3 ⇒ 0() = 5(−3−4) = −15−4 = −15 4 14. = 53 − 23 ⇒ 0 = 5 323 − 2 3−13 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. 167 NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.168 ¤ CHAPTER 3 DIFFERENTIATION RULES 15. () = (3 + 1)2 = 92 + 6 + 1 ⇒ 0() = 9(2) + 6(1) + 0 = 18 + 6 16. () = √4 − 4 = 14 − 4 ⇒ 0() = 1 4−34 − 4() = 1 4−34 − 4 17. () = √ − = 12 − ⇒ 0() = 1 2−12 − 1 or 2√1 − 1 18. = √3 (2 + ) = 213 + 43 ⇒ 0 = 2 1 3−23 + 4 313 = 2 3−23 + 4 313 or 3√322 + 43 √3 19. = 3 + √34 = 3 + 4−13 ⇒ 0 = 3() + 4(− 1 3)−43 = 3 − 4 3−43 20. () = 42 ⇒ 0() = 4(2) = 8 21. () = 3 + 2 + ⇒ 0() = (32) + (2) + (1) = 32 + 2 + 22. = √ + 2 = √ 2 + 2 = 12−2 + 1−2 = −32 + −1 ⇒ 0 = − 3 2−52 + (−1−2) = − 3 2−52 − −2 23. = 2 + 4 √ + 3 = 32 + 412 + 3−12 ⇒ 0 = 3 212 + 4 1 2−12 + 3− 1 2−32 = 3 2 √ + √2 − 23√ note that 32 = 22 · 12 = √ The last expression can be written as 32 2 √ + 4 2 √ − 3 2 √ = 32 + 4 − 3 2 √ . 24. () = √5 + √7 = √5 12 + √7 −1 ⇒ 0() = √5 1 2−12 + √7 −1−2 = 2√√5 − √27 25. () = 24 + 24 ⇒ 0() = 2414 + 0 = 2414 26. () = + ⇒ 0() = + −1 27. () = 1 + −12 = 1 + 2−1 + −2 ⇒ 0() = 0 + 2(−1−2) + (−2−3) = −2−2 − 2−3 28. () = + + 2 2 = 2 + 2 + 2 2 = −2 + −1 + ⇒ 0() = (−2−3) + (−1−2) + 0 = −2−3 − −2 = −2 3 − 2 or − 2 + 3 29. () = √3 − 2 = √3 − 2 = −23 − 2 ⇒ 0() = − 2 3−53 − 2 30. () = 1 + 162 (4)3 = 1 + 162 643 = 1 64−3 + 1 4−1 ⇒ 0() = 64 1 (−3−4) + 1 4(−1−2) = − 64 3 −4 − 1 4−2 or −6434 − 412 31. = 10 + = −10 + ⇒ 0 = −10−11 + = −10 11 + 32. = +1 + 1 = 1 + 1 = · + 1 ⇒ 0 = · = +1 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.1 DERIVATIVES OF POLYNOMIALS AND EXPONENTIAL FUNCTIONS ¤ 169 33. = 23 − 2 + 2 ⇒ 0 = 62 − 2. At (1 3), 0 = 6(1)2 − 2(1) = 4 and an equation of the tangent line is − 3 = 4( − 1) or = 4 − 1. 34. = 2 + ⇒ 0 = 2 + 1. At (0 2), 0 = 20 + 1 = 3 and an equation of the tangent line is − 2 = 3( − 0) or = 3 + 2. 35. = + 2 = + 2−1 ⇒ 0 = 1 − 2−2. At (2 3), 0 = 1 − 2(2)−2 = 1 2 and an equation of the tangent line is − 3 = 1 2( − 2) or = 1 2 + 2. 36. = √4 − = 14 − ⇒ 0 = 1 4−34 − 1 = 1 4√4 3 − 1. At (1 0), 0 = 1 4 − 1 = − 3 4 and an equation of the tangent line is − 0 = − 3 4( − 1) or = − 3 4 + 3 4. 37. = 4 + 2 ⇒ 0 = 43 + 2. At (0 2), 0 = 2 and an equation of the tangent line is − 2 = 2( − 0) or = 2 + 2. The slope of the normal line is − 1 2 (the negative reciprocal of 2) and an equation of the normal line is − 2 = − 1 2( − 0) or = − 1 2 + 2. 38. 2 = 3 ⇒ = 32 [since and are positive at (1 1)] ⇒ 0 = 3 212. At (1 1), 0 = 3 2 and an equation of the tangent line is − 1 = 3 2( − 1) or = 3 2 − 1 2. The slope of the normal line is − 2 3 the negative reciprocal of 3 2 and an equation of the normal line is − 1 = − 2 3( − 1) or = − 2 3 + 5 3. 39. = 32 − 3 ⇒ 0 = 6 − 32. At (1 2), 0 = 6 − 3 = 3, so an equation of the tangent line is − 2 = 3( − 1) or = 3 − 1. 40. = − √ ⇒ 0 = 1 − 1 2−12 = 1 − 1 2 √ . At (1 0), 0 = 1 2, so an equation of the tangent line is − 0 = 1 2( − 1) or = 1 2 − 1 2. 41. () = 4 − 23 + 2 ⇒ 0() = 43 − 62 + 2 Note that 0() = 0 when has a horizontal tangent, 0 is positive when is increasing, and 0 is negative when is decreasing. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.170 ¤ CHAPTER 3 DIFFERENTIATION RULES 42. () = 5 − 23 + − 1 ⇒ 0() = 54 − 62 + 1 Note that 0() = 0 when has a horizontal tangent, 0 is positive when is increasing, and 0 is negative when is decreasing. 43. (a) (b) From the graph in part (a), it appears that 0 is zero at 1 ≈ −125, 2 ≈ 05, and 3 ≈ 3. The slopes are negative (so 0 is negative) on (−∞ 1) and (2 3). The slopes are positive (so 0 is positive) on (1 2) and (3 ∞). (c) () = 4 − 33 − 62 + 7 + 30 ⇒ 0() = 43 − 92 − 12 + 7 44. (a) (b) From the graph in part (a), it appears that 0 is zero at 1 ≈ 02 and 2 ≈ 28. The slopes are positive (so 0 is positive) on (−∞ 1) and (2 ∞). The slopes are negative (so 0 is negative) on (1 2). (c) () = − 32 ⇒ 0() = − 6 45. () = 00015 − 0023 ⇒ 0() = 00054 − 0062 ⇒ 00() = 0023 − 012 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.1 DERIVATIVES OF POLYNOMIALS AND EXPONENTIAL FUNCTIONS ¤ 171 46. () = √ + √3 ⇒ 0() = 1 2−12 + 1 3−23 ⇒ 00() = − 1 4−32 − 2 9−53 47. () = 2 − 534 ⇒ 0() = 2 − 15 4 −14 ⇒ 00() = 15 16−54 Note that 0 is negative when is decreasing and positive when is increasing. 00 is always positive since 0 is always increasing. 48. () = − 3 ⇒ 0() = − 32 ⇒ 00() = − 6 Note that 0() = 0 when has a horizontal tangent and that 00() = 0 when 0 has a horizontal tangent. 49. (a) = 3 − 3 ⇒ () = 0() = 32 − 3 ⇒ () = 0() = 6 (b) (2) = 6(2) = 12 ms2 (c) () = 32 − 3 = 0 when 2 = 1, that is, = 1 [ ≥ 0] and (1) = 6 ms2. 50. (a) = 4 − 23 + 2 − ⇒ () = 0() = 43 − 62 + 2 − 1 ⇒ () = 0() = 122 − 12 + 2 (c) (b) (1) = 12(1)2 − 12(1) + 2 = 2 m s2 51. = 001553 − 03722 + 395 + 121 ⇒ = 004652 − 0744 + 395, so =12 = 00465(12)2 − 0744(12) + 395 = 1718. The derivative is the instantaneous rate of change of the length of an Alaskan rockfish with respect to its age when its age is 12 years. 52. () = 08820842 ⇒ 0() = 0882(0842−0158) = 0742644−0158, so 0(100) = 0742644(100)−0158 ≈ 036. The derivative is the instantaneous rate of change of the number of tree species with respect to area. Its units are number of species per square meter. 53. (a) = and = 50 when = 0106, so = = 50(0106) = 53. Thus, = 53 and = 53. (b) = 53 −1 ⇒ = 53(−1 −2) = −532 . When = 50, = −50 532 = −000212. The derivative is the instantaneous rate of change of the volume with respect to the pressure at 25 ◦C. Its units are m3kPa. 54. (a) = 2 + + , where ≈ −0275428, ≈ 1974853, and ≈ −27355234. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.172 ¤ CHAPTER 3 DIFFERENTIATION RULES (b) = 2 + . When = 30, ≈ 32, and when = 40, ≈ −23. The derivative is the instantaneous rate of change of tire life with respect to pressure. Its units are (thousands of miles)(lbin2). When is positive, tire life is increasing, and when 0, tire life is decreasing. 55. The curve = 23 + 32 − 12 + 1 has a horizontal tangent when 0 = 62 + 6 − 12 = 0 ⇔ 6(2 + − 2) = 0 ⇔ 6( + 2)( − 1) = 0 ⇔ = −2 or = 1. The points on the curve are (−2 21) and (1 −6). 56. () = − 2 ⇒ 0() = − 2. 0() = 0 ⇒ = 2 ⇒ = ln 2, so has a horizontal tangent when = ln 2 57. = 2 + 3 + 53 ⇒ 0 = 2 + 3 + 152. Since 2 0 and 152 ≥ 0, we must have 0 0 + 3 + 0 = 3, so no tangent line can have slope 2. 58. = 4 + 1 ⇒ 0 = 43. The slope of the line 32 − = 15 (or = 32 − 15) is 32, so the slope of any line parallel to it is also 32. Thus, 0 = 32 ⇔ 43 = 32 ⇔ 3 = 8 ⇔ = 2, which is the -coordinate of the point on the curve at which the slope is 32. The -coordinate is 24 + 1 = 17, so an equation of the tangent line is − 17 = 32( − 2) or = 32 − 47. 59. The slope of the line 3 − = 15 (or = 3 − 15) is 3, so the slope of both tangent lines to the curve is 3. = 3 − 32 + 3 − 3 ⇒ 0 = 32 − 6 + 3 = 3(2 − 2 + 1) = 3( − 1)2. Thus, 3( − 1)2 = 3 ⇒ ( − 1)2 = 1 ⇒ − 1 = ±1 ⇒ = 0 or 2, which are the -coordinates at which the tangent lines have slope 3. The points on the curve are (0 −3) and (2 −1), so the tangent line equations are − (−3) = 3( − 0) or = 3 − 3 and − (−1) = 3( − 2) or = 3 − 7. 60. The slope of = 1 + 2 − 3 is given by = 0 = 2 − 3. The slope of 3 − = 5 ⇔ = 3 − 5 is 3. = 3 ⇒ 2 − 3 = 3 ⇒ = 3 ⇒ = ln 3. This occurs at the point (ln 3 7 − 3 ln 3) ≈ (11 37). 61. The slope of = √ is given by = 1 2−12 = 1 2√. The slope of 2 + = 1 (or = −2 + 1) is −2, so the desired normal line must have slope −2, and hence, the tangent line to the curve must have slope 1 2. This occurs if 1 2√ = 1 2 ⇒ √ = 1 ⇒ = 1. When = 1, = √1 = 1, and an equation of the normal line is − 1 = −2( − 1) or = −2 + 3. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.1 DERIVATIVES OF POLYNOMIALS AND EXPONENTIAL FUNCTIONS ¤ 173 62. = () = 2 − 1 ⇒ 0() = 2. So 0(−1) = −2, and the slope of the normal line is 1 2. The equation of the normal line at (−1 0) is − 0 = 1 2[ − (−1)] or = 1 2 + 1 2. Substituting this into the equation of the parabola, we obtain 1 2 + 1 2 = 2 − 1 ⇔ + 1 = 22 − 2 ⇔ 22 − − 3 = 0 ⇔ (2 − 3)( + 1) = 0 ⇔ = 3 2 or −1. Substituting 3 2 into the equation of the normal line gives us = 5 4. Thus, the second point of intersection is 3 2 5 4, as shown in the sketch. 63. Let 2 be a point on the parabola at which the tangent line passes through the point (0 −4). The tangent line has slope 2 and equation − (−4) = 2( − 0) ⇔ = 2 − 4. Since 2 also lies on the line, 2 = 2() − 4, or 2 = 4. So = ±2 and the points are (2 4) and (−2 4). 64. (a) If = 2 + , then 0 = 2 + 1. If the point at which a tangent meets the parabola is 2 + , then the slope of the tangent is 2 + 1. But since it passes through (2 −3), the slope must also be ∆ ∆ = 2 + + 3 − 2 . Therefore, 2 + 1 = 2 + + 3 − 2 . Solving this equation for we get 2 + + 3 = 22 − 3 − 2 ⇔ 2 − 4 − 5 = ( − 5)( + 1) = 0 ⇔ = 5 or −1. If = −1, the point is (−1 0) and the slope is −1, so the equation is − 0 = (−1)( + 1) or = − − 1. If = 5, the point is (5 30) and the slope is 11, so the equation is − 30 = 11( − 5) or = 11 − 25. (b) As in part (a), but using the point (2 7), we get the equation 2 + 1 = 2 + − 7 − 2 ⇒ 22 − 3 − 2 = 2 + − 7 ⇔ 2 − 4 + 5 = 0. The last equation has no real solution (discriminant = −16 0), so there is no line through the point (2 7) that is tangent to the parabola. The diagram shows that the point (2 7) is “inside” the parabola, but tangent lines to the parabola do not pass through points inside the parabola. 65. 0() = lim →0 ( + ) − () = lim →0 1 + − 1 = lim →0 −((++)) = lim →0 (− + ) = lim →0 (−+1 ) = −12 66. (a) () = ⇒ 0() = −1 ⇒ 00() = ( − 1)−2 ⇒ · · · ⇒ ()() = ( − 1)( − 2) · · · 2 · 1− = ! (b) () = −1 ⇒ 0() = (−1)−2 ⇒ 00() = (−1)(−2)−3 ⇒ · · · ⇒ ()() = (−1)(−2)(−3) · · · (−)−(+1) = (−1)!−(+1) or (−1) ! +1 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.174 ¤ CHAPTER 3 DIFFERENTIATION RULES 67. Let () = 2 + + . Then 0() = 2 + and 00() = 2. 00(2) = 2 ⇒ 2 = 2 ⇒ = 1. 0(2) = 3 ⇒ 2(1)(2) + = 3 ⇒ 4 + = 3 ⇒ = −1. (2) = 5 ⇒ 1(2)2 + (−1)(2) + = 5 ⇒ 2 + = 5 ⇒ = 3. So () = 2 − + 3. 68. = 2 + + ⇒ 0 = 2 + ⇒ 00 = 2. We substitute these expressions into the equation 00 + 0 − 2 = 2 to get (2) + (2 + ) − 2(2 + + ) = 2 2 + 2 + − 22 − 2 − 2 = 2 (−2)2 + (2 − 2) + (2 + − 2) = (1)2 + (0) + (0) The coefficients of 2 on each side must be equal, so −2 = 1 ⇒ = − 1 2. Similarly, 2 − 2 = 0 ⇒ = = − 1 2 and 2 + − 2 = 0 ⇒ −1 − 1 2 − 2 = 0 ⇒ = − 3 4. 69. = () = 3 + 2 + + ⇒ 0() = 32 + 2 + . The point (−2 6) is on , so (−2) = 6 ⇒ −8 + 4 − 2 + = 6 (1). The point (2 0) is on , so (2) = 0 ⇒ 8 + 4 + 2 + = 0 (2). Since there are horizontal tangents at (−2 6) and (2 0), 0(±2) = 0. 0(−2) = 0 ⇒ 12 − 4 + = 0 (3) and 0(2) = 0 ⇒ 12 + 4 + = 0 (4). Subtracting equation (3) from (4) gives 8 = 0 ⇒ = 0. Adding (1) and (2) gives 8 + 2 = 6, so = 3 since = 0. From (3) we have = −12, so (2) becomes 8 + 4(0) + 2(−12) + 3 = 0 ⇒ 3 = 16 ⇒ = 3 16. Now = −12 = −12 16 3 = − 9 4 and the desired cubic function is = 16 3 3 − 9 4 + 3. 70. = 2 + + ⇒ 0() = 2 + . The parabola has slope 4 at = 1 and slope −8 at = −1, so 0(1) = 4 ⇒ 2 + = 4 (1) and 0(−1) = −8 ⇒ −2 + = −8 (2). Adding (1) and (2) gives us 2 = −4 ⇔ = −2. From (1), 2 − 2 = 4 ⇔ = 3. Thus, the equation of the parabola is = 32 − 2 + . Since it passes through the point (2 15), we have 15 = 3(2)2 − 2(2) + ⇒ = 7, so the equation is = 32 − 2 + 7. 71. () = 2+ 1 + 1 if if ≥ 1 1 Calculate the left- and right-hand derivatives as defined in Exercise 2.8.64: −0 (1) = lim →0− (1 + ) − (1) = lim →0− [(1 + )2 + 1] − (1 + 1) = lim →0− 2 + 2 = lim →0−( + 2) = 2 and +0 (1) = lim →0+ (1 + ) − (1) = lim →0+ [(1 + ) + 1] − (1 + 1) = lim →0+ = lim →0+ 1 = 1. Since the left and right limits are different, lim →0 (1 + ) − (1) does not exist, that is, 0(1) does not exist. Therefore, is not differentiable at 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.1 DERIVATIVES OF POLYNOMIALS AND EXPONENTIAL FUNCTIONS ¤ 175 72. () = 2 if ≤ 0 2 − 2 if 0 2 2 − if ≥ 2 Investigate the left- and right-hand derivatives at = 0 and = 2: −0 (0) = lim →0− (0 + ) − (0) = lim →0− 2 −2(0) = 2 and +0 (0) = lim →0+ (0 + ) − (0) = lim →0+ (2 − 2 ) − 2(0) = lim →0+(2 − ) = 2, so is differentiable at = 0. −0 (2) = lim →0− (2 + ) − (2) = lim →0− 2(2 + ) − (2 + )2 − (2 − 2) = lim →0− −2− 2 = lim →0−(−2 − ) = −2 and +0 (2) = lim →0+ (2 + ) − (2) = lim →0+ [2 − (2 + )] − (2 − 2) = lim →0+ − = lim →0+(−1) = −1, so is not differentiable at = 2. Thus, a formula for 0 is 0() = 2 if ≤ 0 2 − 2 if 0 2 −1 if 2 73. (a) Note that 2 − 9 0 for 2 9 ⇔ || 3 ⇔ −3 3. So () = 2 − 9 if ≤ −3 −2 + 9 if −3 3 2 − 9 if ≥ 3 ⇒ 0() = 2 if −3 −2 if −3 3 2 if 3 = −22 if if |||| 33 To show that 0(3) does not exist we investigate lim →0 (3 + ) − (3) by computing the left- and right-hand derivatives defined in Exercise 2.8.64. −0 (3) = lim →0− (3 + ) − (3) = lim →0− [−(3 + )2 + 9] − 0 = lim →0− (−6 − ) = −6 and +0 (3) = lim →0+ (3 + ) − (3) = lim →0+ (3 + )2 − 9 − 0 = lim →0+ 6 + 2 = lim →0+(6 + ) = 6. Since the left and right limits are different, lim →0 (3 + ) − (3) does not exist, that is, 0(3) does not exist. Similarly, 0(−3) does not exist. Therefore, is not differentiable at 3 or at −3. (b) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.176 ¤ CHAPTER 3 DIFFERENTIATION RULES 74. If ≥ 1, then () = | − 1| + | + 2| = − 1 + + 2 = 2 + 1. If −2 1, then () = −( − 1) + + 2 = 3. If ≤ −2, then () = −( − 1) − ( + 2) = −2 − 1. Therefore, () = −2 − 1 if ≤ −2 3 if −2 1 2 + 1 if ≥ 1 ⇒ 0() = −2 if −2 0 if −2 1 2 if 1 To see that 0(1) = lim →1 () − (1) − 1 does not exist, observe that lim →1− () − (1) − 1 = lim →1− 3 − 3 3 − 1 = 0 but lim →1+ () − (1) − 1 = lim →1+ 2 − 2 − 1 = 2. Similarly, 0(−2) does not exist. 75. Substituting = 1 and = 1 into = 2 + gives us + = 1 (1). The slope of the tangent line = 3 − 2 is 3 and the slope of the tangent to the parabola at ( ) is 0 = 2 + . At = 1, 0 = 3 ⇒ 3 = 2 + (2). Subtracting (1) from (2) gives us 2 = and it follows that = −1. The parabola has equation = 22 − . 76. = 4 + 3 + 2 + + ⇒ (0) = . Since the tangent line = 2 + 1 is equal to 1 at = 0, we must have = 1. 0 = 43 + 32 + 2 + ⇒ 0(0) = . Since the slope of the tangent line = 2 + 1 at = 0 is 2, we must have = 2. Now (1) = 1 + + + + = + + 4 and the tangent line = 2 − 3 at = 1 has -coordinate −1, so + + 4 = −1 or + = −5 (1). Also, 0(1) = 4 + 3 + 2 + = 3 + 2 + 6 and the slope of the tangent line = 2 − 3 at = 1 is −3, so 3 + 2 + 6 = −3 or 3 + 2 = −9 (2). Adding −2 times (1) to (2) gives us = 1 and hence, = −6. The curve has equation = 4 + 3 − 62 + 2 + 1. 77. = () = 2 ⇒ 0() = 2. So the slope of the tangent to the parabola at = 2 is = 2(2) = 4. The slope of the given line, 2 + = ⇔ = −2 + , is seen to be −2, so we must have 4 = −2 ⇔ = − 1 2. So when = 2, the point in question has -coordinate − 1 2 · 22 = −2. Now we simply require that the given line, whose equation is 2 + = , pass through the point (2 −2): 2(2) + (−2) = ⇔ = 2. So we must have = − 1 2 and = 2. 78. The slope of the curve = √ is 0 = 2 √ and the slope of the tangent line = 3 2 + 6 is 3 2. These must be equal at the point of tangency √ , so 2 √ = 3 2 ⇒ = 3 √. The -coordinates must be equal at = , so √ = 3 2 + 6 ⇒ 3 √ √ = 3 2 + 6 ⇒ 3 = 3 2 + 6 ⇒ 3 2 = 6 ⇒ = 4. Since = 3 √, we have = 3 √4 = 6. 79. The line = 2 + 3 has slope 2. The parabola = 2 ⇒ 0 = 2 has slope 2 at = . Equating slopes gives us 2 = 2, or = 1. Equating -coordinates at = gives us 2 = 2 + 3 ⇔ () = 2 + 3 ⇔ 1 = 2 + 3 ⇔ = −3. Thus, = 1 = − 1 3 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.1 DERIVATIVES OF POLYNOMIALS AND EXPONENTIAL FUNCTIONS ¤ 177 80. () = 2 + + ⇒ 0() = 2 + . The slope of the tangent line at = is 2 + , the slope of the tangent line at = is 2 + , and the average of those slopes is (2 + ) + (2 + ) 2 = + + . The midpoint of the interval [ ] is + 2 and the slope of the tangent line at the midpoint is 2 +2 + = ( + ) + . This is equal to + + , as required. 81. is clearly differentiable for 2 and for 2. For 2, 0() = 2, so −0 (2) = 4. For 2, 0() = , so +0 (2) = . For to be differentiable at = 2, we need 4 = −0 (2) = +0 (2) = . So () = 4 + . We must also have continuity at = 2, so 4 = (2) = lim →2+ () = lim →2+ (4 + ) = 8 + . Hence, = −4. 82. (a) = ⇒ = . Let = . The slope of the tangent line at = is 0() = −2 . Its equation is − = − 2 ( − ) or = − 2 + 2 , so its -intercept is 2 . Setting = 0 gives = 2, so the -intercept is 2. The midpoint of the line segment joining0 2and (2 0) is = . (b) We know the - and -intercepts of the tangent line from part (a), so the area of the triangle bounded by the axes and the tangent is 1 2(base)(height) = 1 2 = 1 2(2)(2) = 2, a constant. 83. Solution 1: Let () = 1000. Then, by the definition of a derivative, 0(1) = lim →1 () − (1) − 1 = lim →1 1000 − 1 − 1 . But this is just the limit we want to find, and we know (from the Power Rule) that 0() = 1000999, so 0(1) = 1000(1)999 = 1000. So lim →1 1000 − 1 − 1 = 1000. Solution 2: Note that (1000 − 1) = ( − 1)(999 + 998 + 997 + · · · + 2 + + 1). So lim →1 1000 − 1 − 1 = lim →1 ( − 1)(999 + 998 + 997 + · · · + 2 + + 1) − 1 = lim →1 (999 + 998 + 997 + · · · + 2 + + 1) = 1 + 1 + 1 + · · · + 1 + 1 + 1 = 1000, as above. 1000 ones 84. In order for the two tangents to intersect on the -axis, the points of tangency must be at equal distances from the -axis, since the parabola = 2 is symmetric about the -axis. Say the points of tangency are 2 and − 2, for some 0. Then since the derivative of = 2 is = 2, the left-hand tangent has slope −2 and equation − 2 = −2( + ), or = −2 − 2, and similarly the right-hand tangent line has equation − 2 = 2( − ), or = 2 − 2. So the two lines intersect at 0 −2. Now if the lines are perpendicular, then the product of their slopes is −1, so (−2)(2) = −1 ⇔ 2 = 1 4 ⇔ = 1 2. So the lines intersect at 0 − 1 4. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.178 ¤ CHAPTER 3 DIFFERENTIATION RULES 85. = 2 ⇒ 0 = 2, so the slope of a tangent line at the point ( 2) is 0 = 2 and the slope of a normal line is −1(2), for 6= 0. The slope of the normal line through the points ( 2) and (0 ) is 2 − − 0 , so 2 − = − 1 2 ⇒ 2 − = − 1 2 ⇒ 2 = − 1 2. The last equation has two solutions if 1 2, one solution if = 1 2, and no solution if 1 2. Since the -axis is normal to = 2 regardless of the value of (this is the case for = 0), we have three normal lines if 1 2 and one normal line if ≤ 1 2. 86. From the sketch, it appears that there may be a line that is tangent to both curves. The slope of the line through the points ( 2) and ( 2 − 2 + 2) is 2 − 2 + 2 − 2 − . The slope of the tangent line at is 2 [0 = 2] and at is 2 − 2 [0 = 2 − 2]. All three slopes are equal, so 2 = 2 − 2 ⇔ = − 1. Also, 2 − 2 = 2 − 2 + 2 − 2 − ⇒ 2 − 2 = 2 − 2−+ 2 (−−(1) − 1)2 ⇒ 2 − 2 = 2 − 2 + 2 − 2 + 2 − 1 ⇒ 2 = 3 ⇒ = 3 2 and = 3 2 − 1 = 1 2. Thus, an equation of the tangent line at is − 1 22 = 2 1 2 − 1 2 or = − 1 4. APPLIED PROJECT Building a Better Roller Coaster 1. (a) () = 2 + + ⇒ 0() = 2 + . The origin is at : (0) = 0 ⇒ = 0 The slope of the ascent is 08: 0(0) = 08 ⇒ = 08 The slope of the drop is −16: 0(100) = −16 ⇒ 200 + = −16 (b) = 08, so 200 + = −16 ⇒ 200 + 08 = −16 ⇒ 200 = −24 ⇒ = − 24 200 = −0012. Thus, () = −00122 + 08. (c) Since 1 passes through the origin with slope 08, it has equation = 08. The horizontal distance between and is 100, so the -coordinate at is (100) = −0012(100)2 + 08(100) = −40. Since 2 passes through the point (100 −40) and has slope −16, it has equation + 40 = −16( − 100) or = −16 + 120. (d) The difference in elevation between (0 0) and (100 −40) is 0 − (−40) = 40 feet. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.APPLIED PROJECT BUILDING A BETTER ROLLER COASTER ¤ 179 2. (a) Interval Function First Derivative Second Derivative (−∞ 0) 1() = 08 0 1() = 08 00 1() = 0 [0 10) () = 3 + 2 + + 0() = 32 + 2 + 00() = 6 + 2 [10 90] () = 2 + + 0() = 2 + 00() = 2 (90 100] () = 3 + 2 + + 0() = 32 + 2 + 00() = 6 + 2 (100 ∞) 2() = −16 + 120 0 2() = −16 00 2() = 0 There are 4 values of (0, 10, 90, and 100) for which we must make sure the function values are equal, the first derivative values are equal, and the second derivative values are equal. The third column in the following table contains the value of each side of the condition— these are found after solving the system in part (b). At = Condition Value Resulting Equation 0 (0) = 1(0) 0 = 0 0(0) = 0 1(0) 4 5 = 08 00(0) = 00 1(0) 0 2 = 0 10 (10) = (10) 68 9 1000 + 100 + 10 + = 100 + 10 + 0(10) = 0(10) 2 3 300 + 20 + = 20 + 00(10) = 00(10) − 75 2 60 + 2 = 2 90 (90) = (90) − 220 9 729,000 + 8100 + 90 + = 8100 + 90 + 0(90) = 0(90) − 22 15 24,300 + 180 + = 180 + 00(90) = 00(90) − 75 2 540 + 2 = 2 100 (100) = 2(100) −40 1,000,000 + 10,000 + 100 + = −40 0(100) = 0 2(100) − 8 5 30,000 + 200 + = −16 00(100) = 00 2(100) 0 600 + 2 = 0 (b) We can arrange our work in a 12 × 12 matrix as follows. constant 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 08 0 0 0 0 2 0 0 0 0 0 0 0 −100 −10 −1 1000 100 10 1 0 0 0 0 0 −20 −1 0 300 20 1 0 0 0 0 0 0 −2 0 0 60 2 0 0 0 0 0 0 0 −8100 −90 −1 0 0 0 0 729,000 8100 90 1 0 −180 −1 0 0 0 0 0 24,300 180 1 0 0 −2 0 0 0 0 0 0 540 2 0 0 0 0 0 0 0 0 0 0 1,000,000 10,000 100 1 −40 0 0 0 0 0 0 0 30,000 200 1 0 −16 0 0 0 0 0 0 0 600 2 0 0 0 Solving the system gives us the formulas for , , and . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.180 ¤ CHAPTER 3 DIFFERENTIATION RULES = −0013 = − 1 75 = 093 = 14 15 = −04 = − 4 9 () = − 75 1 2 + 14 15 − 4 9 = −00004 = − 1 2250 = 0 = 08 = 4 5 = 0 () = − 2250 1 3 + 4 5 = 00004 = 2250 1 = −013 = − 15 2 = 1173 = 176 15 = −3244 = − 2920 9 () = 2250 1 3 − 15 2 2 + 176 15 − 2920 9 (c) Graph of 1, , , , and 2: The graph of the five functions as a piecewise-defined function: This is the piecewise-defined function assignment on a TI-83/4 Plus calculator, where Y2 = 1, Y6 = , Y5 = , Y7 = , and Y3 = 2. A comparison of the graphs in part 1(c) and part 2(c): 3.2 The Product and Quotient Rules 1. Product Rule: () = (1 + 22)( − 2) ⇒ 0() = (1 + 22)(1 − 2) + ( − 2)(4) = 1 − 2 + 22 − 43 + 42 − 43 = 1 − 2 + 62 − 83. Multiplying first: () = (1 + 22)( − 2) = − 2 + 23 − 24 ⇒ 0() = 1 − 2 + 62 − 83 (equivalent). 2. Quotient Rule: () = 4 − 53 + √ 2 = 4 − 53 + 12 2 ⇒ 0() = 2(43 − 152 + 1 2−12) − (4 − 53 + 12)(2) (2)2 = 45 − 154 + 1 232 − 25 + 104 − 232 4 = 25 − 54 − 3 232 4 = 2 − 5 − 3 2−52 Simplifying first: () = 4 − 53 + √ 2 = 2 − 5 + −32 ⇒ 0() = 2 − 5 − 3 2−52 (equivalent). For this problem, simplifying first seems to be the better method. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.2 THE PRODUCT AND QUOTIENT RULES ¤ 181 3. By the Product Rule, () = (32 − 5) ⇒ 0() = (32 − 5)()0 + (32 − 5)0 = (32 − 5) + (6 − 5) = [(32 − 5) + (6 − 5)] = (32 + − 5) 4. By the Product Rule, () = ( + 2√ ) ⇒ 0() = ( + 2√ )()0 + ( + 2√ )0 = ( + 2√ ) + 1 + 2 · 1 2−12 = ( + 2√ ) + 1 + 1√ = + 2√ + 1 + 1√ 5. By the Quotient Rule, = ⇒ 0 = (1) − () ()2 = (1 − ) ()2 = 1 − . 6. By the Quotient Rule, = 1 − ⇒ 0 = (1 − ) − (−) (1 − )2 = − 2 + 2 (1 − )2 = (1 − )2 . The notations PR ⇒ and QR ⇒ indicate the use of the Product and Quotient Rules, respectively. 7. () = 1 + 2 3 − 4 QR ⇒ 0() = (3 − 4)(2) − (1 + 2)(−4) (3 − 4)2 = 6 − 8 + 4 + 8 (3 − 4)2 = 10 (3 − 4)2 8. () = 2 − 2 2 + 1 QR ⇒ 0() = (2 + 1)(2) − (2 − 2)(2) (2 + 1)2 = 42 + 2 − 22 + 4 (2 + 1)2 = 22 + 2 + 4 (2 + 1)2 9. () = ( − √ )( + √ ) ⇒PR 0() = ( − √ ) 1 + 2√1 + ( + √ ) 1 − 2√1 = + 1 2√ − √ − 1 2 + − 1 2√ + √ − 1 2 = 2 − 1. An easier method is to simplify first and then differentiate as follows: () = ( − √ )( + √ ) = 2 − (√ )2 = 2 − ⇒ 0() = 2 − 1 10. () = (3 − 2)(−4 + −2) ⇒PR 0() = (3 − 2)(−4−5 − 2−3) + (−4 + −2)(32 − 2) = −4−2 − 20 + 8−4 + 4−2 + 3−2 − 2−4 + 30 − 2−2 = 1 + −2 + 6−4 11. () = 12 − 34 ( + 53) = (−2 − 3−4)( + 53) ⇒PR 0() = (−2 − 3−4)(1 + 152) + ( + 53)(−2−3 + 12−5) = (−2 + 15 − 3−4 − 45−2) + (−2−2 + 12−4 − 10 + 60−2) = 5 + 14−2 + 9−4 or 5 + 142 + 94 12. () = (1 − )( + ) ⇒PR 0() = (1 − )(1 + ) + ( + )(−) = 12 − ()2 − − ()2 = 1 − − 22 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.182 ¤ CHAPTER 3 DIFFERENTIATION RULES 13. = 2 + 1 3 − 1 QR ⇒ 0 = (3 − 1)(2) − (2 + 1)(32) (3 − 1)2 = (3 − 1)(2) − (2 + 1)(3) (3 − 1)2 = (23 − 2 − 33 − 3) (3 − 1)2 = (−3 − 3 − 2) (3 − 1)2 14. = √ 2 + QR ⇒ 0 = (2 + )2√1 − √ (1) (2 + )2 = 1 √ + √ 2 − √ (2 + )2 = 2 + − 2 2√ (2 + )2 = 2 − 2√(2 + )2 15. = 3 + 3 2 − 4 + 3 QR ⇒ 0 = (2 − 4 + 3)(32 + 3) − (3 + 3)(2 − 4) (2 − 4 + 3)2 = 34 + 32 − 123 − 12 + 92 + 9 − (24 − 43 + 62 − 12) (2 − 4 + 3)2 = 4 − 83 + 62 + 9 (2 − 4 + 3)2 16. = 1 3 + 22 − 1 QR ⇒ 0 = (3 + 22 − 1)(0) − 1(32 + 4) (3 + 22 − 1)2 = − 32 + 4 (3 + 22 − 1)2 17. = ( + √ ) = ( + 32) ⇒PR 0 = 1 + 3 212 + ( + 32) = 1 + 3 2√ + + √ 18. () = + QR ⇒ 0() = ( + )() − ()() ( + )2 = + 2 − 2 ( + )2 = ( + )2 19. = − √ 2 = 2 − √ 2 = −1 − −32 ⇒ 0 = −−2 + 3 2−52 = −21 + 2352 = 32−52√2 20. = (2 + )√ ⇒PR 0 = (2 + )2√1 + √ (2 + ) = 2√2 + 2√ + 2√ + √ = 2 + + 42 + 2 2√ = 52 + + 2 2√ 21. () = √3 − 3 QR ⇒ 0() = ( − 3) 1 3−23 − 13(1) ( − 3)2 = 13 13 − −23 − 13 ( − 3)2 = − 23 13 − −23 ( − 3)2 = −2 323 − 3 323 ( − 3)2 = −2 − 3 323( − 3)2 22. () = 4 + QR ⇒ 0() = (1) − (4 + )( + (1)) ()2 = − 4 − 4 − 2 − 22 = −4 − 4 − 2 22 = −(2 + 4 + 4) 22 = − ( + 2)2 2 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.2 THE PRODUCT AND QUOTIENT RULES ¤ 183 23. () = 2 2 + QR ⇒ 0() = (2 + ) 2 + (2) − 2(2 + ) (2 + )2 = 4 + 23 + 22 + 22 − 23 − 22 (2 + )2 = 4 + 22 (2 + )2 = (3 + 2) (2 + )2 24. () = 2 + 3 = + 2 QR ⇒ 0() = ( + 2)(0) − ( + 2) ( + 2)2 = −( + 2) ()2( + )2 = − ( + 2) 2( + )2 25. () = + ⇒ 0() = ( + )(1) +−(1 2 − 2) = + 2−+ +2 = (2 2 +2 )2 · 2 2 = (22+)2 26. () = + + ⇒ 0() = ( + )( ( ) +− ( )2 + )() = +( +− )2 − = ( +−)2 27. () = (3 + 1) ⇒PR 0() = (3 + 1) + (32) = (3 + 1) + 32 = (3 + 32 + 1) ⇒PR 00() = (32 + 6) + (3 + 32 + 1) = (32 + 6) + (3 + 32 + 1) = (3 + 62 + 6 + 1) 28. () = √ ⇒PR 0() = √ + 2√1 = √ + 2√1 = 22√+ 1 . Using the Product Rule and 0() = 12 + 1 2−12, we get 00() = 12 + 1 2−12 + 1 2−12 − 1 4−32 = 12 + −12 − 1 4−32 = 424+ 4 32− 1 29. () = 2 1 + QR ⇒ 0() = (1 + )(2) − 2() (1 + )2 = [(1 + )2 − ] (1 + )2 = (2 + 2 − ) (1 + )2 . Using the Quotient and Product Rules and 0() = 2 + 2 − 2 (1 + )2 , we get 00() = (1 + )2 2 + 2( + ) − (2 + 2) − (2 + 2 − 2) [(1 + ) + (1 + )] [(1 + )2]2 = (1 + ) (1 + )(2 + 2 + 2 − 2 − 2) − (2 + 2 − 2)(2) (1 + )4 = (1 + )(2 + 2 − 2) − 4 − 42 + 222 (1 + )3 = 2 + 2 − 2 + 2 + 22 − 22 − 4 − 42 + 222 (1 + )3 = 2 + 4 − 2 − 4 + 22 + 22 − 42 (1 + )3 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.184 ¤ CHAPTER 3 DIFFERENTIATION RULES 30. () = 2 − 1 ⇒ 0() = (2 −(1)(1) 2 − 1) −2(2) = 2(−21−−1)222 = (−22−−1)12 ⇒ 00() = (2 − 1)2(−2) − (−2 − 1)(4 − 22 + 1)0 [(2 − 1)2]2 = (2 − 1)2(−2) + (2 + 1)(43 − 4) (2 − 1)4 = (2 − 1)2(−2) + (2 + 1)(4)(2 − 1) (2 − 1)4 = (2 − 1)[(2 − 1)(−2) + (2 + 1)(4)] (2 − 1)4 = −23 + 2 + 43 + 4 (2 − 1)3 = 23 + 6 (2 − 1)3 31. = 2 − 1 2 + + 1 ⇒ 0 = (2 + + 1)(2) − (2 − 1)(2 + 1) (2 + + 1)2 = 23 + 22 + 2 − 23 − 2 + 2 + 1 (2 + + 1)2 = 2 + 4 + 1 (2 + + 1)2 . At (1 0), 0 = 6 32 = 2 3 , and an equation of the tangent line is − 0 = 2 3( − 1), or = 2 3 − 2 3. 32. = 1 + 1 + ⇒ 0 = (1 + )(1) − (1 + ) (1 + )2 = 1 + − − (1 + )2 = 1 − (1 + )2 . At 0 1 2, 0 = 1 (1 + 1)2 = 1 4 , and an equation of the tangent line is − 1 2 = 1 4( − 0) or = 1 4 + 1 2. 33. = 2 ⇒ 0 = 2( · + · 1) = 2( + 1). At (0 0), 0 = 20(0 + 1) = 2 · 1 · 1 = 2, and an equation of the tangent line is − 0 = 2( − 0), or = 2. The slope of the normal line is − 1 2, so an equation of the normal line is − 0 = − 1 2( − 0), or = − 1 2. 34. = 2 2 + 1 ⇒ 0 = (2 + 1)(2) (2 + 1) − 22(2) = (22−+ 1) 222 . At (1 1), 0 = 0, and an equation of the tangent line is − 1 = 0( − 1), or = 1. The slope of the normal line is undefined, so an equation of the normal line is = 1. 35. (a) = () = 1 1 + 2 ⇒ 0() = (1 + 2)(0) − 1(2) (1 + 2)2 = −2 (1 + 2)2 . So the slope of the tangent line at the point −1 1 2 is 0(−1) = 222 = 1 2 and its equation is − 1 2 = 1 2( + 1) or = 1 2 + 1. (b) 36. (a) = () = 1 + 2 ⇒ 0() = (1 + 2)1 − (2) (1 + 2)2 = 1 − 2 (1 + 2)2 . So the slope of the tangent line at the point (3 03) is 0(3) = 100 −8 and its equation is − 03 = −008( − 3) or = −008 + 054. (b) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.2 THE PRODUCT AND QUOTIENT RULES ¤ 185 37. (a) () = (3 − ) ⇒ 0() = (3 − ) + (32 − 1) = (3 + 32 − − 1) (b) 0 = 0 when has a horizontal tangent line, 0 is negative when is decreasing, and 0 is positive when is increasing. 38. (a) () = 22 + + 1 ⇒ 0() = (22 + + 1) − (4 + 1) (22 + + 1)2 = (22 + + 1 − 4 − 1) (22 + + 1)2 = (22 − 3) (22 + + 1)2 (b) 0 = 0 when has a horizontal tangent line, 0 is negative when is decreasing, and 0 is positive when is increasing. 39. (a) () = 2 − 1 2 + 1 ⇒ 0() = (2 + 1)(2) − (2 − 1)(2) (2 + 1)2 = (2)[(2 + 1) − (2 − 1)] (2 + 1)2 = (2)(2) (2 + 1)2 = 4 (2 + 1)2 ⇒ 00() = (2 + 1)2(4) − 4(4 + 22 + 1)0 [(2 + 1)2]2 = 4(2 + 1)2 − 4(43 + 4) (2 + 1)4 = 4(2 + 1)2 − 162(2 + 1) (2 + 1)4 = 4(2 + 1)[(2 + 1) − 42] (2 + 1)4 = 4(1 − 32) (2 + 1)3 (b) 0 = 0 when has a horizontal tangent and 00 = 0 when 0 has a horizontal tangent. 0 is negative when is decreasing and positive when is increasing. 00 is negative when 0 is decreasing and positive when 0 is increasing. 00 is negative when is concave down and positive when is concave up. 40. (a) () = (2 − 1) ⇒ 0() = (2 − 1) + (2) = (2 + 2 − 1) ⇒ 00() = (2 + 2) + (2 + 2 − 1) = (2 + 4 + 1) (b) We can see that our answers are plausible, since has horizontal tangents where 0() = 0, and 0 has horizontal tangents where 00() = 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.186 ¤ CHAPTER 3 DIFFERENTIATION RULES 41. () = 2 1 + ⇒ 0() = (1 + )(2) − 2(1) (1 + )2 = 2 + 22 − 2 (1 + )2 = 2 + 2 2 + 2 + 1 ⇒ 00() = (2 + 2 + 1)(2 + 2) − (2 + 2)(2 + 2) (2 + 2 + 1)2 = (2 + 2)(2 + 2 + 1 − 2 − 2) [( + 1)2]2 = 2( + 1)(1) ( + 1)4 = 2 ( + 1)3 , so 00(1) = 2 (1 + 1)3 = 2 8 = 1 4 . 42. () = ⇒ 0() = · 1 − · ()2 = (1 − ) ()2 = 1 − ⇒ 00() = · (−1) − (1 − ) ()2 = [−1 − (1 − )] ()2 = − 2 ⇒ 000() = · 1 − ( − 2) ()2 = [1 − ( − 2)] ()2 = 3 − ⇒ (4)() = · (−1) − (3 − ) ()2 = [−1 − (3 − )] ()2 = − 4 . The pattern suggests that ()() = ( − )(−1) . (We could use mathematical induction to prove this formula.) 43. We are given that (5) = 1, 0(5) = 6, (5) = −3, and 0(5) = 2. (a) ()0(5) = (5)0(5) + (5) 0(5) = (1)(2) + (−3)(6) = 2 − 18 = −16 (b) 0 (5) = (5) 0(5) [(5)] − 2(5)0(5) = (−3)(6) (−3) −2(1)(2) = −20 9 (c) 0 (5) = (5)0(5) [(5)] − 2(5) 0(5) = (1)(2)(1) − (2−3)(6) = 20 44. We are given that (4) = 2, (4) = 5, 0(4) = 6, and 0(4) = −3. (a) () = 3() + 8() ⇒ 0() = 3 0() + 80(), so 0(4) = 3 0(4) + 80(4) = 3(6) + 8(−3) = 18 − 24 = −6. (b) () = () () ⇒ 0() = () 0() + () 0(), so 0(4) = (4) 0(4) + (4) 0(4) = 2(−3) + 5(6) = −6 + 30 = 24. (c) () = () () ⇒ 0() = () 0([)(−)] 2() 0(), so 0(4) = (4) 0(4) − (4) 0(4) [(4)]2 = 5(6) − 2(−3) 52 = 30 + 6 25 = 36 25 . (d) () = () () + () ⇒ 0(4) = [(4) + (4)] 0(4) − (4) [ 0(4) + 0(4)] [(4) + (4)]2 = (2 + 5) (−3) − 5 [6 + (−3)] (2 + 5)2 = −21 − 15 72 = − 36 49 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.2 THE PRODUCT AND QUOTIENT RULES ¤ 187 45. () = () ⇒ 0() = 0() + () = [0() + ()]. 0(0) = 0[0(0) + (0)] = 1(5 + 2) = 7 46. () = 0() −2() · 1 ⇒ ()=2 = 20(2)2−2 (2) = 2(−3)4− (4) = −410 = −25 47. () = () ⇒ 0() = 0() + () · 1. Now (3) = 3(3) = 3 · 4 = 12 and 0(3) = 3 0(3) + (3) = 3(−2) + 4 = −2. Thus, an equation of the tangent line to the graph of at the point where = 3 is − 12 = −2( − 3), or = −2 + 18. 48. 0() = 2() ⇒ 00() = 2 0() + () · 2. Now 0(2) = 22(2) = 4(10) = 40, so 00(2) = 22(40) + 10(4) = 200. 49. (a) From the graphs of and , we obtain the following values: (1) = 2 since the point (1 2) is on the graph of ; (1) = 1 since the point (1 1) is on the graph of ; 0(1) = 2 since the slope of the line segment between (0 0) and (2 4) is 4 − 0 2 − 0 = 2; 0(1) = −1 since the slope of the line segment between (−2 4) and (2 0) is 0 − 4 2 − (−2) = −1. Now () = ()(), so 0(1) = (1)0(1) + (1) 0(1) = 2 · (−1) + 1 · 2 = 0. (b) () = ()(), so 0(5) = (5) 0(5) − (5)0(5) [(5)]2 = 2− 1 3 − 3 · 2 3 22 = − 83 4 = − 2 3 50. (a) () = () (), so 0(2) = (2) 0(2) + (2) 0(2) = 3 · 2 4 + 2 · 0 = 3 2 (b) () = ()(), so 0(7) = (7) 0(7) − (7) 0(7) [(7)]2 = 1 · 1 4 − 5 · − 2 3 12 = 1 4 + 10 3 = 43 12 51. (a) = () ⇒ 0 = 0() + () · 1 = 0() + () (b) = () ⇒ 0 = () · [1(−)] 2 0() = ()[−( )]20() (c) = () ⇒ 0 = 0() − () · 1 ()2 = 0() − () 2 52. (a) = 2() ⇒ 0 = 2 0() + ()(2) (b) = () 2 ⇒ 0 = 2 0()(−2)2()(2) = 0()−3 2() (c) = 2 () ⇒ 0 = ()(2[)(−)]22 0() (d) = 1 +√ () ⇒ 0 = √ [ 0() + ()] − [1 + ()] 1 2 √ (√ )2 = 32 0() + 12() − 1 2−12 − 1 212() · 212 212 = () + 22 0() − 1 232 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.188 ¤ CHAPTER 3 DIFFERENTIATION RULES 53. If = () = + 1 , then 0() = ( + 1)(1) − (1) ( + 1)2 = 1 ( + 1)2 . When = , the equation of the tangent line is − + 1 = 1 ( + 1)2 ( − ). This line passes through (1 2) when 2 − + 1 = ( + 1) 1 2 (1 − ) ⇔ 2( + 1)2 − ( + 1) = 1 − ⇔ 22 + 4 + 2 − 2 − − 1 + = 0 ⇔ 2 + 4 + 1 = 0. The quadratic formula gives the roots of this equation as = −4 ± 42 − 4(1)(1) 2(1) = −4 ± √12 2 = −2 ± √3, so there are two such tangent lines. Since −2 ± √3 = −2 ± √3 −2 ± √3 + 1 = −2 ± √3 −1 ± √3 · −1 ∓ √3 −1 ∓ √3 = 2 ± 2 √3 ∓ √3 − 3 1 − 3 = −1 ± √3 −2 = 1 ∓ √3 2 , the lines touch the curve at −2 + √3 1 −2√3 ≈ (−027 −037) and −2 − √3 1 +2√3 ≈ (−373 137). 54. = − 1 + 1 ⇒ 0 = ( + 1)(1) − ( − 1)(1) ( + 1)2 = 2 ( + 1)2 . If the tangent intersects the curve when = , then its slope is 2( + 1)2. But if the tangent is parallel to − 2 = 2, that is, = 1 2 − 1, then its slope is 1 2. Thus, 2 ( + 1)2 = 1 2 ⇒ ( + 1)2 = 4 ⇒ + 1 = ±2 ⇒ = 1 or −3. When = 1, = 0 and the equation of the tangent is − 0 = 1 2( − 1) or = 1 2 − 1 2. When = −3, = 2 and the equation of the tangent is − 2 = 1 2( + 3) or = 1 2 + 7 2. 55. = ⇒ 0 = 0 − 0 2 . For () = − 33 + 55, 0() = 1 − 92 + 254, and for () = 1 + 33 + 66 + 99, 0() = 92 + 365 + 818. Thus, 0(0) = (0) 0(0) − (0)0(0) [(0)]2 = 1 · 1 − 0 · 0 12 = 1 1 = 1. 56. = ⇒ 0 = 0 − 0 2 . For () = 1 + + 2 + , 0() = 1 + 2 + + , and for () = 1 − + 2 − , 0() = −1 + 2 − − . Thus, 0(0) = (0) 0(0) − (0)0(0) [(0)]2 = 1 · 2 − 1 · (−2) 12 = 4 1 = 4. 57. If () denotes the population at time and () the average annual income, then () = ()() is the total personal income. The rate at which () is rising is given by 0() = ()0() + () 0() ⇒ 0(1999) = (1999)0(1999) + (1999) 0(1999) = (961,400)($1400yr) + ($30,593)(9200yr) = $1,345,960,000yr + $281,455,600yr = $1,627,415,600yr So the total personal income was rising by about $1.627 billion per year in 1999. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.2 THE PRODUCT AND QUOTIENT RULES ¤ 189 The term ()0() ≈ $1.346 billion represents the portion of the rate of change of total income due to the existing population’s increasing income. The term () 0() ≈ $281 million represents the portion of the rate of change of total income due to increasing population. 58. (a) (20) = 10,000 means that when the price of the fabric is $20yard, 10,000 yards will be sold. 0(20) = −350 means that as the price of the fabric increases past $20yard, the amount of fabric which will be sold is decreasing at a rate of 350 yards per (dollar per yard). (b) () = () ⇒ 0() = 0() + () · 1 ⇒ 0(20) = 20 0(20) + (20) · 1 = 20(−350) + 10,000 = 3000. This means that as the price of the fabric increases past $20yard, the total revenue is increasing at $3000($yard). Note that the Product Rule indicates that we will lose $7000($yard) due to selling less fabric, but this loss is more than made up for by the additional revenue due to the increase in price. 59. = 014[S] 0015 + [S] ⇒ [S] = (0015 + [S])(014) − (014[S])(1) (0015 + [S])2 = 00021 (0015 + [S])2 . [S] represents the rate of change of the rate of an enzymatic reaction with respect to the concentration of a substrate S. 60. () = () () ⇒ 0() = () 0() + () 0(), so 0(4) = (4) 0(4) + (4) 0(4) = 820(014) + 12(50) = 1748 gweek. 61. (a) ()0 = [()]0 = ()0 + ()0 = ( 0 + 0) + ()0 = 0 + 0 + 0 (b) Putting = = in part (a), we have [()]3 = ()0 = 0 + 0 + 0 = 3 0 = 3[()]2 0(). (c) (3) = ()3 = 3()2 = 32 = 33 62. (a) We use the Product Rule repeatedly: = ⇒ 0 = 0 + 0 ⇒ 00 = ( 00 + 00) + ( 00 + 00) = 00 + 2 00 + 00. (b) 000 = 000 + 000 + 2 ( 000 + 000) + 000 + 000 = 000 + 3 000 + 3 000 + 000 ⇒ (4) = (4) + 0000 + 3 ( 0000 + 0000) + 3 ( 0000 + 0000) + 0000 + (4) = (4) + 4 0000 + 6 0000 + 4 0000 + (4) (c) By analogy with the Binomial Theorem, we make the guess: () = () + (−1)0 + 2 (−2)00 + · · · + (−)() + · · · + 0(−1) + (), where = ! (−! )! = ( − 1)( − 2) !· · · ( − + 1). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.190 ¤ CHAPTER 3 DIFFERENTIATION RULES 63. For () = 2, 0() = 2 + (2) = (2 + 2). Similarly, we have 00() = (2 + 4 + 2) 000() = (2 + 6 + 6) (4)() = (2 + 8 + 12) (5)() = (2 + 10 + 20) It appears that the coefficient of in the quadratic term increases by 2 with each differentiation. The pattern for the constant terms seems to be 0 = 1 · 0, 2 = 2 · 1, 6 = 3 · 2, 12 = 4 · 3, 20 = 5 · 4. So a reasonable guess is that ()() = [2 + 2 + ( − 1)]. Proof: Let be the statement that ()() = [2 + 2 + ( − 1)]. 1. 1 is true because 0() = (2 + 2). 2. Assume that is true; that is, ()() = [2 + 2 + ( − 1)]. Then (+1)() = ()() = (2 + 2) + [2 + 2 + ( − 1)] = [2 + (2 + 2) + (2 + )] = [2 + 2( + 1) + ( + 1)] This shows that +1 is true. 3. Therefore, by mathematical induction, is true for all ; that is, ()() = [2 + 2 + ( − 1)] for every positive integer . 64. (a) (1) = () · (1) [(−)]12· [()] [Quotient Rule] = () ·[0(−)] 12· 0() = 0[−(0)] (2 ) = −[(0()] )2 (b) 3 + 212 − 1 = −(33 + 2 + 222 −−1) 120 = −(3 + 2 32 + 4 2 −1)2 (c) (−) = 1 = −(())20 [by the Reciprocal Rule] = −2−1 = −−1−2 = −−−1 3.3 Derivatives of Trigonometric Functions 1. () = 2 sin ⇒PR 0() = 2 cos + (sin )(2) = 2 cos + 2 sin 2. () = cos + 2 tan ⇒ 0() = (− sin ) + (cos )(1) + 2 sec2 = cos − sin + 2 sec2 3. () = cos ⇒ 0() = (− sin ) + (cos ) = (cos − sin ) 4. = 2 sec − csc ⇒ 0 = 2(sec tan ) − (− csc cot ) = 2 sec tan + csc cot 5. = sec tan ⇒ 0 = sec (sec2 ) + tan (sec tan ) = sec (sec2 + tan2 ). Using the identity 1 + tan2 = sec2 , we can write alternative forms of the answer as sec (1 + 2 tan2 ) or sec (2 sec2 − 1). 6. () = (tan − ) ⇒ 0() = (sec2 − 1) + (tan − ) = (sec2 − 1 + tan − ) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.3 DERIVATIVES OF TRIGONOMETRIC FUNCTIONS ¤ 191 7. = cos + 2 sin ⇒ 0 = (− sin ) + 2(cos ) + sin (2) = − sin + ( cos + 2 sin ) 8. () = cot ⇒ 0() = (− csc2())−2 (cot ) = (− csc (2)2− cot ) = −csc2 + cot 9. = 2 − tan ⇒ 0 = (2 − tan )(1) − (− sec2 ) (2 − tan )2 = 2 − tan + sec2 (2 − tan )2 10. = sin cos ⇒ 0 = sin (− sin ) + cos (cos ) = cos2 − sin2 [or cos 2] 11. () = sin 1 + cos ⇒ 0() = (1 + cos ) cos − (sin )(− sin ) (1 + cos )2 = cos + cos2 + sin2 (1 + cos )2 = cos + 1 (1 + cos )2 = 1 1 + cos 12. = cos 1 − sin ⇒ 0 = (1 − sin )(− sin ) − cos (− cos ) (1 − sin )2 = − sin + sin2 + cos2 (1 − sin )2 = − sin + 1 (1 − sin )2 = 1 1 − sin 13. = sin 1 + ⇒ 0 = (1 + )( cos + sin ) − sin(1) (1 + )2 = cos + sin + 2 cos + sin − sin (1 + )2 = (2 + ) cos + sin (1 + )2 14. = sin 1 + tan ⇒ 0 = (1 + tan ) cos − (sin ) sec2 (1 + tan )2 = cos + sin − sin cos2 (1 + tan )2 = cos + sin − tan sec (1 + tan )2 15. Using Exercise 3.2.61(a) , () = cos sin ⇒ 0() = 1 cos sin + (− sin ) sin + cos (cos ) = cos sin − sin2 + cos2 = sin cos + (cos2 − sin2 ) = 1 2 sin 2 + cos 2 [using double-angle formulas] 16. Using Exercise 3.2.61(a), () = cot ⇒ 0() = 1 cot + cot + (− csc2 ) = (cot + cot − csc2 ) 17. (csc ) = sin1 = (sin )(0) sin−2 1(cos ) = −sin cos 2 = −sin1 · cos sin = − csc cot 18. (sec ) = cos 1 = (cos )(0) cos −21( − sin ) = cos sin2 = cos 1 · cos sin = sec tan 19. (cot ) = cos sin = (sin )(− sin sin ) −2 (cos )(cos ) = −sin2 sin+ cos 2 2 = −sin12 = − csc2 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.192 ¤ CHAPTER 3 DIFFERENTIATION RULES 20. () = cos ⇒ 0() = lim →0 ( + ) − () = lim →0 cos ( + ) − cos = lim →0 cos cos − sin sin − cos = lim →0 cos cos − 1 − sin sin = cos lim →0 cos − 1 − sin lim →0 sin = (cos )(0) − (sin )(1) = − sin 21. = sin + cos ⇒ 0 = cos − sin , so 0(0) = cos 0 − sin 0 = 1 − 0 = 1. An equation of the tangent line to the curve = sin + cos at the point (0 1) is − 1 = 1( − 0) or = + 1. 22. = cos ⇒ 0 = (− sin ) + (cos ) = (cos − sin ) ⇒ the slope of the tangent line at (0 1) is 0(cos 0 − sin 0) = 1(1 − 0) = 1 and an equation is − 1 = 1( − 0) or = + 1. 23. = cos − sin ⇒ 0 = − sin − cos , so 0() = − sin − cos = 0 − (−1) = 1. An equation of the tangent line to the curve = cos − sin at the point ( −1) is − (−1) = 1( − ) or = − − 1. 24. = + tan ⇒ 0 = 1 + sec2 , so 0() = 1 + (−1)2 = 2. An equation of the tangent line to the curve = + tan at the point ( ) is − = 2( − ) or = 2 − . 25. (a) = 2 sin ⇒ 0 = 2( cos + sin · 1). At 2 , 0 = 2 2 cos 2 + sin 2 = 2(0 + 1) = 2, and an equation of the tangent line is − = 2 − 2 , or = 2. (b) 26. (a) = 3 + 6 cos ⇒ 0 = 3 − 6 sin . At 3 + 3, 0 = 3 − 6 sin 3 = 3 − 6 √23 = 3 − 3 √3, and an equation of the tangent line is − ( + 3) = 3 − 3 √3 − 3 , or = 3 − 3 √3 + 3 + √3. (b) 27. (a) () = sec − ⇒ 0() = sec tan − 1 (b) Note that 0 = 0 where has a minimum. Also note that 0 is negative when is decreasing and 0 is positive when is increasing. 28. (a) () = cos ⇒ 0() = (− sin ) + (cos ) = (cos − sin ) ⇒ 00() = (− sin − cos ) + (cos − sin ) = (− sin − cos + cos − sin ) = −2 sin °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.3 DERIVATIVES OF TRIGONOMETRIC FUNCTIONS ¤ 193 (b) Note that 0 = 0 where has a minimum and 00 = 0 where 0 has a minimum. Also note that 0 is negative when is decreasing and 00 is negative when 0 is decreasing. 29. () = sin ⇒ 0() = (cos ) + (sin ) · 1 = cos + sin ⇒ 00() = (− sin ) + (cos ) · 1 + cos = − sin + 2 cos 30. () = sec ⇒ 0() = sec tan ⇒ 00() = (sec ) sec2 + (tan ) sec tan = sec3 + sec tan2 , so 00 4 = √2 3 + √2(1)2 = 2√2 + √2 = 3√2. 31. (a) () = tan − 1 sec ⇒ 0() = sec (sec2 ) − (tan − 1)(sec tan ) (sec )2 = sec (sec2 − tan2 + tan ) sec 2 = 1 + tan sec (b) () = tan − 1 sec = sin cos − 1 1 cos = sin − cos cos 1 cos = sin − cos ⇒ 0() = cos − (− sin ) = cos + sin (c) From part (a), 0() = 1 + tan sec = 1 sec + tan sec = cos + sin , which is the expression for 0() in part (b). 32. (a) () = () sin ⇒ 0() = () cos + sin · 0(), so 0( 3 ) = ( 3 ) cos 3 + sin 3 · 0( 3 ) = 4 · 1 2 + √23 · (−2) = 2 − √3 (b) () = cos () ⇒ 0() = () · (− sin[()−)]2cos · 0(), so 0( 3 ) = ( 3 ) · (− sin3)3−cos 2 3 · 0( 3 ) = 4− √234−2 1 2(−2) = −2 √163 + 1 = 1 −16 2 √3 33. () = + 2 sin has a horizontal tangent when 0() = 0 ⇔ 1 + 2 cos = 0 ⇔ cos = − 1 2 ⇔ = 2 3 + 2 or 43 + 2, where is an integer. Note that 43 and 23 are ± 3 units from . This allows us to write the solutions in the more compact equivalent form (2 + 1) ± 3 , an integer. 34. () = cos has a horizontal tangent when 0() = 0. 0() = (− sin ) + (cos ) = (cos − sin ). 0() = 0 ⇔ cos − sin = 0 ⇔ cos = sin ⇔ tan = 1 ⇔ = 4 + , an integer. 35. (a) () = 8 sin ⇒ () = 0() = 8 cos ⇒ () = 00() = −8 sin (b) The mass at time = 23 has position 23 = 8 sin 23 = 8 √23 = 4√3, velocity 23 = 8 cos 23 = 8− 1 2 = −4, and acceleration 23 = −8 sin 23 = −8 √23 = −4 √3. Since 23 0, the particle is moving to the left. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.194 ¤ CHAPTER 3 DIFFERENTIATION RULES 36. (a) () = 2 cos + 3 sin ⇒ () = −2 sin + 3 cos ⇒ () = −2 cos − 3 sin (b) (c) = 0 ⇒ 2 ≈ 255. So the mass passes through the equilibrium position for the first time when ≈ 255 s. (d) = 0 ⇒ 1 ≈ 098, (1) ≈ 361 cm. So the mass travels a maximum of about 36 cm (upward and downward) from its equilibrium position. (e) The speed || is greatest when = 0, that is, when = 2 + , a positive integer. 37. From the diagram we can see that sin = 10 ⇔ = 10 sin . We want to find the rate of change of with respect to , that is, . Taking the derivative of = 10 sin , we get = 10(cos ). So when = 3 , = 10 cos 3 = 10 1 2 = 5 ftrad. 38. (a) = sin + cos ⇒ = ( sin + cos )(0) − ( cos − sin ) ( sin + cos )2 = (sin − cos ) ( sin + cos )2 (b) = 0 ⇔ (sin − cos ) = 0 ⇔ sin = cos ⇔ tan = ⇔ = tan−1 (c) From the graph of = 06(50) 06 sin + cos for 0 ≤ ≤ 1, we see that = 0 ⇒ ≈ 054. Checking this with part (b) and = 06, we calculate = tan−1 06 ≈ 054. So the value from the graph is consistent with the value in part (b). 39. lim →0 sin 5 3 = lim →0 5 3 sin 5 5 = 53 lim →0 sin 5 5 = 53 lim →0 sin [ = 5] = 53 · 1 = 53 40. lim →0 sin sin = lim →0 sin · sin · 1 = lim →0 sin · lim →0 sin · 1 [ = ] = 1 · lim →0 1 sin · 1 = 1 · 1 · 1 = 1 41. lim →0 tan 6 sin 2 = lim →0 sin 6 · cos 6 1 · sin 2 = lim →0 6 sin 6 6 · lim →0 cos 6 1 · lim →0 2 sin 2 2 = 6 lim →0 sin 6 6 · lim →0 1 cos 6 · 1 2 lim →0 2 sin 2 = 6(1) · 1 1 · 1 2 (1) = 3 42. lim →0 cos − 1 sin = lim →0 cos − 1 sin = lim →0 cos − 1 lim →0 sin = 0 1 = 0 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.3 DERIVATIVES OF TRIGONOMETRIC FUNCTIONS ¤ 195 43. lim →0 sin 3 53 − 4 = lim →0 sin 3 3 · 523− 4 = lim →0 sin 3 3 · lim →0 523− 4 = 1 · −34 = −3 4 44. lim →0 sin 3 sin 5 2 = lim →0 3 sin 3 3 · 5 sin 5 5 = lim →0 3 sin 3 3 · lim →0 5 sin 5 5 = 3 lim →0 sin 3 3 · 5 lim →0 sin 5 5 = 3(1) · 5(1) = 15 45. Divide numerator and denominator by . (sin also works.) lim →0 sin + tan = lim →0 sin 1 + sin · 1 cos = lim →0 sin 1 + lim →0 sin lim →0 cos 1 = 1 1 + 1 · 1 = 1 2 46. lim →0 csc sin(sin ) = lim →0 sin(sin ) sin = lim →0 sin [As → 0, = sin → 0.] = 1 47. lim →0 cos − 1 22 = lim →0 cos22− 1 · cos cos + 1 + 1 = lim →0 2cos 2(cos 2 −+ 1) 1 = lim →0 22−(cos sin2 + 1) = − 1 2 lim →0 sin · sin · 1 cos + 1 = − 1 2 lim →0 sin · lim →0 sin · lim →0 cos 1+ 1 = − 1 2 · 1 · 1 · 1 1 + 1 = − 1 4 48. lim →0 sin(2) = lim →0 · sin( ·2) = lim →0 · lim →0 sin( 22) = 0 · lim →0+ sin where = 2 = 0 · 1 = 0 49. lim →4 1 − tan sin − cos = lim →4 1 − cos sin · cos (sin − cos ) · cos = lim →4 (sincos −cos − sin ) cos = lim →4 cos −1 = 1−√12 = −√2 50. lim →1 sin( − 1) 2 + − 2 = lim →1 (sin( + 2)( − −1)1) = lim →1 + 2 1 lim →1 sin( −−11) = 1 3 · 1 = 1 3 51. (sin ) = cos ⇒ 22 (sin ) = − sin ⇒ 33 (sin ) = − cos ⇒ 44 (sin ) = sin . The derivatives of sin occur in a cycle of four. Since 99 = 4(24) + 3, we have 99 99 (sin ) = 33 (sin ) = − cos . 52. Let () = sin and () = sin , so () = (). Then 0() = () + 0(), 00() = 0() + 0() + 00() = 20() + 00(), 000() = 200() + 00() + 000() = 300() + 000() · · · ()() = (−1)() + ()(). Since 34 = 4(8) + 2, we have (34)() = (2)() = 2 2 (sin ) = − sin and (35)() = − cos . Thus, 35 35 ( sin ) = 35(34)() + (35)() = −35 sin − cos . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.196 ¤ CHAPTER 3 DIFFERENTIATION RULES 53. = sin + cos ⇒ 0 = cos − sin ⇒ 00 = − sin − cos . Substituting these expressions for , 0, and 00 into the given differential equation 00 + 0 − 2 = sin gives us (− sin − cos ) + (cos − sin ) − 2( sin + cos ) = sin ⇔ −3 sin − sin + cos − 3 cos = sin ⇔ (−3 − ) sin + ( − 3) cos = 1 sin , so we must have −3 − = 1 and − 3 = 0 (since 0 is the coefficient of cos on the right side). Solving for and , we add the first equation to three times the second to get = − 10 1 and = − 10 3 . 54. (a) Let = 1 . Then as → ∞, → 0+, and lim →∞ sin 1 = lim →0+ 1 sin = lim →0 sin = 1. (b) Since −1 ≤ sin (1) ≤ 1, we have (as illustrated in the figure) − || ≤ sin (1) ≤ ||. We know that lim →0 (||) = 0 and lim →0 (− ||) = 0; so by the Squeeze Theorem, lim →0 sin (1) = 0. (c) 55. (a) tan = sin cos ⇒ sec2 = cos cos − sin (− sin ) cos2 = cos2 + sin2 cos2 . So sec2 = cos12 . (b) sec = 1 cos ⇒ sec tan = (cos )(0) − 1(− sin ) cos2 . So sec tan = cos sin2 . (c) (sin + cos ) = 1 + cot csc ⇒ cos − sin = csc (− csc2 ) − (1 + cot )(− csc cot ) csc2 = csc [− csc2 + (1 + cot ) cot ] csc2 = − csc2 + cot2 + cot csc = −1 + cot csc So cos − sin = cot − 1 csc . 56. We get the following formulas for and in terms of : sin 2 = 10 ⇒ = 10 sin 2 and cos 2 = 10 ⇒ = 10 cos 2 Now () = 1 22 and () = 1 2(2) = . So lim →0+ () () = lim →0+ 12 2 = 12 lim →0+ = 12 lim →0+ 10 sin(2) 10 cos(2) = 12 lim →0+ tan(2) = 0 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.4 THE CHAIN RULE ¤ 197 57. By the definition of radian measure, = , where is the radius of the circle. By drawing the bisector of the angle , we can see that sin 2 = 2 ⇒ = 2 sin 2 . So lim →0+ = lim →0+ 2 sin(2) = lim →0+ 2 sin( 2 · ( 2) 2) = lim →0 sin( 22) = 1. [This is just the reciprocal of the limit lim →0 sin = 1 combined with the fact that as → 0, 2 → 0 also] 58. (a) It appears that () = √1 −cos 2 has a jump discontinuity at = 0. (b) Using the identity cos 2 = 1 − sin2, we have √1 −cos 2 = 1 − (1 − 2 sin2 ) = √2 sin 2 = √2 |sin |. Thus, lim →0− √1 − cos 2 = lim →0− √2 |sin | = √12 lim →0− −(sin ) = − 1 √ 2 lim →0− 1 sin = − 1 √ 2 · 1 1 = − √2 2 Evaluating lim →0+ () is similar, but | sin| = + sin , so we get 1 2√2. These values appear to be reasonable values for the graph, so they confirm our answer to part (a). Another method: Multiply numerator and denominator by √1 + cos 2. 3.4 The Chain Rule 1. Let = () = 1 + 4 and = () = √3 . Then = = ( 1 3−23)(4) = 33 (1 + 4 4 )2 . 2. Let = () = 23 + 5 and = () = 4. Then = = (43)(62) = 242(23 + 5)3. 3. Let = () = and = () = tan . Then = = (sec2 )() = sec2 . 4. Let = () = cot and = () = sin . Then = = (cos )(− csc2 ) = − cos(cot ) csc2 . 5. Let = () = √ and = () = . Then = = () 1 2−12 = √ · 2 √1 = 2√√. 6. Let = () = 2 − and = () = √. Then = = ( 1 2−12)(−) = −2√2− . 7. () = (56 + 23)4 ⇒ 0() = 4(56 + 23)3 · (56 + 23) = 4(56 + 23)3(305 + 62). We can factor as follows: 4(3)3(53 + 2)362(53 + 1) = 2411(53 + 2)3(53 + 1) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.198 ¤ CHAPTER 3 DIFFERENTIATION RULES 8. () = (1 + + 2)99 ⇒ 0() = 99(1 + + 2)98 · 1 + + 2 = 99(1 + + 2)98(1 + 2) 9. () = √5 + 1 = (5 + 1)12 ⇒ 0() = 1 2(5 + 1)−12(5) = 5 2√5 + 1 10. () = √3 21− 1 = (2 − 1)−13 ⇒ 0() = −13(2 − 1)−43(2) = 3(2−−21)43 11. () = cos(2) ⇒ 0() = − sin(2) · (2) = − sin(2) · (2) = −2 sin(2) 12. () = cos2 = (cos )2 ⇒ 0() = 2 (cos )1 (− sin ) = −2 sin cos = − sin 2 13. = 2−3 ⇒ 0 = 2−3(−3) + −3(2) = −3(−32 + 2) = −3(2 − 3) 14. () = sin ⇒ 0() = (cos ) · + (sin ) · 1 = cos + sin 15. () = sin ⇒ 0() = (cos ) · + (sin ) · = ( cos + sin ) 16. () = 2− ⇒ 0() = 2−(2 − 1) 17. () = (2 − 3)4(2 + + 1)5 ⇒ 0() = (2 − 3)4 · 5(2 + + 1)4(2 + 1) + (2 + + 1)5 · 4(2 − 3)3 · 2 = (2 − 3)3(2 + + 1)4[(2 − 3) · 5(2 + 1) + (2 + + 1) · 8] = (2 − 3)3(2 + + 1)4(202 − 20 − 15 + 82 + 8 + 8) = (2 − 3)3(2 + + 1)4(282 − 12 − 7) 18. () = (2 + 1)3(2 + 2)6 ⇒ 0() = (2 + 1)3 · 6(2 + 2)5 · 2 + (2 + 2)6 · 3(2 + 1)2 · 2 = 6(2 + 1)2(2 + 2)5[2(2 + 1) + (2 + 2)] = 6(2 + 1)2(2 + 2)5(32 + 4) 19. () = ( + 1)23(22 − 1)3 ⇒ 0() = ( + 1)23 · 3(22 − 1)2 · 4 + (22 − 1)3 · 2 3( + 1)−13 = 2 3( + 1)−13(22 − 1)2[18( + 1) + (22 − 1)] = 23 ( + 1)−13(22 − 1)2(202 + 18 − 1) 20. () = (3 − 1)4(2 + 1)−3 ⇒ 0() = (3 − 1)4(−3)(2 + 1)−4(2) + (2 + 1)−3 · 4(3 − 1)3(3) = 6(3 − 1)3(2 + 1)−4[−(3 − 1) + 2(2 + 1)] = 6(3 − 1)3(2 + 1)−4( + 3) 21. = + 1 = + 1 12 ⇒ 0 = 1 2 + 1 −12 + 1 = 12 ( + 1) −1−212 ( + 1)(1) ( + 1) −2 (1) = 1 2 ( + 1)12 12 1 ( + 1)2 = 1 2√( + 1)32 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.4 THE CHAIN RULE ¤ 199 22. = + 1 5 ⇒ 0 = 5 + 1 4 + 1 = 5 + 1 4 1 − 12 . Another form of the answer is 5(2 + 1)4(2 − 1) 6 . 23. = tan ⇒ 0 = tan (tan ) = (sec2 )tan 24. Using Formula 5 and the Chain Rule, () = 23 ⇒ 0() = 23 ln 2 (3) = 3(ln 2)223. 25. () = 3 3 − + 1 18 ⇒ 0() = 8 3 3 − + 1 17 3 3 − + 1 1 = 8 (3 3 − + 1) 177 (3 + 1)(3(23) −+ 1) (23 − 1)(32) = 8 (3 − 1)7 (3 + 1)7 32[(3 + 1) − (3 − 1)] (3 + 1)2 = 8((3 3 − + 1) 1)7 7 (33+ 1) 2(2) 2 = 48(23(+ 1) 3 −91)7 26. () = 1 + cos 1 + sin = 1 + cos 1 + sin 12 ⇒ 0() = 1 21 + cos 1 + sin −12 (1 + cos ) cos (1 + cos − (1 + sin )2 )(− sin ) = 1 2 (1 + sin )−12 (1 + cos )−12 cos + cos2 + sin + sin2 (1 + cos )2 = cos + sin + 1 2√1 + sin (1 + cos )32 27. Using Formula 5 and the Chain Rule, () = 102√ ⇒ 0() = 102√ ln 10 2√ = 102√ ln 10 2 · 1 2−12 = (ln 10) 10 √ 2√ 28. () = (−1) ⇒ 0() = (−1) − 1 = (−1) ( − 1)(1) − (1) ( − 1)2 = − (−1) ( − 1)2 29. () = (2 − 1)3 (2 + 1)5 ⇒ 0() = (2 + 1)5 · 3(2 − 1)2(2) − (2 − 1)3 · 5(2 + 1)4(2) [(2 + 1)5]2 = 2(2 + 1)4(2 − 1)2[3(2 + 1) − 5(2 − 1)] (2 + 1)10 = 2(2 − 1)2(62 + 3 − 52 + 5) (2 + 1)6 = 2(2 − 1)2(2 + 3 + 5) (2 + 1)6 30. () = tan2() = [tan()]2 ⇒ 0() = 2 [tan()]1 tan() = 2 tan() sec2() · = 2 tan() sec2() 31. By (9), () = sin 2 ⇒ 0() = sin 2( sin 2)0 = sin 2( · 2 cos 2 + sin 2 · 1) = sin 2(2 cos 2 + sin 2) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.200 ¤ CHAPTER 3 DIFFERENTIATION RULES 32. () = √32+ 1 ⇒ 0() = (3 + 1)12(2)−√32+ 1 · 1 2(32 + 1)−12(32) = (3 + 1)−1(23+ 1) 2(3 1+ 1) − 3 23 = 1 23 + 2 (3 + 1)32 = (3 + 4) 2(3 + 1)32 33. Using Formula 5 and the Chain Rule, () = 4 ⇒ 0() = 4 (ln 4) = −1 = 4 (ln 4) −−2 = − (ln 4) 4 2 34. () = 4 2 + 1 + 15 ⇒ 0() = 54 2 + 1 + 14 (2 + 1)(4(32)+ 1) − (24 + 1)(2) = 5(4 + 1)(422[2 + 1) 2(4(22+ 1) + 1) −2 (4 + 1)] = 10(4 + 1)4(4 + 22 − 1) (2 + 1)6 35. = cos11 + − 2 2 ⇒ 0 = − sin1 1 +− 2 2 · 1 1 +− 2 2 = − sin11 +− 2 2 · (1 + 2)(−2(1 + 2) −2(1 )2− 2)(22) = − sin1 1 +− 2 2 · −22 (1 + (1 +2) + (1 2)2 − 2) = − sin1 1 +− 2 2 · (1 + −222(2) )2 = (1 +422)2 · sin1 1 +− 2 2 36. = 2−1 ⇒ 0 = 2−112 + −1(2) = −1 + 2−1 = −1(1 + 2) 37. = cot2(sin ) = [cot(sin )]2 ⇒ 0 = 2[cot(sin )] · [cot(sin )] = 2 cot(sin ) · [− csc2(sin ) · cos ] = −2 cos cot(sin ) csc2(sin ) 38. = √1 + −2 ⇒ 0 = 1 21 + −2−12 −2−2 + −2 = −2(−2 + 1) 2 √1 + −2 39. () = tan(sec(cos )) ⇒ 0() = sec2(sec(cos )) sec(cos ) = sec2(sec(cos ))[sec(cos ) tan(cos )] cos = − sec2(sec(cos )) sec(cos ) tan(cos ) sin 40. = sin 2 + sin(2) ⇒ 0 = sin 2 sin 2 + cos(2) 2 = sin 2(cos 2) · 2 + cos(2) 2 · 2 = 2 cos 2 sin 2 + 22 cos(2) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.4 THE CHAIN RULE ¤ 201 41. () = sin2sin2 = sinsin22 ⇒ 0() = 2sinsin2 · sinsin2 = 2 sinsin2 · cossin2 · sin2 = 2 sinsin2 cossin2 · sin2 · sin2 = 2 sinsin2 cossin2 sin2 · 2 sin cos = 4 sinsin2 cossin2 sin2 sin cos 42. = + + √ ⇒ 0 = 1 2 + + √ −121 + 1 2 + √ −121 + 1 2−12 43. () = (2 + ) ⇒ 0() = (2 + )−1 · (2 + ) = (2 + )−1 · 2(ln ) · = 22(ln )(2 + )−1 44. = 234 ⇒ 0 = 234 (ln 2) 34 = 234 (ln 2) 34 (ln 3) 4 = 234 (ln 2) 34 (ln 3) 4(ln 4) = (ln 2)(ln 3)(ln 4)434234 45. = cos sin(tan ) = cos(sin(tan ))12 ⇒ 0 = − sin(sin(tan ))12 · (sin(tan ))12 = − sin(sin(tan ))12 · 1 2(sin(tan ))−12 · (sin(tan )) = − sin sin(tan ) 2 sin(tan ) · cos(tan ) · tan = −2sin sin(tan sin(tan ) ) · cos(tan ) · sec2() · = − cos(tan ) sec2() sin sin(tan ) 2 sin(tan ) 46. = + ( + sin2 )34 ⇒ 0 = 4 + ( + sin2 )33 · 1 + 3( + sin2 )2 · (1 + 2 sin cos ) 47. = cos(sin 3) ⇒ 0 = − sin(sin 3) · (cos 3) · 3 = −3 cos 3 sin(sin 3) ⇒ 00 = −3 [(cos 3) cos(sin 3)(cos 3) · 3 + sin(sin 3)(− sin 3) · 3] = −9 cos2(3) cos(sin 3) + 9(sin 3) sin(sin 3) 48. = 1 (1 + tan )2 = (1 + tan )−2 ⇒ 0 = −2(1 + tan )−3 sec2 = (1 + tan −2 sec2)3 . Using the Product Rule with 0 = −2(1 + tan )−3 (sec )2, we get 00 = −2(1 + tan )−3 · 2(sec )(sec tan ) + (sec )2 · 6(1 + tan )−4 sec2 = 2 sec2 (1 + tan )−4 −2(1 + tan ) tan + 3 sec2 2 is the lesser exponent for and −4 for (1 + tan sec ) = 2 sec2 (1 + tan )−4 −2 tan − 2 tan2 + 3(tan2 + 1) = 2 sec2 tan2 − 2 tan + 3 (1 + tan )4 49. = √1 − sec ⇒ 0 = 1 2(1 − sec )−12(− sec tan ) = − sec tan 2√1 − sec . Using the Product Rule with 0 = − 1 2 sec tan (1 − sec )−12, we get °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.202 ¤ CHAPTER 3 DIFFERENTIATION RULES 00 = − 1 2 sec tan − 1 2(1 − sec )−32(− sec tan ) + (1 − sec )−12 − 1 2[sec sec2 + tan sec tan ]. Now factor out − 1 2 sec (1 − sec )−32. Note that − 3 2 is the lesser exponent on (1 − sec ). Continuing, 00 = − 1 2 sec (1 − sec )−32 1 2 sec tan2 + (1 − sec )(sec2 + tan2 ) = − 12 sec (1 − sec )−32 1 2 sec tan2 + sec2 + tan2 − sec3 − sec tan2 = − 12 sec (1 − sec )−32 − 1 2 sec (sec2 − 1) + sec2 + (sec2 − 1) − sec3 = − 12 sec (1 − sec )−32 − 3 2 sec3 + 2 sec2 + 1 2 sec − 1 = sec (1 − sec )−32 3 4 sec3 − sec2 − 1 4 sec + 1 2 = sec (3 sec3 − 4 sec2 − sec + 2) 4(1 − sec )32 There are many other correct forms of 00, such as 00 = sec (3 sec + 2)√1 − sec 4 . We chose to find a factored form with only secants in the final form. 50. = ⇒ 0 = · ()0 = · ⇒ 00 = · ()0 + · 0 = · + · · = · (1 + ) or +(1 + ) 51. = 2 ⇒ 0 = 2 ln 2. At (0 1), 0 = 20 ln 2 = ln 2, and an equation of the tangent line is − 1 = (ln 2)( − 0) or = (ln 2) + 1. 52. = √1 + 3 = (1 + 3)12 ⇒ 0 = 1 2(1 + 3)−12 · 32 = 32 2√1 + 3 . At (2 3), 0 = 23√· 49 = 2, and an equation of the tangent line is − 3 = 2( − 2), or = 2 − 1. 53. = sin(sin ) ⇒ 0 = cos(sin ) · cos . At ( 0), 0 = cos(sin ) · cos = cos(0) · (−1) = 1(−1) = −1, and an equation of the tangent line is − 0 = −1( − ), or = − + . 54. = −2 ⇒ 0 = −2(−2) + −2(1) = −2(−22 + 1). At (0 0), 0 = 0(1) = 1, and an equation of the tangent line is − 0 = 1( − 0) or = . 55. (a) = 2 1 + − ⇒ 0 = (1 + −)(0) − 2(−−) (1 + −)2 = 2− (1 + −)2 . At (0 1), 0 = 20 (1 + 0)2 = 2(1) (1 + 1)2 = 2 22 = 1 2 . So an equation of the tangent line is − 1 = 1 2( − 0) or = 1 2 + 1. (b) 56. (a) For 0, || = , and = () = √2 − 2 ⇒ 0() = √2 − 2 (1) − 1 2(2 − 2)−12(−2) √2 − 2 2 · (2 − 2)12 (2 − 2)12 = (2 − 2) + 2 (2 − 2)32 = 2 (2 − 2)32 So at (1 1), the slope of the tangent line is 0(1) = 2 and its equation is − 1 = 2( − 1) or = 2 − 1. (b) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.4 THE CHAIN RULE ¤ 203 57. (a) () = √2 − 2 = (2 − 2)12 ⇒ 0() = · 1 2(2 − 2)−12(−2) + (2 − 2)12 · 1 = (2 − 2)−12 −2 + (2 − 2) = √2 2−−222 (b) 0 = 0 when has a horizontal tangent line, 0 is negative when is decreasing, and 0 is positive when is increasing. 58. (a) From the graph of , we see that there are 5 horizontal tangents, so there must be 5 zeros on the graph of 0. From the symmetry of the graph of , we must have the graph of 0 as high at = 0 as it is low at = . The intervals of increase and decrease as well as the signs of 0 are indicated in the figure. (b) () = sin( + sin 2) ⇒ 0() = cos(+sin 2)· (+sin 2) = cos(+sin 2)(1+ 2 cos 2) 59. For the tangent line to be horizontal, 0() = 0. () = 2 sin + sin2 ⇒ 0() = 2 cos + 2 sin cos = 0 ⇔ 2 cos (1 + sin ) = 0 ⇔ cos = 0 or sin = −1, so = 2 + 2 or 32 + 2, where is any integer. Now 2 = 3 and 32 = −1, so the points on the curve with a horizontal tangent are 2 + 2 3 and 32 + 2 −1, where is any integer. 60. = √1 + 2 ⇒ 0 = 1 2(1 + 2)−12 · 2 = √1 + 2 1 . The line 6 + 2 = 1 or = −3 + 1 2 has slope −3, so the tangent line perpendicular to it must have slope 1 3. Thus, 1 3 = 1 √1 + 2 ⇔ √1 + 2 = 3 ⇒ 1 + 2 = 9 ⇔ 2 = 8 ⇔ = 4. When = 4, = 1 + 2(4) = 3, so the point is (4 3). 61. () = (()) ⇒ 0() = 0(()) · 0(), so 0(5) = 0((5)) · 0(5) = 0(−2) · 6 = 4 · 6 = 24. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.204 ¤ CHAPTER 3 DIFFERENTIATION RULES 62. () = 4 + 3() ⇒ 0() = 1 2(4 + 3())−12 · 3 0(), so 0(1) = 1 2(4 + 3(1))−12 · 3 0(1) = 1 2(4 + 3 · 7)−12 · 3 · 4 = √625 = 6 5. 63. (a) () = (()) ⇒ 0() = 0(()) · 0(), so 0(1) = 0((1)) · 0(1) = 0(2) · 6 = 5 · 6 = 30. (b) () = (()) ⇒ 0() = 0(()) · 0(), so 0(1) = 0((1)) · 0(1) = 0(3) · 4 = 9 · 4 = 36. 64. (a) () = (()) ⇒ 0() = 0(()) · 0(), so 0(2) = 0((2)) · 0(2) = 0(1) · 5 = 4 · 5 = 20. (b) () = (()) ⇒ 0() = 0(()) · 0(), so 0(3) = 0((3)) · 0(3) = 0(2) · 9 = 7 · 9 = 63. 65. (a) () = (()) ⇒ 0() = 0(())0(). So 0(1) = 0((1))0(1) = 0(3)0(1). To find 0(3), note that is linear from (2 4) to (6 3), so its slope is 3 − 4 6 − 2 = − 1 4 . To find 0(1), note that is linear from (0 6) to (2 0), so its slope is 0 − 6 2 − 0 = −3. Thus, 0(3)0(1) = − 1 4(−3) = 3 4. (b) () = (()) ⇒ 0() = 0(()) 0(). So 0(1) = 0((1)) 0(1) = 0(2) 0(1), which does not exist since 0(2) does not exist. (c) () = (()) ⇒ 0() = 0(())0(). So 0(1) = 0((1))0(1) = 0(3)0(1). To find 0(3), note that is linear from (2 0) to (5 2), so its slope is 2 − 0 5 − 2 = 2 3 . Thus, 0(3)0(1) = 2 3(−3) = −2. 66. (a) () = (()) ⇒ 0() = 0(()) 0(). So 0(2) = 0((2)) 0(2) = 0(1) 0(2) ≈ (−1)(−1) = 1. (b) () = (2) ⇒ 0() = 0(2) · 2 = 0(2)(2). So 0(2) = 0(2 2)(2 · 2) = 4 0(4) ≈ 4(2) = 8. 67. The point (3 2) is on the graph of , so (3) = 2. The tangent line at (3 2) has slope ∆ ∆ = −4 6 = − 2 3 . () = () ⇒ 0() = 1 2[()]−12 · 0() ⇒ 0(3) = 1 2[(3)]−12 · 0(3) = 1 2(2)−12(− 2 3) = − 1 3√2 or − 1 6√2. 68. (a) () = () ⇒ 0() = 0() () = 0()−1 (b) () = [()] ⇒ 0() = [()]−1 0() 69. (a) () = () ⇒ 0() = 0() () = 0() (b) () = () ⇒ 0() = () () = () 0() 70. (a) () = + () ⇒ 0() = · + 0() ⇒ 0(0) = 0 · + 0(0) = + 5. 0() = + 0() ⇒ 00() = · + 00() ⇒ 00(0) = 20 + 00(0) = 2 − 2. (b) () = () ⇒ 0() = 0() + () · ⇒ 0(0) = 0 0(0) + (0) · 0 = 5 + 3. An equation of the tangent line to the graph of at the point (0 (0)) = (0 (0)) = (0 3) is − 3 = (5 + 3)( − 0) or = (5 + 3) + 3. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.4 THE CHAIN RULE ¤ 205 71. () = ((())) ⇒ 0() = 0((())) · 0(()) · 0(), so 0(1) = 0(((1))) · 0((1)) · 0(1) = 0((2)) · 0(2) · 4 = 0(3) · 5 · 4 = 6 · 5 · 4 = 120 72. () = (2) ⇒ 0() = 0(2) 2 + (2) · 1 = 220(2) + (2) ⇒ 00() = 2200(2) 2 + 0(2) 4 + 0(2) 2 = 4300(2) + 40(2) + 20(2) = 60(2) + 4300(2) 73. () = (3(4())) ⇒ 0() = 0(3(4())) · (3(4())) = 0(3(4())) · 3 0(4()) · (4()) = 0(3(4())) · 3 0(4()) · 4 0(), so 0(0) = 0(3(4(0))) · 3 0(4(0)) · 4 0(0) = 0(3(4 · 0)) · 3 0(4 · 0) · 4 · 2 = 0(3 · 0) · 3 · 2 · 4 · 2 = 2 · 3 · 2 · 4 · 2 = 96. 74. () = ((())) ⇒ 0() = 0((())) · ((())) = 0((())) · · 0(()) · (()) + (()) · 1 = 0((())) · [ 0(()) · ( 0() + () · 1) + (())] , so 0(1) = 0(((1))) · [ 0((1)) · ( 0(1) + (1)) + ((1))] = 0((2)) · [ 0(2) · (4 + 2) + (2)] = 0(3) · [5 · 6 + 3] = 6 · 33 = 198. 75. = 2( cos 3 + sin 3) ⇒ 0 = 2(−3 sin 3 + 3 cos 3) + ( cos 3 + sin 3) · 22 = 2(−3 sin 3 + 3 cos 3 + 2 cos 3 + 2 sin 3) = 2[(2 + 3) cos 3 + (2 − 3) sin 3] ⇒ 00 = 2[−3(2 + 3) sin 3 + 3(2 − 3) cos 3] + [(2 + 3) cos 3 + (2 − 3) sin 3] · 22 = 2{[−3(2 + 3) + 2(2 − 3)] sin 3 + [3(2 − 3) + 2(2 + 3)] cos 3} = 2[(−12 − 5) sin 3 + (−5 + 12) cos 3] Substitute the expressions for , 0, and 00 in 00 − 40 + 13 to get 00 − 40 + 13 = 2[(−12 − 5) sin 3 + (−5 + 12) cos 3] − 42[(2 + 3) cos 3 + (2 − 3) sin 3] + 132( cos 3 + sin 3) = 2[(−12 − 5 − 8 + 12 + 13) sin 3 + (−5 + 12 − 8 − 12 + 13) cos 3] = 2[(0) sin 3 + (0) cos 3] = 0 Thus, the function satisfies the differential equation 00 − 40 + 13 = 0. 76. = ⇒ 0 = ⇒ 00 = 2. Substituting , 0, and 00 into 00 − 40 + = 0 gives us 2 − 4 + = 0 ⇒ (2 − 4 + 1) = 0. Since 6= 0, we must have 2 − 4 + 1 = 0 ⇒ = 4 ± √16 − 4 2 = 2 ± √3. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.206 ¤ CHAPTER 3 DIFFERENTIATION RULES 77. The use of , 2, , is just a derivative notation (see text page 159). In general, (2) = 2 0(2), 2(2) = 4 00(2), , (2) = 2 ()(2). Since () = cos and 50 = 4(12) + 2, we have (50)() = (2)() = − cos , so 50 cos 2 = −250 cos 2. 78. () = −, 0() = − − − = (1 − )−, 00() = −− + (1 − )(−−) = ( − 2)−. Similarly, 000() = (3 − )−, (4)() = ( − 4)−, , (1000)() = ( − 1000)−. 79. () = 10 + 1 4 sin(10) ⇒ the velocity after seconds is () = 0() = 1 4 cos(10)(10) = 52 cos(10) cms. 80. (a) = cos( + ) ⇒ velocity = 0 = − sin( + ). (b) If 6= 0 and 6= 0, then 0 = 0 ⇔ sin( + ) = 0 ⇔ + = ⇔ = − , an integer. 81. (a) () = 40 + 035 sin 2 54 ⇒ = 035 cos 25 4 524 = 0574 cos 25 4 = 754 cos 25 4 (b) At = 1, = 7 54 cos 2 54 ≈ 016. 82. () = 12 + 28 sin 365 2 ( − 80) ⇒ 0() = 28 cos 365 2 ( − 80) 365 2 . On March 21, = 80, and 0(80) ≈ 00482 hours per day. On May 21, = 141, and 0(141) ≈ 002398, which is approximately one-half of 0(80). 83. () = 2−15 sin 2 ⇒ () = 0() = 2[−15(cos 2)(2) + (sin 2)−15(−15)] = 2−15(2 cos 2 − 15 sin 2) 84. (a) lim →∞ () = lim →∞ 1 1 + − = 1 1 + · 0 = 1, since 0 ⇒ − → −∞ ⇒ − → 0. (b) () = (1 + −)−1 ⇒ = −(1 + −)−2(−−) = (1 + −− )2 (c) From the graph of () = (1 + 10−05)−1, it seems that () = 08 (indicating that 80% of the population has heard the rumor) when ≈ 74 hours. 85. (a) Use () = with = 00225 and = −00467 to get 0() = ( · + · 1) = ( + 1). 0(10) = 00225(0533)−0467 ≈ 00075, so the BAC was increasing at approximately 00075 (mgmL)min after 10 minutes. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.4 THE CHAIN RULE ¤ 207 (b) A half an hour later gives us = 10 + 30 = 40. 0(40) = 00225(−0868)−1868 ≈ −00030, so the BAC was decreasing at approximately 00030 (mgmL)min after 40 minutes. 86. () = (143653) · (101395) ⇒ 0() = (143653) · (101395)(ln 101395). The units for 0() are millions of people per year. The rates of increase for 1920, 1950, and 2000 are 0(20) ≈ 2625, 0(50) ≈ 3978, and 0(100) ≈ 7953, respectively. 87. By the Chain Rule, () = = = () = () . The derivative is the rate of change of the velocity with respect to time (in other words, the acceleration) whereas the derivative is the rate of change of the velocity with respect to the displacement. 88. (a) The derivative represents the rate of change of the volume with respect to the radius and the derivative represents the rate of change of the volume with respect to time. (b) Since = 4 3 3, = = 42 . 89. (a) Using a calculator or CAS, we obtain the model = with ≈ 1000124369 and ≈ 0000045145933. (b) Use 0() = ln (from Formula 5) with the values of and from part (a) to get 0(004) ≈ −67063 A. The result of Example 2.1.2 was −670 A. 90. (a) = with = 4502714 × 10−20 and = 1029953851, where is measured in thousands of people. The fit appears to be very good. (b) For 1800: 1 = 5308 − 3929 1800 − 1790 = 1379, 2 = 7240 1810 −− 5308 1800 = 1932. So 0(1800) ≈ (1 + 2)2 = 16555 thousand peopleyear. For 1850: 1 = 23,192 − 17,063 1850 − 1840 = 6129, 2 = 311860 ,443 −− 23 1850 ,192 = 8251. So 0(1850) ≈ (1 + 2)2 = 719 thousand peopleyear. (c) Using 0() = ln (from Formula 7) with the values of and from part (a), we get 0(1800) ≈ 15685 and 0(1850) ≈ 68607. These estimates are somewhat less than the ones in part (b). (d) (1870) ≈ 41,94656. The difference of 34 million people is most likely due to the Civil War (1861–1865). 91. (a) Derive gives 0() = 45( − 2)8 (2 + 1)10 without simplifying. With either Maple or Mathematica, we first get 0() = 9 ( − 2)8 (2 + 1)9 − 18(2( −+ 1) 2)910 , and the simplification command results in the expression given by Derive. (b) Derive gives 0 = 2(3 − + 1)3(2 + 1)4(173 + 62 − 9 + 3) without simplifying. With either Maple or Mathematica, we first get 0 = 10(2 + 1)4(3 − + 1)4 + 4(2 + 1)5(3 − + 1)3(32 − 1). If we use °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.208 ¤ CHAPTER 3 DIFFERENTIATION RULES Mathematica’s Factor or Simplify, or Maple’s factor, we get the above expression, but Maple’s simplify gives the polynomial expansion instead. For locating horizontal tangents, the factored form is the most helpful. 92. (a) () = 4 4 − + + 1 + 112. Derive gives 0() = ((34+4 − + 1)( 1) 4 44− +− + 1 + 1 + 1) whereas either Maple or Mathematica give 0 () = 4 4 − + + 1 + 1 34 (−41+ + 1)2 after simplification. (b) 0() = 0 ⇔ 34 − 1 = 0 ⇔ = ±4 1 3 ≈ ±07598. (c) Yes. 0() = 0 where has horizontal tangents. 0 has two maxima and one minimum where has inflection points. 93. (a) If is even, then () = (−). Using the Chain Rule to differentiate this equation, we get 0() = 0(−) (−) = − 0(−). Thus, 0(−) = − 0(), so 0 is odd. (b) If is odd, then () = −(−). Differentiating this equation, we get 0() = − 0(−)(−1) = 0(−), so 0 is even. 94. (())0 = () [()]−10 = 0() [()]−1 + (−1) [()]−2 0()() = 0() () − ()0() [()]2 = 0()() − ()0() [()]2 This is an alternative derivation of the formula in the Quotient Rule. But part of the purpose of the Quotient Rule is to show that if and are differentiable, so is . The proof in Section 3.2 does that; this one doesn’t. 95. (a) (sin cos ) = sin−1 cos cos + sin (− sin ) [Product Rule] = sin−1 (cos cos − sin sin ) [factor out sin−1 ] = sin−1 cos( + ) [Addition Formula for cosine] = sin−1 cos[( + 1)] [factor out ] (b) (cos cos ) = cos−1 (− sin ) cos + cos (− sin ) [Product Rule] = − cos−1 (cos sin + sin cos ) [factor out − cos−1 ] = − cos−1 sin( + ) [Addition Formula for sine] = − cos−1 sin[( + 1)] [factor out ] 96. “The rate of change of 5 with respect to is eighty times the rate of change of with respect to ” ⇔ 5 = 80 ⇔ 54 = 80 ⇔ 54 = 80 (Note that 6= 0 since the curve never has a horizontal tangent) ⇔ 4 = 16 ⇔ = 2 (since 0 for all ) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.APPLIED PROJECT WHERE SHOULD A PILOT START DESCENT? ¤ 209 97. Since ◦ = 180 rad, we have (sin ◦) = sin 180 = 180 cos 180 = 180 cos ◦. 98. (a) () = || = √2 = (2)12 ⇒ 0() = 1 2(2)−12(2) = √2 = || for 6= 0. is not differentiable at = 0. (b) () = |sin | = √sin2 ⇒ 0() = 1 2(sin2 )−122 sin cos = sin |sin | cos = cos − cos if if sin sin 0 0 is not differentiable when = , an integer. (c) () = sin || = sin √2 ⇒ 0() = cos || · || = || cos = cos − cos if if 0 0 is not differentiable at 0. 99. The Chain Rule says that = , so 2 2 = = = + [Product Rule] = + 22 = 22 2 + 22 100. From Exercise 99, 2 2 = 2 2 2 + 22 ⇒ 3 3 = 2 2 = 22 2 + 22 = 22 2 + 2 22 + 22 + 22 = 22 2 + 2 22 22 + 22 + 33 = 3 3 3 + 3 22 22 + 33 APPLIED PROJECT Where Should a Pilot Start Descent? 1. Condition (i) will hold if and only if all of the following four conditions hold: () (0) = 0 () 0(0) = 0 (for a smooth landing) () 0() = 0 (since the plane is cruising horizontally when it begins its descent) () () = . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.210 ¤ CHAPTER 3 DIFFERENTIATION RULES First of all, condition implies that (0) = = 0, so () = 3 + 2 + ⇒ 0() = 32 + 2 + . But 0(0) = = 0 by condition . So 0() = 32 + 2 = (3 + 2). Now by condition , 3 + 2 = 0 ⇒ = −2 3. Therefore, () = −2 3 3 + 2. Setting () = for condition , we get () = −23 3 + 2 = ⇒ − 2 3 2 + 2 = ⇒ 1 3 2 = ⇒ = 3 2 ⇒ = − 2 3 . So = () = −23 3 + 32 2. 2. By condition (ii), = − for all , so () = − . Condition (iii) states that 2 2 ≤ . By the Chain Rule, we have = = − 2 3 32 + 32 (2) = 6 32 − 6 2 (for ≤ ) ⇒ 2 2 = 6 3 (2) − 6 2 = −12 3 2 + 6 2 2 . In particular, when = 0, = and so 2 2 =0 = − 122 3 + 6 2 2 = −6 2 2 . Thus, 22 =0 = 6 2 2 ≤ . (This condition also follows from taking = 0.) 3. We substitute = 860 mih2, = 35,000 ft × 1 mi 5280 ft, and = 300 mih into the result of part (b): 635,000 · 5280 1 (300)2 2 ≤ 860 ⇒ ≥ 300 6 · 5280 35,000 · 860 ≈ 645 miles. 4. Substituting the values of and in Problem 3 into () = −2 3 3 + 32 2 gives us () = 3 + 2, where ≈ −4937 × 10−5 and ≈ 478 × 10−3. 3.5 Implicit Differentiation 1. (a) (92 − 2) = (1) ⇒ 18 − 2 0 = 0 ⇒ 2 0 = 18 ⇒ 0 = 9 (b) 92 − 2 = 1 ⇒ 2 = 92 − 1 ⇒ = ±√92 − 1, so 0 = ± 1 2(92 − 1)−12(18) = ±√992− 1. (c) From part (a), 0 = 9 = 9 ±√92 − 1, which agrees with part (b). 2. (a) (22 + + ) = (1) ⇒ 4 + 1 + 0 + · 1 = 0 ⇒ 0 = −4 − − 1 ⇒ 0 = −4 + + 1 (b) 22 + + = 1 ⇒ = 1 − 22 − ⇒ = 1 − 2 − 1, so 0 = − 1 2 − 2 (c) From part (a), 0 = −4 + + 1 = −4 − 1 − 1 = −4 − 1 1 − 2 − 1 − 1 = −4 − 12 + 2 + 1 − 1 = −12 − 2, which agrees with part (b). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.5 IMPLICIT DIFFERENTIATION ¤ 211 3. (a) √ + √ = (1) ⇒ 12−12 + 1 2−120 = 0 ⇒ 2√1 0 = −2√1 ⇒ 0 = −√√ (b) √ + √ = 1 ⇒ √ = 1 − √ ⇒ = (1 − √ )2 ⇒ = 1 − 2√ + , so 0 = −2 · 1 2 −12 + 1 = 1 − √1. (c) From part (a), 0 = − √ √ = − 1 − √ √ [from part (b)] = −√1 + 1, which agrees with part (b). 4. (a) 2 − 1 = (4) ⇒ −2−2 + −20 = 0 ⇒ 12 0 = 22 ⇒ 0 = 222 (b) 2 − 1 = 4 ⇒ 1 = 2 − 4 ⇒ 1 = 2 − 4 ⇒ = 2 − 4, so 0 = (2 − 4)(1) − (−4) (2 − 4)2 = 2 (2 − 4)2 or 2(1 −12)2 . (c) From part (a), 0 = 22 2 = 22 −42 2 [from part (b)] = 2(22−24)2 = (2 −24)2 , which agrees with part (b). 5. (2 − 4 + 2) = (4) ⇒ 2 − 4[0 + (1)] + 2 0 = 0 ⇒ 2 0 − 40 = 4 − 2 ⇒ 0( − 2) = 2 − ⇒ 0 = 2 − − 2 6. (22 + − 2) = (2) ⇒ 4 + 0 + (1) − 2 0 = 0 ⇒ 0 − 2 0 = −4 − ⇒ ( − 2)0 = −4 − ⇒ 0 = −4 − − 2 7. (4 + 22 + 3) = (5) ⇒ 43 + 2 · 2 0 + 2 · 2 + 320 = 0 ⇒ 22 0 + 320 = −43 − 22 ⇒ (22 + 32)0 = −43 − 22 ⇒ 0 = −43 − 22 22 + 32 = − 2(22 + 2) (22 + 3) 8. (3 − 2 + 3) = (1) ⇒ 32 − · 2 0 − 2 · 1 + 320 = 0 ⇒ 320 − 2 0 = 2 − 32 ⇒ (32 − 2) 0 = 2 − 32 ⇒ 0 = 2 − 32 32 − 2 = 2 − 32 (3 − 2) 9. +2 = (2 + 1) ⇒ ( + )(2 ()+−)22(1 + 0) = 2 0 ⇒ 22 + 2 − 2 − 2 0 = 2( + )2 0 ⇒ 2 + 2 = 2( + )2 0 + 2 0 ⇒ ( + 2) = [2(2 + 2 + 2) + 2] 0 ⇒ 0 = ( + 2) 22 + 42 + 23 + 2 Or: Start by clearing fractions and then differentiate implicitly. 10. () = ( − ) ⇒ 0 + · 1 = 1 − 0 ⇒ 0 + 0 = 1 − ⇒ 0( + 1) = 1 − ⇒ 0 = 1 − + 1 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.212 ¤ CHAPTER 3 DIFFERENTIATION RULES 11. ( cos ) = (2 + 2) ⇒ (− sin ) + cos · 0 = 2 + 2 0 ⇒ cos · 0 − 2 0 = 2 + sin ⇒ 0(cos − 2) = 2 + sin ⇒ 0 = 2 + sin cos − 2 12. cos() = (1 + sin ) ⇒ − sin()(0 + · 1) = cos · 0 ⇒ −0 sin() − cos · 0 = sin() ⇒ 0[− sin() − cos ] = sin() ⇒ 0 = sin() − sin() − cos = − sin() sin() + cos 13. √ + = 4 + 4 ⇒ 1 2 ( + )−12 (1 + 0) = 43 + 430 ⇒ 1 2√ + + 1 2√ + 0 = 43 + 430 ⇒ 2√1+ − 43 = 430 − 2√1+ 0 ⇒ 1 − 83√ + 2√ + = 83√ + − 1 2√ + 0 ⇒ 0 = 18−3√83+√ +− 1 14. ( sin ) = ( + ) ⇒ cos + sin · 0 = 1 + 0 + · 1 ⇒ sin · 0 − 0 = 1 + − cos ⇒ 0( sin − ) = 1 + − cos ⇒ 0 = 1 + − cos sin − 15. () = ( − ) ⇒ · = 1 − 0 ⇒ · · 1 − · 0 2 = 1 − 0 ⇒ · 1 − 2 · 0 = 1 − 0 ⇒ 0 − 2 · 0 = 1 − ⇒ 01 − 2 = − ⇒ 0 = − 2 − 2 = ( − ) 2 − 16. () = 2 + 2 ⇒ 0 + (1) = 1 2 2 + 2−12 (2 + 2 0) ⇒ 0 + = 2+ 2 + 2+ 2 0 ⇒ 0 − 2+ 2 0 = 2+ 2 − ⇒ 2 + 2 − 2 + 2 0 = −2 +2+2 2 ⇒ 0 = −2+22+−2 17. tan−1(2) = ( + 2) ⇒ 1 + (12)2 (20 + · 2) = 1 + · 2 0 + 2 · 1 ⇒ 2 1 + 42 0 − 2 0 = 1 + 2 − 1 +2 42 ⇒ 01 +242 − 2 = 1 + 2 − 1 +2 42 ⇒ 0 = 1 + 2 − 2 1 + 42 2 1 + 42 − 2 or 0 = 1 + 42 + 2 + 44 − 2 2 − 2 − 253 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.5 IMPLICIT DIFFERENTIATION ¤ 213 18. ( sin + sin ) = (1) ⇒ cos · 0 + sin · 1 + cos + sin · 0 = 0 ⇒ cos · 0 + sin · 0 = − sin − cos ⇒ 0( cos + sin ) = − sin − cos ⇒ 0 = − sin − cos cos + sin 19. sin() = cos( + ) ⇒ cos() · (0 + · 1) = − sin( + ) · (1 + 0) ⇒ cos() 0 + cos() = − sin( + ) − 0 sin( + ) ⇒ cos() 0 + 0 sin( + ) = − cos() − sin( + ) ⇒ [ cos() + sin( + )] 0 = −1 [ cos() + sin( + )] ⇒ 0 = − cos() + sin( + ) cos() + sin( + ) 20. tan( − ) = 1 + 2 ⇒ (1 + 2) tan( − ) = ⇒ (1 + 2) sec2( − ) · (1 − 0) + tan( − ) · 2 = 0 ⇒ (1 + 2) sec2( − ) − (1 + 2) sec2( − ) · 0 + 2 tan( − ) = 0 ⇒ (1 + 2) sec2( − ) + 2 tan( − ) = 1 + (1 + 2) sec2( − ) · 0 ⇒ 0 = (1 + 2) sec2( − ) + 2 tan( − ) 1 + (1 + 2) sec2( − ) 21. () + 2[()]3 = (10) ⇒ 0() + 2 · 3[()]2 · 0() + [()]3 · 2 = 0. If = 1, we have 0(1) + 12 · 3[(1)]2 · 0(1) + [(1)]3 · 2(1) = 0 ⇒ 0(1) + 1 · 3 · 22 · 0(1) + 23 · 2 = 0 ⇒ 0(1) + 12 0(1) = −16 ⇒ 13 0(1) = −16 ⇒ 0(1) = − 16 13. 22. [() + sin ()] = (2) ⇒ 0() + cos () · 0() + sin () · 1 = 2. If = 0, we have 0(0) + 0 + sin (0) = 2(0) ⇒ 0(0) + sin 0 = 0 ⇒ 0(0) + 0 = 0 ⇒ 0(0) = 0. 23. (42 − 3 + 23) = (0) ⇒ 4 · 2 + 2 · 43 0 − (3 · 1 + · 32 0) + 2( · 32 + 3 · 0) = 0 ⇒ 432 0 − 32 0 + 23 0 = −24 + 3 − 62 ⇒ (432 − 32 + 23) 0 = −24 + 3 − 62 ⇒ 0 = = −24 + 3 − 62 432 − 32 + 23 24. ( sec ) = ( tan ) ⇒ · sec tan · 0 + sec · 1 = · sec2 + tan · 0 ⇒ sec tan · 0 − tan · 0 = sec2 − sec ⇒ ( sec tan − tan ) 0 = sec2 − sec ⇒ 0 = = sec2 − sec sec tan − tan 25. sin 2 = cos 2 ⇒ · cos 2 · 2 + sin 2 · 0 = (− sin 2 · 20) + cos(2) · 1 ⇒ sin 2 · 0 + 2 sin 2 · 0 = −2 cos 2 + cos 2 ⇒ 0(sin 2 + 2 sin 2) = −2 cos 2 + cos 2 ⇒ °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.214 ¤ CHAPTER 3 DIFFERENTIATION RULES 0 = −2 cos 2 + cos 2 sin 2 + 2 sin 2 . When = 2 and = 4 , we have 0 = (−2)(−1) + 0 0 + · 1 = 2 = 1 2 , so an equation of the tangent line is − 4 = 1 2( − 2 ), or = 1 2. 26. sin( + ) = 2 − 2 ⇒ cos( + ) · (1 + 0) = 2 − 20 ⇒ cos( + ) · 0 + 20 = 2 − cos( + ) ⇒ 0[cos( + ) + 2] = 2 − cos( + ) ⇒ 0 = 2 − cos( + ) cos( + ) + 2. When = and = , we have 0 = 21 + 2 − 1 = 1 3, so an equation of the tangent line is − = 1 3( − ), or = 1 3 + 23 . 27. 2 − − 2 = 1 ⇒ 2 − (0 + · 1) − 2 0 = 0 ⇒ 2 − 0 − − 2 0 = 0 ⇒ 2 − = 0 + 2 0 ⇒ 2 − = ( + 2) 0 ⇒ 0 = 2 − + 2 . When = 2 and = 1, we have 0 = 4 − 1 2 + 2 = 3 4 , so an equation of the tangent line is − 1 = 3 4( − 2), or = 3 4 − 1 2. 28. 2 + 2 + 42 = 12 ⇒ 2 + 2 0 + 2 + 8 0 = 0 ⇒ 2 0 + 8 0 = −2 − 2 ⇒ ( + 4) 0 = − − ⇒ 0 = − + + 4 . When = 2 and = 1, we have 0 = −2 + 1 2 + 4 = −12, so an equation of the tangent line is − 1 = − 1 2( − 2) or = − 1 2 + 2. 29. 2 + 2 = (22 + 22 − )2 ⇒ 2 + 2 0 = 2(22 + 22 − )(4 + 4 0 − 1). When = 0 and = 1 2, we have 0 + 0 = 2( 1 2)(20 − 1) ⇒ 0 = 20 − 1 ⇒ 0 = 1, so an equation of the tangent line is − 1 2 = 1( − 0) or = + 1 2. 30. 23 + 23 = 4 ⇒ 2 3−13 + 2 3−130 = 0 ⇒ √31 + 30 = 0 ⇒ 0 = − √33 . When = −3 √3 and = 1, we have 0 = − 1 −3 √3 13 = − −3 √3 23 −3 √3 = 3 3 √3 = 1 √ 3 , so an equation of the tangent line is − 1 = √13 + 3 √3 or = √13 + 4. 31. 2(2 + 2)2 = 25(2 − 2) ⇒ 4(2 + 2)(2 + 2 0) = 25(2 − 2 0) ⇒ 4( + 0)(2 + 2) = 25( − 0) ⇒ 4 0(2 + 2) + 250 = 25 − 4(2 + 2) ⇒ 0 = 25 − 4(2 + 2) 25 + 4(2 + 2) . When = 3 and = 1, we have 0 = 75 25 + 40 − 120 = − 45 65 = − 13 9 , so an equation of the tangent line is − 1 = − 13 9 ( − 3) or = − 13 9 + 40 13. 32. 2(2 − 4) = 2(2 − 5) ⇒ 4 − 42 = 4 − 52 ⇒ 43 0 − 8 0 = 43 − 10. When = 0 and = −2, we have −320 + 160 = 0 ⇒ −160 = 0 ⇒ 0 = 0, so an equation of the tangent line is + 2 = 0( − 0) or = −2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.5 IMPLICIT DIFFERENTIATION ¤ 215 33. (a) 2 = 54 − 2 ⇒ 2 0 = 5(43) − 2 ⇒ 0 = 103 − . So at the point (1 2) we have 0 = 10(1)3 − 1 2 = 9 2 , and an equation of the tangent line is − 2 = 9 2( − 1) or = 9 2 − 5 2. (b) 34. (a) 2 = 3 + 32 ⇒ 2 0 = 32 + 3(2) ⇒ 0 = 32 + 6 2 . So at the point (1 −2) we have 0 = 3(1)2 + 6(1) 2(−2) = − 9 4 , and an equation of the tangent line is + 2 = − 9 4( − 1) or = − 9 4 + 1 4. (b) The curve has a horizontal tangent where 0 = 0 ⇔ 32 + 6 = 0 ⇔ 3( + 2) = 0 ⇔ = 0 or = −2. But note that at = 0, = 0 also, so the derivative does not exist. At = −2, 2 = (−2)3 + 3(−2)2 = −8 + 12 = 4, so = ±2. So the two points at which the curve has a horizontal tangent are (−2 −2) and (−2 2). (c) 35. 2 + 42 = 4 ⇒ 2 + 8 0 = 0 ⇒ 0 = −(4) ⇒ 00 = −1 4 · 1 − · 0 2 = − 1 4 − [−(4)] 2 = − 1 4 42 + 2 43 = − 1 4 4 43 original equation since and must satisfy the 2 + 42 = 4 Thus, 00 = − 1 43 . 36. 2 + + 2 = 3 ⇒ 2 + 0 + + 2 0 = 0 ⇒ ( + 2)0 = −2 − ⇒ 0 = −2 − + 2 . Differentiating 2 + 0 + + 2 0 = 0 to find 00 gives 2 + 00 + 0 + 0 + 2 00 + 200 = 0 ⇒ ( + 2) 00 = −2 − 20 − 2(0)2 = −2 1 − 2+ 2 + + 2+ 2 + 2 ⇒ 00 = − 2 + 2 ( + 2)2 − (2(+ + 2 )(+ 2 )2 ) + (2 + )2 = − 2 ( + 2)3 (2 + 4 + 42 − 22 − 4 − − 22 + 42 + 4 + 2) = − 2 ( + 2)3 (32 + 3 + 32) = −( + 2 2 )3 (9) original equation since and must satisfy the 2 + + 2 = 3 Thus, 00 = − 18 ( + 2)3 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.216 ¤ CHAPTER 3 DIFFERENTIATION RULES 37. sin + cos = 1 ⇒ cos · 0 − sin = 0 ⇒ 0 = sin cos ⇒ 00 = cos cos − sin (− sin ) 0 (cos )2 = cos cos + sin sin (sin cos ) cos2 = cos2 cos + sin2 sin cos2 cos = cos2 cos + sin2 sin cos3 Using sin + cos = 1, the expression for 00 can be simplified to 00 = (cos2 + sin ) cos3 38. 3 − 3 = 7 ⇒ 32 − 320 = 0 ⇒ 0 = 2 2 ⇒ 00 = 2(2) − 2(2 0) (2)2 = 2[ − (22)] 4 = 2( − 32) 3 = 2(3 − 3) 32 = 2(−7) 5 = −14 5 39. If = 0 in + = , then we get 0 + = , so = 1 and the point where = 0 is (0 1). Differentiating implicitly with respect to gives us 0 + · 1 + 0 = 0. Substituting 0 for and 1 for gives us 0 + 1 + 0 = 0 ⇒ 0 = −1 ⇒ 0 = −1. Differentiating 0 + + 0 = 0 implicitly with respect to gives us 00 + 0 · 1 + 0 + 00 + 0 · 0 = 0. Now substitute 0 for , 1 for , and −1 for 0. 0 + −1 + −1 + 00 + −1 () −1 = 0 ⇒ −2 + 00 + 1 = 0 ⇒ 00 = 1 ⇒ 00 = 12 . 40. If = 1 in 2 + + 3 = 1, then we get 1 + + 3 = 1 ⇒ 3 + = 0 ⇒ (2 + 1) ⇒ = 0, so the point where = 1 is (1 0). Differentiating implicitly with respect to gives us 2 + 0 + · 1 + 32 · 0 = 0. Substituting 1 for and 0 for gives us 2 + 0 + 0 + 0 = 0 ⇒ 0 = −2. Differentiating 2 + 0 + + 320 = 0 implicitly with respect to gives us 2 + 00 + 0 · 1 + 0 + 3(200 + 0 · 20) = 0. Now substitute 1 for , 0 for , and −2 for 0. 2 + 00 + (−2) + (−2) + 3(0 + 0) = 0 ⇒ 00 = 2. Differentiating 2 + 00 + 20 + 3200 + 6(0)2 = 0 implicitly with respect to gives us 000 + 00 · 1 + 200 + 3(2000 + 00 · 20) + 6[ · 2000 + (0)20] = 0. Now substitute 1 for , 0 for , −2 for 0, and 2 for 00. 000 + 2 + 4 + 3(0 + 0) + 6[0 + (−8)] = 0 ⇒ 000 = −2 − 4 + 48 = 42. 41. (a) There are eight points with horizontal tangents: four at ≈ 157735 and four at ≈ 042265. (b) 0 = 32 − 6 + 2 2(23 − 32 − + 1) ⇒ 0 = −1 at (0 1) and 0 = 1 3 at (0 2). Equations of the tangent lines are = − + 1 and = 1 3 + 2. (c) 0 = 0 ⇒ 32 − 6 + 2 = 0 ⇒ = 1 ± 1 3√3 (d) By multiplying the right side of the equation by − 3, we obtain the first graph. By modifying the equation in other ways, we can generate the other graphs. (2 − 1)( − 2) = ( − 1)( − 2)( − 3) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.5 IMPLICIT DIFFERENTIATION ¤ 217 (2 − 4)( − 2) = ( − 1)( − 2) ( + 1)(2 − 1)( − 2) = ( − 1)( − 2) ( + 1)(2 − 1)( − 2) = ( − 1)( − 2) ( + 1)(2 − 1)( − 2) = ( − 1)( − 2) (2 + 1)( − 2) = (2 − 1)( − 2) ( + 1)(2 − 2) = ( − 1)(2 − 2) 42. (a) (b) (23 + 2 − 5) = (4 − 23 + 2) ⇒ 620 + 2 0 − 540 = 43 − 62 + 2 ⇒ 0 = 2(22 − 3 + 1) 62 + 2 − 54 = 2(2 − 1)( − 1) (6 + 2 − 53) . From the graph and the values for which 0 = 0, we speculate that there are 9 points with horizontal tangents: 3 at = 0, 3 at = 1 2, and 3 at = 1. The three horizontal tangents along the top of the wagon are hard to find, but by limiting the -range of the graph (to [16 17], for example) they are distinguishable. 43. From Exercise 31, a tangent to the lemniscate will be horizontal if 0 = 0 ⇒ 25 − 4(2 + 2) = 0 ⇒ [25 − 4(2 + 2)] = 0 ⇒ 2 + 2 = 25 4 (1). (Note that when is 0, is also 0, and there is no horizontal tangent at the origin.) Substituting 25 4 for 2 + 2 in the equation of the lemniscate, 2(2 + 2)2 = 25(2 − 2), we get 2 − 2 = 25 8 (2). Solving (1) and (2), we have 2 = 75 16 and 2 = 25 16, so the four points are ± 5√4 3 ± 5 4. 44. 2 2 + 2 2 = 1 ⇒ 22 + 2 2 0 = 0 ⇒ 0 = −22 ⇒ an equation of the tangent line at (0 0) is − 0 = −20 20 ( − 0). Multiplying both sides by 20 gives 02 − 202 = −02 + 22 0 . Since (0 0) lies on the ellipse, we have 0 2 + 0 2 = 2 0 2 + 02 2 = 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.218 ¤ CHAPTER 3 DIFFERENTIATION RULES 45. 2 2 − 2 2 = 1 ⇒ 22 − 2 2 0 = 0 ⇒ 0 = 22 ⇒ an equation of the tangent line at (0 0) is − 0 = 20 20 ( − 0). Multiplying both sides by 20 gives 02 − 202 = 02 − 22 0 . Since (0 0) lies on the hyperbola, we have 0 2 − 0 2 = 2 0 2 − 02 2 = 1. 46. √ + = √ ⇒ 1 2 √ + 0 2 = 0 ⇒ 0 = − √ ⇒ an equation of the tangent line at (0 0) is − 0 = − 0 √0 ( − 0). Now = 0 ⇒ = 0 − 0 √0 (−0) = 0 + √0 0, so the -intercept is 0 + √0 0. And = 0 ⇒ −0 = − 0 √0 ( − 0) ⇒ − 0 = 0 √0 0 ⇒ = 0 + √0 0, so the -intercept is 0 + √0 0. The sum of the intercepts is 0 + √0 0 + 0 + √0 0 = 0 + 2 √0 0 + 0 = √0 + 0 2 = √ 2 = . 47. If the circle has radius , its equation is 2 + 2 = 2 ⇒ 2 + 20 = 0 ⇒ 0 = − , so the slope of the tangent line at (0 0) is −0 0 . The negative reciprocal of that slope is −1 −00 = 0 0 , which is the slope of , so the tangent line at is perpendicular to the radius . 48. = ⇒ −10 = −1 ⇒ 0 = −1 −1 = −1 = −1 = ()−1 49. = (tan−1 )2 ⇒ 0 = 2(tan−1 )1 · (tan−1 ) = 2 tan−1 · 1 +12 = 2 tan 1 +−12 50. = tan−1(2) ⇒ 0 = 1 1 + (2)2 · (2) = 1 +14 · 2 = 1 +24 51. = sin−1(2 + 1) ⇒ 0 = 1 − (21 + 1)2 · (2 + 1) = 1 − (421+ 4 + 1) · 2 = √−422 − 4 = √−12 − 52. () = arccos √ ⇒ 0() = −1 −1(√)2 √ = −√11− 1 2−12 = −2√ √11 − 53. () = sec−1(3) ⇒PR 0() = · 1 3(3)2 − 1 (3) + sec−1(3) · 1 = 3√(362−) 1 + sec−1(3) = √63− 1 + sec−1(3) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.5 IMPLICIT DIFFERENTIATION ¤ 219 54. = tan−1 − √2 + 1 ⇒ 0 = 1 1 + − √2 + 1 2 1 − √2+ 1 = 1 + 2 − 2 √12 + 1 + 2 + 1 √√2+ 1 2 + 1 − = √2 + 1 − 21 + 2 − √2 + 1 √2 + 1 = √2 + 1 − 2√2 + 1 (1 + 2) − (2 + 1) = √2 + 1 − 2(1 + 2)√2 + 1 − = 1 2(1 + 2) 55. () = cot−1() + cot−1(1) ⇒ 0() = − 1 1 + 2 − 1 1 + (1)2 · 1 = − 1 1 + 2 − 2 2 + 1 · −12 = −1 +1 2 + 2 1+ 1 = 0. Note that this makes sense because () = 2 for 0 and () = 3 2 for 0. 56. () = arcsin(1) ⇒ 0() = 1 −1(1)2 1 = 1 −1 12 −12 = −1 −1 12 √14 = − 1 √4 − 2 = − 1 2(2 − 1) = − 1 | | √2 − 1 57. = sin−1 + √1 − 2 ⇒ 0 = · √1 1− 2 + (sin−1 )(1) + 12(1 − 2)−12(−2) = √1 − 2 + sin−1 − √1 − 2 = sin−1 58. = cos−1(sin−1 ) ⇒ 0 = −1 − (sin 1 −1 )2 · sin−1 = −1 − (sin 1 −1 )2 · √11− 2 59. = arccos ++ cos cos ⇒ 0 = −1 − +1 + cos cos 2 ( + cos )(− sin ( +)−cos (+)2 cos )(− sin ) = 1 √2 + 2 cos2 − 2 − 2 cos2 (2 − 2) sin | + cos | = 1 √2 − 2 √1 − cos2 (2 − 2) sin | + cos | = √2 − 2 | + cos | sin |sin | But 0 ≤ ≤ , so |sin | = sin . Also 0 ⇒ cos ≥ − −, so + cos 0. Thus 0 = √2 − 2 + cos . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.220 ¤ CHAPTER 3 DIFFERENTIATION RULES 60. = arctan1 1 +− = arctan 11 + − 12 ⇒ 0 = 1 1 + 1 1 +− 2 · 1 + 1 − 12 = 1 + 11 − 1 + · 1 2 11 + − −12 · (1 + )(−(1 + 1) −)(1 2 − )(1) = 1 1 + 1 + + 1 − 1 + · 1 2 1 + 1 − 12 · (1 +−2)2 = 1 +2 · 12 · (1 + (1 − ))1 1 2 2 · (1 +−2)2 = −1 2(1 − )12(1 + )12 = −1 2 √1 − 2 61. () = √1 − 2 arcsin ⇒ 0() = √1 − 2 · √1 1− 2 + arcsin · 1 2 1 − 2−12 (−2) = 1 − √arcsin 1 − 2 Note that 0 = 0 where the graph of has a horizontal tangent. Also note that 0 is negative when is decreasing and 0 is positive when is increasing. 62. () = arctan(2 − ) ⇒ 0() = 1 1 + (2 − )2 · (2 − ) = 1 + ( 22−−1)2 Note that 0 = 0 where the graph of has a horizontal tangent. Also note that 0 is negative when is decreasing and 0 is positive when is increasing. 63. Let = cos−1 . Then cos = and 0 ≤ ≤ ⇒ − sin = 1 ⇒ = − 1 sin = − 1 1 − cos2 = − 1 √1 − 2 . [Note that sin ≥ 0 for 0 ≤ ≤ .] 64. (a) Let = sec−1 . Then sec = and ∈ 0 2 ∪ 32. Differentiate with respect to : sec tan = 1 ⇒ = 1 sec tan = 1 sec sec2 − 1 = 1 √2 − 1. Note that tan2 = sec2 − 1 ⇒ tan = sec2 − 1 since tan 0 when 0 2 or 32 . (b) = sec−1 ⇒ sec = ⇒ sec tan = 1 ⇒ = sec 1tan . Now tan2 = sec2 − 1 = 2 − 1, so tan = ±√2 − 1. For ∈ 0 2 , ≥ 1, so sec = = || and tan ≥ 0 ⇒ = 1 √2 − 1 = 1 || √2 − 1. For ∈ 2 , ≤ −1, so || = − and tan = −√2 − 1 ⇒ = 1 sec tan = 1 −√2 − 1 = 1 (−) √2 − 1 = 1 || √2 − 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.5 IMPLICIT DIFFERENTIATION ¤ 221 65. 2 + 2 = 2 is a circle with center and + = 0 is a line through [assume and are not both zero]. 2 + 2 = 2 ⇒ 2 + 20 = 0 ⇒ 0 = −, so the slope of the tangent line at 0 (0 0) is −00. The slope of the line 0 is 00, which is the negative reciprocal of −00. Hence, the curves are orthogonal, and the families of curves are orthogonal trajectories of each other. 66. The circles 2 + 2 = and 2 + 2 = intersect at the origin where the tangents are vertical and horizontal [assume and are both nonzero]. If (0 0) is the other point of intersection, then 2 0 + 02 = 0 (1) and 2 0 + 02 = 0 (2). Now 2 + 2 = ⇒ 2 + 20 = ⇒ 0 = − 2 2 and 2 + 2 = ⇒ 2 + 20 = 0 ⇒ 0 = 2 − 2 . Thus, the curves are orthogonal at (0 0) ⇔ − 20 20 = − − 20 20 ⇔ 20 − 42 0 = 402 − 20 ⇔ 0 + 0 = 2(2 0 + 02), which is true by (1) and (2). 67. = 2 ⇒ 0 = 2 and 2 + 22 = [assume 0] ⇒ 2 + 40 = 0 ⇒ 20 = − ⇒ 0 = − 2() = − 2(2) = − 1 2 , so the curves are orthogonal if 6= 0. If = 0, then the horizontal line = 2 = 0 intersects 2 + 22 = orthogonally at ±√ 0, since the ellipse 2 + 22 = has vertical tangents at those two points. 68. = 3 ⇒ 0 = 32 and 2 + 32 = [assume 0] ⇒ 2 + 60 = 0 ⇒ 30 = − ⇒ 0 = − 3() = − 3(3) = − 1 32 , so the curves are orthogonal if 6= 0. If = 0, then the horizontal line = 3 = 0 intesects 2 + 32 = orthogonally at ±√ 0, since the ellipse 2 + 32 = has vertical tangents at those two points. 69. Since 2 2, we are assured that there are four points of intersection. (1) 2 2 + 2 2 = 1 ⇒ 22 + 2 2 0 = 0 ⇒ 20 = −2 ⇒ 0 = 1 = − 2 2 . (2) 2 2 − 2 2 = 1 ⇒ 22 − 220 = 0 ⇒ 20 = 2 ⇒ 0 = 2 = 2 2 . Now 12 = − 2 2 · 2 2 = − 22 22 · 2 2 (3). Subtracting equations, (1) − (2), gives us 22 + 22 − 22 + 22 = 0 ⇒ °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.222 ¤ CHAPTER 3 DIFFERENTIATION RULES 2 2 + 2 2 = 2 2 − 2 2 ⇒ 22 + 22 22 = 22 − 22 22 ⇒ 2(2 + 2) 22 = 2(2 − 2) 22 (4). Since 2 − 2 = 2 + 2, we have 2 − 2 = 2 + 2. Thus, equation (4) becomes 2 22 = 2 22 ⇒ 2 2 = 22 22 , and substituting for 2 2 in equation (3) gives us 12 = −2222 · 2222 = −1. Hence, the ellipse and hyperbola are orthogonal trajectories. 70. = ( + )−1 ⇒ 0 = −( + )−2 and = ( + )13 ⇒ 0 = 1 3( + )−23, so the curves are othogonal if the product of the slopes is −1, that is, −1 ( + )2 · 3( + )23 = −1 ⇒ = 3( + )2( + )23 ⇒ = 312 2 [since 2 = ( + )−2 and 2 = 2( + )23] ⇒ = 312 ⇒ 3 = 3 ⇒ = √3 3. 71. (a) + 22 ( − ) = ⇒ − + 2 − 3 2 = ⇒ ( − + 2 −1 − 3 −2) = () ⇒ 0 + · 1 − − 2 −2 · 0 + 23 −3 · 0 = 0 ⇒ 0( − 2 −2 + 23 −3) = − ⇒ 0 = − − 2 −2 + 23 −3 or = 3( − ) 3 − 2 + 23 (b) Using the last expression for from part (a), we get = (10 L)3[(1 mole)(004267 Lmole) − 10 L] (25 atm)(10 L)3 − (1 mole)2(3592 L2- atm mole2)(10 L) + 2(1 mole)3(3592 L2- atm mole2)(004267 L mole) = −995733 L4 2464386541 L3- atm ≈ −404 L atm 72. (a) 2 + + 2 + 1 = 0 ⇒ 2 + 0 + · 1 + 20 + 0 = 0 ⇒ 0( + 2) = −2 − ⇒ 0 = −2 − + 2 (b) Plotting the curve in part (a) gives us an empty graph, that is, there are no points that satisfy the equation. If there were any points that satisfied the equation, then and would have opposite signs; otherwise, all the terms are positive and their sum can not equal 0. 2 + + 2 + 1 = 0 ⇒ 2 + 2 + 2 − + 1 = 0 ⇒ ( + )2 = − 1. The left side of the last equation is nonnegative, but the right side is at most −1, so that proves there are no points that satisfy the equation. Another solution: 2 + + 2 + 1 = 1 22 + + 1 22 + 1 22 + 1 22 + 1 = 1 2(2 + 2 + 2) + 1 2(2 + 2) + 1 = 12 ( + )2 + 1 2(2 + 2) + 1 ≥ 1 Another solution: Regarding 2 + + 2 + 1 = 0 as a quadratic in , the discriminant is 2 − 4(2 + 1) = −32 − 4. This is negative, so there are no real solutions. (c) The expression for 0 in part (a) is meaningless; that is, since the equation in part (a) has no solution, it does not implicitly define a function of , and therefore it is meaningless to consider 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.5 IMPLICIT DIFFERENTIATION ¤ 223 73. To find the points at which the ellipse 2 − + 2 = 3 crosses the -axis, let = 0 and solve for . = 0 ⇒ 2 − (0) + 02 = 3 ⇔ = ±√3. So the graph of the ellipse crosses the -axis at the points ±√3 0. Using implicit differentiation to find 0, we get 2 − 0 − + 20 = 0 ⇒ 0(2 − ) = − 2 ⇔ 0 = − 2 2 − . So 0 at √3 0 is 0 − 2 √3 2(0) − √3 = 2 and 0 at −√3 0 is 2(0) + 0 + 2 √√33 = 2. Thus, the tangent lines at these points are parallel. 74. (a) We use implicit differentiation to find 0 = − 2 2 − as in Exercise 73. The slope of the tangent line at (−1 1) is = 1 − 2(−1) 2(1) − (−1) = 3 3 = 1, so the slope of the normal line is − 1 = −1, and its equation is − 1 = −1( + 1) ⇔ = −. Substituting − for in the equation of the ellipse, we get 2 − (−) + (−)2 = 3 ⇒ 32 = 3 ⇔ = ±1. So the normal line must intersect the ellipse again at = 1, and since the equation of the line is = −, the other point of intersection must be (1 −1). (b) 75. 22 + = 2 ⇒ 2 · 20 + 2 · 2 + · 0 + · 1 = 0 ⇔ 0(22 + ) = −22 − ⇔ 0 = −22 + 22 + . So −22 22 ++ = −1 ⇔ 22 + = 22 + ⇔ (2 + 1) = (2 + 1) ⇔ (2 + 1) − (2 + 1) = 0 ⇔ (2 + 1)( − ) = 0 ⇔ = − 1 2 or = . But = − 1 2 ⇒ 22 + = 1 4 − 1 2 6= 2, so we must have = . Then 22 + = 2 ⇒ 4 + 2 = 2 ⇔ 4 + 2 − 2 = 0 ⇔ (2 + 2)(2 − 1) = 0. So 2 = −2, which is impossible, or 2 = 1 ⇔ = ±1. Since = , the points on the curve where the tangent line has a slope of −1 are (−1 −1) and (1 1). 76. 2 + 42 = 36 ⇒ 2 + 80 = 0 ⇒ 0 = − 4 . Let ( ) be a point on 2 + 42 = 36 whose tangent line passes through (12 3). The tangent line is then − 3 = − 4 ( − 12), so − 3 = −4 ( − 12). Multiplying both sides by 4 gives 42 − 12 = −2 + 12, so 42 + 2 = 12( + ). But 42 + 2 = 36, so 36 = 12( + ) ⇒ + = 3 ⇒ = 3 − . Substituting 3 − for into 2 + 42 = 36 gives 2 + 4(3 − )2 = 36 ⇔ 2 + 36 − 24 + 42 = 36 ⇔ 52 − 24 = 0 ⇔ (5 − 24) = 0, so = 0 or = 24 5 . If = 0, = 3 − 0 = 3, and if = 24 5 , = 3 − 24 5 = − 9 5. So the two points on the ellipse are (0 3) and 24 5 − 9 5. Using − 3 = − 4( − 12) with ( ) = (0 3) gives us the tangent line − 3 = 0 or = 3. With ( ) = 24 5 − 9 5, we have − 3 = − 4(24 −955)( − 12) ⇔ − 3 = 2 3( − 12) ⇔ = 2 3 − 5. A graph of the ellipse and the tangent lines confirms our results. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.224 ¤ CHAPTER 3 DIFFERENTIATION RULES 77. (a) If = −1(), then () = . Differentiating implicitly with respect to and remembering that is a function of , we get 0() = 1, so = 01() ⇒ −10() = 0(−11()). (b) (4) = 5 ⇒ −1(5) = 4. By part (a), −10(5) = 1 0(−1(5)) = 1 0(4) = 1 2 3 = 3 2. 78. (a) Assume . Since is an increasing function, , and hence, + + ; that is, () () So () = + is an increasing function and therefore one-to-one. (b) −1(1) = ⇔ () = 1, so we need to find such that () = 1. By inspection, we see that (0) = 0 + 0 = 1, so = 0, and hence, −1(1) = 0. (c) (−1)0(1) = 1 0(−1(1)) = 1 0(0) [by part (b)]. Now () = + ⇒ 0() = 1 + , so 0(0) = 1 + 0 = 2. Thus, (−1)0(1) = 1 2. 79. (a) = () and 00 + 0 + = 0 ⇒ 00() + 0() + () = 0. If = 0, we have 0 + 0(0) + 0 = 0, so 0(0) = 0. (b) Differentiating 00 + 0 + = 0 implicitly, we get 000 + 00 · 1 + 00 + 0 + · 1 = 0 ⇒ 000 + 200 + 0 + = 0, so 000() + 2 00() + 0() + () = 0. If = 0, we have 0 + 2 00(0) + 0 + 1 [(0) = 1 is given] = 0 ⇒ 200(0) = −1 ⇒ 00(0) = − 1 2. 80. 2 + 42 = 5 ⇒ 2 + 4(20) = 0 ⇒ 0 = − 4 . Now let be the height of the lamp, and let ( ) be the point of tangency of the line passing through the points (3 ) and (−5 0). This line has slope ( − 0)[3 − (−5)] = 1 8. But the slope of the tangent line through the point ( ) can be expressed as 0 = − 4, or as − 0 − (−5) = + 5 [since the line passes through (−5 0) and ( )], so − 4 = + 5 ⇔ 42 = −2 − 5 ⇔ 2 + 42 = −5. But 2 + 42 = 5 [since ( ) is on the ellipse], so 5 = −5 ⇔ = −1. Then 42 = −2 − 5 = −1 − 5(−1) = 4 ⇒ = 1, since the point is on the top half of the ellipse. So 8 = + 5 = 1 −1 + 5 = 1 4 ⇒ = 2. So the lamp is located 2 units above the -axis. LABORATORY PROJECT Families of Implicit Curves 1. (a) There appear to be nine points of intersection. The “inner four” near the origin are about (±02 −09) and (±03 −11). The “outer five” are about (20 −89), (−28 −88), (−75 −77), (−78 −47), and (−80 15). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.LABORATORY PROJECT FAMILIES OF IMPLICIT CURVES ¤ 225 (b) We see from the graphs with = 5 and = 10, and for other values of , that the curves change shape but the nine points of intersection are the same. 2. (a) If = 0, the graph is the unit circle. As increases, the graph looks more diamondlike and then more crosslike (see the graph for ≥ 0). For −1 0 (see the graph), there are four hyperboliclike branches as well as an ellipticlike curve bounded by || ≤ 1 and || ≤ 1 for values of close to 0. As gets closer to −1, the branches and the curve become more rectangular, approaching the lines || = 1 and || = 1. For = −1, we get the lines = ±1 and = ±1. As decreases, we get four test-tubelike curves (see the graph) that are bounded by || = 1 and || = 1, and get thinner as || gets larger. ≥ 0 −1 0 ≤ −1 (b) The curve for = −1 is described in part (a). When = −1, we get 2 + 2 − 22 = 1 ⇔ 0 = 22 − 2 − 2 + 1 ⇔ 0 = (2 − 1)(2 − 1) ⇔ = ±1 or = ±1, which algebraically proves that the graph consists of the stated lines. (c) (2 + 2 + 22) = (1) ⇒ 2 + 2 0 + (2 · 2 0 + 2 · 2) = 0 ⇒ 2 0 + 22 0 = −2 − 22 ⇒ 2(1 + 2)0 = −2(1 + 2) ⇒ 0 = −(1 + 2) (1 + 2). For = −1, 0 = −(1 − 2) (1 − 2) = − (1 + )(1 − ) (1 + )(1 − ), so 0 = 0 when = ±1 or = 0 (which leads to = ±1) and 0 is undefined when = ±1 or = 0 (which leads to = ±1). Since the graph consists of the lines = ±1 and = ±1, the slope at any point on the graph is undefined or 0, which is consistent with the expression found for 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.226 ¤ CHAPTER 3 DIFFERENTIATION RULES 3.6 Derivatives of Logarithmic Functions 1. The differentiation formula for logarithmic functions, (log ) = ln 1 , is simplest when = because ln = 1. 2. () = ln − ⇒ 0() = · 1 + (ln ) · 1 − 1 = 1 + ln − 1 = ln 3. () = sin(ln ) ⇒ 0() = cos(ln ) · ln = cos(ln ) · 1 = cos(ln ) 4. () = ln(sin2 ) = ln(sin )2 = 2 ln |sin | ⇒ 0() = 2 · 1 sin · cos = 2 cot 5. () = ln 1 ⇒ 0() = 1 1 1 = −12 = −1 . Another solution: () = ln 1 = ln 1 − ln = − ln ⇒ 0() = −1 . 6. = 1 ln = (ln )−1 ⇒ 0 = −1(ln )−2 · 1 = (ln −1)2 7. () = log10 (1 + cos ) ⇒ 0() = 1 (1 + cos ) ln 10 (1 + cos ) = (1 + cos − sin) ln 10 8. () = log10 √ ⇒ 0() = √ 1ln 10 √ = √ 1ln 10 2√1 = 2(ln 10) 1 Or: () = log10 √ = log10 12 = 1 2 log10 ⇒ 0() = 1 2 1 ln 10 = 1 2 (ln 10) 9. () = ln(−2) = ln + ln −2 = ln − 2 ⇒ 0() = 1 − 2 10. () = √1 + ln ⇒ 0() = 1 2(1 + ln )−12 (1 + ln ) = 2√1 + ln 1 · 1 = 2√1 + ln 1 11. () = (ln )2 sin ⇒ 0() = (ln )2 cos + sin · 2 ln · 1 = ln ln cos + 2 sin 12. () = ln + √2 − 1 ⇒ 0() = 1 + √2 − 1 1 + √2− 1 = + √12 − 1 · √√2−2 −1 +1 = √21− 1 13. () = ln (2 + 1) 2 + 15 = ln(2 + 1)5 − ln(2 + 1)12 = 5 ln(2 + 1) − 1 2 ln(2 + 1) ⇒ 0() = 5 · 1 2 + 1 · 2 − 1 2 · 1 2 + 1 · 2 = 210 + 1 − 2 + 1 or (28+ 1)( 2 − + 10 2 + 1) 14. () = ln 1 − ⇒ 0() = (1 − )(1) − (ln )(−1) (1 − )2 · = 1 − + ln (1 − )2 15. () = ln ln ⇒ 0() = 1 ln ln = ln1 · 1 = ln 1 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.6 DERIVATIVES OF LOGARITHMIC FUNCTIONS ¤ 227 16. = ln 1 + − 3 ⇒ 0 = 1 1 + − 3 (1 + − 3) = 1 + 1 − 3−23 17. () = 2 log2 ⇒ 0() = 2 1 ln 2 + log2 · 2 ln 2 = 2 ln 2 1 + log2 (ln 2). Note that log2 (ln 2) = ln ln 2 (ln 2) = ln by the change of base theorem. Thus, 0() = 2 ln 2 1 + ln . 18. = ln(csc − cot ) ⇒ 0 = 1 csc − cot (csc − cot ) = csc −1 cot (− csc cot + csc2 ) = csccsc (csc − cot − cot ) = csc 19. = ln(− + −) = ln(−(1 + )) = ln(−) + ln(1 + ) = − + ln(1 + ) ⇒ 0 = −1 + 1 1 + = −1 − + 1 1 + = − 1 + 20. () = ln 2 2 − + 2 2 = ln 2 2 − + 2 2 12 = 12 ln 2 2 − + 2 2 = 1 2 ln(2 − 2) − 1 2 ln(2 + 2) ⇒ 0() = 1 2 · 1 2 − 2 · (−2) − 21 · 2 +1 2 · (2) = 2 − 2 − 2 + 2 = ((22+−2)2− )(2(+2 −2)2) = 3 + 2 − 3 + 2 (2 − 2)(2 + 2) = 22 4 − 4 21. = tan [ln( + )] ⇒ 0 = sec2[ln( + )] · 1 + · = sec2[ln( + )] + 22. = log2( log5 ) ⇒ 0 = 1 ( log5 )(ln 2) ( log5 ) = ( log51)(ln 2) · ln 5 1 + log5 = ( log5 )(ln 5)(ln 2) 1 + (ln 2) 1 . Note that log5 (ln 5) = ln ln 5 (ln 5) = ln by the change of base theorem. Thus, 0 = ln 1 ln 2 + ln 2 1 = 1 + ln ln ln 2 . 23. = √ ln ⇒ 0 = √ · 1 + (ln ) 1 2√ = 2 + ln 2√ ⇒ 00 = 2√ (1) − (2 + ln )(1√ ) (2√ )2 = 2√ − (2 + ln )(1√ ) 4 = 2 − (2 + ln ) √(4) = − ln 4√ 24. = ln 1 + ln ⇒ 0 = (1 + ln )(1 (1 + ln ) −)(ln 2 )(1) = (1 + ln 1 )2 ⇒ 00 = − [(1 + ln )2] [(1 + ln )2]2 [Reciprocal Rule] = − · 2(1 + ln2)(1 + ln · (1) + (1 + ln )4 )2 = − (1 + ln )[2 + (1 + ln )] 2(1 + ln )4 = − 3 + ln 2(1 + ln )3 25. = ln|sec | ⇒ 0 = 1 sec sec = 1 sec sec tan = tan ⇒ 00 = sec2 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.228 ¤ CHAPTER 3 DIFFERENTIATION RULES 26. = ln(1 + ln ) ⇒ 0 = 1 1 + ln · 1 = 1 (1 + ln ) ⇒ 00 = − [(1 + ln)] [(1 + ln )]2 [Reciprocal Rule] = −(1) + (1 + ln 2(1 + ln )2)(1) = −1 + 1 + ln 2(1 + ln )2 = −2(1 + ln 2 + ln )2 27. () = 1 − ln( − 1) ⇒ 0() = [1 − ln( − 1)] · 1 − · −1 − 1 [1 − ln( − 1)]2 = ( − 1)[1 − ln( − 1)] + − 1 [1 − ln( − 1)]2 = − 1 − ( − 1) ln( − 1) + ( − 1)[1 − ln( − 1)]2 = 2 − 1 − ( − 1) ln( − 1) ( − 1)[1 − ln( − 1)]2 Dom() = { | − 1 0 and 1 − ln( − 1) 6= 0} = { | 1 and ln( − 1) 6= 1} = | 1 and − 1 6= 1 = { | 1 and 6= 1 + } = (1 1 + ) ∪ (1 + ∞) 28. () = √2 + ln = (2 + ln )12 ⇒ 0() = 1 2 (2 + ln )−12 · 1 = 1 2√2 + ln Dom() = { | 2 + ln ≥ 0} = { | ln ≥ −2} = { | ≥ −2} = [−2 ∞). 29. () = ln(2 − 2) ⇒ 0() = 1 2 − 2(2 − 2) = 2(( −− 1) 2). Dom() = { | ( − 2) 0} = (−∞ 0) ∪ (2 ∞). 30. () = ln ln ln ⇒ 0() = 1 ln ln · 1 ln · 1 . Dom() = { | ln ln 0} = { | ln 1} = { | } = ( ∞). 31. () = ln( + ln ) ⇒ 0() = 1 + ln ( + ln ) = + ln 1 1 + 1 . Substitute 1 for to get 0(1) = 1 1 + ln 1 1 + 11 = 1 + 0 1 (1 + 1) = 1 · 2 = 2. 32. () = cos(ln 2) ⇒ 0() = − sin(ln 2) ln 2 = − sin(ln 2)12 (2) = −2 sin(ln 2). Substitute 1 for to get 0(1) = −2 sin(ln 12) 1 = −2 sin 0 = 0. 33. = ln(2 − 3 + 1) ⇒ 0 = 1 2 − 3 + 1 · (2 − 3) ⇒ 0(3) = 1 1 · 3 = 3, so an equation of a tangent line at (3 0) is − 0 = 3( − 3), or = 3 − 9. 34. = 2 ln ⇒ 0 = 2 · 1 + (ln )(2) ⇒ 0(1) = 1 + 0 = 1 , so an equation of a tangent line at (1 0) is − 0 = 1( − 1), or = − 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.6 DERIVATIVES OF LOGARITHMIC FUNCTIONS ¤ 229 35. () = sin + ln ⇒ 0() = cos + 1. This is reasonable, because the graph shows that increases when 0 is positive, and 0() = 0 when has a horizontal tangent. 36. = ln ⇒ 0 = (1) − ln 2 = 1 − ln 2 . 0(1) = 1 − 0 12 = 1 and 0() = 1 −2 1 = 0 ⇒ equations of tangent lines are − 0 = 1( − 1) or = − 1 and − 1 = 0( − ) or = 1. 37. () = + ln(cos ) ⇒ 0() = + 1 cos · (− sin ) = − tan . 0( 4 ) = 6 ⇒ − tan 4 = 6 ⇒ − 1 = 6 ⇒ = 7. 38. () = log(32 − 2) ⇒ 0() = 1 (32 − 2) ln · 6. 0(1) = 3 ⇒ 1 ln · 6 = 3 ⇒ 2 = ln ⇒ = 2. 39. = (2 + 2)2(4 + 4)4 ⇒ ln = ln[(2 + 2)2(4 + 4)4] ⇒ ln = 2 ln(2 + 2) + 4 ln(4 + 4) ⇒ 1 0 = 2 · 1 2 + 2 · 2 + 4 · 4 1+ 4 · 43 ⇒ 0 = 24+ 2 + 16 4 + 4 3 ⇒ 0 = (2 + 2)2(4 + 4)424+ 2 + 16 4 + 4 3 40. = − cos2 2 + + 1 ⇒ ln = ln 2−+cos + 1 2 ⇒ ln = ln − + ln | cos |2 − ln(2 + + 1) = − + 2 ln | cos | − ln(2 + + 1) ⇒ 1 0 = −1 + 2 · 1 cos (− sin ) − 1 2 + + 1(2 + 1) ⇒ 0 = −1 − 2 tan − 22+ + 1 + 1 ⇒ 0 = − − cos2 2 + + 1 1 + 2 tan + 22+ + 1 + 1 41. = 4−+ 1 1 ⇒ ln = ln4−+ 1 1 12 ⇒ ln = 1 2 ln( − 1) − 1 2 ln(4 + 1) ⇒ 1 0 = 1 2 1 − 1 − 1 2 1 4 + 1 · 43 ⇒ 0 = 2(1− 1) − 42+ 1 3 ⇒ 0 = 4−+ 1 1 21− 2 − 42+ 1 3 42. = √ 2−( + 1)23 ⇒ ln = ln122−( + 1)23 ⇒ ln = 1 2 ln + (2 − ) + 2 3 ln( + 1) ⇒ 1 0 = 1 2 · 1 + 2 − 1 + 2 3 · 1 + 1 ⇒ 0 = 21 + 2 − 1 + 32+ 3 ⇒ 0 = √ 2−( + 1)23 21 + 2 − 1 + 32+ 3 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.230 ¤ CHAPTER 3 DIFFERENTIATION RULES 43. = ⇒ ln = ln ⇒ ln = ln ⇒ 0 = (1) + (ln) · 1 ⇒ 0 = (1 + ln ) ⇒ 0 = (1 + ln ) 44. = cos ⇒ ln = ln cos ⇒ ln = cos ln ⇒ 1 0 = cos · 1 + ln · (− sin) ⇒ 0 = cos − ln sin ⇒ 0 = cos cos − ln sin 45. = sin ⇒ ln = ln sin ⇒ ln = sin ln ⇒ 0 = (sin ) · 1 + (ln )(cos ) ⇒ 0 = sin + ln cos ⇒ 0 = sin sin + ln cos 46. = √ ⇒ ln = ln √ ⇒ ln = ln 12 ⇒ ln = 1 2 ln ⇒ 1 0 = 1 2 · 1 + ln · 1 2 ⇒ 0 = 1 2 + 1 2 ln ⇒ 0 = 1 2√ (1 + ln ) 47. = (cos ) ⇒ ln = ln(cos ) ⇒ ln = ln cos ⇒ 1 0 = · 1 cos · (− sin ) + ln cos · 1 ⇒ 0 = ln cos − cos sin ⇒ 0 = (cos )(ln cos − tan ) 48. = (sin )ln ⇒ ln = ln(sin )ln ⇒ ln = ln · ln sin ⇒ 1 0 = ln · 1 sin · cos + ln sin · 1 ⇒ 0 = ln · cos sin + ln sin ⇒ 0 = (sin )ln ln cot + ln sin 49. = (tan )1 ⇒ ln = ln(tan )1 ⇒ ln = 1 ln tan ⇒ 1 0 = 1 · 1 tan · sec2 + ln tan · −12 ⇒ 0 = sec tan 2 − ln tan 2 ⇒ 0 = (tan )1 sec tan 2 − ln tan 2 or 0 = (tan )1 · 1csc sec − ln tan 50. = (ln )cos ⇒ ln = cos ln(ln ) ⇒ 0 = cos · 1 ln · 1 + (ln ln )(− sin ) ⇒ 0 = (ln )cos cos ln − sin ln ln 51. = ln(2 + 2) ⇒ 0 = 1 2 + 2 (2 + 2) ⇒ 0 = 22+ 2 + 2 0 ⇒ 20 + 20 = 2 + 20 ⇒ 20 + 20 − 20 = 2 ⇒ (2 + 2 − 2)0 = 2 ⇒ 0 = 2 2 + 2 − 2 52. = ⇒ ln = ln ⇒ · 1 + (ln ) · 0 = · 1 · 0 + ln ⇒ 0 ln − 0 = ln − ⇒ 0 = ln − ln − °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.7 RATES OF CHANGE IN THE NATURAL AND SOCIAL SCIENCES ¤ 231 53. () = ln( − 1) ⇒ 0() = 1 ( − 1) = ( − 1)−1 ⇒ 00() = −( − 1)−2 ⇒ 000 () = 2( − 1)−3 ⇒ (4)() = −2 · 3( − 1)−4 ⇒ · · · ⇒ ()() = (−1)−1 · 2 · 3 · 4 · · · · · ( − 1)( − 1)− = (−1)−1 ( − 1)! ( − 1) 54. = 8 ln , so 9 = 80 = 8(87 ln + 7). But the eighth derivative of 7 is 0, so we now have 8(87 ln ) = 7(8 · 76 ln + 86) = 7(8 · 76 ln ) = 6(8 · 7 · 65 ln ) = · · · = (8! 0 ln ) = 8! 55. If () = ln (1 + ), then 0() = 1 1 + , so 0(0) = 1. Thus, lim →0 ln(1 + ) = lim →0 () = lim →0 () − (0) − 0 = 0(0) = 1. 56. Let = . Then = , and as → ∞, → ∞. Therefore, lim →∞ 1 + = lim →∞ 1 + 1 = lim →∞ 1 + 1 = by Equation 6. 3.7 Rates of Change in the Natural and Social Sciences 1. (a) = () = 3 − 82 + 24 (in feet) ⇒ () = 0() = 32 − 16 + 24 (in fts) (b) (1) = 3(1)2 − 16(1) + 24 = 11 fts (c) The particle is at rest when () = 0. 32 − 16 + 24 = 0 ⇒ −(−16) ± (−16)2 − 4(3)(24) 2(3) = 16 ± √−32 6 . The negative discriminant indicates that is never 0 and that the particle never rests. (d) From parts (b) and (c), we see that () 0 for all , so the particle is always moving in the positive direction. (e) The total distance traveled during the first 6 seconds (since the particle doesn’t change direction) is (6) − (0) = 72 − 0 = 72 ft. (f ) (g) () = 32 − 16 + 24 ⇒ () = 0() = 6 − 16 (in (fts)s or fts2). (1) = 6(1) − 16 = −10 fts2 (h) (i) The particle is speeding up when and have the same sign. is always positive and is positive when 6 − 16 0 ⇒ 8 3, so the particle is speeding up when 8 3. It is slowing down when and have opposite signs; that is, when 0 ≤ 8 3. 2. (a) = () = 9 2 + 9 (in feet) ⇒ () = 0() = (2 + 9)(9) (2 + 9) −29(2) = −(922+ 9) + 81 2 = −(9( 2+ 9) 2 − 9) 2 (in fts) (b) (1) = −9(1 − 9) (1 + 9)2 = 72 100 = 072 fts °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.232 ¤ CHAPTER 3 DIFFERENTIATION RULES (c) The particle is at rest when () = 0. −9(2 − 9) (2 + 9)2 = 0 ⇔ 2 − 9 = 0 ⇒ = 3 s [since ≥ 0]. (d) The particle is moving in the positive direction when () 0. −9(2 − 9) (2 + 9)2 0 ⇒ −9(2 − 9) 0 ⇒ 2 − 9 0 ⇒ 2 9 ⇒ 0 ≤ 3. (e) Since the particle is moving in the positve direction and in the negative direction, we need to calculate the distance traveled in the intervals [0 3] and[3 6], respectively. |(3) − (0)| = 27 18 − 0 = 3 2 |(6) − (3)| = 54 45 − 27 18 = 10 3 The total distance is 3 2 + 10 3 = 9 5 or 18 ft. (f ) (g) () = −9 2 − 9 (2 + 9)2 ⇒ () = 0() = −9 (2 + 9)2(2) − (2 − 9)2(2 + 9)(2) [(2 + 9)2]2 = −9 2(2 + 9)[((22+ 9) + 9)4− 2(2 − 9)] = 18((22+ 9) − 27) 3 . (1) = 18(−26) 103 = −0468 fts2 (h) (i) The particle is speeding up when and have the same sign. is negative for 0 √27 [≈ 52], so from the figure in part (h), we see that and are both negative for 3 3√3. The particle is slowing down when and have opposite signs. This occurs when 0 3 and when 3√3. 3. (a) = () = sin(2) (in feet) ⇒ () = 0() = cos(2) · (2) = 2 cos(2) (in fts) (b) (1) = 2 cos 2 = 2 (0) = 0 fts (c) The particle is at rest when () = 0. 2 cos 2 = 0 ⇔ cos 2 = 0 ⇔ 2 = 2 + ⇔ = 1 + 2, where is a nonnegative integer since ≥ 0. (d) The particle is moving in the positive direction when () 0. From part (c), we see that changes sign at every positive odd integer. is positive when 0 1, 3 5, 7 9, and so on. (e) changes sign at = 1, 3, and 5 in the interval [0 6]. The total distance traveled during the first 6 seconds is |(1) − (0)| + |(3) − (1)| + |(5) − (3)| + |(6) − (5)| = |1 − 0| + |−1 − 1| + |1 − (−1)| + |0 − 1| = 1 + 2 + 2 + 1 = 6 ft °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.7 RATES OF CHANGE IN THE NATURAL AND SOCIAL SCIENCES ¤ 233 (f ) (g) () = 2 cos(2) ⇒ () = 0() = 2 [− sin(2) · (2)] = (−24) sin(2) fts2 (1) = (−24) sin(2) = −24 fts2 (h) (i) The particle is speeding up when and have the same sign. From the figure in part (h), we see that and are both positive when 3 4 and both negative when 1 2 and 5 6. Thus, the particle is speeding up when 1 2, 3 4, and 5 6. The particle is slowing down when and have opposite signs; that is, when 0 1, 2 3, and 4 5. 4. (a) = () = 2− (in feet) ⇒ () = 0() = 2(−−) + −(2) = −(− + 2) (in fts) (b) (1) = (1)−1(−1 + 2) = 1 fts (c) The particle is at rest when () = 0. () = 0 ⇔ = 0 or 2 s. (d) The particle is moving in the positive direction when () 0 ⇔ −(− + 2) 0 ⇔ (− + 2) 0 ⇔ 0 2. (e) changes sign at = 2 in the interval [0 6]. The total distance traveled during the first 6 seconds is |(2) − (0)| + |(6) − (2)| = 4−2 − 0 + 36−6 − 4−2 = 4−2 + 4−2 − 36−6 = 8−2 − 36−6 ≈ 099 ft (f ) (g) () = (2 − 2)− ⇒ () = 0() = (2 − 2)(−−) + −(2 − 2) = − −(2 − 2) + (2 − 2) = −(2 − 4 + 2) fts2 (1) = −1(1 − 4 + 2) = −1 fts2 (h) (i) () = 0 ⇔ 2 − 4 + 2 = 0 [− 6= 0] ⇔ = 4 ± √8 2 = 2 ± √2 [≈ 06 and 34]. The particle is speeding up when and have the same sign. Using the previous information and the figure in part (h), we see that and are both positive when 0 2 − √2 and both negative when 2 2 + √2. The particle is slowing down when and have opposite signs. This occurs when 2 − √2 2 and 2 + √2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.234 ¤ CHAPTER 3 DIFFERENTIATION RULES 5. (a) From the figure, the velocity is positive on the interval (0 2) and negative on the interval (2 3). The acceleration is positive (negative) when the slope of the tangent line is positive (negative), so the acceleration is positive on the interval (0 1), and negative on the interval (1 3). The particle is speeding up when and have the same sign, that is, on the interval (0 1) when 0 and 0, and on the interval (2 3) when 0 and 0. The particle is slowing down when and have opposite signs, that is, on the interval (1 2) when 0 and 0. (b) 0 on (0 3) and 0 on (3 4). 0 on (1 2) and 0 on (0 1) and (2 4). The particle is speeding up on (1 2) [ 0, 0] and on (3 4) [ 0, 0]. The particle is slowing down on (0 1) and (2 3) [ 0, 0]. 6. (a) The velocity is positive when is increasing, that is, on the intervals (0 1) and (3 4); and it is negative when is decreasing, that is, on the interval (1 3). The acceleration is positive when the graph of is concave upward ( is increasing), that is, on the interval (2 4); and it is negative when the graph of is concave downward ( is decreasing), that is, on the interval (0 2). The particle is speeding up on the interval (1 2) [ 0, 0] and on (3 4) [ 0, 0]. The particle is slowing down on the interval (0 1) [ 0, 0] and on (2 3) [ 0, 0]. (b) The velocity is positive on (3 4) and negative on (0 3). The acceleration is positive on (0 1) and (2 4) and negative on (1 2). The particle is speeding up on the interval (1 2) [ 0, 0] and on (3 4) [ 0, 0]. The particle is slowing down on the interval (0 1) [ 0, 0] and on (2 3) [ 0, 0]. 7. (a) () = 2 + 245 − 492 ⇒ () = 0() = 245 − 98. The velocity after 2 s is (2) = 245 − 98(2) = 49 ms and after 4 s is (4) = 245 − 98(4) = −147 ms. (b) The projectile reaches its maximum height when the velocity is zero. () = 0 ⇔ 245 − 98 = 0 ⇔ = 245 98 = 25 s. (c) The maximum height occurs when = 25. (25) = 2 + 245(25) − 49(25)2 = 32625 m or 32 5 8 m. (d) The projectile hits the ground when = 0 ⇔ 2 + 245 − 492 = 0 ⇔ = −245 ± 2452 − 4(−49)(2) 2(−49) ⇒ = ≈ 508 s [since ≥ 0] (e) The projectile hits the ground when = . Its velocity is () = 245 − 98 ≈ −253 ms [downward]. 8. (a) At maximum height the velocity of the ball is 0 fts. () = 0() = 80 − 32 = 0 ⇔ 32 = 80 ⇔ = 5 2. So the maximum height is 5 2 = 80 5 2 − 16 5 22 = 200 − 100 = 100 ft. (b) () = 80 − 162 = 96 ⇔ 162 − 80 + 96 = 0 ⇔ 16(2 − 5 + 6) = 0 ⇔ 16( − 3)( − 2) = 0. So the ball has a height of 96 ft on the way up at = 2 and on the way down at = 3. At these times the velocities are (2) = 80 − 32(2) = 16 fts and (3) = 80 − 32(3) = −16 fts, respectively. 9. (a) () = 15 − 1862 ⇒ () = 0() = 15 − 372. The velocity after 2 s is (2) = 15 − 372(2) = 756 ms. (b) 25 = ⇔ 1862 − 15 + 25 = 0 ⇔ = 15 ± 152 − 4(186)(25) 2(186) ⇔ = 1 ≈ 235 or = 2 ≈ 571. The velocities are (1) = 15 − 3721 ≈ 624 ms [upward] and (2) = 15 − 3722 ≈ −624 ms [downward]. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.7 RATES OF CHANGE IN THE NATURAL AND SOCIAL SCIENCES ¤ 235 10. (a) () = 4 − 43 − 202 + 20 ⇒ () = 0() = 43 − 122 − 40 + 20. = 20 ⇔ 43 − 122 − 40 + 20 = 20 ⇔ 43 − 122 − 40 = 0 ⇔ 4(2 − 3 − 10) = 0 ⇔ 4( − 5)( + 2) = 0 ⇔ = 0 s or 5 s [for ≥ 0]. (b) () = 0() = 122 − 24 − 40. = 0 ⇔ 122 − 24 − 40 = 0 ⇔ 4(32 − 6 − 10) = 0 ⇔ = 6 ± 62 − 4(3)(−10) 2(3) = 1 ± 1 3√39 ≈ 308 s [for ≥ 0]. At this time, the acceleration changes from negative to positive and the velocity attains its minimum value. 11. (a) () = 2 ⇒ 0() = 2. 0(15) = 30 mm2mm is the rate at which the area is increasing with respect to the side length as reaches 15 mm. (b) The perimeter is () = 4, so 0() = 2 = 1 2(4) = 1 2(). The figure suggests that if ∆ is small, then the change in the area of the square is approximately half of its perimeter (2 of the 4 sides) times ∆. From the figure, ∆ = 2 (∆) + (∆)2. If ∆ is small, then ∆ ≈ 2 (∆) and so ∆∆ ≈ 2. 12. (a) () = 3 ⇒ = 32. =3 = 3(3)2 = 27 mm3mm is the rate at which the volume is increasing as increases past 3 mm. (b) The surface area is () = 62, so 0() = 32 = 1 2(62) = 1 2(). The figure suggests that if ∆ is small, then the change in the volume of the cube is approximately half of its surface area (the area of 3 of the 6 faces) times ∆. From the figure, ∆ = 32(∆) + 3(∆)2 + (∆)3. If ∆ is small, then ∆ ≈ 32(∆) and so ∆∆ ≈ 32. 13. (a) Using () = 2, we find that the average rate of change is: (i) (3) − (2) 3 − 2 = 9 − 4 1 = 5 (ii) (25) − (2) 25 − 2 = 625 − 4 05 = 45 (iii) (21) − (2) 21 − 2 = 441 − 4 01 = 41 (b) () = 2 ⇒ 0() = 2, so 0(2) = 4. (c) The circumference is () = 2 = 0(). The figure suggests that if ∆ is small, then the change in the area of the circle (a ring around the outside) is approximately equal to its circumference times ∆. Straightening out this ring gives us a shape that is approximately rectangular with length 2 and width ∆, so ∆ ≈ 2(∆). Algebraically, ∆ = ( + ∆) − () = ( + ∆)2 − 2 = 2(∆) + (∆)2. So we see that if ∆ is small, then ∆ ≈ 2(∆) and therefore, ∆∆ ≈ 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.236 ¤ CHAPTER 3 DIFFERENTIATION RULES 14. After seconds the radius is = 60, so the area is () = (60)2 = 36002 ⇒ 0() = 7200 ⇒ (a) 0(1) = 7200 cm2s (b) 0(3) = 21 600 cm2s (c) 0(5) = 36,000 cm2s As time goes by, the area grows at an increasing rate. In fact, the rate of change is linear with respect to time. 15. () = 42 ⇒ 0() = 8 ⇒ (a) 0(1) = 8 ft2ft (b) 0(2) = 16 ft2ft (c) 0(3) = 24 ft2ft As the radius increases, the surface area grows at an increasing rate. In fact, the rate of change is linear with respect to the radius. 16. (a) Using () = 4 33, we find that the average rate of change is: (i) (8) − (5) 8 − 5 = 43 (512) − 4 3(125) 3 = 172 m3m (ii) (6) − (5) 6 − 5 = 43 (216) − 4 3(125) 1 = 1213 m3m (iii) (51) − (5) 51 − 5 = 43 (51)3 − 4 3(5)3 01 = 102013 m3m (b) 0() = 42, so 0(5) = 100 m3m. (c) () = 4 33 ⇒ 0() = 42 = (). By analogy with Exercise 13(c), we can say that the change in the volume of the spherical shell, ∆ , is approximately equal to its thickness, ∆, times the surface area of the inner sphere. Thus, ∆ ≈ 42(∆) and so ∆∆ ≈ 42. 17. The mass is () = 32, so the linear density at is () = 0() = 6. (a) (1) = 6 kgm (b) (2) = 12 kgm (c) (3) = 18 kgm Since is an increasing function, the density will be the highest at the right end of the rod and lowest at the left end. 18. () = 50001 − 40 1 2 ⇒ 0() = 5000 · 21 − 40 1 − 40 1 = −2501 − 40 1 (a) 0(5) = −2501 − 40 5 = −21875 galmin (b) 0(10) = −2501 − 10 40 = −1875 galmin (c) 0(20) = −2501 − 20 40 = −125 galmin (d) 0(40) = −2501 − 40 40 = 0 galmin The water is flowing out the fastest at the beginning— when = 0, 0() = −250 galmin. The water is flowing out the slowest at the end— when = 40, 0() = 0. As the tank empties, the water flows out more slowly. 19. The quantity of charge is () = 3 − 22 + 6 + 2, so the current is 0() = 32 − 4 + 6. (a) 0(05) = 3(05)2 − 4(05) + 6 = 475 A (b) 0(1) = 3(1)2 − 4(1) + 6 = 5 A The current is lowest when 0 has a minimum. 00() = 6 − 4 0 when 2 3. So the current decreases when 2 3 and increases when 2 3. Thus, the current is lowest at = 2 3 s. 20. (a) = 2 = ()−2 ⇒ = −2()−3 = −2 3 , which is the rate of change of the force with respect to the distance between the bodies. The minus sign indicates that as the distance between the bodies increases, the magnitude of the force exerted by the body of mass on the body of mass is decreasing. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.7 RATES OF CHANGE IN THE NATURAL AND SOCIAL SCIENCES ¤ 237 (b) Given 0(20,000) = −2, find 0(10,000). −2 = −2 20,0003 ⇒ = 20,0003. 0(10 000) = −2(20,0003) 10,0003 = −2 · 23 = −16 Nkm 21. With = 01 − 22 −12, = () = () + () = 01 − 22 −12 · + · 0−12 1 − 22 −32 −22 () = 01 − 22 −32 · 1 − 22 + 22 = (1 − 20 2)32 Note that we factored out (1 − 22)−32 since −32 was the lesser exponent. Also note that () = . 22. (a) () = 7 + 5 cos[0503( − 675)] ⇒ 0() = −5 sin[0503( − 675)](0503) = −2515 sin[0503( − 675)]. At 3:00 AM, = 3, and 0(3) = −2515 sin[0503(−375)] ≈ 239 mh (rising). (b) At 6:00 AM, = 6, and 0(6) = −2515 sin[0503(−075)] ≈ 093 mh (rising). (c) At 9:00 AM, = 9, and 0(9) = −2515 sin[0503(225)] ≈ −228 mh (falling). (d) At noon, = 12, and 0(12) = −2515 sin[0503(525)] ≈ −121 mh (falling). 23. (a) To find the rate of change of volume with respect to pressure, we first solve for in terms of . = ⇒ = ⇒ = − 2 . (b) From the formula for in part (a), we see that as increases, the absolute value of decreases. Thus, the volume is decreasing more rapidly at the beginning. (c) = − 1 = − 1 −2 = ( ) = = 1 24. (a) [C] = 2 + 1 ⇒ rate of reaction = [C] = ( + 1)( ( 2+ 1) ) − (22)() = 2(( + 1 + 1) −2) = ( 2+ 1) 2 (b) If = [C], then − = − 2 + 1 = 2 + − 2 + 1 = + 1. So ( − )2 = + 12 = ( 2+ 1) 2 = [C] [from part (a)] = . (c) As → ∞, [C] = 2 + 1 = (2) ( + 1) = 2 + (1) → 2 = molesL. (d) As → ∞, [C] = 2 ( + 1)2 → 0. (e) As increases, nearly all of the reactants A and B are converted into product C. In practical terms, the reaction virtually stops. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.238 ¤ CHAPTER 3 DIFFERENTIATION RULES 25. In Example 6, the population function was = 2 0. Since we are tripling instead of doubling and the initial population is 400, the population function is () = 400 · 3. The rate of growth is 0() = 400 · 3 · ln 3, so the rate of growth after 25 hours is 0(25) = 400 · 325 · ln 3 ≈ 6850 bacteriahour 26. = () = 1 + −07 ⇒ 0 = −(1 + · − 07−(0−70)27) [Reciprocal Rule]. When = 0, = 20 and 0 = 12. (0) = 20 ⇒ 20 = 1 + ⇒ = 20(1 + ). 0(0) = 12 ⇒ 12 = (1 + 07 )2 ⇒ 12 = 07(20)(1 + (1 + )2 ) ⇒ 12 14 = 1 + ⇒ 6(1 + ) = 7 ⇒ 6 + 6 = 7 ⇒ = 6 and = 20(1 + 6) = 140. For the long run, we let increase without bound. lim →∞ () = lim →∞ 140 1 + 6−07 = 140 1 + 6 · 0 = 140, indicating that the yeast population stabilizes at 140 cells. 27. (a) 1920: 1 = 1860 − 1750 1920 − 1910 = 110 10 = 11, 2 = 2070 − 1860 1930 − 1920 = 210 10 = 21, (1 + 2)/ 2 = (11 + 21)2 = 16 millionyear 1980: 1 = 4450 − 3710 1980 − 1970 = 740 10 = 74, 2 = 5280 − 4450 1990 − 1980 = 830 10 = 83, (1 + 2)/ 2 = (74 + 83)2 = 785 millionyear (b) () = 3 + 2 + + (in millions of people), where ≈ −0000 284 900 3, ≈ 0522 433 122 43, ≈ −6395 641 396, and ≈ 1720586 081. (c) () = 3 + 2 + + ⇒ 0() = 32 + 2 + (in millions of people per year) (d) 1920 corresponds to = 20 and 0(20) ≈ 1416 millionyear. 1980 corresponds to = 80 and 0(80) ≈ 7172 millionyear. These estimates are smaller than the estimates in part (a). (e) () = (where = 143653 × 109 and = 101395) ⇒ 0() = ln (in millions of people per year) (f ) 0(20) ≈ 2625 millionyear [much larger than the estimates in part (a) and (d)]. 0(80) ≈ 6028 millionyear [much smaller than the estimates in parts (a) and (d)]. (g) 0(85) ≈ 7624 millionyear and 0(85) ≈ 6461 millionyear. The first estimate is probably more accurate. 28. (a) () = 4 + 3 + 2 + + , where ≈ −1199 781 × 10−6, ≈ 9545 853 × 103, ≈ −28478 550, ≈ 37,757105 467, and ≈ −1877 031 × 107. (b) () = 4 + 3 + 2 + + ⇒ 0() = 43 + 32 + 2 + . (c) Part (b) gives 0(1990) ≈ 0106 years of age per year. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.7 RATES OF CHANGE IN THE NATURAL AND SOCIAL SCIENCES ¤ 239 (d) 29. (a) Using = 4(2 − 2) with = 001, = 3, = 3000, and = 0027, we have as a function of : () = 3000 4(0027)3(0012 − 2). (0) = 0925 cms, (0005) = 0694 cms, (001) = 0. (b) () = 4(2 − 2) ⇒ 0() = 4(−2) = −2 . When = 3, = 3000, and = 0027, we have 0() = − 3000 2(0027)3. 0(0) = 0, 0(0005) = −92592 (cms)cm, and 0(001) = −185185 (cms)cm. (c) The velocity is greatest where = 0 (at the center) and the velocity is changing most where = = 001 cm (at the edge). 30. (a) (i) = 1 2 = 12 −1 ⇒ = − 1 2 −2 = −21 2 (ii) = 1 2 = 21√ 12 ⇒ = 1221√ −12 = 4 √1 (iii) = 1 2 = √2 −12 ⇒ = −12 √2 −32 = −4 √32 (b) Note: Illustrating tangent lines on the generic figures may help to explain the results. (i) 0 and is decreasing ⇒ is increasing ⇒ higher note (ii) 0 and is increasing ⇒ is increasing ⇒ higher note (iii) 0 and is increasing ⇒ is decreasing ⇒ lower note °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.240 ¤ CHAPTER 3 DIFFERENTIATION RULES 31. (a) () = 2000 + 3 + 0012 + 000023 ⇒ 0() = 0 + 3(1) + 001(2) + 00002(32) = 3 + 002 + 000062 (b) 0(100) = 3 + 002(100) + 00006(100)2 = 3 + 2 + 6 = $11pair. 0(100) is the rate at which the cost is increasing as the 100th pair of jeans is produced. It predicts the (approximate) cost of the 101st pair. (c) The cost of manufacturing the 101st pair of jeans is (101) − (100) = 26110702 − 2600 = 110702 ≈ $1107. This is close to the marginal cost from part (b). 32. (a) () = 84 + 016 − 000062 + 00000033 ⇒ 0() = 016 − 00012 + 00000092, and 0(100) = 016 − 00012(100) + 0000009(100)2 = 013. This is the rate at which the cost is increasing as the 100th item is produced. (b) The actual cost of producing the 101st item is (101) − (100) = 9713030299 − 97 ≈ $013 33. (a) () = () ⇒ 0() = 0() − () · 1 2 = 0() − () 2 . 0() 0 ⇒ () is increasing; that is, the average productivity increases as the size of the workforce increases. (b) 0() is greater than the average productivity ⇒ 0() () ⇒ 0() () ⇒ 0() () ⇒ 0() − () 0 ⇒ 0() − () 2 0 ⇒ 0() 0. 34. (a) = = (1 + 404)(96−06) − (40 + 2404)(16−06) (1 + 404)2 = 96−06 + 384−02 − 64−06 − 384−02 (1 + 404)2 = − 544−06 (1 + 404)2 (b) At low levels of brightness, is quite large [(0) = 40] and is quickly decreasing, that is, is negative with large absolute value. This is to be expected: at low levels of brightness, the eye is more sensitive to slight changes than it is at higher levels of brightness. 35. = ln3 + √92 2 − 8 = ln3 + √9 2 − 8 − ln 2 ⇒ = 1 3 + √9 2 − 8 3 + √9 2 − 8 − 0 = 3 + 1 2(932+−√89)−21−2(18 8 − 8) = 3 + √992−−48 3 + √9 2 − 8 = 3√9 2 − 8 + 9 − 4 √9 2 − 8 3 + √9 2 − 8 . This derivative represents the rate of change of duration of dialysis required with respect to the initial urea concentration. 36. () = 2√ ⇒ 0() = 2 · 1 2()−12 · = √ = . 0() is the rate of change of the wave speed with respect to the reproductive rate. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.8 EXPONENTIAL GROWTH AND DECAY ¤ 241 37. = ⇒ = = (10)(00821) = 1 0821 ( ). Using the Product Rule, we have = 1 0821 [() 0() + () 0()] = 1 0821 [(8)(−015) + (10)(010)] ≈ −02436 Kmin. 38. (a) If = 0, the population is stable (it is constant). (b) = 0 ⇒ = 01 − ⇒ 0 = 1 − ⇒ = 1 − 0 ⇒ = 1 − 0 . If = 10,000, 0 = 5% = 005, and = 4% = 004, then = 10,0001 − 4 5 = 2000. (c) If = 005, then = 10,0001 − 5 5 = 0. There is no stable population. 39. (a) If the populations are stable, then the growth rates are neither positive nor negative; that is, = 0 and = 0. (b) “The caribou go extinct” means that the population is zero, or mathematically, = 0. (c) We have the equations = − and = − + . Let = = 0, = 005, = 0001, = 005, and = 00001 to obtain 005 − 0001 = 0 (1) and −005 + 00001 = 0 (2). Adding 10 times (2) to (1) eliminates the -terms and gives us 005 − 05 = 0 ⇒ = 10. Substituting = 10 into (1) results in 005(10) − 0001(10) = 0 ⇔ 05 − 001 2 = 0 ⇔ 50 − 2 = 0 ⇔ (50 − ) = 0 ⇔ = 0 or 50. Since = 10, = 0 or 500. Thus, the population pairs ( ) that lead to stable populations are (0 0) and (500 50). So it is possible for the two species to live in harmony. 3.8 Exponential Growth and Decay 1. The relative growth rate is 1 = 07944, so = 07944 and, by Theorem 2, () = (0)07944 = 207944. Thus, (6) = 207944(6) ≈ 23499 or about 235 members. 2. (a) By Theorem 2, () = (0) = 50. In 20 minutes 1 3 hour, there are 100 cells, so 1 3 = 503 = 100 ⇒ 3 = 2 ⇒ 3 = ln 2 ⇒ = 3 ln 2 = ln(23) = ln 8. (b) () = 50(ln 8) = 50 · 8 (c) (6) = 50 · 86 = 50 · 218 = 13,107,200 cells (d) = ⇒ 0(6) = (6) = (ln 8)(6) ≈ 27,255,656 cellsh (e) () = 106 ⇔ 50 · 8 = 1,000,000 ⇔ 8 = 20,000 ⇔ ln 8 = ln 20,000 ⇔ = ln 20,000 ln 8 ≈ 476 h 3. (a) By Theorem 2, () = (0) = 100. Now (1) = 100(1) = 420 ⇒ = 420 100 ⇒ = ln 42. So () = 100(ln 42) = 100(42). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.242 ¤ CHAPTER 3 DIFFERENTIATION RULES (b) (3) = 100(42)3 = 74088 ≈ 7409 bacteria (c) = ⇒ 0(3) = · (3) = (ln 42)100(42)3 [from part (a)] ≈ 10,632 bacteriah (d) () = 100(42) = 10,000 ⇒ (42) = 100 ⇒ = (ln 100)(ln 42) ≈ 32 hours 4. (a) () = (0) ⇒ (2) = (0)2 = 400 and (6) = (0)6 = 25,600. Dividing these equations, we get 62 = 25,600400 ⇒ 4 = 64 ⇒ 4 = ln 26 = 6 ln 2 ⇒ = 3 2 ln 2 ≈ 10397, about 104% per hour. (b) 400 = (0)2 ⇒ (0) = 4002 ⇒ (0) = 4003 ln 2 = 400 ln 23 = 40023 = 50. (c) () = (0) = 50(32)(ln 2) = 50(ln 2)(32) ⇒ () = 50(2)15 (d) (45) = 50(2)15(45) = 50(2)675 ≈ 5382 bacteria (e) = = 32 ln 2(50(2)675) ≈ 5596 bacteriah (f ) () = 50,000 ⇒ 50,000 = 50(2)15 ⇒ 1000 = (2)1.5 ⇒ ln 1000 = 1.5 ln 2 ⇒ = ln 1000 1.5 ln 2 ≈ 6.64 h 5. (a) Let the population (in millions) in the year be (). Since the initial time is the year 1750, we substitute − 1750 for in Theorem 2, so the exponential model gives () = (1750)(−1750). Then (1800) = 980 = 790(1800−1750) ⇒ 980 790 = (50) ⇒ ln 980 790 = 50 ⇒ = 50 1 ln 980 790 ≈ 00043104. So with this model, we have (1900) = 790(1900−1750) ≈ 1508 million, and (1950) = 790(1950−1750) ≈ 1871 million. Both of these estimates are much too low. (b) In this case, the exponential model gives () = (1850)(−1850) ⇒ (1900) = 1650 = 1260(1900−1850) ⇒ ln 1650 1260 = (50) ⇒ = 50 1 ln 1650 1260 ≈ 0005393. So with this model, we estimate (1950) = 1260(1950−1850) ≈ 2161 million. This is still too low, but closer than the estimate of (1950) in part (a). (c) The exponential model gives () = (1900)(−1900) ⇒ (1950) = 2560 = 1650(1950−1900) ⇒ ln 2560 1650 = (50) ⇒ = 50 1 ln 2560 1650 ≈ 0008785. With this model, we estimate (2000) = 1650(2000−1900) ≈ 3972 million. This is much too low. The discrepancy is explained by the fact that the world birth rate (average yearly number of births per person) is about the same as always, whereas the mortality rate (especially the infant mortality rate) is much lower, owing mostly to advances in medical science and to the wars in the first part of the twentieth century. The exponential model assumes, among other things, that the birth and mortality rates will remain constant. 6. (a) Let () be the population (in millions) in the year . Since the initial time is the year 1950, we substitute − 1950 for in Theorem 2, and find that the exponential model gives () = (1950)(−1950) ⇒ (1960) = 100 = 83(1960−1950) ⇒ 100 83 = 10 ⇒ = 10 1 ln 100 83 ≈ 00186. With this model, we estimate (1980) = 83(1980−1950) = 8330 ≈ 145 million, which is an underestimate of the actual population of 150 million. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.8 EXPONENTIAL GROWTH AND DECAY ¤ 243 (b) As in part (a), () = (1960)(−1960) ⇒ (1980) = 150 = 10020 ⇒ 20 = ln 150 100 ⇒ = 1 20 ln 3 2 ≈ 00203. Thus, (2000) = 10040 = 225 million, which is an overestimate of the actual population of 214 million. (c) As in part (a), () = (1980)(−1980) ⇒ (2000) = 214 = 15020 ⇒ 20 = ln 214 150 ⇒ = 1 20 ln 214 150 ≈ 00178. Thus, (2010) = 15030 ≈ 256, which is an overestimate of the actual population of 243 million. (d) (2020) = 150(2020−1980) ≈ 305 million. This estimate will probably be an overestimate since this model gave us an overestimate in part (c) — indicating that is too large. Creating a model with more recent data would likely result in an improved estimate. 7. (a) If = [N2O5] then by Theorem 2, = −00005 ⇒ () = (0)−00005 = −00005. (b) () = −00005 = 09 ⇒ −00005 = 09 ⇒ −00005 = ln 09 ⇒ = −2000 ln 09 ≈ 211 s 8. (a) The mass remaining after days is () = (0) = 50. Since the half-life is 28 days, (28) = 5028 = 25 ⇒ 28 = 1 2 ⇒ 28 = ln 1 2 ⇒ = −(ln 2)28, so () = 50−(ln 2)28 = 50 · 2−28. (b) (40) = 50 · 2−4028 ≈ 186 mg (d) (c) () = 2 ⇒ 2 = 50 · 2−28 ⇒ 50 2 = 2−28 ⇒ (−28) ln 2 = ln 25 1 ⇒ = −28 ln 25 1 ln 2 ≈ 130 days 9. (a) If () is the mass (in mg) remaining after years, then () = (0) = 100. (30) = 10030 = 1 2(100) ⇒ 30 = 1 2 ⇒ = −(ln 2)30 ⇒ () = 100−(ln 2)30 = 100 · 2−30 (b) (100) = 100 · 2−10030 ≈ 992 mg (c) 100−(ln 2)30 = 1 ⇒ −(ln 2)30 = ln 100 1 ⇒ = −30 ln 0 ln 2 01 ≈ 1993 years 10. (a) If () is the mass after days and (0) = , then () = . (1) = = 0945 ⇒ = 0945 ⇒ = ln 0945. Then (ln 0945) = 1 2 ⇔ ln (ln 0945) = ln 1 2 ⇔ (ln 0945) = ln 1 2 ⇔ = − ln 0 ln 2 945 ≈ 1225 years. (b) (ln 0945) = 020 ⇔ (ln 0945) = ln 1 5 ⇔ = − ln 0 ln 5 945 ≈ 2845 years 11. Let () be the level of radioactivity. Thus, () = (0)− and is determined by using the half-life: (5730) = 1 2 (0) ⇒ (0)−(5730) = 1 2(0) ⇒ −5730 = 1 2 ⇒ −5730 = ln 1 2 ⇒ = − ln 1 2 5730 = ln 2 5730. If 74% of the 14C remains, then we know that () = 074(0) ⇒ 074 = −(ln 2)5730 ⇒ ln 074 = − ln 2 5730 ⇒ = − 5730(ln 074) ln 2 ≈ 2489 ≈ 2500 years. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.244 ¤ CHAPTER 3 DIFFERENTIATION RULES 12. From Exercise 11, we have the model () = (0)− with = (ln 2)5730. Thus, (68,000,000) = (0)−68000000 ≈ (0) · 0 = 0. There would be an undetectable amount of 14C remaining for a 68-million-year-old dinosaur. Now let () = 01% (0), so 0001(0) = (0)− ⇒ 0001 = − ⇒ ln 0001 = − ⇒ = ln 0001 − = ln 0001 −(ln 2)5730 ≈ 57,104, which is the maximum age of a fossil that we could date using 14C. 13. Let measure time since a dinosaur died in millions of years, and let () be the amount of 40K in the dinosaur’s bones at time . Then () = (0)− and is determined by the half-life: (1250) = 1 2(0) ⇒ (0)−(1250) = 1 2(0) ⇒ −1250 = 1 2 ⇒ −1250 = ln 1 2 ⇒ = − ln 1 2 1250 = ln 2 1250 . To determine if a dinosaur dating of 68 million years is possible, we find that (68) = (0)−(68) ≈ 0963(0), indicating that about 96% of the 40K is remaining, which is clearly detectable. To determine the maximum age of a fossil by using 40K, we solve () = 01%(0) for . (0)− = 0001(0) ⇔ − = 0001 ⇔ − = ln 0001 ⇔ = ln 0001 −(ln 2)1250 ≈ 12,457 million, or 12457 billion years. 14. From the information given, we know that = 2 ⇒ = 2 by Theorem 2. To calculate we use the point (0 5): 5 = 2(0) ⇒ = 5. Thus, the equation of the curve is = 52. 15. (a) Using Newton’s Law of Cooling, = ( − ), we have = ( − 75). Now let = − 75, so (0) = (0) − 75 = 185 − 75 = 110, so is a solution of the initial-value problem = with (0) = 110 and by Theorem 2 we have () = (0) = 110. (30) = 11030 = 150 − 75 ⇒ 30 = 110 75 = 15 22 ⇒ = 30 1 ln 15 22, so () = 110 30 1 ln( 15 22) and (45) = 110 45 30 ln( 15 22) ≈ 62◦F. Thus, (45) ≈ 62 + 75 = 137◦F. (b) () = 100 ⇒ () = 25. () = 110 30 1 ln( 15 22) = 25 ⇒ 30 1 ln( 15 22) = 110 25 ⇒ 30 1 ln 15 22 = ln 110 25 ⇒ = 30 ln 25 110 ln 15 22 ≈ 116 min. 16. Let () be the temperature of the body hours after 1:30 PM. Then (0) = 325 and (1) = 303. Using Newton’s Law of Cooling, = ( − ), we have = ( − 20). Now let = − 20, so (0) = (0) − 20 = 325 − 20 = 125, so is a solution to the initial value problem = with (0) = 125 and by Theorem 2 we have () = (0) = 125. (1) = 303 − 20 ⇒ 103 = 125(1) ⇒ = 10 12.53 ⇒ = ln 10 12.53. The murder occurred when °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.8 EXPONENTIAL GROWTH AND DECAY ¤ 245 () = 37 − 20 ⇒ 12.5 = 17 ⇒ = 12 17.5 ⇒ = ln 12 17.5 ⇒ = ln 12 17.5 ln 10 12.53 ≈ −1588 h ≈ −95 minutes. Thus, the murder took place about 95 minutes before 1:30 PM, or 11:55 AM. 17. = ( − 20). Letting = − 20, we get = , so () = (0). (0) = (0) − 20 = 5 − 20 = −15, so (25) = (0)25 = −1525, and (25) = (25) − 20 = 10 − 20 = −10, so −1525 = −10 ⇒ 25 = 2 3. Thus, 25 = ln 2 3 and = 25 1 ln 2 3, so () = (0) = −15(125) ln(23). More simply, 25 = 2 3 ⇒ = 2 3125 ⇒ = 2 325 ⇒ () = −15 · 2 325. (a) (50) = 20 + (50) = 20 − 15 · 2 35025 = 20 − 15 · 2 32 = 20 − 20 3 = 13¯ 3 ◦C (b) 15 = () = 20 + () = 20 − 15 · 2 325 ⇒ 15 · 2 325 = 5 ⇒ 2 325 = 1 3 ⇒ (25) ln 2 3 = ln 1 3 ⇒ = 25 ln 1 3ln 2 3 ≈ 6774 min. 18. = ( − 20). Let = − 20. Then = , so () = (0) (0) = (0) − 20 = 95 − 20 = 75, so () = 75. When () = 70, = −1◦Cmin. Equivalently, = −1 when () = 50. Thus, −1 = = () = 50 and 50 = () = 75. The first relation implies = −150, so the second relation says 50 = 75−50. Thus, −50 = 2 3 ⇒ −50 = ln 2 3 ⇒ = −50 ln 2 3 ≈ 2027 min. 19. (a) Let () be the pressure at altitude . Then = ⇒ () = (0) = 1013. (1000) = 10131000 = 8714 ⇒ 1000 = ln 87 101 14 3 ⇒ = 1000 1 ln 87 101 14 3 ⇒ () = 1013 1000 1 ln( 87 10114 3), so (3000) = 10133 ln( 87 101 14 3) ≈ 645 kPa. (b) (6187) = 1013 6187 1000 ln( 87 101 14 3) ≈ 399 kPa 20. (a) Using = 01 + with 0 = 1000, = 008, and = 3, we have: (i) Annually: = 1; = 10001 + 01081·3 = $125971 (ii) Quarterly: = 4; = 10001 + 04084·3 = $126824 (iii) Monthly: = 12; = 10001 + 012 0812·3 = $127024 (iv) Weekly: = 52 = 10001 + 052 0852·3 = $127101 (v) Daily: = 365; = 10001 + 0365 08365·3 = $127122 (vi) Hourly: = 365 · 24; = 10001 + 365 008 · 24365·24·3 = $127125 (vii) Continuously: = 1000(008)3 = $127125 (b) 010(3) = $134986, 008(3) = $127125, and 006(3) = $119722. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.246 ¤ CHAPTER 3 DIFFERENTIATION RULES 21. (a) Using = 01 + with 0 = 3000, = 005, and = 5, we have: (i) Annually: = 1; = 30001 + 01051·5 = $382884 (ii) Semiannually: = 2; = 30001 + 02052·5 = $384025 (iii) Monthly: = 12; = 30001 + 012 0512·5 = $385008 (iv) Weekly: = 52; = 30001 + 052 0552·5 = $385161 (v) Daily: = 365; = 30001 + 0365 05365·5 = $385201 (vi) Continuously: = 3000(005)5 = $385208 (b) = 005 and (0) = 3000. 22. (a) 0006 = 20 ⇔ 006 = 2 ⇔ 006 = ln 2 ⇔ = 50 3 ln 2 ≈ 1155, so the investment will double in about 1155 years. (b) The annual interest rate in = 0(1 + ) is . From part (a), we have = 0006. These amounts must be equal, so (1 + ) = 006 ⇒ 1 + = 006 ⇒ = 006 − 1 ≈ 00618 = 618%, which is the equivalent annual interest rate. APPLIED PROJECT Controlling Red Blood Cell Loss During Surgery 1. Let () be the volume of RBCs (in liters) at time (in hours). Since the total volume of blood is 5 L, the concentration of RBCs is 5. The patient bleeds 2 L of blood in 4 hours, so = − 2 4 · 5 = − 1 10 From Section 3.8, we know that = has solution () = (0). In this case, (0) = 45% of 5 = 9 4 and = − 1 10, so () = 9 4−10. At the end of the operation, the volume of RBCs is (4) = 9 4−04 ≈ 151 L. 2. Let be the volume of blood that is extracted and replaced with saline solution. Let () be the volume of RBCs with the ANH procedure. Then (0) is 45% of (5 − ), or 20 9 (5 − ), and hence () = 20 9 (5 − )−10. We want (4) ≥ 25% of 5 ⇔ 20 9 (5 − )−04 ≥ 5 4 ⇔ 5 − ≥ 25 9 04 ⇔ ≤ 5 − 25 9 04 ≈ 086 L. To maximize the effect of the ANH procedure, the surgeon should remove 086 L of blood and replace it with saline solution. 3. The RBC loss without the ANH procedure is (0) − (4) = 9 4 − 9 4−04 ≈ 074 L. The RBC loss with the ANH procedure is (0) − (4) = 20 9 (5 − ) − 20 9 (5 − )−04 = 20 9 (5 − )(1 − −04). Now let = 5 − 25 9 04 [from Problem 2] to get (0) − (4) = 20 9 5 − 5 − 25 9 04(1 − 04) = 20 9 · 25 9 04(1 − 04) = 5 4(04 − 1) ≈ 061 L. Thus, the ANH procedure reduces the RBC loss by about 074 − 061 = 013 L (about 44 fluid ounces). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.9 RELATED RATES ¤ 247 3.9 Related Rates 1. = 3 ⇒ = = 32 2. (a) = 2 ⇒ = = 2 (b) = 2 = 2(30 m)(1 ms) = 60 m2s 3. Let denote the side of a square. The square’s area is given by = 2. Differentiating with respect to gives us = 2 . When = 16, = 4. Substitution 4 for and 6 for gives us = 2(4)(6) = 48 cm2s. 4. = ⇒ = · + · = 20(3) + 10(8) = 140 cm2s. 5. = 2 = (5)2 = 25 ⇒ = 25 ⇒ 3 = 25 ⇒ = 253 mmin. 6. = 4 33 ⇒ = 4 3 · 32 ⇒ = 4 1 2 · 802(4) = 25,600 mm3s. 7. = 42 ⇒ = 4 · 2 ⇒ = 4 · 2 · 8 · 2 = 128 cm2min. 8. (a) = 1 2 sin ⇒ = 1 2 cos = 1 2(2)(3)cos 3 (02) = 3 1 2(02) = 03 cm2min. (b) = 1 2 sin ⇒ = 1 2 cos + sin = 1 2(2)3cos 3 (02) + sin 3 (15) = 3 1 2(02) + 1 2√3 3 2 = 03 + 3 4√3 cm2/min [≈ 16] (c) = 1 2 sin ⇒ = 1 2 sin + sin + cos [by Exercise 3.2.61(a)] = 12 (25)(3) 1 2√3 + (2)(15) 1 2√3 + (2)(3) 1 2(02) = 15 8 √3 + 3 4√3 + 03 = 21 8 √3 + 03 cm2min [≈ 485] Note how this answer relates to the answer in part (a) [ changing] and part (b) [ and changing]. 9. (a) = √2 + 1 and = 3 ⇒ = = 1 2(2 + 1)−12 · 2 · 3 = √23+ 1. When = 4, = √39 = 1. (b) = √2 + 1 ⇒ 2 = 2 + 1 ⇒ 2 = 2 − 1 ⇒ = 1 22 − 1 2 and = 5 ⇒ = = · 5 = 5. When = 12, = √25 = 5, so = 5(5) = 25. 10. (a) (42 + 92) = (36) ⇒ 8 + 18 = 0 ⇒ 4 + 9 = 0 ⇒ 4(2) + 932√513 = 0 ⇒ 8 = −2√5 ⇒ = −14√5 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.248 ¤ CHAPTER 3 DIFFERENTIATION RULES (b) 4 + 9 = 0 ⇒ 4(−2)(3) + 932√5 = 0 ⇒ 6√5 = 24 ⇒ = √45 11. (2 + 2 + 2) = (9) ⇒ 2 + 2 + 2 = 0 ⇒ + + = 0. If = 5, = 4 and ( ) = (2 2 1), then 2(5) + 2(4) + 1 = 0 ⇒ = −18. 12. () = (8) ⇒ + = 0. If = −3 cms and ( ) = (4 2), then 4(−3) + 2 = 0 ⇒ = 6. Thus, the -coordinate is increasing at a rate of 6 cms. 13. (a) Given: a plane flying horizontally at an altitude of 1 mi and a speed of 500 mih passes directly over a radar station. If we let be time (in hours) and be the horizontal distance traveled by the plane (in mi), then we are given that = 500 mih. (b) Unknown: the rate at which the distance from the plane to the station is increasing when it is 2 mi from the station. If we let be the distance from the plane to the station, then we want to find when = 2 mi. (c) (d) By the Pythagorean Theorem, 2 = 2 + 1 ⇒ 2 () = 2 (). (e) = = (500). Since 2 = 2 + 1, when = 2, = √3, so = √3 2 (500) = 250 √3 ≈ 433 mih. 14. (a) Given: the rate of decrease of the surface area is 1 cm2min. If we let be time (in minutes) and be the surface area (in cm2), then we are given that = −1 cm2s. (c) (b) Unknown: the rate of decrease of the diameter when the diameter is 10 cm. If we let be the diameter, then we want to find when = 10 cm. (d) If the radius is and the diameter = 2, then = 1 2 and = 42 = 4 1 22 = 2 ⇒ = = 2 . (e) −1 = = 2 ⇒ = −2 1 . When = 10, = −201 . So the rate of decrease is 201 cmmin. 15. (a) Given: a man 6 ft tall walks away from a street light mounted on a 15-ft-tall pole at a rate of 5 fts. If we let be time (in s) and be the distance from the pole to the man (in ft), then we are given that = 5 fts. (b) Unknown: the rate at which the tip of his shadow is moving when he is 40 ft from the pole. If we let be the distance from the man to the tip of his shadow (in ft), then we want to find ( + ) when = 40 ft. (c) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.9 RELATED RATES ¤ 249 (d) By similar triangles, 15 6 = + ⇒ 15 = 6 + 6 ⇒ 9 = 6 ⇒ = 2 3. (e) The tip of the shadow moves at a rate of ( + ) = + 23 = 53 = 5 3(5) = 25 3 fts. 16. (a) Given: at noon, ship A is 150 km west of ship B; ship A is sailing east at 35 kmh, and ship B is sailing north at 25 kmh. If we let be time (in hours), be the distance traveled by ship A (in km), and be the distance traveled by ship B (in km), then we are given that = 35 kmh and = 25 kmh. (b) Unknown: the rate at which the distance between the ships is changing at 4:00 PM. If we let be the distance between the ships, then we want to find when = 4 h. (c) (d) 2 = (150 − )2 + 2 ⇒ 2 = 2(150 − )− + 2 (e) At 4:00 PM, = 4(35) = 140 and = 4(25) = 100 ⇒ = (150 − 140)2 + 1002 = √10,100. So = 1 ( − 150) + = −10(35) + 100(25) √10,100 = √215 101 ≈ 214 kmh. 17. We are given that = 60 mih and = 25 mih. 2 = 2 + 2 ⇒ 2 = 2 + 2 ⇒ = + ⇒ = 1 + . After 2 hours, = 2 (60) = 120 and = 2 (25) = 50 ⇒ = √1202 + 502 = 130, so = 1 + = 120(60) + 50(25) 130 = 65 mih. 18. We are given that = 16 ms. By similar triangles, 12 = 2 ⇒ = 24 ⇒ = − 24 2 = − 24 2 (16). When = 8, = −24(1 646) = −06 ms, so the shadow is decreasing at a rate of 06 ms. 19. We are given that = 4 fts and = 5 fts. 2 = ( + )2 + 5002 ⇒ 2 = 2( + ) + . 15 minutes after the woman starts, we have = (4 fts)(20 min)(60 smin) = 4800 ft and = 5 · 15 · 60 = 4500 ⇒ = (4800 + 4500)2 + 5002 = √86,740,000, so = + + = √4800 + 4500 86,740,000 (4 + 5) = √837 8674 ≈ 899 fts °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.250 ¤ CHAPTER 3 DIFFERENTIATION RULES 20. We are given that = 24 fts. (a) 2 = (90 − )2 + 902 ⇒ 2 = 2(90 − )− . When = 45, = √452 + 902 = 45 √5, so = 90 − − = 4545 √5 (−24) = −√245, so the distance from second base is decreasing at a rate of √245 ≈ 107 fts. (b) Due to the symmetric nature of the problem in part (a), we expect to get the same answer— and we do. 2 = 2 + 902 ⇒ 2 = 2 . When = 45, = 45 √5, so = 4545 √5(24) = √245 ≈ 107 fts. 21. = 1 2, where is the base and is the altitude. We are given that = 1 cmmin and = 2 cm2min. Using the Product Rule, we have = 1 2 + . When = 10 and = 100, we have 100 = 1 2(10) ⇒ 1 2 = 10 ⇒ = 20, so 2 = 1 220 · 1 + 10 ⇒ 4 = 20 + 10 ⇒ = 4 −1020 = −16 cmmin. 22. Given = −1 ms, find when = 8 m. 2 = 2 + 1 ⇒ 2 = 2 ⇒ = = − . When = 8, = √65, so = − √65 8 . Thus, the boat approaches the dock at √65 8 ≈ 101 ms. 23. We are given that = 35 kmh and = 25 kmh. 2 = ( + )2 + 1002 ⇒ 2 = 2( + ) + . At 4:00 PM, = 4(35) = 140 and = 4(25) = 100 ⇒ = (140 + 100)2 + 1002 = √67,600 = 260, so = + + = 140 + 100 260 (35 + 25) = 720 13 ≈ 554 kmh. 24. The distance of the particle to the origin is given by = 2 + 2, so 2 = 2 + [2 sin(2)]2 ⇒ 2 = 2 + 4 · 2 sin2 cos2 · 2 ⇒ = + 2 sin2 cos2 . When ( ) = 13 1, = 1 32 + 12 = 10 9 = 13 √10, so 13 √10 = 13√10 + 2 sin 6 cos 6 · √10 ⇒ 1 3 = 1 3 + 21212√3 ⇒ = 1 + 3√23 cms. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.9 RELATED RATES ¤ 251 25. If = the rate at which water is pumped in, then = − 10,000, where = 1 32 is the volume at time . By similar triangles, 2 = 6 ⇒ = 13 ⇒ = 1 3 1 32 = 27 3 ⇒ = 9 2 . When = 200 cm, = 20 cmmin, so − 10,000 = 9 (200)2(20) ⇒ = 10,000 + 8009,000 ≈ 289,253 cm3min. 26. By similar triangles, 3 1 = , so = 3. The trough has volume = 1 2(10) = 5(3) = 152 ⇒ 12 = = 30 ⇒ = 52. When = 1 2, = 2 5 · 1 2 = 4 5 ftmin. 27. The figure is labeled in meters. The area of a trapezoid is 12 (base1 + base2)(height), and the volume of the 10-meter-long trough is 10. Thus, the volume of the trapezoid with height is = (10) 1 2[03 + (03 + 2)]. By similar triangles, = 025 05 = 1 2 , so 2 = ⇒ = 5(06 + ) = 3 + 52. Now = ⇒ 02 = (3 + 10) ⇒ = 3 + 10 02 . When = 03, = 02 3 + 10(03) = 02 6 mmin = 1 30 mmin or 10 3 cmmin. 28. The figure is drawn without the top 3 feet. = 1 2( + 12)(20) = 10( + 12) and, from similar triangles, = 6 6 and = 16 6 = 8 3 , so = + 12 + = + 12 + 8 3 = 12 + 11 3 . Thus, = 1024 + 113 = 240 + 11032 and so 08 = = 240 + 220 3 . When = 5, = 08 240 + 5(2203) = 3 2275 ≈ 000132 ftmin. 29. We are given that = 30 ft3min. = 132 = 132 2 = 123 ⇒ = ⇒ 30 = 4 2 ⇒ = 1202 . When = 10 ft, = 120 102 = 6 5 ≈ 038 ftmin. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.252 ¤ CHAPTER 3 DIFFERENTIATION RULES 30. We are given = 8 fts. cot = 100 ⇒ = 100 cot ⇒ = −100 csc2 ⇒ = −sin 100 2 · 8. When = 200, sin = 100 200 = 12 ⇒ = − (12)2 100 · 8 = − 1 50 rads. The angle is decreasing at a rate of 50 1 rads. 31. The area of an equilateral triangle with side is given by = 1 4√3 2. = 14 √3 · 2 = 14 √3 · 2(30)(10) = 150√3 cm2min. 32. cos = 10 ⇒ − sin = 1 10 . From Example 2, = 1 and when = 6, = 8, so sin = 8 10 . Thus, − 8 10 = 1 10 (1) ⇒ = − 1 8 rads. 33. From the figure and given information, we have 2 + 2 = 2, = −015 m s, and = 02 m s when = 3 m. Differentiating implicitly with respect to , we get 2 + 2 = 2 ⇒ 2 + 2 = 0 ⇒ = − . Substituting the given information gives us (−015) = −3(02) ⇒ = 4 m. Thus, 32 + 42 = 2 ⇒ 2 = 25 ⇒ = 5 m. 34. According to the model in Example 2, = − → −∞ as → 0, which doesn’t make physical sense. For example, the model predicts that for sufficiently small , the tip of the ladder moves at a speed greater than the speed of light. Therefore the model is not appropriate for small values of . What actually happens is that the tip of the ladder leaves the wall at some point in its descent. For a discussion of the true situation see the article “The Falling Ladder Paradox” by Paul Scholten and Andrew Simoson in The College Mathematics Journal, 27, (1), January 1996, pages 49–54. Also see “On Mathematical and Physical Ladders” by M. Freeman and P. Palffy-Muhoray in the American Journal of Physics, 53 (3), March 1985, pages 276–277. 35. The area of a sector of a circle with radius and angle is given by = 1 22. Here is constant and varies, so = 1 2 2 . The minute hand rotates through 360◦ = 2 radians each hour, so = 1 22(2) = 2 cm2h. This answer makes sense because the minute hand sweeps through the full area of a circle, 2, each hour. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.9 RELATED RATES ¤ 253 36. The volume of a hemisphere is 2 33, so the volume of a hemispherical basin of radius 30 cm is 2 3(30)3 = 18,000 cm3. If the basin is half full, then = 2 − 1 33 ⇒ 9000 = 302 − 1 33 ⇒ 1 33 − 302 + 9000 = 0 ⇒ = ≈ 1958 [from a graph or numerical rootfinder; the other two solutions are less than 0 and greater than 30]. = 302 − 1 33 ⇒ = 60 − 2 ⇒ 2 min L 1000 cmL 3 = (60 − 2) ⇒ = 2000 (60 − 2) ≈ 0804 cmmin. 37. Differentiating both sides of = with respect to and using the Product Rule gives us + = 0 ⇒ = − . When = 600, = 150 and = 20, so we have = −600 150 (20) = −80. Thus, the volume is decreasing at a rate of 80 cm3min. 38. 14 = ⇒ · 14 04 + 14 = 0 ⇒ = − ·1144 04 = −14 . When = 400, = 80 and = −10, so we have = −1400 4(80)(−10) = 250 7 . Thus, the volume is increasing at a rate of 250 7 ≈ 36 cm3min. 39. With 1 = 80 and 2 = 100, 1 = 1 1 + 1 2 = 1 80 + 1 100 = 180 8000 = 9 400, so = 400 9 . Differentiating 1 = 11 + 12 with respect to , we have − 1 2 = − 1 21 1 − 1 22 2 ⇒ = 2112 1 + 122 2 . When 1 = 80 and 2 = 100, = 4002 92 80 12 (03) + 100 1 2 (02) = 107 810 ≈ 0132 Ωs. 40. We want to find when = 18 using = 0007 23 and = 012253. = = 0007 · 2 3 −13(012 · 253 · 153)1020 ,000 −,15 000 = 0007 · 2 3(012 · 18 253)−13012 · 253 · 1815310 57 ≈ 1045 × 10−8 gyr 41. We are given = 2◦min = 90 radmin. By the Law of Cosines, 2 = 122 + 152 − 2(12)(15) cos = 369 − 360 cos ⇒ 2 = 360 sin ⇒ = 180 sin . When = 60◦, = √369 − 360 cos 60◦ = √189 = 3 √21, so = 180 sin 60◦ 3 √21 90 = √3 3 √21 = √7 21 ≈ 0396 mmin. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.254 ¤ CHAPTER 3 DIFFERENTIATION RULES 42. Using for the origin, we are given = −2 fts and need to find when = −5. Using the Pythagorean Theorem twice, we have √2 + 122 + 2 + 122 = 39, the total length of the rope. Differentiating with respect to , we get √2 + 122 + 2 + 122 = 0, so = − √22 + 12 + 1222 . Now when = −5, 39 = (−5)2 + 122 + 2 + 122 = 13 + 2 + 122 ⇔ 2 + 122 = 26, and = √262 − 122 = √532. So when = −5, = − (−5)(26) √532 (13)(−2) = −√10 133 ≈ −087 fts. So cart is moving towards at about 087 fts. 43. (a) By the Pythagorean Theorem, 40002 + 2 = 2. Differentiating with respect to , we obtain 2 = 2 . We know that = 600 fts, so when = 3000 ft, = √40002 + 30002 = √25,000,000 = 5000 ft and = = 3000 5000 (600) = 1800 5 = 360 fts. (b) Here tan = 4000 ⇒ (tan ) = 4000 ⇒ sec2 = 4000 1 ⇒ = cos 4000 2 . When = 3000 ft, = 600 fts, = 5000 and cos = 4000 = 4000 5000 = 45, so = (4 4000 5)2 (600) = 0096 rads. 44. We are given that = 4(2) = 8 radmin. = 3 tan ⇒ = 3 sec2 . When = 1, tan = 1 3, so sec2 = 1 + 1 32 = 10 9 and = 3 10 9 (8) = 80 3 ≈ 838 kmmin. 45. cot = 5 ⇒ − csc2 = 1 5 ⇒ − csc 3 2−6 = 15 ⇒ = 5 6 √232 = 10 9 kmmin [≈ 130 mih] 46. We are given that = 2 rad 2 min = radmin By the Pythagorean Theorem, when = 6, = 8, so sin = 10 6 and cos = 10 8 . From the figure, sin = 10 ⇒ = 10 sin , so = 10 cos = 1010 8 = 8 mmin. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.9 RELATED RATES ¤ 255 47. We are given that = 300 kmh. By the Law of Cosines, 2 = 2 + 12 − 2(1)() cos 120◦ = 2 + 1 − 2− 1 2 = 2 + + 1, so 2 = 2 + ⇒ = 22+ 1 . After 1 minute, = 300 60 = 5 km ⇒ = √52 + 5 + 1 = √31 km ⇒ = 2(5) + 1 2 √31 (300) = 1650 √31 ≈ 296 kmh. 48. We are given that = 3 mih and = 2 mih. By the Law of Cosines, 2 = 2 + 2 − 2 cos 45◦ = 2 + 2 − √2 ⇒ 2 = 2 + 2 − √2 − √2 . After 15 minutes = 1 4 h, we have = 3 4 and = 2 4 = 1 2 ⇒ 2 = 3 42 + 2 42 − √2 3 4 2 4 ⇒ = 13 − 6 √2 4 and = 2 13 − 6 √2 2 3 43 + 2 1 22 − √2 3 42 − √2 1 23 = 13 −2 6 √2 13 −26 √2 = 13 − 6 √2 ≈ 2125 mih. 49. Let the distance between the runner and the friend be . Then by the Law of Cosines, 2 = 2002 + 1002 − 2 · 200 · 100 · cos = 50,000 − 40,000 cos (). Differentiating implicitly with respect to , we obtain 2 = −40,000(− sin ) . Now if is the distance run when the angle is radians, then by the formula for the length of an arc on a circle, = , we have = 100, so = 1 100 ⇒ = 1 100 = 7 100 . To substitute into the expression for , we must know sin at the time when = 200, which we find from (): 2002 = 50,000 − 40,000 cos ⇔ cos = 1 4 ⇒ sin = 1 − 1 42 = √415. Substituting, we get 2(200) = 40,000 √415 100 7 ⇒ = 7 √415 ≈ 678 ms. Whether the distance between them is increasing or decreasing depends on the direction in which the runner is running. 50. The hour hand of a clock goes around once every 12 hours or, in radians per hour, 2 12 = 6 radh. The minute hand goes around once an hour, or at the rate of 2 radh. So the angle between them (measuring clockwise from the minute hand to the hour hand) is changing at the rate of = 6 − 2 = − 116 radh. Now, to relate to , we use the Law of Cosines: 2 = 42 + 82 − 2 · 4 · 8 · cos = 80 − 64 cos (). Differentiating implicitly with respect to , we get 2 = −64(− sin ) . At 1:00, the angle between the two hands is °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.256 ¤ CHAPTER 3 DIFFERENTIATION RULES one-twelfth of the circle, that is, 212 = 6 radians. We use () to find at 1:00: = 80 − 64 cos 6 = 80 − 32 √3. Substituting, we get 2 = 64 sin 6 −116 ⇒ = 264 80 1 2−−32 116√3 = −3 8088 −32 √3 ≈ −186. So at 1:00, the distance between the tips of the hands is decreasing at a rate of 186 mmh ≈ 0005 mms. 3.10 Linear Approximations and Differentials 1. () = 3 − 2 + 3 ⇒ 0() = 32 − 2, so (−2) = −9 and 0(−2) = 16. Thus, () = (−2) + 0(−2)( − (−2)) = −9 + 16( + 2) = 16 + 23. 2. () = sin ⇒ 0() = cos , so 6 = 1 2 and 0 6 = 1 2√3. Thus, () = 6 + 0 6 − 6 = 1 2 + 1 2√3 − 6 = 1 2√3 + 1 2 − 12 1 √3 . 3. () = √ ⇒ 0() = 1 2−12 = 1(2√), so (4) = 2 and 0(4) = 1 4. Thus, () = (4) + 0(4)( − 4) = 2 + 1 4( − 4) = 2 + 1 4 − 1 = 1 4 + 1. 4. () = 2 ⇒ 0() = 2 ln 2, so (0) = 1 and 0(0) = ln 2. Thus, () = (0) + 0(0)( − 0) = 1 + (ln 2). 5. () = √1 − ⇒ 0() = −1 2 √1 − , so (0) = 1 and 0(0) = − 1 2. Therefore, √1 − = () ≈ (0) + 0(0)( − 0) = 1 + − 1 2( − 0) = 1 − 1 2. So √09 = √1 − 01 ≈ 1 − 1 2(01) = 095 and √099 = √1 − 001 ≈ 1 − 1 2(001) = 0995. 6. () = √3 1 + = (1 + )13 ⇒ 0() = 1 3(1 + )−23, so (0) = 1 and 0(0) = 1 3. Therefore, √3 1 + = () ≈ (0) + 0(0)( − 0) = 1 + 1 3. So √3 095 = 3 1 + (−005) ≈ 1 + 1 3(−005) = 0983, and √3 11 = √3 1 + 01 ≈ 1 + 1 3(01) = 103. 7. () = ln(1 + ) ⇒ 0() = 1 1 + , so (0) = 0 and 0(0) = 1. Thus, () ≈ (0) + 0(0)( − 0) = 0 + 1() = . We need ln(1 + ) − 01 ln(1 + ) + 01, which is true when −0383 0516. 8. () = (1 + )−3 ⇒ 0() = −3(1 + )−4, so (0) = 1 and 0(0) = −3. Thus, () ≈ (0) + 0(0)( − 0) = 1 − 3. We need (1 + )−3 − 01 1 − 3 (1 + )−3 + 01, which is true when −0116 0144. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.10 LINEAR APPROXIMATIONS AND DIFFERENTIALS ¤ 257 9. () = √4 1 + 2 ⇒ 0() = 1 4(1 + 2)−34(2) = 1 2(1 + 2)−34, so (0) = 1 and 0(0) = 1 2. Thus, () ≈ (0) + 0(0)( − 0) = 1 + 1 2. We need √4 1 + 2 − 01 1 + 1 2 √4 1 + 2 + 01, which is true when −0368 0677. 10. () = cos ⇒ 0() = (− sin ) + (cos ) = (cos − sin ), so (0) = 1 and 0(0) = 1. Thus, () ≈ (0) + 0(0)( − 0) = 1 + . We need cos − 01 1 + cos + 01, which is true when −0762 0607. 11. (a) The differential is defined in terms of by the equation = 0() . For = () = −4, 0() = −4(−4) + −4 · 1 = −4(−4 + 1), so = (1 − 4)−4. (b) For = () = √1 − 4, 0() = 1 2(1 − 4)−12(−43) = −√12−3 4 , so = −√12−3 4 . 12. (a) For = () = 1 + 2 1 + 3 , 0() = (1 + 3)(2) (1 + 3 − (1 + 2 )2 )(3) = (1 + 3 −1)2 , so = (1 + 3 −1)2 . (b) For = () = 2 sin 2, 0() = 2(cos 2)(2) + (sin 2)(2), so = 2( cos 2 + sin 2) . 13. (a) For = () = tan √, 0() = sec2 √ · 1 2 −12 = sec2 √ 2√ , so = sec 2√2 √ . (b) For = () = 1 − 2 1 + 2 , 0() = (1 + 2)(−2) − (1 − 2)(2) (1 + 2)2 = −2[(1 + 2) + (1 − 2)] (1 + 2)2 = −2(2) (1 + 2)2 = −4 (1 + 2)2 , so = −4 (1 + 2)2 . 14. (a) For = () = ln(sin ), 0() = 1 sin cos = cot , so = cot . (b) For = () = 1 − , 0() = (1 − (1)− −)2(−) = [(1 −(1−)−)2(−)] = (1 −)2 , so = (1 − )2 . 15. (a) = 10 ⇒ = 10 · 10 1 = 10 1 10 (b) = 0 and = 01 ⇒ = 10 1 010(01) = 001. 16. (a) = cos ⇒ = −sin · = − sin (b) = 1 3 and = −002 ⇒ = − sin 3 (−002) = √32(002) = 001 √3 ≈ 0054. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.258 ¤ CHAPTER 3 DIFFERENTIATION RULES 17. (a) = √3 + 2 ⇒ = 1 2 (3 + 2)−12(2) = √3 + 2 (b) = 1 and = −01 ⇒ = √3 + 1 1 2 (−01) = 1 2(−01) = −005. 18. (a) = + 1 − 1 ⇒ = ( − 1)(1) − ( + 1)(1) ( − 1)2 = ( −−21)2 (b) = 2 and = 005 ⇒ = −2 (2 − 1)2 (005) = −2(005) = −01. 19. = () = 2 − 4, = 3, ∆ = 05 ⇒ ∆ = (35) − (3) = −175 − (−3) = 125 = 0() = (2 − 4) = (6 − 4)(05) = 1 20. = () = − 3, = 0, ∆ = −03 ⇒ ∆ = (−03) − (0) = −0273 − 0 = −0273 = 0() = (1 − 32) = (1 − 0)(−03) = −03 21. = () = √ − 2, = 3, ∆ = 08 ⇒ ∆ = (38) − (3) = √18 − 1 ≈ 034 = 0() = 1 2√ − 2 = 2(1) 1 (08) = 04 22. = () = , = 0, ∆ = 05 ⇒ ∆ = (05) − (0) = √ − 1 [≈ 065] = = 0(05) = 05 23. To estimate (1999)4, we’ll find the linearization of () = 4 at = 2. Since 0() = 43, (2) = 16, and 0(2) = 32, we have () = 16 + 32( − 2). Thus, 4 ≈ 16 + 32( − 2) when is near 2, so (1999)4 ≈ 16 + 32(1999 − 2) = 16 − 0032 = 15968. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.10 LINEAR APPROXIMATIONS AND DIFFERENTIALS ¤ 259 24. = () = 1 ⇒ = −12 . When = 4 and = 0002, = − 16 1 (0002) = − 8000 1 , so 1 4002 ≈ (4) + = 1 4 − 8000 1 = 1999 8000 = 0249875. 25. = () = √3 ⇒ = 1 3−23 . When = 1000 and = 1, = 1 3(1000)−23(1) = 300 1 , so √3 1001 = (1001) ≈ (1000) + = 10 + 300 1 = 10003 ≈ 10003. 26. = () = √ ⇒ = 1 2−12 . When = 100 and = 05, = 1 2(100)−12 1 2 = 40 1 , so √1005 = (1005) ≈ (100) + = 10 + 40 1 = 10025. 27. = () = ⇒ = . When = 0 and = 01, = 0(01) = 01, so 01 = (01) ≈ (0) + = 1 + 01 = 11. 28. = () = cos ⇒ = −sin . When = 30◦ [6] and = −1◦ [−180], = − sin 6 − 180 = − 1 2− 180 = 360 , so cos 29◦ = (29◦) ≈ (30◦) + = 1 2√3 + 360 ≈ 0875. 29. = () = sec ⇒ 0() = sec tan , so (0) = 1 and 0(0) = 1 · 0 = 0. The linear approximation of at 0 is (0) + 0(0)( − 0) = 1 + 0() = 1. Since 008 is close to 0, approximating sec 008 with 1 is reasonable. 30. = () = √ ⇒ 0() = 1(2√ ), so (4) = 2 and 0(4) = 1 4. The linear approximation of at 4 is (4) + 0(4)( − 4) = 2 + 1 4( − 4). Now (402) = √402 ≈ 2 + 1 4(002) = 2 + 0005 = 2005, so the approximation is reasonable. 31. = () = 1 ⇒ 0() = −12, so (10) = 01 and 0(10) = −001. The linear approximation of at 10 is (10) + 0(10)( − 10) = 01 − 001( − 10). Now (998) = 1998 ≈ 01 − 001(−002) = 01 + 00002 = 01002, so the approximation is reasonable. 32. (a) () = ( − 1)2 ⇒ 0() = 2( − 1), so (0) = 1 and 0(0) = −2. Thus, () ≈ () = (0) + 0(0)( − 0) = 1 − 2. () = −2 ⇒ 0() = −2−2, so (0) = 1 and 0(0) = −2. Thus, () ≈ () = (0) + 0(0)( − 0) = 1 − 2. () = 1 + ln(1 − 2) ⇒ 0() = −2 1 − 2 , so (0) = 1 and 0(0) = −2. Thus, () ≈ () = (0) + 0(0)( − 0) = 1 − 2. Notice that = = . This happens because , , and have the same function values and the same derivative values at = 0. (b) The linear approximation appears to be the best for the function since it is closer to for a larger domain than it is to and . The approximation looks worst for since moves away from faster than and do. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.260 ¤ CHAPTER 3 DIFFERENTIATION RULES 33. (a) If is the edge length, then = 3 ⇒ = 32 . When = 30 and = 01, = 3(30)2(01) = 270, so the maximum possible error in computing the volume of the cube is about 270 cm3. The relative error is calculated by dividing the change in , ∆ , by . We approximate ∆ with . Relative error = ∆ ≈ = 32 3 = 3 = 3030 1 = 001. Percentage error = relative error × 100% = 001 × 100% = 1%. (b) = 62 ⇒ = 12 . When = 30 and = 01, = 12(30)(01) = 36, so the maximum possible error in computing the surface area of the cube is about 36 cm2. Relative error = ∆ ≈ = 12 62 = 2 = 2030 1 = 0006. Percentage error = relative error × 100% = 0006 × 100% = 06%. 34. (a) = 2 ⇒ = 2 . When = 24 and = 02, = 2(24)(02) = 96, so the maximum possible error in the calculated area of the disk is about 96 ≈ 30 cm2. (b) Relative error = ∆ ≈ = 2 2 = 2 = 2(02) 24 = 02 12 = 1 60 = 0016. Percentage error = relative error ×100% = 0016 × 100% = 16%. 35. (a) For a sphere of radius , the circumference is = 2 and the surface area is = 42, so = 2 ⇒ = 42 2 = 2 ⇒ = 2 . When = 84 and = 05, = 2 (84)(05) = 84 , so the maximum error is about 84 ≈ 27 cm2. Relative error ≈ = 84 842 = 1 84 ≈ 0012 = 12% (b) = 4 3 3 = 4 3 2 3 = 632 ⇒ = 212 2 . When = 84 and = 05, = 1 22 (84)2(05) = 1764 2 , so the maximum error is about 1764 2 ≈ 179 cm3. The relative error is approximately = 17642 (84)3(62) = 1 56 ≈ 0018 = 18%. 36. For a hemispherical dome, = 2 33 ⇒ = 22 . When = 1 2(50) = 25 m and = 005 cm = 00005 m, = 2(25)2(00005) = 58 , so the amount of paint needed is about 58 ≈ 2 m3. 37. (a) = 2 ⇒ ∆ ≈ = 2 = 2 ∆ (b) The error is ∆ − = [( + ∆)2 − 2] − 2 ∆ = 2 + 2 ∆ + (∆)2 − 2 − 2 ∆ = (∆)2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.10 LINEAR APPROXIMATIONS AND DIFFERENTIALS ¤ 261 38. (a) sin = 20 ⇒ = 20 csc ⇒ = 20(− csc cot ) = −20 csc 30◦ cot 30◦ (±1◦) = −20(2)√3 ±180 = ±2 √9 3 So the maximum error is about ± 2 9 √3 ≈ ±121 cm. (b) The relative error is ∆ ≈ = ± 2 9 √3 20(2) = ± √3 180 ≈ ±003, so the percentage error is approximately ±3%. 39. = ⇒ = ⇒ = −2 . The relative error in calculating is ∆ ≈ = −( 2) = − . Hence, the relative error in calculating is approximately the same (in magnitude) as the relative error in . 40. = 4 ⇒ = 43 ⇒ = 43 4 = 4 . Thus, the relative change in is about 4 times the relative change in . So a 5% increase in the radius corresponds to a 20% increase in blood flow. 41. (a) = = 0 = 0 (b) () = () = = (c) ( + ) = ( + ) = + = + = + (d) () = () = + = + = + (e) = = − 2 = − 2 = − 2 (f ) () = () = −1 42. (a) () = sin ⇒ 0() = cos , so (0) = 0 and 0(0) = 1. Thus, () ≈ (0) + 0(0)( − 0) = 0 + 1( − 0) = . (b) [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.262 ¤ CHAPTER 3 DIFFERENTIATION RULES We want to know the values of for which = approximates = sin with less than a 2% difference; that is, the values of for which − sin sin 002 ⇔ −002 − sin sin 002 ⇔ −−0002 sin 02 sin −− sin sin 0 0 02 sin 02 sin if if sin sin 0 0 ⇔ 0 1 98 sin 02 sin 1 0 02 sin 98 sin if if sin sin 0 0 In the first figure, we see that the graphs are very close to each other near = 0. Changing the viewing rectangle and using an intersect feature (see the second figure) we find that = intersects = 102 sin at ≈ 0344. By symmetry, they also intersect at ≈ −0344 (see the third figure). Converting 0344 radians to degrees, we get 0344 180 ◦ ≈ 197◦ ≈ 20◦, which verifies the statement. 43. (a) The graph shows that 0(1) = 2, so () = (1) + 0(1)( − 1) = 5 + 2( − 1) = 2 + 3. (09) ≈ (09) = 48 and (11) ≈ (11) = 52. (b) From the graph, we see that 0() is positive and decreasing. This means that the slopes of the tangent lines are positive, but the tangents are becoming less steep. So the tangent lines lie above the curve. Thus, the estimates in part (a) are too large. 44. (a) 0() = √2 + 5 ⇒ 0(2) = √9 = 3. (195) ≈ (2) + 0(2)(195 − 2) = −4 + 3(−005) = −415. (205) ≈ (2) + 0(2)(205 − 2) = −4 + 3(005) = −385. (b) The formula 0() = √2 + 5 shows that 0() is positive and increasing. This means that the slopes of the tangent lines are positive and the tangents are getting steeper. So the tangent lines lie below the graph of . Hence, the estimates in part (a) are too small. LABORATORY PROJECT Taylor Polynomials 1. We first write the functions described in conditions (i), (ii), and (iii): () = + + 2 () = cos 0() = + 2 0() = − sin 00() = 2 00() = − cos So, taking = 0, our three conditions become (0) = (0): = cos 0 = 1 0(0) = 0(0): = − sin 0 = 0 00(0) = 00(0): 2 = − cos 0 = −1 ⇒ = − 1 2 The desired quadratic function is () = 1 − 1 22, so the quadratic approximation is cos ≈ 1 − 1 22. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.LABORATORY PROJECT TAYLOR POLYNOMIALS ¤ 263 The figure shows a graph of the cosine function together with its linear approximation () = 1 and quadratic approximation () = 1 − 1 22 near 0. You can see that the quadratic approximation is much better than the linear one. 2. Accuracy to within 01 means that cos − 1 − 1 22 01 ⇔ −01 cos − 1 − 1 22 01 ⇔ 01 1 − 1 22 − cos −0.1 ⇔ cos + 01 1 − 1 22 cos − 01 ⇔ cos − 01 1 − 1 22 cos + 01. From the figure we see that this is true between and . Zooming in or using an intersect feature, we find that the -coordinates of and are about ±126. Thus, the approximation cos ≈ 1 − 1 22 is accurate to within 01 when −126 126. 3. If () = + ( − ) + ( − )2, then 0() = + 2( − ) and 00() = 2. Applying the conditions (i), (ii), and (iii), we get () = (): = () 0() = 0(): = 0() 00() = 00(): 2 = 00() ⇒ = 1 2 00() Thus, () = + ( − ) + ( − )2 can be written in the form () = () + 0()( − ) + 1 2 00()( − )2. 4. From Example 3.10.1, we have (1) = 2, 0(1) = 1 4, and 0() = 1 2( + 3)−12. So 00() = − 1 4( + 3)−32 ⇒ 00(1) = − 32 1 . From Problem 3, the quadratic approximation () is √ + 3 ≈ (1) + 0(1)( −1) + 1 2 00(1)(−1)2 = 2 + 1 4( −1) − 64 1 ( −1)2. The figure shows the function () = √ + 3 together with its linear approximation () = 1 4 + 7 4 and its quadratic approximation (). You can see that () is a better approximation than () and this is borne out by the numerical values in the following chart. from () actual value from () √398 19950 199499373 199499375 √405 20125 201246118 201246094 √42 20500 204939015 204937500 5. () = 0 + 1( − ) + 2( − )2 + 3( − )3 + · · · + ( − ). If we put = in this equation, then all terms after the first are 0 and we get () = 0. Now we differentiate () and obtain 0 () = 1 + 22( − ) + 33( − )2 + 44( − )3 + · · · + ( − )−1. Substituting = gives 0 () = 1. Differentiating again, we have 00() = 22 + 2 · 33( − ) + 3 · 44( − 2) + · · · + ( − 1)( − )−2 and so °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.264 ¤ CHAPTER 3 DIFFERENTIATION RULES 00 () = 22. Continuing in this manner, we get 000() = 2 · 33 + 2 · 3 · 44( − ) + · · · + ( − 2)( − 1)( − )−3 and 000 () = 2 · 33. By now we see the pattern. If we continue to differentiate and substitute = , we obtain (4)() = 2 · 3 · 44 and in general, for any integer between 1 and , ()() = 2 · 3 · 4 · 5 · · · · · = ! ⇒ = ()() ! . Because we want and to have the same derivatives at , we require that = ()!() for = 1 2 . 6. () = () + 0()( − ) + 00() 2! ( − )2 + · · · + ()!()( − ). To compute the coefficients in this equation we need to calculate the derivatives of at 0: () = cos (0) = cos 0 = 1 0() = − sin 0(0) = − sin 0 = 0 00() = − cos 00(0) = −1 000() = sin 000(0) = 0 (4)() = cos (4)(0) = 1 We see that the derivatives repeat in a cycle of length 4, so (5)(0) = 0, (6)(0) = −1, (7)(0) = 0, and (8)(0) = 1. From the original expression for (), with = 8 and = 0, we have 8() = (0) + 0(0)( − 0) + 00(0) 2! ( − 0)2 + 000 3! (0)( − 0)3 + · · · + (8) 8!(0)( − 0)8 = 1 + 0 · + −1 2! 2 + 0 · 3 + 4! 1 4 + 0 · 5 + −6!16 + 0 · 7 + 8! 1 8 = 1 − 2! 2 + 4! 4 − 6! 6 + 8! 8 and the desired approximation is cos ≈ 1 − 2 2! + 4 4! − 6 6! + 8 8! . The Taylor polynomials 2, 4, and 6 consist of the initial terms of 8 up through degree 2, 4, and 6, respectively. Therefore, 2() = 1 − 2 2! , 4() = 1 − 2! 2 + 4! 4 , and 6() = 1 − 2 2! + 4 4! − 6 6! . We graph 2, 4, 6, 8, and : Notice that 2() is a good approximation to cos near 0, 4() is a good approximation on a larger interval, 6() is a better approximation, and 8() is better still. Each successive Taylor polynomial is a good approximation on a larger interval than the previous one. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.11 HYPERBOLIC FUNCTIONS ¤ 265 3.11 Hyperbolic Functions 1. (a) sinh 0 = 1 2(0 − −0) = 0 (b) cosh 0 = 1 2(0 + −0) = 1 2(1 + 1) = 1 2. (a) tanh 0 = (0 − −0)2 (0 + −0)2 = 0 (b) tanh 1 = 1 1 − + − −1 1 = 2 2 − + 1 1 ≈ 076159 3. (a) cosh(ln 5) = 1 2(ln 5 + −ln 5) = 1 25 + (ln 5)−1 = 1 2(5 + 5−1) = 1 25 + 1 5 = 13 5 (b) cosh 5 = 1 2(5 + −5) ≈ 7420995 4. (a) sinh 4 = 1 2(4 − −4) ≈ 2728992 (b) sinh(ln 4) = 1 2(ln 4 − −ln 4) = 1 24 − (ln 4)−1 = 1 2(4 − 4−1) = 1 24 − 1 4 = 15 8 5. (a) sech 0 = 1 cosh 0 = 1 1 = 1 (b) cosh−1 1 = 0 because cosh 0 = 1. 6. (a) sinh 1 = 1 2(1 − −1) ≈ 117520 (b) Using Equation 3, we have sinh−1 1 = ln1 + √12 + 1 = ln1 + √2 ≈ 088137. 7. sinh(−) = 1 2[− − −(−)] = 1 2(− − ) = − 1 2(− − ) = − sinh 8. cosh(−) = 1 2[− + −(−)] = 1 2(− + ) = 1 2( + −) = cosh 9. cosh + sinh = 1 2( + −) + 1 2( − −) = 1 2(2) = 10. cosh − sinh = 1 2( + −) − 1 2( − −) = 1 2(2−) = − 11. sinh cosh + cosh sinh = 1 2( − −) 1 2( + −) + 1 2( + −) 1 2( − −) = 14 [(+ + − − −+ − −−) + (+ − − + −+ − −−)] = 14 (2+ − 2−−) = 1 2[+ − −(+)] = sinh( + ) 12. cosh cosh + sinh sinh = 1 2( + −) 1 2( + −) + 1 2( − −) 1 2( − −) = 14 (+ + − + −+ + −−) + (+ − − − −+ + −−) = 14 (2+ + 2−−) = 1 2+ + −(+) = cosh( + ) 13. Divide both sides of the identity cosh2 − sinh2 = 1 by sinh2 : cosh2 sinh2 − sinh2 sinh2 = 1 sinh2 ⇔ coth2 − 1 = csch2 . 14. tanh( + ) = sinh( + ) cosh( + ) = sinh cosh + cosh sinh cosh cosh + sinh sinh = sinh cosh cosh cosh + cosh sinh cosh cosh cosh cosh cosh cosh + sinh sinh cosh cosh = tanh + tanh 1 + tanh tanh 15. Putting = in the result from Exercise 11, we have sinh 2 = sinh( + ) = sinh cosh + cosh sinh = 2 sinh cosh . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.266 ¤ CHAPTER 3 DIFFERENTIATION RULES 16. Putting = in the result from Exercise 12, we have cosh 2 = cosh( + ) = cosh cosh + sinh sinh = cosh2 + sinh2 . 17. tanh(ln ) = sinh(ln ) cosh(ln ) = (ln − − ln )2 (ln + − ln )2 = − (ln )−1 + (ln )−1 = − −1 + −1 = − 1 + 1 = (2 − 1) (2 + 1) = 2 − 1 2 + 1 18. 1 + tanh 1 − tanh = 1 + (sinh ) cosh 1 − (sinh ) cosh = cosh + sinh cosh − sinh = 12 ( + −) + 1 2( − −) 12 ( + −) − 1 2( − −) = − = 2 Or: Using the results of Exercises 9 and 10, cosh + sinh cosh − sinh = − = 2 19. By Exercise 9, (cosh + sinh) = () = = cosh + sinh . 20. coth = 1 tanh ⇒ coth = tanh 1 = 121 13 = 13 12. sech2 = 1 − tanh2 = 1 − 12 132 = 169 25 ⇒ sech = 13 5 [sech, like cosh, is positive]. cosh = 1 sech ⇒ cosh = 5113 = 13 5 . tanh = sinh cosh ⇒ sinh = tanh cosh ⇒ sinh = 12 13 · 13 5 = 12 5 . csch = 1 sinh ⇒ csch = 1215 = 12 5 . 21. sech = 1 cosh ⇒ sech = 513 = 35. cosh2 − sinh2 = 1 ⇒ sinh2 = cosh2 − 1 = 5 32 − 1 = 16 9 ⇒ sinh = 4 3 [because 0]. csch = 1 sinh ⇒ csch = 41 3 = 34. tanh = sinh cosh ⇒ tanh = 4 5 3 3 = 45. coth = 1 tanh ⇒ coth = 41 5 = 54. 22. (a) 23. (a) lim →∞ tanh = lim →∞ − − + − · − − = lim →∞ 1 − −2 1 + −2 = 1 − 0 1 + 0 = 1 (b) lim →−∞ tanh = lim →−∞ − − + − · = lim →−∞ 2 − 1 2 + 1 = 0 − 1 0 + 1 = −1 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.11 HYPERBOLIC FUNCTIONS ¤ 267 (c) lim →∞ sinh = lim →∞ − − 2 = ∞ (d) lim →−∞ sinh = lim →−∞ − − 2 = −∞ (e) lim →∞ sech = lim →∞ 2 + − = 0 (f ) lim →∞ coth = lim →∞ + − − − · − − = lim →∞ 1 + −2 1 − −2 = 1 + 0 1 − 0 = 1 [Or: Use part (a)] (g) lim →0+ coth = lim →0+ cosh sinh = ∞, since sinh → 0 through positive values and cosh → 1. (h) lim →0− coth = lim →0− cosh sinh = −∞, since sinh → 0 through negative values and cosh → 1. (i) lim →−∞ csch = lim →−∞ 2 − − = 0 (j) lim →∞ sinh = lim →∞ − − 2 = lim →∞ 1 − −2 2 = 1 − 0 2 = 1 2 24. (a) (cosh ) = 1 2( + −) = 1 2( − −) = sinh (b) (tanh ) = cosh sinh = cosh coshcosh −2sinh sinh = cosh2cosh −2sinh 2 = cosh 1 2 = sech2 (c) (csch ) = sinh 1 = −sinh cosh2 = −sinh 1 · cosh sinh = − csch coth (d) (sech ) = cosh 1 = −cosh sinh2 = −cosh 1 · cosh sinh = − sech tanh (e) (coth ) = cosh sinh = sinh sinhsinh −2cosh cosh = sinh2sinh −2cosh 2 = −sinh12 = − csch2 25. Let = sinh−1 . Then sinh = and, by Example 1(a), cosh2 − sinh2 = 1 ⇒ [with cosh 0] cosh =1 + sinh2 = √1 + 2. So by Exercise 9, = sinh + cosh = + √1 + 2 ⇒ = ln + √1 + 2 . 26. Let = cosh−1 . Then cosh = and ≥ 0, so sinh = cosh2 − 1 = √2 − 1. So, by Exercise 9, = cosh + sinh = + √2 − 1 ⇒ = ln + √2 − 1 . Another method: Write = cosh = 1 2 + − and solve a quadratic, as in Example 3. 27. (a) Let = tanh−1 . Then = tanh = sinh cosh = ( − −)2 ( + −)2 · = 2 − 1 2 + 1 ⇒ 2 + = 2 − 1 ⇒ 1 + = 2 − 2 ⇒ 1 + = 2(1 − ) ⇒ 2 = 1 + 1 − ⇒ 2 = ln1 + 1 − ⇒ = 1 2 ln1 + 1 − . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.268 ¤ CHAPTER 3 DIFFERENTIATION RULES (b) Let = tanh−1 . Then = tanh , so from Exercise 18 we have 2 = 1 + tanh 1 − tanh = 1 + 1 − ⇒ 2 = ln1 + 1 − ⇒ = 1 2 ln1 + 1 − . 28. (a) (i) = csch−1 ⇔ csch = ( 6= 0) (ii) We sketch the graph of csch−1 by reflecting the graph of csch (see Exercise 22) about the line = . (iii) Let = csch−1 . Then = csch = 2 − − ⇒ − − = 2 ⇒ ()2 − 2 − = 0 ⇒ = 1 ± √2 + 1 . But 0, so for 0, = 1 + √2 + 1 and for 0, = 1 − √2 + 1 . Thus, csch−1 = ln1 + √|2|+ 1. (b) (i) = sech−1 ⇔ sech = and 0 (ii) We sketch the graph of sech−1 by reflecting the graph of sech (see Exercise 22) about the line = . (iii) Let = sech−1 , so = sech = 2 + − ⇒ + − = 2 ⇒ ()2 − 2 + = 0 ⇔ = 1 ± √1 − 2 . But 0 ⇒ 1. This rules out the minus sign because 1 − √1 − 2 1 ⇔ 1 − √1 − 2 ⇔ 1 − √1 − 2 ⇔ 1 − 2 + 2 1 − 2 ⇔ 2 ⇔ 1, but = sech ≤ 1. Thus, = 1 + √1 − 2 ⇒ sech−1 = ln1 + √1 − 2 . (c) (i) = coth−1 ⇔ coth = (ii) We sketch the graph of coth−1 by reflecting the graph of coth (see Exercise 22) about the line = . (iii) Let = coth−1 . Then = coth = + − − − ⇒ − − = + − ⇒ ( − 1) = ( + 1)− ⇒ 2 = + 1 − 1 ⇒ 2 = ln + 1 − 1 ⇒ coth−1 = 1 2 ln + 1 − 1 29. (a) Let = cosh−1 . Then cosh = and ≥ 0 ⇒ sinh = 1 ⇒ = 1 sinh = 1 cosh2 − 1 = 1 √2 − 1 [since sinh ≥ 0 for ≥ 0]. Or: Use Formula 4. (b) Let = tanh−1 . Then tanh = ⇒ sech2 = 1 ⇒ = sech 1 2 = 1 − tanh 1 2 = 1 −12 . Or: Use Formula 5. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.11 HYPERBOLIC FUNCTIONS ¤ 269 (c) Let = csch−1 . Then csch = ⇒ − csch coth = 1 ⇒ = −csch 1coth . By Exercise 13, coth = ±csch2 + 1 = ±√2 + 1. If 0, then coth 0, so coth = √2 + 1. If 0, then coth 0, so coth = −√2 + 1. In either case we have = − 1 csch coth = − 1 || √2 + 1. (d) Let = sech−1 . Then sech = ⇒ − sech tanh = 1 ⇒ = − 1 sech tanh = − 1 sech 1 − sech2 = − 1 √1 − 2 . [Note that 0 and so tanh 0.] (e) Let = coth−1 . Then coth = ⇒ − csch2 = 1 ⇒ = −csch 12 = 1 − coth 1 2 = 1 −12 by Exercise 13. 30. () = cosh ⇒PR 0() = sinh + (cosh ) = (sinh + cosh ), or, using Exercise 9, () = 2. 31. () = tanh √ ⇒ 0() = sech2 √ √ = sech2 √ 2√1 = sech 2√2√ 32. () = sinh2 = (sinh )2 ⇒ 0() = 2(sinh )1 (sinh ) = 2 sinh cosh , or, using Exercise 15, sinh 2. 33. () = sinh(2) ⇒ 0() = cosh(2) (2) = 2 cosh(2) 34. () = ln(sinh ) ⇒ 0() = 1 sinh sinh = sinh 1 cosh = coth 35. () = sinh(ln ) ⇒ 0() = cosh(ln ) ln = 12ln + − ln 1 = 21 + 1 = 212 + 1 = 22+ 1 2 Or: () = sinh(ln ) = 1 2 (ln − − ln ) = 1 2 − 1 ⇒ 0() = 121 + 12 = 22+ 1 2 36. = sech (1 + ln sech ) ⇒PR 0 = sech (1 + ln sech ) + (1 + ln sech ) sech = sech −sech sech tanh + (1 + ln sech )(−sech tanh ) = −sech tanh [1 + (1 + ln sech )] = −sech tanh (2 + ln sech ) 37. = cosh 3 ⇒ 0 = cosh 3 · sinh 3 · 3 = 3cosh 3 sinh 3 38. () = 1 + sinh 1 − sinh QR ⇒ 0() = (1 − sinh ) cosh − (1 + sinh )(− cosh ) (1 − sinh )2 = cosh − sinh cosh + cosh + sinh cosh (1 − sinh )2 = 2 cosh (1 − sinh )2 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.270 ¤ CHAPTER 3 DIFFERENTIATION RULES 39. () = coth √2 + 1 ⇒PR 0() = − csch2 √2 + 1 1 2(2 + 1)−12 · 2 + coth √2 + 1 (1) = coth √2 + 1 − √22+ 1 csch2 √2 + 1 40. = sinh−1(tan ) ⇒ 0 = 1 + (tan 1 )2 (tan ) = √sec sec22 = ||sec sec2|| =| sec | 41. = cosh−1√ ⇒ 0 = (√1)2 − 1 (√ ) = √1− 1 2√1 = 2(1 − 1) 42. = tanh−1 + ln √1 − 2 = tanh−1 + 1 2 ln(1 − 2) ⇒ 0 = tanh−1 + 1 − 2 + 1 2 1 −12 (−2) = tanh−1 43. = sinh−1(3) − √9 + 2 ⇒ 0 = sinh−13 + 1 + ( 133)2 − 2 √9 + 2 2 = sinh−13 + √9 + 2 − √9 + 2 = sinh−1 3 44. = sech −1(−) ⇒ 0 = − 1 −1 − (−)2 (−) = −−√11− −2 (−−) = √1 −1−2 45. = coth−1(sec ) ⇒ 0 = 1 1 − (sec )2 (sec ) = sec 1 −sec tan 2 = 1 −sec (tan tan 2 + 1) = sec − tan tan 2 = − sec tan = − 1 cos sin cos = − 1 sin = − csc 46. 1 + tanh 1 − tanh = 1 + (sinh ) cosh 1 − (sinh ) cosh = cosh + sinh cosh − sinh = − [by Exercises 9 and 10] = 2, so 4 1 + tanh 1 − tanh = √4 2 = 2. Thus, 4 1 + tanh 1 − tanh = (2) = 122. 47. arctan(tanh ) = 1 + (tanh 1 )2 (tanh ) = 1 + tanh sech2 2 = 1 + (sinh 1 cosh 2 )2 cosh 2 = 1 cosh2 + sinh2 = 1 cosh 2 [by Exercise 16] = sech 2 48. (a) Let = 003291765. A graph of the central curve, = () = 21149 − 2096 cosh , is shown. (b) (0) = 21149 − 2096 cosh 0 = 21149 − 2096(1) = 19053 m (c) = 100 ⇒ 100 = 21149 − 2096 cosh ⇒ 2096 cosh = 11149 ⇒ cosh = 11149 2096 ⇒ = ± cosh−1 11149 2096 ⇒ = ± 1 cosh−1 11149 2096 ≈ ±7156 m. The points are approximately (±7156 100). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 3.11 HYPERBOLIC FUNCTIONS ¤ 271 (d) () = 21149 − 2096 cosh ⇒ 0() = −2096 sinh · . 0±1 cosh−1 111 2096 49 = −2096 sinh±1 cosh−1 111 2096 49 = −2096 sinh± cosh−1 111 2096 49 ≈ ∓36. So the slope at (7156 100) is about −36 and the slope at (−7156 100) is about 36. 49. As the depth of the water gets large, the fraction 2 gets large, and from Figure 3 or Exercise 23(a), tanh2 approaches 1. Thus, = 2 tanh2 ≈ 2 (1) = 2 . 50. For = cosh() with 0, we have the -intercept equal to . As increases, the graph flattens. 51. (a) = 20 cosh(20) − 15 ⇒ 0 = 20 sinh(20) · 20 1 = sinh(20). Since the right pole is positioned at = 7, we have 0(7) = sinh 20 7 ≈ 03572. (b) If is the angle between the tangent line and the -axis, then tan = slope of the line = sinh 20 7 , so = tan−1sinh 20 7 ≈ 0343 rad ≈ 1966◦. Thus, the angle between the line and the pole is = 90◦ − ≈ 7034◦. 52. We differentiate the function twice, then substitute into the differential equation: = cosh ⇒ = sinh = sinh ⇒ 22 = cosh = cosh . We evaluate the two sides separately: LHS = 2 2 = cosh and RHS = 1 + 2 = 1 + sinh2 = cosh , by the identity proved in Example 1(a). 53. (a) From Exercise 52, the shape of the cable is given by = () = cosh . The shape is symmetric about the -axis, so the lowest point is (0 (0)) = 0 and the poles are at = ±100. We want to find when the lowest point is 60 m, so = 60 ⇒ = 60 = (60 m)(2 kgm)(98 ms2) = 1176 kg-m s2 , or 1176 N (newtons). The height of each pole is (100) = cosh ·100 = 60 cosh100 60 ≈ 16450 m. (b) If the tension is doubled from to 2, then the low point is doubled since = 60 ⇒ 2 = 120. The height of the poles is now (100) = 2 cosh2·100 = 120 cosh100 120 ≈ 16413 m, just a slight decrease. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.272 ¤ CHAPTER 3 DIFFERENTIATION RULES 54. (a) lim →∞ () = lim →∞ tanh = lim →∞tanh = · 1 as → ∞→ ∞ , = (b) Belly-to-earth: = 98, = 0515, = 60, so the terminal velocity is 60(9 0515 8) ≈ 3379 ms. Feet-first: = 98, = 0067, = 60, so the terminal velocity is 60(9 0067 8) ≈ 9368 ms. 55. (a) = sinh + cosh ⇒ 0 = cosh + sinh ⇒ 00 = 2 sinh + 2 cosh = 2( sinh + cosh ) = 2 (b) From part (a), a solution of 00 = 9 is () = sinh 3 + cosh 3. So −4 = (0) = sinh 0 + cosh 0 = , so = −4. Now 0() = 3 cosh 3 − 12 sinh 3 ⇒ 6 = 0(0) = 3 ⇒ = 2, so = 2 sinh 3 − 4 cosh 3. 56. cosh = cosh[ln(sec + tan )] = 1 2ln(sec +tan ) + − ln(sec +tan ) = 12sec + tan + sec + tan 1 = 1 2 sec + tan + (sec + tan sec −)(sec tan− tan ) = 12sec + tan + sec sec 2 − − tan tan2 = 12 (sec + tan + sec − tan ) = sec 57. The tangent to = cosh has slope 1 when 0 = sinh = 1 ⇒ = sinh−1 1 = ln1 + √2 , by Equation 3. Since sinh = 1 and = cosh = 1 + sinh2 , we have cosh = √2. The point is ln1 + √2 , √2 . 58. () = tanh( sin ), where is a positive integer. Note that ( + 2) = (); that is, is periodic with period 2. Also, from Figure 3, −1 tanh 1, so we can choose a viewing rectangle of [0 2] × [−1 1]. From the graph, we see that () becomes more rectangular looking as increases. As becomes large, the graph of approaches the graph of = 1 on the intervals (2 (2 + 1)) and = −1 on the intervals ((2 − 1) 2). 59. If + − = cosh( + ) [or sinh( + )], then + − = 2 + ± −− = 2 ± −− = 2 ± 2 −−. Comparing coefficients of and −, we have = 2 (1) and = ± 2 − (2). We need to find and . Dividing equation (1) by equation (2) gives us = ±2 ⇒ () 2 = ln± ⇒ = 1 2 ln± . Solving equations (1) and (2) for gives us = 2 and = ± 2, so 2 = ± 2 ⇒ 2 = ±4 ⇒ = 2 √±. () If 0, we use the + sign and obtain a cosh function, whereas if 0, we use the − sign and obtain a sinh function. In summary, if and have the same sign, we have + − = 2 √ cosh + 1 2 ln , whereas, if and have the opposite sign, then + − = 2 √− sinh + 1 2 ln− . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 REVIEW ¤ 273 3 Review 1. True. This is the Sum Rule. 2. False. See the warning before the Product Rule. 3. True. This is the Chain Rule. 4. True. () = [()]12 = 12[()]−12 0() = 2 0(()) 5. False. (√ ) = 0(√ ) · 1 2−12 = 20(√√), which is not 20√(). 6. False. = 2 is a constant, so 0 = 0, not 2. 7. False. (10) = 10 ln 10, which is not equal to 10−1. 8. False. ln 10 is a constant, so its derivative, (ln 10), is 0, not 10 1 . 9. True. (tan2 ) = 2 tan sec2 , and (sec2 ) = 2 sec (sec tan ) = 2 tan sec2 . Or: (sec2 ) = (1 + tan2 ) = (tan2 ). 10. False. () = 2 + = 2 + for ≥ 0 or ≤ −1 and 2 + = −(2 + ) for −1 0. So 0() = 2 + 1 for 0 or −1 and 0() = −(2 + 1) for −1 0. But |2 + 1| = 2 + 1 for ≥ − 1 2 and |2 + 1| = −2 − 1 for − 1 2. 11. True. If () = + −1−1 + · · · + 1 + 0, then 0() = −1 + ( − 1)−1−2 + · · · + 1, which is a polynomial. 12. True. () = (6 − 4)5 is a polynomial of degree 30, so its 31st derivative, (31)(), is 0. 13. True. If () = () (), then 0() = ()0([)(−)] 2()0(), which is a quotient of polynomials, that is, a rational function. 14. False. A tangent line to the parabola = 2 has slope = 2, so at (−2 4) the slope of the tangent is 2(−2) = −4 and an equation of the tangent line is − 4 = −4( + 2). [The given equation, − 4 = 2( + 2), is not even linear!] 15. True. () = 5 ⇒ 0() = 54 ⇒ 0(2) = 5(2)4 = 80, and by the definition of the derivative, lim →2 () − (2) − 2 = 0(2) = 5(2)4 = 80. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.274 ¤ CHAPTER 3 DIFFERENTIATION RULES 1. = (2 + 3)4 ⇒ 0 = 4(2 + 3)3(2 + 32) = 4(2)3(1 + )3(2 + 3) = 47( + 1)3(3 + 2) 2. = √1 − √513 = −12 − −35 ⇒ 0 = −1 2−32 + 35−85 or 5√35 3 − 21√ or 10 1 −85(−5110 + 6) 3. = 2 −√+ 2 = 32 − 12 + 2−12 ⇒ 0 = 3212 − 12−12 − −32 = 32√ − 2√1 − √13 4. = tan 1 + cos ⇒ 0 = (1 + cos ) sec2 − tan(− sin ) (1 + cos )2 = (1 + cos ) sec2 + tan sin (1 + cos )2 5. = 2 sin ⇒ 0 = 2(cos ) + (sin )(2) = (cos + 2 sin ) 6. = cos−1 ⇒ 0 = −√1 1− 2 + (cos−1 )(1) = cos−1 − √1 − 2 7. = 4 − 1 4 + 1 ⇒ 0 = (4 + 1)4(43 + 1) − (42 − 1)43 = 43[(4 (+ 1) 4 + 1) − (24 − 1)] = (48+ 1) 3 2 8. () = ( sin ) ⇒ 0 + · 1 = cos + sin · 0 ⇒ 0 − sin · 0 = cos − ⇒ ( − sin )0 = cos − ⇒ 0 = cos − − sin 9. = ln( ln ) ⇒ 0 = 1 ln ( ln )0 = ln 1 · 1 + ln · 1 = 1 + ln ln Another method: = ln( ln ) = ln + ln ln ⇒ 0 = 1 + 1 ln · 1 = ln + 1 ln 10. = cos ⇒ 0 = (cos )0 + cos ()0 = (− sin · ) + cos ( · ) = ( cos − sin) 11. = √ cos √ ⇒ 0 = √ cos √ 0 + cos √ √ 0 = √ − sin √ 1 2−12 + cos √ 1 2−12 = 12 −12 −√ sin √ + cos √ = cos √ −2 √√ sin √ 12. = (arcsin 2)2 ⇒ 0 = 2(arcsin 2) · (arcsin 2)0 = 2 arcsin 2 · 1 −1(2)2 · 2 = 4 arcsin 2 √1 − 42 13. = 1 2 ⇒ 0 = 2(1)(0−2)21 20 = 2(1)(−1 42) − 1(2) = −1(1 + 2 4 ) 14. = ln sec ⇒ 0 = 1 sec (sec ) = sec 1 (sec tan ) = tan °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 REVIEW ¤ 275 15. ( + cos ) = (2) ⇒ 0 + (− sin · 0) + cos · 1 = 20 + · 2 ⇒ 0 − sin · 0 − 20 = 2 − cos ⇒ (1 − sin − 2)0 = 2 − cos ⇒ 0 = 2 − cos 1 − sin − 2 16. = 2 +−1+ 14 ⇒ 0 = 4 2 +−1+ 13 2 +−1+ 1 = 42 +−1+ 13 (2 + + 1)(1) (2 +− + 1) ( −21)(2 + 1) = 4( − 1)3 (2 + + 1)3 2 + + 1 − 22 + + 1 (2 + + 1)2 = 4( − 1)3(−2 + 2 + 2) (2 + + 1)5 17. = √arctan ⇒ 0 = 1 2 (arctan )−12 (arctan ) = 2 √arctan1 (1 + 2) 18. = cot(csc ) ⇒ 0 = − csc2(csc ) (csc ) = − csc2(csc ) · (− csc cot ) = csc2(csc ) csc cot 19. = tan1 + 2 ⇒ 0 = sec21 + 2 1 + 2 = sec21 + 2 · (1 +(1 + 2)(1) 2−)2(2) = (1 + 1 −22)2 sec21 + 2 20. = sec ⇒ 0 = sec ( sec ) = sec ( sec tan + sec · 1) = sec sec ( tan + 1) 21. = 3 ln ⇒ 0 = 3 ln (ln 3) ( ln ) = 3 ln (ln 3) · 1 + ln · 1 = 3 ln (ln 3)(1 + ln ) 22. = sec(1 + 2) ⇒ 0 = 2 sec(1 + 2) tan(1 + 2) 23. = (1 − −1)−1 ⇒ 0 = −1(1 − −1)−2[−(−1−2)] = −(1 − 1)−2−2 = −(( − 1))−2−2 = −( − 1)−2 24. = 1 3 + √ = + √ −13 ⇒ 0 = − 1 3 + √ −431 + 2 √1 25. sin() = 2 − ⇒ cos()(0 + · 1) = 2 − 0 ⇒ cos()0 + 0 = 2 − cos() ⇒ 0[ cos() + 1] = 2 − cos() ⇒ 0 = 2 − cos() cos() + 1 26. = sin√ ⇒ 0 = 1 2sin√ −12cos√ 2 √1 = 4 cos sin √√ 27. = log5(1 + 2) ⇒ 0 = 1 (1 + 2) ln 5 (1 + 2) = (1 + 22) ln 5 28. = (cos ) ⇒ ln = ln(cos ) = ln cos ⇒ 0 = · 1 cos · (− sin ) + ln cos · 1 ⇒ 0 = (cos )(ln cos − tan ) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.276 ¤ CHAPTER 3 DIFFERENTIATION RULES 29. = ln sin − 1 2 sin2 ⇒ 0 = 1 sin · cos − 1 2 · 2 sin · cos = cot − sin cos 30. = (2 + 1)4 (2 + 1)3(3 − 1)5 ⇒ ln = ln (2 + 1)4 (2 + 1)3(3 − 1)5 = ln(2 + 1)4 − ln[(2 + 1)3(3 − 1)5] = 4 ln(2 + 1) − [ln(2 + 1)3 + ln(3 − 1)5] = 4 ln(2 + 1) − 3 ln(2 + 1) − 5 ln(3 − 1) ⇒ 0 = 4 · 1 2 + 1 · 2 − 3 · 21+ 1 · 2 − 5 · 31− 1 · 3 ⇒ 0 = (2 + 1) (2 3+ 1) (34− 1)5 28+ 1 − 26+ 1 − 315 − 1. [The answer could be simplified to 0 = −(2 + 56 + 9)(2 + 1)3 (2 + 1)4(3 − 1)6 , but this is unnecessary.] 31. = tan−1(4) ⇒ 0 = · 1 1 + (4)2 · 4 + tan−1(4) · 1 = 1 + 16 4 2 + tan−1(4) 32. = cos + cos( ) ⇒ 0 = cos (− sin ) + [− sin( ) · ] = − sin cos − sin( ) 33. = ln |sec 5 + tan 5| ⇒ 0 = 1 sec 5 + tan 5 (sec 5 tan 5 · 5 + sec2 5 · 5) = 5 sec 5 (tan 5 + sec 5) sec 5 + tan 5 = 5 sec 5 34. = 10 tan ⇒ 0 = 10 tan · ln 10 · sec2 · = (ln 10)10 tan sec2 35. = cot(32 + 5) ⇒ 0 = − csc2(32 + 5)(6) = −6 csc2(32 + 5) 36. = ln(4) ⇒ 0 = 1 2 [ ln(4)]−12 [ ln(4)] = 2 1ln(4) · 1 · ln(4) + · 14 · 43 = 2 1ln(4) · [ln(4) + 4] = 2ln( 4ln( ) + 4 4) Or: Since y is only defined for 0, we can write = √ · 4 ln = 2 √ ln . Then 0 = 2 · 1 2 √ ln · 1 · ln + · 1 = ln √ ln + 1 . This agrees with our first answer since ln(4) + 4 2 ln(4) = 4 ln + 4 2 √ · 4 ln = 4(ln + 1) 2 · 2 √ ln = ln + 1 √ ln . 37. = sintan √1 + 3 ⇒ 0 = costan √1 + 3 sec2 √1 + 3 322 √1 + 3 38. = arctanarcsin √ ⇒ 0 = 1 1 + arcsin √ 2 · 1 √1 − · 1 2 √ 39. = tan2(sin ) = [tan(sin )]2 ⇒ 0 = 2[tan(sin )] · sec2(sin ) · cos 40. = − 1 ⇒ 0 + = 0 ⇒ = 0 − 0 ⇒ 0 = (1 − ) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 REVIEW ¤ 277 41. = √ + 1 (2 − )5 ( + 3)7 ⇒ ln = 1 2 ln( + 1) + 5 ln(2 − ) − 7 ln( + 3) ⇒ 0 = 2(1+ 1) + 2−−5 − + 3 7 ⇒ 0 = √ + 1 (2 − )5 ( + 3)7 2(1+ 1) − 2 −5 − + 3 7 or 0 = (2 −2√)4(3+ 1 ( 2 −55 + 3) −8 52). 42. = ( + )4 4 + 4 ⇒ 0 = (4 + 4)(4)((+4 +)34−)2( + )4(43) = 4( +(4)3+(44−)2 3) 43. = sinh(2) ⇒ 0 = cosh(2) · 2 + sinh(2) · 1 = 22 cosh(2) + sinh(2) 44. = (sin ) ⇒ 0 = (cos − sin )2 45. = ln(cosh 3) ⇒ 0 = (1 cosh 3)(sinh 3)(3) = 3 tanh 3 46. = ln 2 − 4 2 + 5 = ln 2 − 4 − ln |2 + 5| ⇒ 0 = 2 2 − 4 − 2 2 + 5 or 2( + 1)( + 4) ( + 2)( − 2)(2 + 5) 47. = cosh−1(sinh ) ⇒ 0 = (sinh1)2 − 1 · cosh = sinh cosh 2 − 1 48. = tanh−1√ ⇒ 0 = tanh−1√ + 1 1 − √ 2 1 2 √ = tanh−1√ + √ 2(1 − ) 49. = cos√tan 3 ⇒ 0 = − sin√tan 3 · √tan 3 0 = − sin√tan 3 √tan 3 · 1 2(tan 3)−12 · sec2(3) · 3 = −3 sin√tan 3 √tan 3 sec2(3) 2 √tan 3 50. = sin2cos √sin = sincos √sin 2 ⇒ 0 = 2sincos √sin sincos √sin 0 = 2 sincos √sin coscos √sin cos √sin 0 = 2 sincos √sin coscos √sin − sin √sin √sin 0 = −2 sincos √sin coscos √sin sin √sin · 1 2(sin )−12(sin )0 = − sincos √sin coscos √sin sin √sin √sin · cos · = − sincos √sin coscos √sin sin √sin cos √sin 51. () = √4 + 1 ⇒ 0() = 1 2(4 + 1)−12 · 4 = 2(4 + 1)−12 ⇒ 00() = 2(− 1 2)(4 + 1)−32 · 4 = −4(4 + 1)32, so 00(2) = −4932 = − 27 4 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.278 ¤ CHAPTER 3 DIFFERENTIATION RULES 52. () = sin ⇒ 0() = cos + sin · 1 ⇒ 00() = (− sin ) + cos · 1 + cos = 2 cos − sin , so 00(6) = 2 cos(6) − (6) sin(6) = 2 √32 − (6)(12) = √3 − 12. 53. 6 + 6 = 1 ⇒ 65 + 650 = 0 ⇒ 0 = −55 ⇒ 00 = −5(54) − 5(540) (5)2 = − 544 − (−55) 10 = − 54 (6 + 6)5 6 = − 54 11 54. () = (2 − )−1 ⇒ 0() = (2 − )−2 ⇒ 00() = 2(2 − )−3 ⇒ 000() = 2 · 3(2 − )−4 ⇒ (4)() = 2 · 3 · 4(2 − )−5. In general, ()() = 2 · 3 · 4 · · · · · (2 − )−(+1) = ! (2 − )(+1) . 55. We first show it is true for = 1: () = ⇒ 0() = + = ( + 1). We now assume it is true for = : ()() = ( + ). With this assumption, we must show it is true for = + 1: (+1)() = ()() = [( + )] = ( + ) + = [( + ) + 1] = [ + ( + 1)]. Therefore, ()() = ( + ) by mathematical induction. 56. lim →0 3 tan3 2 = lim →0 3sin cos 3 322 = lim →0 cos3 2 · 1 8sin3 2 (2)3 = lim →0 cos3 2 8lim →0 sin 2 2 3 = 1 8 · 13 = 1 8 57. = 4 sin2 ⇒ 0 = 4 · 2 sin cos . At 6 1, 0 = 8 · 1 2 · √23 = 2 √3, so an equation of the tangent line is − 1 = 2 √3 − 6 , or = 2 √3 + 1 − √33. 58. = 2 − 1 2 + 1 ⇒ 0 = (2 + 1)(2(2) −+ 1) (22 − 1)(2) = (24+ 1) 2 . At (0 −1), 0 = 0, so an equation of the tangent line is + 1 = 0( − 0), or = −1. 59. = √1 + 4 sin ⇒ 0 = 1 2(1 + 4 sin )−12 · 4 cos = √1 + 4 sin 2 cos . At (0 1), 0 = √21 = 2, so an equation of the tangent line is − 1 = 2( − 0), or = 2 + 1. 60. 2 + 4 + 2 = 13 ⇒ 2 + 4(0 + · 1) + 20 = 0 ⇒ + 20 + 2 + 0 = 0 ⇒ 20 + 0 = − − 2 ⇒ 0(2 + ) = − − 2 ⇒ 0 = − − 2 2 + . At (2 1), 0 = −2 − 2 4 + 1 = − 4 5 , so an equation of the tangent line is − 1 = − 4 5( − 2), or = − 4 5 + 13 5 . The slope of the normal line is 5 4, so an equation of the normal line is − 1 = 5 4( − 2), or = 5 4 − 3 2. 61. = (2 + )− ⇒ 0 = (2 + )(−−) + − · 1 = −[−(2 + ) + 1] = −(− − 1). At (0 2), 0 = 1(−1) = −1, so an equation of the tangent line is − 2 = −1( − 0), or = − + 2. The slope of the normal line is 1, so an equation of the normal line is − 2 = 1( − 0), or = + 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 REVIEW ¤ 279 62. () = sin ⇒ 0() = [sin (cos )] + sin (1) = sin ( cos + 1). As a check on our work, we notice from the graphs that 0() 0 when is increasing. Also, we see in the larger viewing rectangle a certain similarity in the graphs of and 0: the sizes of the oscillations of and 0 are linked. 63. (a) () = √5 − ⇒ 0() = 21(5 − )−12(−1) + √5 − = 2 √−5− + √5 − · 22 √√5 5 − − = 2 √−5− + 22(5 √5−−) = − + 10 − 2 2 √5 − = 10 − 3 2 √5 − (b) At (1 2): 0(1) = 7 4 . So an equation of the tangent line is − 2 = 7 4( − 1) or = 7 4 + 1 4 . At (4 4): 0(4) = − 2 2 = −1. So an equation of the tangent line is − 4 = −1( − 4) or = − + 8. (c) (d) The graphs look reasonable, since 0 is positive where has tangents with positive slope, and 0 is negative where has tangents with negative slope. 64. (a) () = 4 − tan ⇒ 0() = 4 − sec2 ⇒ 00() = −2 sec (sec tan ) = −2 sec2 tan . (b) We can see that our answers are reasonable, since the graph of 0 is 0 where has a horizontal tangent, and the graph of 0 is positive where has tangents with positive slope and negative where has tangents with negative slope. The same correspondence holds between the graphs of 0 and 00. 65. = sin + cos ⇒ 0 = cos − sin = 0 ⇔ cos = sin and 0 ≤ ≤ 2 ⇔ = 4 or 54 , so the points are 4 √2 and 54 −√2 . 66. 2 + 22 = 1 ⇒ 2 + 40 = 0 ⇒ 0 = −(2) = 1 ⇔ = −2. Since the points lie on the ellipse, we have (−2)2 + 22 = 1 ⇒ 62 = 1 ⇒ = ± √16 . The points are − √26 √16 and √26 − √16. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.280 ¤ CHAPTER 3 DIFFERENTIATION RULES 67. () = ( − )( − )( − ) ⇒ 0() = ( − )( − ) + ( − )( − ) + ( − )( − ). So 0() () = ( − )( − ) + ( − )( − ) + ( − )( − ) ( − )( − )( − ) = 1 − + 1 − + 1 − . Or: () = ( − )( − )( − ) ⇒ ln |()| = ln | − | + ln | − | + ln | − | ⇒ 0() () = 1 − + 1 − + 1 − 68. (a) cos 2 = cos2 − sin2 ⇒ −2 sin 2 = −2 cos sin − 2 sin cos ⇔ sin 2 = 2 sin cos (b) sin( + ) = sin cos + cos sin ⇒ cos( + ) = cos cos − sin sin . 69. (a) () = () + () ⇒ 0() = 0() + 0() ⇒ 0(1) = 0(1) + 0(1) = 3 + 1 = 4 (b) () = () () ⇒ 0() = () 0() + () 0() ⇒ 0(2) = (2) 0(2) + (2) 0(2) = 1(4) + 1(2) = 4 + 2 = 6 (c) () = () () ⇒ 0() = () 0([)(−)] 2() 0() ⇒ 0(1) = (1) 0(1) − (1) 0(1) [(1)]2 = 3(3) − 2(1) 32 = 9 − 2 9 = 7 9 (d) () = (()) ⇒ 0() = 0(()) 0() ⇒ 0(2) = 0((2)) 0(2) = 0(1) · 4 = 3 · 4 = 12 70. (a) () = () () ⇒ 0() = () 0() + () 0() ⇒ 0(2) = (2) 0(2) + (2) 0(2) = (1) 6 3− −0 0 + (4) 0 3− −3 0 = (1)(2) + (4)(−1) = 2 − 4 = −2 (b) () = () () ⇒ 0() = () 0([)(−)] 2() 0() ⇒ 0(2) = (2) 0(2) − (2) 0(2) [(2)]2 = (4)(−1) − (1)(2) 42 = −6 16 = − 3 8 (c) () = (()) ⇒ 0() = 0(())0() ⇒ 0(2) = 0((2))0(2) = 0(4)0(2) = 6 5− −0 3(2) = (3)(2) = 6 71. () = 2() ⇒ 0() = 20() + ()(2) = [0() + 2()] 72. () = (2) ⇒ 0() = 0(2)(2) = 20(2) 73. () = [ ()]2 ⇒ 0() = 2[ ()] · 0() = 2() 0() 74. () = (()) ⇒ 0() = 0(()) 0() 75. () = () ⇒ 0() = 0() 76. () = () ⇒ 0() = ()0() 77. () = ln |()| ⇒ 0() = 1 ()0() = 0(()) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 REVIEW ¤ 281 78. () = (ln ) ⇒ 0() = 0(ln ) · 1 = 0(ln ) 79. () = () () () + () ⇒ 0() = [() + ()] [() 0() + () 0()] − () () [ 0() + 0()] [() + ()]2 = [()]2 0() + () () 0() + () () 0() + [ ()]2 0() − () () 0() − () () 0() [() + ()]2 = 0() [ ()]2 + 0() [()]2 [() + ()]2 80. () = (()) ⇒ 0() = 20()(()) −() [ ()(0)] (2) = 0(2[)(()] )3−2()()0() 81. Using the Chain Rule repeatedly, () = ((sin 4)) ⇒ 0() = 0((sin 4)) · ((sin 4)) = 0((sin 4)) · 0(sin 4) · (sin 4) = 0((sin 4))0(sin 4)(cos 4)(4). 82. (a) (b) The average rate of change is larger on [2 3]. (c) The instantaneous rate of change (the slope of the tangent) is larger at = 2. (d) () = − 2 sin ⇒ 0() = 1 − 2 cos , so 0(2) = 1 − 2 cos 2 ≈ 18323 and 0(5) = 1 − 2 cos 5 ≈ 04327. So 0(2) 0(5), as predicted in part (c). 83. = [ln( + 4)]2 ⇒ 0 = 2[ln( + 4)]1 · 1 + 4 · 1 = 2 ln( + 4 + 4) and 0 = 0 ⇔ ln( + 4) = 0 ⇔ + 4 = 0 ⇒ + 4 = 1 ⇔ = −3, so the tangent is horizontal at the point (−3 0). 84. (a) The line − 4 = 1 has slope 1 4. A tangent to = has slope 1 4 when 0 = = 1 4 ⇒ = ln 1 4 = − ln 4. Since = , the -coordinate is 1 4 and the point of tangency is − ln 4 1 4. Thus, an equation of the tangent line is − 1 4 = 1 4( + ln 4) or = 1 4 + 1 4(ln 4 + 1). (b) The slope of the tangent at the point ( ) is = = . Thus, an equation of the tangent line is − = ( − ). We substitute = 0, = 0 into this equation, since we want the line to pass through the origin: 0 − = (0 − ) ⇔ − = (−) ⇔ = 1. So an equation of the tangent line at the point ( ) = (1 ) is − = ( − 1) or = . 85. = () = 2 + + ⇒ 0() = 2 + . We know that 0(−1) = 6 and 0(5) = −2, so −2 + = 6 and 10 + = −2. Subtracting the first equation from the second gives 12 = −8 ⇒ = − 2 3. Substituting − 2 3 for in the first equation gives = 14 3 . Now (1) = 4 ⇒ 4 = + + , so = 4 + 2 3 − 14 3 = 0 and hence, () = − 2 32 + 14 3 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.282 ¤ CHAPTER 3 DIFFERENTIATION RULES 86. (a) lim →∞ () = lim →∞ [(− − −)] = lim →∞ (− − −) = (0 − 0) = 0 because − → −∞ and − → −∞ as → ∞. (b) () = (− − −) ⇒ 0() = (−(−) − −(−)) = (−− + −) (c) 0() = 0 ⇔ − = − ⇔ = (−+) ⇔ ln = ( − ) ⇔ = ln() − 87. () = − cos( + ) ⇒ () = 0() = {− [− sin( + )] + cos( + )(−−)} = −− [ sin( + ) + cos( + )] ⇒ () = 0() = −{−[2 cos( + ) − sin( + )] + [ sin( + ) + cos( + )](−−)} = −−[2 cos( + ) − sin( + ) − sin( + ) − 2 cos( + )] = −−[(2 − 2) cos( + ) − 2 sin( + )] = −[(2 − 2) cos( + ) + 2 sin( + )] 88. (a) = √2 + 2 2 ⇒ () = 0 = 12 √2 + 2 2 22 = 2√2 + 2 2 ⇒ () = 0() = 2 √2 + 2 2 − 22√2 + 2 2 2 + 2 2 = 22 (2 + 2 2)32 (b) () 0 for 0, so the particle always moves in the positive direction. 89. (a) = 3 − 12 + 3 ⇒ () = 0 = 32 − 12 ⇒ () = 0() = 6 (b) () = 3(2 − 4) 0 when 2, so it moves upward when 2 and downward when 0 ≤ 2. (c) Distance upward = (3) − (2) = −6 − (−13) = 7, Distance downward = (0) − (2) = 3 − (−13) = 16. Total distance = 7 + 16 = 23. (d) (e) The particle is speeding up when and have the same sign, that is, when 2. The particle is slowing down when and have opposite signs; that is, when 0 2. 90. (a) = 1 32 ⇒ = 1 32 [ constant] (b) = 1 32 ⇒ = 2 3 [ constant] 91. The linear density is the rate of change of mass with respect to length . = 1 + √ = + 32 ⇒ = = 1 + 3 2√, so the linear density when = 4 is 1 + 3 2√4 = 4 kgm. 92. (a) () = 920 + 2 − 0022 + 0000073 ⇒ 0() = 2 − 004 + 0000212 (b) 0(100) = 2 − 4 + 21 = $010unit. This value represents the rate at which costs are increasing as the hundredth unit is produced, and is the approximate cost of producing the 101st unit. (c) The cost of producing the 101st item is (101) − (100) = 99010107 − 990 = $010107, slightly larger than 0(100). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 REVIEW ¤ 283 93. (a) () = (0) = 200 ⇒ (05) = 20005 = 360 ⇒ 05 = 18 ⇒ 05 = ln 18 ⇒ = 2 ln 18 = ln(18)2 = ln 324 ⇒ () = 200(ln 324) = 200(324) (b) (4) = 200(324)4 ≈ 22,040 bacteria (c) 0() = 200(324) · ln 324, so 0(4) = 200(324)4 · ln 324 ≈ 25,910 bacteria per hour (d) 200(324) = 10,000 ⇒ (324) = 50 ⇒ ln 324 = ln 50 ⇒ = ln 50 ln 324 ≈ 333 hours 94. (a) If () is the mass remaining after years, then () = (0) = 100. (524) = 100524 = 1 2 · 100 ⇒ 524 = 1 2 ⇒ 524 = − ln 2 ⇒ = − 5124 ln 2 ⇒ () = 100−(ln 2)524 = 100 · 2−524. Thus, (20) = 100 · 2−20524 ≈ 71 mg. (b) 100 · 2−524 = 1 ⇒ 2−524 = 1 100 ⇒ − 524 ln 2 = ln 100 1 ⇒ = 524 ln 100 ln 2 ≈ 348 years 95. (a) 0() = −() ⇒ () = (0)− by Theorem 3.8.2. But (0) = 0, so () = 0−. (b) (30) = 1 20 since the concentration is reduced by half. Thus, 1 20 = 0−30 ⇒ ln 1 2 = −30 ⇒ = − 1 30 ln 1 2 = 30 1 ln 2. Since 10% of the original concentration remains if 90% is eliminated, we want the value of such that () = 10 1 0. Therefore, 10 1 0 = 0−(ln 2)30 ⇒ ln 01 = −(ln 2)30 ⇒ = − ln 2 30 ln 01 ≈ 100 h. 96. (a) If = − 20, (0) = 80 ⇒ (0) = 80 − 20 = 60, and the initial-value problem is = with (0) = 60. So the solution is () = 60. Now (05) = 60(05) = 60 − 20 ⇒ 05 = 40 60 = 2 3 ⇒ = 2 ln 2 3 = ln 4 9, so () = 60(ln 49) = 60( 4 9). Thus, (1) = 60( 4 9)1 = 80 3 = 26 2 3 ◦C and (1) = 46 2 3 ◦C. (b) () = 40 ⇒ () = 20. () = 6049 = 20 ⇒ 4 9 = 13 ⇒ ln 49 = ln 13 ⇒ = ln ln 1 3 4 9 ≈ 135 h or 813 min. 97. If = edge length, then = 3 ⇒ = 32 = 10 ⇒ = 10(32) and = 62 ⇒ = (12) = 12[10(32)] = 40. When = 30, = 40 30 = 4 3 cm2min. 98. Given = 2, find when = 5. = 1 32 and, from similar triangles, = 3 10 ⇒ = 3 310 2 = 100 3 3, so 2 = = 9 100 2 ⇒ = 200 92 = 200 9 (5)2 = 8 9 cms when = 5. 99. Given = 5 and = 15, find . 2 = 2 + 2 ⇒ 2 = 2 + 2 ⇒ = 1(15 + 5). When = 3, = 45 + 3(5) = 60 and = 15(3) = 45 ⇒ = √452 + 602 = 75, so = 1 75[15(45) + 5(60)] = 13 fts. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.284 ¤ CHAPTER 3 DIFFERENTIATION RULES 100. We are given = 30 fts. By similar triangles, = 4 √241 ⇒ = 4 √241, so = 4 √241 = 120 √241 ≈ 77 fts. 101. We are given = −025 radh. tan = 400 ⇒ = 400 cot ⇒ = −400 csc2 . When = 6 , = −400(2)2(−025) = 400 fth. 102. (a) () = √25 − 2 ⇒ 0() = −2 2 √25 − 2 = −(25 − 2)−12. So the linear approximation to () near 3 is () ≈ (3) + 0(3)( − 3) = 4 − 3 4( − 3). (b) (c) For the required accuracy, we want √25 − 2 − 01 4 − 3 4( − 3) and 4 − 3 4( − 3) √25 − 2 + 01. From the graph, it appears that these both hold for 224 366. 103. (a) () = √3 1 + 3 = (1 + 3)13 ⇒ 0() = (1 + 3)−23, so the linearization of at = 0 is () = (0) + 0(0)( − 0) = 113 + 1−23 = 1 + . Thus, √3 1 + 3 ≈ 1 + ⇒ √3 103 = 3 1 + 3(001) ≈ 1 + (001) = 101. (b) The linear approximation is √3 1 + 3 ≈ 1 + , so for the required accuracy we want √3 1 + 3 − 01 1 + √3 1 + 3 + 01. From the graph, it appears that this is true when −0235 0401. 104. = 3 − 22 + 1 ⇒ = (32 − 4) . When = 2 and = 02, = 3(2)2 − 4(2)(02) = 08. 105. = 2 + 1 2 1 22 = 1 + 8 2 ⇒ = 2 + 4 . When = 60 and = 01, = 2 + 4 60(01) = 12 + 32, so the maximum error is approximately 12 + 32 ≈ 167 cm2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 REVIEW ¤ 285 106. lim →1 17 − 1 − 1 = 17 = 1 = 17(1)16 = 17 107. lim →0 √4 16 + − 2 = √4 = 16 = 1 4−34 = 16 = 4√4116 3 = 32 1 108. lim →3 cos − 05 − 3 = cos = 3 = − sin 3 = −√23 109. lim →0 √1 + tan − √1 + sin 3 = lim →0 √1 + tan − √1 + sin √1 + tan + √1 + sin 3 √1 + tan + √1 + sin = lim →0 (1 + tan ) − (1 + sin ) 3√1 + tan + √1 + sin = lim →0 3√1 + tan sin (1cos + √ 1 + sin − 1) · cos cos = lim →0 sin (1 − cos ) 3√1 + tan + √1 + sin cos · 1 + cos 1 + cos = lim →0 sin · sin2 3√1 + tan + √1 + sin cos (1 + cos ) = lim →0 sin3 lim →0 √1 + tan + √1 + sin 1 cos (1 + cos ) = 13 · √1 + √1 1· 1 · (1 + 1) = 14 110. Differentiating the first given equation implicitly with respect to and using the Chain Rule, we obtain (()) = ⇒ 0(()) 0() = 1 ⇒ 0() = 1 0(()). Using the second given equation to expand the denominator of this expression gives 0() = 1 1 + [(())]2 . But the first given equation states that (()) = , so 0() = 1 +12 . 111. [(2)] = 2 ⇒ 0(2) · 2 = 2 ⇒ 0(2) = 1 22. Let = 2. Then 0() = 1 2 1 22 = 1 82, so 0() = 1 82. 112. Let ( ) be on the curve, that is, 23 + 23 = 23. Now 23 + 23 = 23 ⇒ 2 3−13 + 2 3−13 = 0, so = − 13 13 = − 13, so at ( ) the slope of the tangent line is −()13 and an equation of the tangent line is − = −()13( − ) or = −()13 + ( + 2313). Setting = 0, we find that the -intercept is 1323 + = 13(23 + 23) = 1323 and setting = 0 we find that the -intercept is + 2313 = 13(23 + 23) = 1323. So the length of the tangent line between these two points is (1323)2 + (1323)2 = √2343 + 2343 = (23 + 23)43 = √2343 = √2 = = constant °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.286 ¤ CHAPTER 3 DIFFERENTIATION RULES °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.PROBLEMS PLUS 1. Let be the -coordinate of . Since the derivative of = 1 − 2 is 0 = −2, the slope at is −2. But since the triangle is equilateral, = √31, so the slope at is −√3. Therefore, we must have that −2 = −√3 ⇒ = √23. Thus, the point has coordinates √23 1 − √232 = √23 1 4 and by symmetry, has coordinates − √23 1 4. 2. = 3 − 3 + 4 ⇒ 0 = 32 − 3, and = 3(2 − ) ⇒ 0 = 6 − 3. The slopes of the tangents of the two curves are equal when 32 − 3 = 6 − 3; that is, when = 0 or 2. At = 0, both tangents have slope −3, but the curves do not intersect. At = 2, both tangents have slope 9 and the curves intersect at (2 6). So there is a common tangent line at (2 6), = 9 − 12. 3. We must show that (in the figure) is halfway between and , that is, = ( + )2. For the parabola = 2 + + , the slope of the tangent line is given by 0 = 2 + . An equation of the tangent line at = is − (2 + + ) = (2 + )( − ). Solving for gives us = (2 + ) − 22 − + (2 + + ) or = (2 + ) + − 2 (1) Similarly, an equation of the tangent line at = is = (2 + ) + − 2 (2) We can eliminate and solve for by subtracting equation (1) from equation (2). [(2 + ) − (2 + )] − 2 + 2 = 0 (2 − 2) = 2 − 2 2( − ) = (2 − 2) = ( + )( − ) 2( − ) = + 2 Thus, the -coordinate of the point of intersection of the two tangent lines, namely , is ( + )2. 4. We could differentiate and then simplify or we can simplify and then differentiate. The latter seems to be the simpler method. sin2 1 + cot + cos2 1 + tan = sin2 1 + cos sin · sin sin + cos2 1 + sin cos · cos cos = sin3 sin + cos + cos3 cos + sin = sin3 + cos3 sin + cos [factor sum of cubes] = (sin + cos )(sin2 − sin cos + cos2 ) sin + cos = sin2 − sin cos + cos2 = 1 − sin cos = 1 − 1 2(2 sin cos ) = 1 − 1 2 sin 2 Thus, 1 + cot sin2 + 1 + tan cos2 = 1 − 1 2 sin 2 = − 1 2 cos 2 · 2 = − cos 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. 287 NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.288 ¤ CHAPTER 3 PROBLEMS PLUS 5. Using 0() = lim → () − () − , we recognize the given expression, () = lim → sec − sec − , as 0() with () = sec . Now 0( 4 ) = 00( 4 ), so we will find 00(). 0() = sec tan ⇒ 00() = sec sec2 + tan sec tan = sec (sec2 + tan2 ), so 00( 4 ) = √2(√22 + 12) = √2(2 + 1) = 3√2. 6. Using 0(0) = lim →0 () − (0) − 0 , we see that for the given equation, lim →0 √3 + − 2 = 5 12 , we have () = √3 + , (0) = 2, and 0(0) = 12 5 . Now (0) = 2 ⇔ √3 = 2 ⇔ = 8. Also 0() = 1 3( + )−23 · , so 0(0) = 12 5 ⇔ 1 3(8)−23 · = 12 5 ⇔ 1 3( 1 4) = 12 5 ⇔ = 5. 7. Let = tan−1 . Then tan = , so from the triangle we see that sin(tan−1 ) = sin = √1 + 2 Using this fact we have that sin(tan−1(sinh )) = 1 + sinh sinh 2 = cosh sinh = tanh . Hence, sin−1(tanh ) = sin−1(sin(tan−1(sinh ))) = tan−1(sinh ). 8. We find the equation of the parabola by substituting the point (−100 100), at which the car is situated, into the general equation = 2: 100 = (−100)2 ⇒ = 100 1 . Now we find the equation of a tangent to the parabola at the point (0 0). We can show that 0 = (2) = 100 1 (2) = 50 1 , so an equation of the tangent is − 0 = 50 1 0( − 0). Since the point (0 0) is on the parabola, we must have 0 = 100 1 2 0, so our equation of the tangent can be simplified to = 100 1 2 0 + 50 1 0( − 0). We want the statue to be located on the tangent line, so we substitute its coordinates (100 50) into this equation: 50 = 100 1 2 0 + 50 1 0(100 − 0) ⇒ 2 0 − 2000 + 5000 = 0 ⇒ 0 = 1 2200 ± 2002 − 4(5000) ⇒ 0 = 100 ± 50 √2. But 0 100, so the car’s headlights illuminate the statue when it is located at the point 100 − 50 √2 150 − 100 √2 ≈ (293 86), that is, about 293 m east and 86 m north of the origin. 9. We use mathematical induction. Let be the statement that (sin4 + cos4 ) = 4−1 cos(4 + 2). 1 is true because (sin4 + cos4 ) = 4 sin3 cos − 4 cos3 sin = 4 sin cos sin2 − cos2 = −4 sin cos cos 2 = −2 sin 2 cos 2 = − sin 4 = sin(−4) = cos 2 − (−4) = cos 2 + 4 = 4−1 cos4 + 2 when = 1 [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 PROBLEMS PLUS ¤ 289 Now assume is true, that is, sin4 + cos4 = 4−1 cos4 + 2 . Then +1 +1 (sin4 + cos4 ) = (sin4 + cos4 ) = 4−1 cos4 + 2 = −4−1 sin4 + 2 · 4 + 2 = −4 sin4 + 2 = 4 sin−4 − 2 = 4 cos 2 − −4 − 2 = 4 cos4 + ( + 1) 2 which shows that +1 is true. Therefore, (sin4 + cos4 ) = 4−1 cos4 + 2 for every positive integer , by mathematical induction. Another proof: First write sin4 + cos4 = (sin2 + cos2 )2 − 2 sin2 cos2 = 1 − 1 2 sin2 2 = 1 − 1 4(1 − cos 4) = 3 4 + 1 4 cos 4 Then we have (sin4 + cos4 ) = 3 4 + 14 cos 4 = 14 · 4 cos4 + 2 = 4−1 cos4 + 2 . 10. lim → () − () √ − √ = lim → √() − − √() · √√ + + √ √ = lim → () − − () · √ + √ = lim → () − () − · lim → √ + √ = 0() · √ + √ = 2 √ 0() 11. We must find a value 0 such that the normal lines to the parabola = 2 at = ±0 intersect at a point one unit from the points ±0 2 0. The normals to = 2 at = ±0 have slopes −±210 and pass through ±0 2 0 respectively, so the normals have the equations − 2 0 = − 1 20 ( − 0) and − 2 0 = 1 20 ( + 0). The common -intercept is 2 0 + 1 2 . We want to find the value of 0 for which the distance from 0 2 0 + 1 2 to 0 2 0 equals 1. The square of the distance is (0 − 0)2 + 2 0 − 2 0 + 1 22 = 2 0 + 1 4 = 1 ⇔ 0 = ± √23. For these values of 0, the -intercept is 2 0 + 1 2 = 5 4, so the center of the circle is at 0 5 4. Another solution: Let the center of the circle be (0 ). Then the equation of the circle is 2 + ( − )2 = 1. Solving with the equation of the parabola, = 2, we get 2 + (2 − )2 = 1 ⇔ 2 + 4 − 22 + 2 = 1 ⇔ 4 + (1 − 2)2 + 2 − 1 = 0. The parabola and the circle will be tangent to each other when this quadratic equation in 2 has equal roots; that is, when the discriminant is 0. Thus, (1 − 2)2 − 4(2 − 1) = 0 ⇔ 1 − 4 + 42 − 42 + 4 = 0 ⇔ 4 = 5, so = 5 4. The center of the circle is 0 5 4. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.290 ¤ CHAPTER 3 PROBLEMS PLUS 12. See the figure. The parabolas = 42 and = + 22 intersect each other at right angles at the point ( ) if and only if ( ) satisfies both equations and the tangent lines at ( ) are perpendicular. = 42 ⇒ 0 = 8 and = + 22 ⇒ 1 = 4 0 ⇒ 0 = 1 4 , so at ( ) we must have 8 = − 1 1(4) ⇒ 8 = −4 ⇒ = −2. Since ( ) is on both parabolas, we have (1) = 42 and (2) = + 22. Substituting −2 for in (1) gives us −2 = 42 ⇒ 42 + 2 = 0 ⇒ 2(2 + 1) = 0 ⇒ = 0 or = − 1 2. If = 0, then = 0 and = 0, and the tangent lines at (0 0) are = 0 and = 0. If = − 1 2, then = −2− 1 2 = 1 and − 1 2 = + 2(1)2 ⇒ = − 5 2, and the tangent lines at − 1 2 1 are − 1 = −4 + 1 2 [or = −4 − 1] and − 1 = 1 4 + 1 2 or = 1 4 + 9 8. 13. See the figure. Clearly, the line = 2 is tangent to both circles at the point (0 2). We’ll look for a tangent line through the points ( ) and ( ), and if such a line exists, then its reflection through the -axis is another such line. The slope of is the same at ( ) and ( ). Find those slopes: 2 + 2 = 4 ⇒ 2 + 2 0 = 0 ⇒ 0 = − = − and 2 + ( − 3)2 = 1 ⇒ 2 + 2( − 3)0 = 0 ⇒ 0 = − − 3 = − − 3. Now an equation for can be written using either point-slope pair, so we get − = − ( − ) or = − + 2 + and − = − − 3( − ) or = − − 3 + −2 3 + . The slopes are equal, so − = − − 3 ⇔ − 3 = . Since ( ) is a solution of 2 + ( − 3)2 = 1 we have 2 + ( − 3)2 = 1, so 2 + 2 = 1 ⇒ 22 + 22 = 2 ⇒ 2(2 + 2) = 2 ⇒ 42 = 2 [since ( ) is a solution of 2 + 2 = 4] ⇒ = 2. Now − 3 = ⇒ = 3 + 2 , so = 3 + 2 . The -intercepts are equal, so 2 + = −2 3 + ⇔ 2 + = ( 2) 2 2 + 3 + 2 ⇔ 2 + = 22 + 3 + 2 (2) ⇔ 22 + 22 = 2 + 6 + 2 ⇔ 2 + 2 = 6 ⇔ 4 = 6 ⇔ = 2 3. It follows that = 3 + 2 = 10 3 , 2 = 4 − 2 = 4 − 4 9 = 32 9 ⇒ = 4 3√2, and 2 = 1 − ( − 3)2 = 1 − 1 32 = 8 9 ⇒ = 2 3√2. Thus, has equation − 23 = −(423) 3√2 − 43√2 ⇔ − 2 3 = −2√2 − 4 3√2 ⇔ = −2√2 + 6. Its reflection has equation = 2√2 + 6. [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 PROBLEMS PLUS ¤ 291 In summary, there are three lines tangent to both circles: = 2 touches at (0 2), touches at 4 3√2 2 3 and 2 3√2 10 3 , and its reflection through the -axis touches at − 4 3√2 2 3 and − 2 3√2 10 3 . 14. () = 46 + 45 + 2 1 + = 45( + 1) + 2 + 1 = 45( + 1) + 1 + 2 + 1 = 45 + 2( + 1)−1, so (46)() = (45)(46) + 2 ( + 1)−1(46). The forty-sixth derivative of any forty-fifth degree polynomial is 0, so (45)46 = 0. Thus, (46)() = 2 (−1)(−2)(−3) · · · (−46)( + 1)−47 = 2(46!)( + 1)−47 and (46)(3) = 2(46!)(4)−47 or (46!)2−93. 15. We can assume without loss of generality that = 0 at time = 0, so that = 12 rad. [The angular velocity of the wheel is 360 rpm = 360 · (2 rad)(60 s) = 12 rads.] Then the position of as a function of time is = (40 cos 40 sin ) = (40 cos 12 40 sin 12), so sin = 12 m = 40 sin 120 = sin 3 = 1 3 sin 12. (a) Differentiating the expression for sin , we get cos · = 1 3 · 12 · cos 12 = 4 cos . When = 3 , we have sin = 1 3 sin = √3 6 , so cos = 1 − √632 = 11 12 and = 4cos cos 3 = 11 212 = 4√11 √3 ≈ 656 rads. (b) By the Law of Cosines, | |2 = ||2 + ||2 − 2 || || cos ⇒ 1202 = 402 + ||2 − 2 · 40 | | cos ⇒ ||2 − (80 cos ) | | − 12,800 = 0 ⇒ || = 1 280 cos ± √6400 cos2 + 51,200 = 40 cos ± 40 √cos2 + 8 = 40cos + √8 + cos2 cm [since | | 0]. As a check, note that || = 160 cm when = 0 and | | = 80 √2 cm when = 2 . (c) By part (b), the -coordinate of is given by = 40cos + √8 + cos2 , so = = 40− sin − 22 cos √8 + cos sin2 · 12 = −480 sin 1 + √8 + cos cos 2 cms. In particular, = 0 cms when = 0 and = −480 cms when = 2 . 16. The equation of 1 is − 2 1 = 21( − 1) = 21 − 22 1 or = 21 − 2 1. The equation of 2 is = 22 − 2 2. Solving for the point of intersection, we get 2(1 − 2) = 2 1 − 2 2 ⇒ = 1 2(1 + 2). Therefore, the coordinates of are 1 2(1 + 2) 12. So if the point of contact of is 2, then 1 is 1 2( + 1) 1 and 2 is 1 2( + 2) 2. Therefore, | 1|2 = 1 4( − 2)2 + 2 1( − 2)2 = ( − 2)2 1 4 + 2 1 and | 1|2 = 1 4(1 − 2)2 + 2 1(1 − 2)2 = (1 − 2)2 1 4 + 2 1. So | 1|2 | 1|2 = ( − 2)2 (1 − 2)2 , and similarly || 22||22 = ((11−−2))22 . Finally, || 11|| + || 22|| = 1−−22 + 11−−2 = 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.292 ¤ CHAPTER 3 PROBLEMS PLUS 17. Consider the statement that ( sin ) = sin( + ). For = 1, ( sin ) = sin + cos , and sin( + ) = [sin cos + cos sin ] = sin + cos = sin + cos since tan = ⇒ sin = and cos = . So the statement is true for = 1. Assume it is true for = . Then +1 +1 ( sin ) = sin( + ) = sin( + ) + cos( + ) = [ sin( + ) + cos( + )] But sin[ + ( + 1)] = sin[( + ) + ] = sin( + ) cos + sin cos( + ) = sin( + ) + cos( + ). Hence, sin( + ) + cos( + ) = sin[ + ( + 1)]. So +1 +1 ( sin ) = [ sin(+)+ cos(+)] = [ sin(+(+1))] = +1[sin(+( +1))]. Therefore, the statement is true for all by mathematical induction. 18. We recognize this limit as the definition of the derivative of the function () = sin at = , since it is of the form lim → () − () − . Therefore, the limit is equal to 0() = (cos )sin = −1 · 0 = −1. 19. It seems from the figure that as approaches the point (0 2) from the right, → ∞ and → 2+. As approaches the point (3 0) from the left, it appears that → 3+ and → ∞. So we guess that ∈ (3 ∞) and ∈ (2 ∞). It is more difficult to estimate the range of values for and . We might perhaps guess that ∈ (0 3), and ∈ (−∞ 0) or (−2 0). In order to actually solve the problem, we implicitly differentiate the equation of the ellipse to find the equation of the tangent line: 2 9 + 2 4 = 1 ⇒ 29 + 24 0 = 0, so 0 = −4 9 . So at the point (0 0) on the ellipse, an equation of the tangent line is − 0 = −4 9 0 0 ( − 0) or 40 + 90 = 42 0 + 902. This can be written as 0 9 + 0 4 = 2 0 9 + 02 4 = 1, because (0 0) lies on the ellipse. So an equation of the tangent line is 0 9 + 0 4 = 1. Therefore, the -intercept for the tangent line is given by 0 9 = 1 ⇔ = 9 0 , and the -intercept is given by 0 4 = 1 ⇔ = 40 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 PROBLEMS PLUS ¤ 293 So as 0 takes on all values in (0 3), takes on all values in (3 ∞), and as 0 takes on all values in (0 2), takes on all values in (2 ∞). At the point (0 0) on the ellipse, the slope of the normal line is − 1 0(0 0) = 9 4 0 0 , and its equation is − 0 = 9 4 0 0 ( − 0). So the -intercept for the normal line is given by 0 − 0 = 9 4 0 0 ( − 0) ⇒ = − 40 9 + 0 = 50 9 , and the -intercept is given by − 0 = 9 4 0 0 (0 − 0) ⇒ = −90 4 + 0 = − 50 4 . So as 0 takes on all values in (0 3), takes on all values in 0 5 3, and as 0 takes on all values in (0 2), takes on all values in − 5 2 0. 20. lim →0 sin(3 + )2 − sin 9 = 0(3) where () = sin 2. Now 0() = (cos 2)(2), so 0(3) = 6 cos 9. 21. (a) If the two lines 1 and 2 have slopes 1 and 2 and angles of inclination 1 and 2, then 1 = tan 1 and 2 = tan 2. The triangle in the figure shows that 1 + + (180◦ − 2) = 180◦ and so = 2 − 1. Therefore, using the identity for tan( − ), we have tan = tan(2 − 1) = tan 2 − tan 1 1 + tan 2 tan 1 and so tan = 1 + 2 −112 . (b) (i) The parabolas intersect when 2 = ( − 2)2 ⇒ = 1. If = 2, then 0 = 2, so the slope of the tangent to = 2 at (1 1) is 1 = 2(1) = 2. If = ( − 2)2, then 0 = 2( − 2), so the slope of the tangent to = ( − 2)2 at (1 1) is 2 = 2(1 − 2) = −2. Therefore, tan = 2 − 1 1 + 12 = −2 − 2 1 + 2(−2) = 4 3 and so = tan−1 4 3 ≈ 53◦ [or 127◦]. (ii) 2 − 2 = 3 and 2 − 4 + 2 + 3 = 0 intersect when 2 − 4 + (2 − 3) + 3 = 0 ⇔ 2( − 2) = 0 ⇒ = 0 or 2, but 0 is extraneous. If = 2, then = ±1. If 2 − 2 = 3 then 2 − 20 = 0 ⇒ 0 = and 2 − 4 + 2 + 3 = 0 ⇒ 2 − 4 + 20 = 0 ⇒ 0 = 2 − . At (2 1) the slopes are 1 = 2 and 2 = 0, so tan = 1 + 2 0 − 2· 0 = −2 ⇒ ≈ 117◦. At (2 −1) the slopes are 1 = −2 and 2 = 0 so tan = 0 − (−2) 1 + (−2)(0) = 2 ⇒ ≈ 63◦ [or 117◦]. 22. 2 = 4 ⇒ 20 = 4 ⇒ 0 = 2 ⇒ slope of tangent at (1 1) is 1 = 21. The slope of is 2 = 1 1 − , so by the formula from Problem 19(a), tan = 1 1 − − 2 1 1 + 21 1−1 · 1 (1 − ) 1 (1 − ) = 12 − 2(1 − ) 1(1 − ) + 21 = 41 − 21 + 22 11 − 1 + 21 = 2( + 1) 1( + 1) = 2 1 = slope of tangent at = tan Since 0 ≤ , ≤ 2 , this proves that = . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.294 ¤ CHAPTER 3 PROBLEMS PLUS 23. Since ∠ = ∠ = , the triangle is isosceles, so || = || = . By the Law of Cosines, 2 = 2 + 2 − 2 cos . Hence, 2 cos = 2, so = 2 2 cos = 2 cos . Note that as → 0+, → 0+ (since sin = ), and hence → 2 cos 0 = 2 . Thus, as is taken closer and closer to the -axis, the point approaches the midpoint of the radius . 24. lim →0 () () = lim →0 (()) −− 00 = lim →0 ( ( ) ) − − (0) (0) = lim →0 () − (0) − 0 () − (0) − 0 = lim →0 () − (0) − 0 lim →0 () − (0) − 0 = 0(0) 0(0) 25. lim →0 sin( + 2) − 2 sin( + ) + sin 2 = lim →0 sin cos 2 + cos sin 2 − 2 sin cos − 2 cos sin + sin 2 = lim →0 sin (cos 2 − 2 cos + 1) + cos (sin 2 − 2 sin ) 2 = lim →0 sin (2 cos2 − 1 − 2 cos + 1) + cos (2 sin cos − 2 sin ) 2 = lim →0 sin (2 cos )(cos − 1) + cos (2 sin)(cos − 1) 2 = lim →0 2(cos − 1)[sin cos + cos sin ](cos + 1) 2(cos + 1) = lim →0 −2 sin2 [sin( + )] 2(cos + 1) = −2 lim →0 sin2 · sin( cos++ 1 ) = −2(1)2 sin( cos 0 + 1 + 0) = − sin 26. (a) () = ( − 2)( − 6) = 3 − 82 + 12 ⇒ 0() = 32 − 16 + 12. The average of the first pair of zeros is (0 + 2)2 = 1. At = 1, the slope of the tangent line is 0(1) = −1, so an equation of the tangent line has the form = −1 + . Since (1) = 5, we have 5 = −1 + ⇒ = 6 and the tangent has equation = − + 6. Similarly, at = 0 + 6 2 = 3, = −9 + 18; at = 2 + 6 2 = 4, = −4. From the graph, we see that each tangent line drawn at the average of two zeros intersects the graph of at the third zero. (b) A CAS gives 0() = ( − )( − ) + ( − )( − ) + ( − )( − ) or 0() = 32 − 2( + + ) + + + . Using the Simplify command, we get 0 +2 = −( −4 )2 and +2 = −( −8 )2 ( + − 2), so an equation of the tangent line at = +2 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 PROBLEMS PLUS ¤ 295 is = −( − )2 4 − +2 − ( −8 )2 ( + − 2). To find the -intercept, let = 0 and use the Solve command. The result is = Using Derive, we can begin by authoring the expression ( − )( − )( − ). Now load the utility file DifferentiationApplications. Next we author tangent (#1 ( + )2)—this is the command to find an equation of the tangent line of the function in #1 whose independent variable is at the -value ( + )2. We then simplify that expression and obtain the equation = #4. The form in expression #4 makes it easy to see that the -intercept is the third zero, namely . In a similar fashion we see that is the -intercept for the tangent line at ( + )2 and is the -intercept for the tangent line at ( + )2. 27. Let () = 2 and () = √ [ 0]. From the graphs of and , we see that will intersect exactly once when and share a tangent line. Thus, we must have = and 0 = 0 at = . () = () ⇒ 2 = √ () and 0() = 0() ⇒ 22 = 2 √ ⇒ 2 = 4 √ . So we must have √ = 4 √ ⇒ √ 2 = 4 ⇒ = 1 4. From (), 2(14) = 14 ⇒ = 212 = 2 √ ≈ 3297. 28. We see that at = 0, () = = 1 + = 1, so if = is to lie above = 1 + , the two curves must just touch at (0 1), that is, we must have 0(0) = 1. [To see this analytically, note that ≥ 1 + ⇒ − 1 ≥ ⇒ − 1 ≥ 1 for 0, so 0(0) = lim →0+ − 1 ≥ 1. Similarly, for 0, − 1 ≥ ⇒ − 1 ≤ 1, so 0(0) = lim →0− − 1 ≤ 1. [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.296 ¤ CHAPTER 3 PROBLEMS PLUS Since 1 ≤ 0(0) ≤ 1, we must have 0(0) = 1.] But 0() = ln ⇒ 0(0) = ln , so we have ln = 1 ⇔ = . Another method: The inequality certainly holds for ≤ −1, so consider −1, 6= 0. Then ≥ 1 + ⇒ ≥ (1 + )1 for 0 ⇒ ≥ lim →0+ (1 + )1 = , by Equation 3.6.5. Also, ≥ 1 + ⇒ ≤ (1 + )1 for 0 ⇒ ≤ lim →0− (1 + )1 = . So since ≤ ≤ , we must have = . 29. = √2− 1 − √22− 1 arctan + √2sin −1 + cos . Let = + √2 − 1. Then 0 = √21− 1 − √22− 1 · 1 + sin2 1( + cos )2 · cos ((+ cos + cos) + sin )2 2 = 1 √2 − 1 − 2 √2 − 1 · cos + cos2 + sin2 ( + cos )2 + sin2 = 1 √2 − 1 − 2 √2 − 1 · cos + 1 2 + 2 cos + 1 = 2 + 2 cos + 1 − 2 cos − 2 √2 − 1 (2 + 2 cos + 1) = 2 − 1 √2 − 1 (2 + 2 cos + 1) But 2 = 22 + 2 √2 − 1 − 1 = 2 + √2 − 1 − 1 = 2 − 1, so 2 + 1 = 2, and 2 − 1 = 2( − 1). So 0 = √2 − 1 (2 2( −+ 2 1) cos ) = √2 − 1 (− 1+ cos ). But − 1 = 2 + √2 − 1 − 1 = √2 − 1, so 0 = 1( + cos ). 30. Suppose that = + is a tangent line to the ellipse. Then it intersects the ellipse at only one point, so the discriminant of the equation 2 2 + ( + )2 2 = 1 ⇔ (2 + 22)2 + 22 + 22 − 22 = 0 must be 0; that is, 0 = (22)2 − 4(2 + 22)(22 − 22) = 4422 − 4222 + 424 − 4422 + 4422 = 422(22 + 2 − 2) Therefore, 22 + 2 − 2 = 0. Now if a point ( ) lies on the line = + , then = − , so from above, 0 = 22 + 2 − ( − )2 = (2 − 2)2 + 2 + 2 − 2 ⇔ 2 + 2 2 − 2 + 2 − 2 2 − 2 = 0. (a) Suppose that the two tangent lines from the point ( ) to the ellipse have slopes and 1 . Then and 1 are roots of the equation 2 + 2 2 − 2 + 2 − 2 2 − 2 = 0. This implies that ( − ) − 1 = 0 ⇔ 2 − + 1 + 1 = 0, so equating the constant terms in the two quadratic equations, we get 2 − 2 2 − 2 = 1 = 1, and hence 2 − 2 = 2 − 2. So ( ) lies on the hyperbola 2 − 2 = 2 − 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 PROBLEMS PLUS ¤ 297 (b) If the two tangent lines from the point ( ) to the ellipse have slopes and − 1 , then and − 1 are roots of the quadratic equation, and so ( − ) + 1 = 0, and equating the constant terms as in part (a), we get 2 − 2 2 − 2 = −1, and hence 2 − 2 = 2 − 2. So the point ( ) lies on the circle 2 + 2 = 2 + 2. 31. = 4 − 22 − ⇒ 0 = 43 − 4 − 1. The equation of the tangent line at = is − (4 − 22 − ) = (43 − 4 − 1)( − ) or = (43 − 4 − 1) + (−34 + 22) and similarly for = . So if at = and = we have the same tangent line, then 43 − 4 − 1 = 43 − 4 − 1 and −34 + 22 = −34 + 22. The first equation gives 3 − 3 = − ⇒ ( − )(2 + + 2) = ( − ). Assuming 6= , we have 1 = 2 + + 2. The second equation gives 3(4 − 4) = 2(2 − 2) ⇒ 3(2 − 2)(2 + 2) = 2(2 − 2) which is true if = −. Substituting into 1 = 2 + + 2 gives 1 = 2 − 2 + 2 ⇒ = ±1 so that = 1 and = −1 or vice versa. Thus, the points (1 −2) and (−1 0) have a common tangent line. As long as there are only two such points, we are done. So we show that these are in fact the only two such points. Suppose that 2 − 2 6= 0. Then 3(2 − 2)(2 + 2) = 2(2 − 2) gives 3(2 + 2) = 2 or 2 + 2 = 2 3. Thus, = (2 + + 2) − (2 + 2) = 1 − 2 3 = 1 3 , so = 1 3 . Hence, 2 + 1 92 = 2 3 , so 94 + 1 = 62 ⇒ 0 = 94 − 62 + 1 = (32 − 1)2. So 32 − 1 = 0 ⇒ 2 = 1 3 ⇒ 2 = 1 92 = 1 3 = 2, contradicting our assumption that 2 6= 2. 32. Suppose that the normal lines at the three points 1 2 1, 2 2 2, and 3 2 3 intersect at a common point. Now if one of the is 0 (suppose 1 = 0) then by symmetry 2 = −3, so 1 + 2 + 3 = 0. So we can assume that none of the is 0. The slope of the tangent line at 2 is 2, so the slope of the normal line is −21 and its equation is − 2 = − 1 2 ( − ). We solve for the -coordinate of the intersection of the normal lines from 1 2 1 and 2 2 2: = 2 1 − 1 21 ( − 1) = 2 2 − 1 22 ( − 2) ⇒ 212 − 211 = 2 2 − 2 1 ⇒ 21−122 = (−1 − 2)(1 + 2) ⇔ = −212(1 + 2) (1). Similarly, solving for the -coordinate of the intersections of the normal lines from 1 2 1 and 3 2 3 gives = −213(1 + 3) (2). Equating (1) and (2) gives 2(1 + 2) = 3(1 + 3) ⇔ 1(2 − 3) = 2 3 − 2 2 = −(2 + 3)(2 − 3) ⇔ 1 = −(2 + 3) ⇔ 1 + 2 + 3 = 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.298 ¤ CHAPTER 3 PROBLEMS PLUS 33. Because of the periodic nature of the lattice points, it suffices to consider the points in the 5 × 2 grid shown. We can see that the minimum value of occurs when there is a line with slope 2 5 which touches the circle centered at (3 1) and the circles centered at (0 0) and (5 2). To find , the point at which the line is tangent to the circle at (0 0), we simultaneously solve 2 + 2 = 2 and = − 5 2 ⇒ 2 + 25 4 2 = 2 ⇒ 2 = 29 4 2 ⇒ = √229 , = − √529 . To find , we either use symmetry or solve ( − 3)2 + ( − 1)2 = 2 and − 1 = − 5 2( − 3). As above, we get = 3 − √229 , = 1 + √529 . Now the slope of the line is 2 5, so = 1 + √529 − − √529 3 − √229 − √229 = 1 + √10 29 3 − √429 = √29 + 10 3 √29 − 4 = 2 5 ⇒ 5 √29 + 50 = 6 √29 − 8 ⇔ 58 = √29 ⇔ = √58 29. So the minimum value of for which any line with slope 2 5 intersects circles with radius centered at the lattice points on the plane is = √58 29 ≈ 0093. 34. Assume the axes of the cone and the cylinder are parallel. Let denote the initial height of the water. When the cone has been dropping for seconds, the water level has risen centimeters, so the tip of the cone is + 1 centimeters below the water line. We want to find when + = (when the cone is completely submerged). Using similar triangles, 1 + = ⇒ 1 = ( + ). volume of water and cone at time = original volume of water + volume of submerged part of cone 2( + ) = 2 + 1 312( + ) 2 + 2 = 2 + 1 3 2 2 ( + )3 322 = 2( + )3 Differentiating implicitly with respect to gives us 322 = 23( + )2 + 3( + )2 ⇒ = 2( + )2 22 − 2( + )2 ⇒ + = = 22 22 − 22 = 2 2 − 2 . Thus, the water level is rising at a rate of 2 2 − 2 cms at the instant the cone is completely submerged. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 3 PROBLEMS PLUS ¤ 299 35. By similar triangles, 5 = 16 ⇒ = 5 16 . The volume of the cone is = 1 32 = 1 3516 2 = 25 768 3, so = 25 256 2 . Now the rate of change of the volume is also equal to the difference of what is being added (2 cm3min) and what is oozing out (, where is the area of the cone and is a proportionality constant). Thus, = 2 − . Equating the two expressions for and substituting = 10, = −03, = 5(10) 16 = 25 8 , and √281 = 10 16 ⇔ = 5 8 √281, we get 25 256 (10)2(−03) = 2 − 25 8 · 5 8 √281 ⇔ 125 √281 64 = 2 + 750 256 . Solving for gives us = 256 + 375 250 √281 . To maintain a certain height, the rate of oozing, , must equal the rate of the liquid being poured in; that is, = 0. Thus, the rate at which we should pour the liquid into the container is = 256 + 375 250 √281 · · 25 8 · 5 √281 8 = 256 + 375 128 ≈ 11204 cm3min °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.300 ¤ CHAPTER 3 PROBLEMS PLUS °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved. [Show More]
Last updated: 3 years ago
Preview 1 out of 1 pages

Buy this document to get the full access instantly
Instant Download Access after purchase
Buy NowInstant download
We Accept:

Reviews( 0 )
$11.00
Can't find what you want? Try our AI powered Search
Document information
Connected school, study & course
About the document
Uploaded On
Jan 06, 2020
Number of pages
1
Written in
All
Additional information
This document has been written for:
Uploaded
Jan 06, 2020
Downloads
0
Views
83


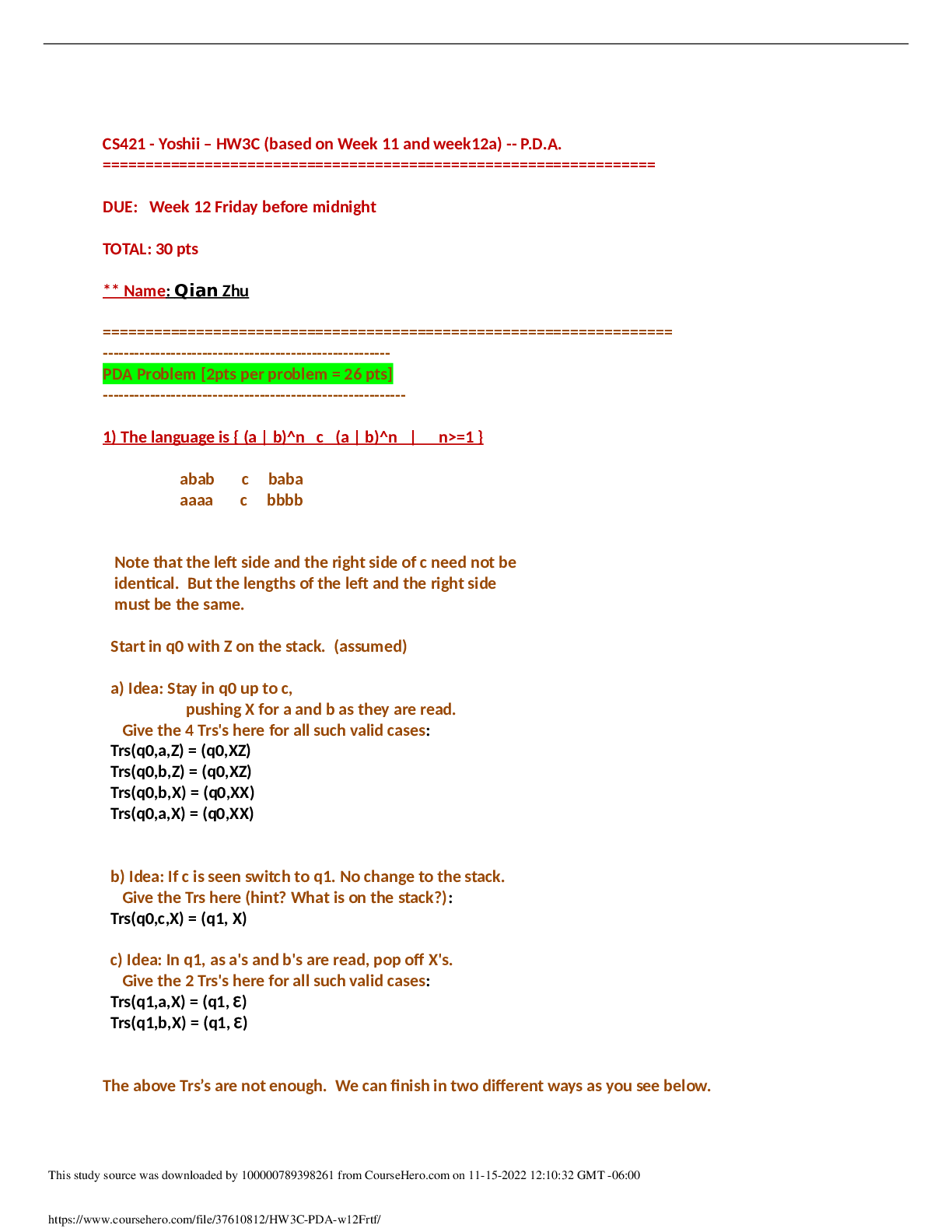


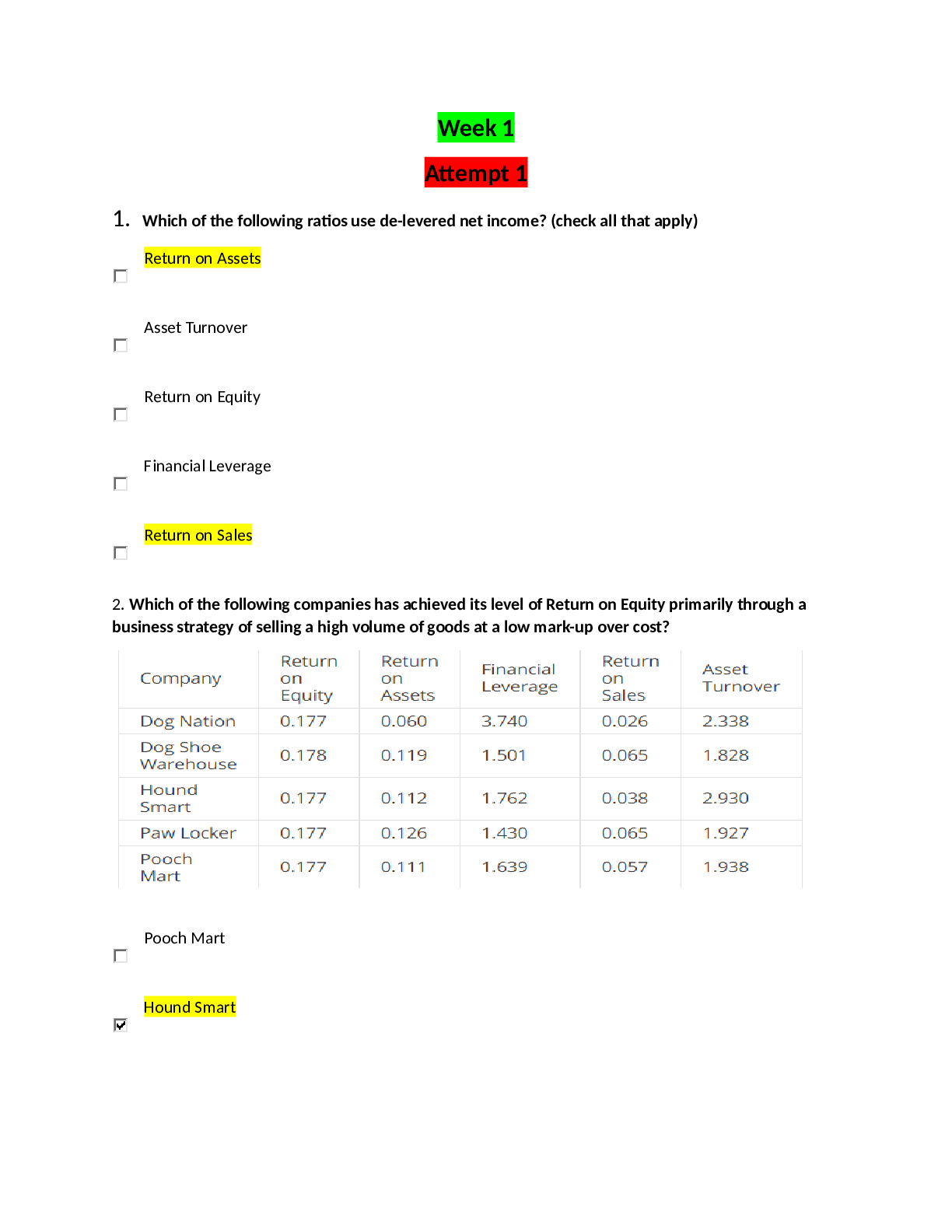
.png)
.png)
.png)
.png)
.png)
.png)
.png)