Calculus > QUESTIONS & ANSWERS > Chapter 11: INFINITE SEQUENCES AND SERIES. Work and Answers (All)
Chapter 11: INFINITE SEQUENCES AND SERIES. Work and Answers
Document Content and Description Below
11.1 Sequences 1. (a) A sequence is an ordered list of numbers. It can also be defined as a function whose domain is the set of positive integers. (b) The terms approach 8 as becomes larg ... e. In fact, we can make as close to 8 as we like by taking sufficiently large. (c) The terms become large as becomes large. In fact, we can make as large as we like by taking sufficiently large. 2. (a) From Definition 1, a convergent sequence is a sequence for which lim →∞ exists. Examples: {1}, {12} (b) A divergent sequence is a sequence for which lim →∞ does not exist. Examples: {}, {sin} 3. = 2 2 + 1 , so the sequence is 2(1) + 1 21 2(2) + 1 22 2(3) + 1 23 2(4) + 1 24 2(5) + 1 25 = 23 45 87 16 9 32 11 . 4. = 2 − 1 2 + 1, so the sequence is 1 1 + 1 − 1 4 4 + 1 − 1 9 9 + 1 − 1 16 16 + 1 − 1 25 25 + 1 − 1 = 0 35 10 8 15 17 24 26 . 5. = (−1)−1 5 , so the sequence is 511 −521 513 −541 515 = 15 −25 1 125 1 −625 1 3125 1 . 6. = cos 2 , so the sequence is cos 2 coscos 32 cos 2 cos 52 = {0 −1 0 10 }. 7. = 1 ( + 1)!, so the sequence is 2! 1 3! 1 4! 1 5! 1 6! 1 = 12 16 24 1 120 1 720 1 . 8. = (−1) ! + 1 , so 1 = (−1)11 1! + 1 = −1 2 , and the sequence is −21 2 + 1 2 6 + 1 −3 24 + 1 4 120 + 1 −5 = −1 2 23 −37 25 4 −121 5 . 9. 1 = 1, +1 = 5 − 3. Each term is defined in terms of the preceding term. 2 = 51 − 3 = 5(1) − 3 = 2. 3 = 52 − 3 = 5(2) − 3 = 7. 4 = 53 − 3 = 5(7) − 3 = 32. 5 = 54 − 3 = 5(32) − 3 = 157. The sequence is {1 2732 157 }. 10. 1 = 6, +1 = . 2 = 1 1 = 6 1 = 6. 3 = 2 2 = 6 2 = 3. 4 = 3 3 = 3 3 = 1. 5 = 4 4 = 1 4 . The sequence is 6 6 3 1 1 4 . 11. 1 = 2, +1 = 1 + . 2 = 1 1 + 1 = 2 1 + 2 = 2 3 . 3 = 2 1 + 2 = 23 1 + 23 = 2 5 . 4 = 3 1 + 3 = 25 1 + 25 = 2 7 . 5 = 4 1 + 4 = 27 1 + 27 = 2 9 . The sequence is 2 2 3 2 5 2 7 2 9 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. 957 FOR INSTRUCTOR USE ONLYNOT FOR SALE 958 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 12. 1 = 2, 2 = 1, +1 = − −1. Each term is defined in term of the two preceding terms. 3 = 2 − 1 = 1 − 2 = −1. 4 = 3 − 2 = −1 − 1 = −2. 5 = 4 − 3 = −2 − (−1) = −1. 6 = 5 − 4 = −1 − (−2) = 1. The sequence is {2 1 −1 −2 −11 }. 13. 1 2 , 1 4 , 1 6 , 1 8 , 10 1 , . The denominator is two times the number of the term, , so = 21. 14. 4, −1, 1 4 , − 16 1 , 64 1 , . The first term is 4 and each term is − 1 4 times the preceding one, so = 4− 1 4−1. 15. −32 − 4 3 8 9 − 16 27 . The first term is −3 and each term is − 2 3 times the preceding one, so = −3− 2 3−1. 16. {581114 17 }. Each term is larger than the preceding term by 3, so = 1 + ( − 1) = 5 + 3( − 1) = 3 + 2. 17. 1 2 − 4 3 9 4 − 16 5 25 6 . The numerator of the nth term is 2 and its denominator is + 1. Including the alternating signs, we get = (−1)+1 2 + 1 . 18. {10 −10 1 0 −10 }. Two possibilities are = sin 2 and = cos ( − 1) 2 . 19. = 3 1 + 6 1 04286 2 04615 3 04737 4 04800 5 04839 6 04865 7 04884 8 04898 9 04909 10 04918 It appears that lim →∞ = 05. lim →∞ 3 1 + 6 = lim →∞ (3) (1 + 6) = lim →∞ 13+ 6 = 36 = 1 2 20. = 2 + (−1) 1 10000 2 25000 3 16667 4 22500 5 18000 6 21667 7 18571 8 21250 9 18889 10 21000 It appears that lim →∞ = 2. lim →∞ 2 + (−1) = lim →∞2 + lim →∞ (−1) = 2 + 0 = 2 since lim →∞ 1 = 0 and by Theorem 6, lim →∞ (−1) = 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.1 SEQUENCES ¤ 959 21. = 1 + − 1 2 1 05000 2 12500 3 08750 4 10625 5 09688 6 10156 7 09922 8 10039 9 09980 10 10010 It appears that lim →∞ = 1. lim →∞ 1 + − 1 2 = lim →∞ 1 + lim →∞ − 1 2 = 1 + 0 = 1 since lim →∞ − 1 2 = 0 by (9). 22. = 1 + 10 9 1 21111 2 22346 3 23717 4 25242 5 26935 6 28817 7 30908 8 33231 9 35812 10 38680 It appears that the sequence does not have a limit. lim →∞ 10 9 = lim →∞10 9 , which diverges by (9) since 10 9 1. 23. = 3 + 52 + 2 = (3 + 52)2 ( + 2)2 = 5 + 32 1 + 1 , so → 5 + 0 1 + 0 = 5 as → ∞. Converges 24. = 3 + 52 1 + = (3 + 52) (1 + ) = 3 + 5 1 + 1 , so → ∞ as → ∞ since lim →∞3 + 5 = ∞ and lim →∞1 + 1 = 0 + 1 = 1. Diverges 25. = 4 3 − 2 = 43 (3 − 2)3 = 1 − 2 / 2 , so → ∞ as → ∞ since lim →∞ = ∞ and lim →∞1 − 22 = 1 − 0 = 1. Diverges 26. = 2 + (086) → 2 + 0 = 2 as → ∞ since lim →∞ (086) = 0 by (9) with = 086. Converges 27. = 37− = 3 7 = 73, so lim →∞ = 0 by (9) with = 37. Converges °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 960 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 28. = √3√+ 2 = (√3√+ 2) √√ = 1 + 23√ → 1 + 0 3 = 3 as → ∞. Converges 29. Because the natural exponential function is continuous at 0, Theorem 7 enables us to write lim →∞ = lim →∞ −1√ = lim →∞(−1√) = 0 = 1. Converges 30. = 4 1 + 9 = 49 (1 + 9)9 = (49) (19) + 1 → 0 0 + 1 = 0 as → ∞ since lim →∞4 9 = 0 and lim →∞1 9 = 0 by (9). Converges 31. = 1 + 4 1 + 22 = (1 + 4 (1 + 22)) 22 = (1 (1 2 2) + 4 ) + 1 → √4 = 2 as → ∞ since lim →∞(12) = 0. Converges 32. = cos + 1 = cos( + 1) = cos 1 + 1 , so → cos = −1 as → ∞ since lim →∞1 = 0 Converges 33. = √3+ 4 2 = √3+ 4 2√ 3√3 = 1 + 4 √2 , so → ∞ as → ∞ since lim →∞√ = ∞ and lim →∞ 1 + 42 = 1. Diverges 34. If = 2 + 2 , then lim →∞ = lim →∞ (2) ( + 2) = lim →∞ 1 + 2 2 = 21 = 2. Since the natural exponential function is continuous at 2, by Theorem 7, lim →∞ 2(+2) = lim→∞ = 2. Converges 35. lim →∞ || = lim →∞ (−1) 2√ = 1 2 lim →∞ 1 12 = 1 2 (0) = 0, so lim →∞ = 0 by (6). Converges 36. lim →∞ + √ = lim →∞ ( + √) = lim →∞ 1 + 11√ = 1 + 0 1 = 1. Thus, = (−1) +√+1 has odd-numbered terms that approach 1 and even-numbered terms that approach −1 as → ∞, and hence, the sequence {} is divergent. 37. = (2 − 1)! (2 + 1)! = (2 − 1)! (2 + 1)(2)(2 − 1)! = 1 (2 + 1)(2) → 0 as → ∞. Converges 38. = ln ln 2 = ln ln 2 + ln = 1 ln 2 ln + 1 → 1 0 + 1 = 1 as → ∞. Converges 39. = sin. This sequence diverges since the terms don’t approach any particular real number as → ∞. The terms take on values between −1 and 1. Diverges 40. = tan−1 . lim →∞ tan−1 = lim →∞ tan−1 = 2 by (3), so lim →∞ = 0. Converges 41. = 2− = 2 . Since lim →∞ 2 H = lim →∞ 2 H = lim →∞ 2 = 0, it follows from Theorem 3 that lim →∞ = 0. Converges °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.1 SEQUENCES ¤ 961 42. = ln( + 1) − ln = ln + 1 = ln1 + 1 → ln (1) = 0 as → ∞ because ln is continuous. Converges 43. 0 ≤ cos2 2 ≤ 1 2 [since 0 ≤ cos2 ≤ 1], so since lim →∞ 1 2 = 0, cos 22 converges to 0 by the Squeeze Theorem. 44. = √ 21+3 = (21+3)1 = (2123)1 = 2123 = 8 · 21, so lim →∞ = 8 lim →∞ 21 = 8 · 2lim→∞(1) = 8 · 20 = 8 by Theorem 7, since the function () = 2 is continuous at 0. Converges 45. = sin(1) = sin(1) 1 . Since lim →∞ sin(1 1) = lim →0+ sin [where = 1] = 1, it follows from Theorem 3 that {} converges to 1. 46. = 2− cos. 0 ≤ cos 2 ≤ 1 2 = 21, so lim →∞|| = 0 by (9), and lim →∞ = 0 by (6) Converges 47. = 1 + 2 ⇒ ln = ln1 + 2, so lim →∞ ln = lim →∞ ln(1 + 2) 1 H = lim →∞ 1 + 2 1 −22 −12 = lim →∞ 1 + 2 2 = 2 ⇒ lim →∞1 + 2 = lim →∞ln = 2, so by Theorem 3, lim →∞1 + 2 = 2. Converges 48. = 1 ⇒ ln = 1 ln, so lim →∞ ln = lim →∞ ln H = lim →∞ 1 1 = lim →∞ 1 = 0 ⇒ lim →∞ 1 = lim →∞ ln = 0 = 1, so by Theorem 3, lim →∞ √ = 1. Converges 49. = ln(22 + 1) − ln(2 + 1) = ln222+ 1 + 1 = ln2 + 1 1 + 1 2 2 → ln 2 as → ∞. Converges 50. lim →∞ (ln)2 H = lim →∞ 2(ln)(1) 1 = 2 lim →∞ ln H = 2 lim →∞ 1 1 = 0, so by Theorem 3, lim →∞ (ln)2 = 0. Converges 51. = arctan(ln). Let () = arctan(ln). Then lim →∞ () = 2 since ln → ∞ as → ∞ and arctan is continuous. Thus, lim →∞ = lim →∞ () = 2 . Converges 52. = − √ + 1√ + 3 = − √2 + 4 + 3 = − √2 + 4 + 3 1 · + √2 + 4 + 3 + √2 + 4 + 3 = 2 − (2 + 4 + 3) + √2 + 4 + 3 = −4 − 3 + √2 + 4 + 3 = (−4 − 3) + √2 + 4 + 3 = −4 − 3 1 + 1 + 4 + 32 , so lim →∞ = −4 − 0 1 + √1 + 0 + 0 = −4 2 = −2. Converges °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 962 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 53. {010010001 } diverges since the sequence takes on only two values, 0 and 1, and never stays arbitrarily close to either one (or any other value) for sufficiently large. 54. 1 1 1 3 1 2 1 4 1 3 1 5 1 4 1 6 . 2−1 = 1 and 2 = 1 + 2 for all positive integers . lim →∞ = 0 since lim →∞ 2−1 = lim →∞ 1 = 0 and lim →∞ 2 = lim →∞ 1 + 2 = 0. For sufficiently large, can be made as close to 0 as we like. Converges 55. = ! 2 = 1 2 · 2 2 · 3 2 · · · · · ( − 1) 2 · 2 ≥ 1 2 · 2 [for 1] = 4 → ∞ as → ∞, so {} diverges. 56. 0 || = 3 ! = 3 1 · 3 2 · 3 3 · · · · · 3 ( − 1) · 3 ≤ 3 1 · 3 2 · 3 [for 2] = 27 2 → 0 as → ∞, so by the Squeeze Theorem and Theorem 6, {(−3)!} converges to 0. 57. From the graph, it appears that the sequence {} = (−1) + 1 is divergent, since it oscillates between 1 and −1 (approximately). To prove this, suppose that {} converges to . If = + 1 , then {} converges to 1, and lim →∞ = 1 = . But = (−1), so lim →∞ does not exist. This contradiction shows that {} diverges. 58. From the graph, it appears that the sequence converges to 0. || = sin = |sin| || ≤ 1 , so lim →∞ || = 0. By (6), it follows that lim →∞ = 0. 59. From the graph, it appears that the sequence converges to a number between 07 and 08. = arctan2+ 4 2 = arctan(2+ 4) 222 = arctan1 + 4 12 → arctan 1 = 4 [≈ 0785] as → ∞. 60. From the graph, it appears that the sequence converges to 5 5 = √ 5 ≤ √ 3 + 5 ≤ √ 5 + 5 = √ 2 √ 5 = √ 2 · 5 → 5 as → ∞ lim →∞21 = 20 = 1 Hence, → 5by the Squeeze Theorem. [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.1 SEQUENCES ¤ 963 Alternate solution: Let = (3 + 5)1. Then lim →∞ ln = lim →∞ ln (3 + 5) H = lim →∞ 3 ln 3 + 5 ln 5 3 + 5 = lim →∞ 3 5 ln 3 + ln 5 3 5 + 1 = ln 5, so lim →∞ = ln 5 = 5, and so √ 3 + 5 converges to 5. 61. From the graph, it appears that the sequence {} = 1 + 2 cos 2 is divergent, since it oscillates between 1 and −1 (approximately). To prove this, suppose that {} converges to . If = 2 1 + 2 , then {} converges to 1, and lim →∞ = 1 = . But = cos, so lim →∞ does not exist. This contradiction shows that {} diverges. 62. From the graphs, it seems that the sequence diverges. = 1 · 3 · 5 · · · · · (2 − 1) ! . We first prove by induction that ≥ 23−1 for all . This is clearly true for = 1, so let () be the statement that the above is true for . We must show it is then true for + 1. +1 = · 2 + 1 + 1 ≥ 23−1 · 2+ 1 + 1 (induction hypothesis). But 2+ 1 + 1 ≥ 32 [since 2(2 + 1) ≥ 3( + 1) ⇔ 4 + 2 ≥ 3 + 3 ⇔ ≥ 1], and so we get that +1 ≥ 3 2 −1 · 3 2 = 3 2 which is ( + 1). Thus, we have proved our first assertion, so since 3 2 −1 diverges [by (9)], so does the given sequence {}. 63. From the graph, it appears that the sequence approaches 0. 0 = 1 · 3 · 5 · · · · · (2 − 1) (2) = 1 2 · 3 2 · 5 2 · · · · · 2 − 1 2 ≤ 1 2 · (1) · (1) · · · · · (1) = 1 2 → 0 as → ∞ So by the Squeeze Theorem, 1 · 3 · 5 · · · · · (2)(2 − 1) converges to 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 964 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 64. (a) 1 = 1, +1 = 4 − for ≥ 1. 1 = 1, 2 = 4 − 1 = 4 − 1 = 3, 3 = 4 − 2 = 4 − 3 = 1, 4 = 4 − 3 = 4 − 1 = 3, 5 = 4 − 4 = 4 − 3 = 1. Since the terms of the sequence alternate between 1 and 3, the sequence is divergent. (b) 1 = 2, 2 = 4 − 1 = 4 − 2 = 2, 3 = 4 − 2 = 4 − 2 = 2. Since all of the terms are 2, lim →∞ = 2 and hence, the sequence is convergent. 65. (a) = 1000(106) ⇒ 1 = 1060, 2 = 112360, 3 = 119102, 4 = 126248, and 5 = 133823. (b) lim →∞ = 1000 lim →∞ (106), so the sequence diverges by (9) with = 106 1. 66. (a) Substitute 1 to 6 for in = 10010025 00025 − 1 − to get 1 = $0, 2 = $025, 3 = $075, 4 = $150, 5 = $251, and 6 = $376. (b) For two years, use 2 · 12 = 24 for to get $7028. 67. (a) We are given that the initial population is 5000, so 0 = 5000. The number of catfish increases by 8% per month and is decreased by 300 per month, so 1 = 0 + 8%0 − 300 = 1080 − 300, 2 = 1081 − 300, and so on. Thus, = 108−1 − 300. (b) Using the recursive formula with 0 = 5000, we get 1 = 5100, 2 = 5208, 3 = 5325 (rounding any portion of a catfish), 4 = 5451, 5 = 5587, and 6 = 5734, which is the number of catfish in the pond after six months. 68. +1 = 31 2+ 1 if if is an even number is an odd number When 1 = 11, the first 40 terms are 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4. When 1 = 25, the first 40 terms are 25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4. The famous Collatz conjecture is that this sequence always reaches 1, regardless of the starting point 1. 69. If || ≥ 1, then {} diverges by (9), so {} diverges also, since || = || ≥ ||. If || 1 then lim →∞ = lim →∞ − H = lim →∞ 1 (−ln)− = lim →∞ −ln = 0, so lim →∞ = 0, and hence {} converges whenever || 1. 70. (a) Let lim →∞ = . By Definition 2, this means that for every 0 there is an integer such that | − | whenever . Thus, |+1 − | whenever + 1 ⇔ − 1. It follows that lim →∞ +1 = and so lim →∞ = lim →∞ +1. (b) If = lim →∞ then lim →∞ +1 = also, so must satisfy = 1(1 + ) ⇒ 2 + − 1 = 0 ⇒ = −1 +2 √5 (since has to be nonnegative if it exists). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.1 SEQUENCES ¤ 965 71. Since {} is a decreasing sequence, +1 for all ≥ 1. Because all of its terms lie between 5 and 8, {} is a bounded sequence. By the Monotonic Sequence Theorem, {} is convergent; that is, {} has a limit . must be less than 8 since {} is decreasing, so 5 ≤ 8. 72. Since {} = {cos} ≈ {054 −042 −099 −065 028 }, the sequence is not monotonic. The sequence is bounded since −1 ≤ cos ≤ 1 for all . 73. = 1 2 + 3 is decreasing since +1 = 1 2( + 1) + 3 = 1 2 + 5 1 2 + 3 = for each ≥ 1. The sequence is bounded since 0 ≤ 1 5 for all ≥ 1. Note that 1 = 1 5. 74. +1 ⇔ 1 − 2 + 1 − ( + 1) 2 + ( + 1) ⇔ 1 − 2 + − + 3 ⇔ −2 − 2 + 3 −2 − 2 ⇔ 3 0, which is true for all ≥ 1, so {} is decreasing. Since 1 = 0 and lim →∞ 1 − 2 + = lim →∞ 1 − 1 2 + 1 = −1, the sequence is bounded (−1 ≤ 0). 75. The terms of = (−1) alternate in sign, so the sequence is not monotonic. The first five terms are −1, 2, −3, 4, and −5. Since lim →∞ || = lim →∞ = ∞, the sequence is not bounded. 76. Since {} = 2 + (−1) = 12 1 21 2 3 , the sequence is not monotonic. The sequence is bounded since 1 ≤ ≤ 5 2 for all . 77. = 3 − 2−. Let () = 3 − 2−. Then 0() = 0 − 2[(−−) + −] = 2−( − 1), which is positive for 1, so is increasing on (1 ∞). It follows that the sequence {} = {()} is increasing. The sequence is bounded below by 1 = 3 − 2−1 ≈ 226 and above by 3, so the sequence is bounded. 78. = 3 − 3 + 3. Let () = 3 − 3 + 3. Then 0() = 32 − 3 = 3(2 − 1), which is positive for 1, so is increasing on (1 ∞). It follows that the sequence {} = {()} is increasing. The sequence is bounded below by 1 = 1, but is not bounded above, so it is not bounded. 79. For √2, 2√2, 22√2, , 1 = 212, 2 = 234, 3 = 278, , so = 2(2−1)2 = 21−(12). lim →∞ = lim →∞ 21−(12) = 21 = 2. Alternate solution: Let = lim →∞ . (We could show the limit exists by showing that {} is bounded and increasing.) Then must satisfy = √2 · ⇒ 2 = 2 ⇒ ( − 2) = 0. 6= 0 since the sequence increases, so = 2. 80. (a) Let be the statement that +1 ≥ and ≤ 3. 1 is obviously true. We will assume that is true and then show that as a consequence +1 must also be true. +2 ≥ +1 ⇔ √2 + +1 ≥ √2 + ⇔ 2 + +1 ≥ 2 + ⇔ +1 ≥ , which is the induction hypothesis. +1 ≤ 3 ⇔ √2 + ≤ 3 ⇔ °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 966 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 2 + ≤ 9 ⇔ ≤ 7, which is certainly true because we are assuming that ≤ 3. So is true for all , and so 1 ≤ ≤ 3 (showing that the sequence is bounded), and hence by the Monotonic Sequence Theorem, lim →∞ exists. (b) If = lim →∞ , then lim →∞ +1 = also, so = √2 + ⇒ 2 = 2 + ⇔ 2 − − 2 = 0 ⇔ ( + 1)( − 2) = 0 ⇔ = 2 [since can’t be negative]. 81. 1 = 1, +1 = 3 − 1 . We show by induction that {} is increasing and bounded above by 3. Let be the proposition that +1 and 0 3. Clearly 1 is true. Assume that is true. Then +1 ⇒ 1 +1 1 ⇒ − 1 +1 − 1 . Now +2 = 3 − 1 +1 3 − 1 = +1 ⇔ +1. This proves that {} is increasing and bounded above by 3, so 1 = 1 3, that is, {} is bounded, and hence convergent by the Monotonic Sequence Theorem. If = lim →∞ , then lim →∞ +1 = also, so must satisfy = 3 − 1 ⇒ 2 − 3 + 1 = 0 ⇒ = 3 ±2√5 . But 1, so = 3 +2√5 . 82. 1 = 2, +1 = 1 3 − . We use induction. Let be the statement that 0 +1 ≤ ≤ 2. Clearly 1 is true, since 2 = 1(3 − 2) = 1. Now assume that is true. Then +1 ≤ ⇒ −+1 ≥ − ⇒ 3 − +1 ≥ 3 − ⇒ +2 = 1 3 − +1 ≤ 1 3 − = +1. Also +2 0 [since 3 − +1 is positive] and +1 ≤ 2 by the induction hypothesis, so +1 is true. To find the limit, we use the fact that lim →∞ = lim →∞ +1 ⇒ = 3 −1 ⇒ 2 − 3 + 1 = 0 ⇒ = 3 ± √5 2 . But ≤ 2, so we must have = 3 −2√5 . 83. (a) Let be the number of rabbit pairs in the nth month. Clearly 1 = 1 = 2. In the nth month, each pair that is 2 or more months old (that is, −2 pairs) will produce a new pair to add to the −1 pairs already present. Thus, = −1 + −2, so that {} = {}, the Fibonacci sequence. (b) = +1 ⇒ −1 = −1 = −1 + −2 −1 = 1 + − −2 1 = 1 + −1 1/−2 = 1 + 1−2 . If = lim →∞, then = lim →∞ −1 and = lim →∞ −2, so must satisfy = 1 + 1 ⇒ 2 − − 1 = 0 ⇒ = 1 +2√5 [since must be positive]. 84. (a) If is continuous, then () = lim →∞ = lim →∞() = lim →∞+1 = lim →∞ = by Exercise 70(a). (b) By repeatedly pressing the cosine key on the calculator (that is, taking cosine of the previous answer) until the displayed value stabilizes, we see that ≈ 073909. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.1 SEQUENCES ¤ 967 85. (a) From the graph, it appears that the sequence 5! converges to 0, that is, lim →∞ 5 ! = 0. (b) From the first graph, it seems that the smallest possible value of corresponding to = 01 is 9, since 5! 01 whenever ≥ 10, but 959! 01. From the second graph, it seems that for = 0001, the smallest possible value for is 11 since 5! 0001 whenever ≥ 12. 86. Let 0 and let be any positive integer larger than ln()ln||. If , then ln()ln|| ⇒ ln|| ln [since || 1 ⇒ ln|| 0] ⇒ ln(||) ln ⇒ || ⇒ | − 0| , and so by Definition 2, lim →∞ = 0. 87. Theorem 6: If lim →∞ || = 0 then lim →∞ − || = 0, and since − || ≤ ≤ ||, we have that lim →∞ = 0 by the Squeeze Theorem. 88. Theorem 7: If lim →∞ = and the function is continuous at , then lim →∞ () = (). Proof: We must show that, given a number 0, there is an integer such that |() − ()| whenever . Suppose 0. Since is continuous at , there is a number 0 such that |() − ()| if | − | . Since lim →∞ = , there is an integer such that | − | if . Suppose . Then 0 | − | , so |() − ()| . 89. To Prove: If lim →∞ = 0 and {} is bounded, then lim →∞ () = 0. Proof: Since {} is bounded, there is a positive number such that || ≤ and hence, || || ≤ || for all ≥ 1. Let 0 be given. Since lim →∞ = 0, there is an integer such that | − 0| if . Then | − 0| = || = || || ≤ || = | − 0| · = for all . Since was arbitrary, lim →∞ () = 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 968 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 90. (a) +1 − +1 − = + −1 + −22 + −33 + · · · + −1 + + −1 + −22 + −33 + · · · + −1 + = ( + 1) (b) Since − 0, we have +1 − +1 ( + 1)( − ) ⇒ +1 − ( + 1)( − ) +1 ⇒ [( + 1) − ] +1. (c) With this substitution, ( + 1) − = 1, and so = 1 + 1 +1 = 1 + + 1 1 +1. (d) With this substitution, we get 1 + 211 2 1 ⇒ 1 + 21 2 ⇒ 1 + 212 4. (e) 2 since {} is increasing, so 2 4. (f) Since {} is increasing and bounded above by 4, 1 ≤ ≤ 4, and so {} is bounded and monotonic, and hence has a limit by the Monotonic Sequence Theorem. 91. (a) First we show that 1 1 . 1 − 1 = + 2 − √ = 1 2 − 2√ + = 1 2√ − √2 0 [since ] ⇒ 1 1. Also − 1 = − 1 2( + ) = 1 2( − ) 0 and − 1 = − √ = √√ − √ 0, so 1 1 . In the same way we can show that 1 2 2 1 and so the given assertion is true for = 1. Suppose it is true for = , that is, +1 +1 . Then +2 − +2 = 1 2(+1 + +1) − +1+1 = 1 2+1 − 2+1+1 + +1 = 1 2√+1 − +12 0, +1 − +2 = +1 − 1 2(+1 + +1) = 1 2(+1 − +1) 0, and +1 − +2 = +1 − +1+1 = +1 +1 − √+1 0 ⇒ +1 +2 +2 +1, so the assertion is true for = + 1. Thus, it is true for all by mathematical induction. (b) From part (a) we have +1 +1 , which shows that both sequences, {} and {}, are monotonic and bounded. So they are both convergent by the Monotonic Sequence Theorem. (c) Let lim →∞ = and lim →∞ = . Then lim →∞ +1 = lim →∞ + 2 ⇒ = + 2 ⇒ 2 = + ⇒ = . 92. (a) Let 0. Since lim →∞ 2 = , there exists 1 such that |2 − | for 1. Since lim →∞ 2+1 = , there exists 2 such that |2+1 − | for 2. Let = max{2122 + 1} and let . If is even, then = 2 where 1, so | − | = |2 − | . If is odd, then = 2 + 1, where 2, so | − | = |2+1 − | . Therefore lim →∞ = . (b) 1 = 1, 2 = 1 + 1 + 1 1 = 3 2 = 15, 3 = 1 + 512 = 7 5 = 14, 4 = 1 + 1215 = 17 12 = 1416, 5 = 1 + 1 2912 = 41 29 ≈ 1413793, 6 = 1 + 70129 = 99 70 ≈ 1414286, 7 = 1 + 169170 = 239 169 ≈ 1414201, °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.1 SEQUENCES ¤ 969 8 = 1 + 4081169 = 577 408 ≈ 1414216. Notice that 1 3 5 7 and 2 4 6 8. It appears that the odd terms are increasing and the even terms are decreasing. Let’s prove that 2−2 2 and 2−1 2+1 by mathematical induction. Suppose that 2−2 2. Then 1 + 2−2 1 + 2 ⇒ 1 1 + 2−2 1 1 + 2 ⇒ 1 + 1 1 + 2−2 1 + 1 1 + 2 ⇒ 2−1 2+1 ⇒ 1 + 2−1 1 + 2+1 ⇒ 1 1 + 2−1 1 1 + 2+1 ⇒ 1 + 1 1 + 2−1 1 + 1 1 + 2+1 ⇒ 2 2+2. We have thus shown, by induction, that the odd terms are increasing and the even terms are decreasing. Also all terms lie between 1 and 2, so both {} and {} are bounded monotonic sequences and are therefore convergent by the Monotonic Sequence Theorem. Let lim →∞ 2 = . Then lim →∞ 2+2 = also. We have +2 = 1 + 1 1 + 1 + 1(1 + ) = 1 + (3 + 2)1(1 + ) = 4 + 3 3 + 2 so 2+2 = 4 + 32 3 + 22 . Taking limits of both sides, we get = 4 + 3 3 + 2 ⇒ 3 + 22 = 4 + 3 ⇒ 2 = 2 ⇒ = √2 [since 0]. Thus, lim →∞ 2 = √2. Similarly we find that lim →∞ 2+1 = √2. So, by part (a), lim →∞ = √2. 93. (a) Suppose {} converges to . Then +1 = + ⇒ lim →∞ +1 = lim →∞ + lim →∞ ⇒ = + ⇒ 2 + = ⇒ ( + − ) = 0 ⇒ = 0 or = − . (b) +1 = + = 1 + since 1 + 1. (c) By part (b), 1 0, 2 1 2 0, 3 2 3 0, etc. In general, 0, so lim →∞ ≤ lim →∞ · 0 = 0 since . By (7) lim →∞ = 0 if − 1 1. Here = ∈ (01). (d) Let . We first show, by induction, that if 0 − , then − and +1 . For = 0, we have 1 − 0 = 0 + 0 − 0 = 0( − − 0) + 0 0 since 0 − . So 1 0. Now we suppose the assertion is true for = , that is, − and +1 . Then − − +1 = − − + = ( − ) + − − + = ( − − ) + 0 because − . So +1 − . And +2 − +1 = +1 + +1 − +1 = +1( − − +1) + +1 0 since +1 − . Therefore, +2 +1. Thus, the assertion is true for = + 1. It is therefore true for all by mathematical induction. A similar proof by induction shows that if 0 − , then − and {} is decreasing. In either case the sequence {} is bounded and monotonic, so it is convergent by the Monotonic Sequence Theorem. It then follows from part (a) that lim →∞ = − . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 970 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES LABORATORY PROJECT Logistic Sequences 1. To write such a program in Maple it is best to calculate all the points first and then graph them. One possible sequence of commands [taking 0 = 1 2 and = 15 for the difference equation] is t:=’t’;p(0):=1/2;k:=1.5; for j from 1 to 20 do p(j):=k*p(j-1)*(1-p(j-1)) od; plot([seq([t,p(t)] t=0..20)],t=0..20,p=0..0.5,style=point); In Mathematica, we can use the following program: p[0]=1/2 k=1.5 p[j_]:=k*p[j-1]*(1-p[j-1]) P=Table[p[t],{t,20}] ListPlot[P] With 0 = 1 2 and = 15: 0 05 7 03338465076 14 03333373303 1 0375 8 03335895255 15 03333353318 2 03515625 9 03334613309 16 03333343326 3 03419494629 10 03333973076 17 03333338329 4 03375300416 11 03333653143 18 03333335831 5 03354052689 12 03333493223 19 03333334582 6 03343628617 13 03333413274 20 03333333958 With 0 = 1 2 and = 25: 0 05 7 06004164790 14 05999967417 1 0625 8 05997913269 15 06000016291 2 05859375 9 06001042277 16 05999991854 3 06065368651 10 05999478590 17 06000004073 4 05966247409 11 06000260637 18 05999997964 5 06016591486 12 05999869664 19 06000001018 6 05991635437 13 06000065164 20 05999999491 Both of these sequences seem to converge the first to about 1 3, the second to about 0.60. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE LABORATORY PROJECT LOGISTIC SEQUENCES ¤ 971 With 0 = 7 8 and = 15: 0 0875 7 03239166554 14 03332554829 1 01640625 8 03284919837 15 03332943990 2 02057189941 9 03308775005 16 03333138639 3 02450980344 10 03320963702 17 03333235980 4 02775374819 11 03327125567 18 03333284655 5 03007656421 12 03330223670 19 03333308994 6 03154585059 13 03331777051 20 03333321164 With 0 = 7 8 and = 25: 0 0875 7 06016572368 14 05999869815 1 02734375 8 05991645155 15 06000065088 2 04966735840 9 06004159972 16 05999967455 3 06249723374 10 05997915688 17 06000016272 4 05859547872 11 06001041070 18 05999991864 5 06065294364 12 05999479194 19 06000004068 6 05966286980 13 06000260335 20 05999997966 The limit of the sequence seems to depend on , but not on 0. 2. With 0 = 7 8 and = 32: 0 0875 7 05830728495 14 07990633827 1 035 8 07779164854 15 05137954979 2 0728 9 05528397669 16 07993909896 3 06336512 10 07910654689 17 05131681132 4 07428395416 11 05288988570 18 07994451225 5 06112926626 12 07973275394 19 05130643795 6 07603646184 13 05171082698 20 07994538304 It seems that eventually the terms fluctuate between two values (about 05 and 08 in this case). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 972 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 3. With 0 = 7 8 and = 342: 0 0875 7 04523028596 14 08442074951 1 03740625 8 08472194412 15 04498025048 2 08007579316 9 04426802161 16 08463823232 3 05456427596 10 08437633929 17 04446659586 4 08478752457 11 04508474156 18 08445284520 5 04411212220 12 08467373602 19 04490464985 6 08431438501 13 04438243545 20 08461207931 With 0 = 7 8 and = 345: 0 0875 7 04670259170 14 08403376122 1 037734375 8 08587488490 15 04628875685 2 08105962830 9 04184824586 16 08577482026 3 05296783241 10 08395743720 17 04209559716 4 08594612299 11 04646778983 18 08409445432 5 04167173034 12 08581956045 19 04614610237 6 08385707740 13 04198508858 20 08573758782 From the graphs above, it seems that for between 34 and 35, the terms eventually fluctuate between four values. In the graph below, the pattern followed by the terms is 0395083204870869 0395 . Note that even for = 342 (as in the first graph), there are four distinct “branches”; even after 1000 terms, the first and third terms in the pattern differ by about 2 × 10−9, while the first and fifth terms differ by only 2 × 10−10. With 0 = 7 8 and = 348: °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.2 SERIES ¤ 973 4. 0 = 05, = 37 0 = 0501, = 37 0 = 075, = 39 0 = 0749, = 39 0 = 05, = 3999 From the graphs, it seems that if 0 is changed by 0001, the whole graph changes completely. (Note, however, that this might be partially due to accumulated round-off error in the CAS. These graphs were generated by Maple with 100-digit accuracy, and different degrees of accuracy give different graphs.) There seem to be some some fleeting patterns in these graphs, but on the whole they are certainly very chaotic. As increases, the graph spreads out vertically, with more extreme values close to 0 or 1. 11.2 Series 1. (a) A sequence is an ordered list of numbers whereas a series is the sum of a list of numbers. (b) A series is convergent if the sequence of partial sums is a convergent sequence. A series is divergent if it is not convergent. 2. ∞ =1 = 5 means that by adding sufficiently many terms of the series we can get as close as we like to the number 5. In other words, it means that lim→∞ = 5, where is the th partial sum, that is, =1 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 974 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 3. ∞ =1 = lim →∞ = lim →∞ [2 − 3(08)] = lim →∞ 2 − 3 lim →∞ (08) = 2 − 3(0) = 2 4. ∞ =1 = lim →∞ = lim →∞ 2 − 1 42 + 1 = lim →∞ (4 (22−+ 1) 1) 22 = lim →∞ 1 4 + 1 − 1 2 2 = 14 + 0 − 0 = 1 4 5. For ∞ =1 1 4 + 2 , = 1 4 + 2 . 1 = 1 = 1 14 + 12 = 1 2 = 05, 2 = 1 + 2 = 1 2 + 1 16 + 4 = 055, 3 = 2 + 3 ≈ 05611, 4 = 3 + 4 ≈ 05648, 5 = 4 + 5 ≈ 05663, 6 = 5 + 6 ≈ 05671, 7 = 6 + 7 ≈ 05675, and 8 = 7 + 8 ≈ 05677. It appears that the series is convergent. 6. For ∞ =1 1 √3 , = 1 √3 . 1 = 1 = 1 √3 1 = 1, 2 = 1 + 2 = 1 + √312 ≈ 17937, 3 = 2 + 3 ≈ 24871, 4 = 3 + 4 ≈ 31170, 5 = 4 + 5 ≈ 37018, 6 = 5 + 6 ≈ 42521, 7 = 6 + 7 ≈ 47749, and 8 = 7 + 8 ≈ 52749. It appears that the series is divergent. 7. For ∞ =1 sin, = sin. 1 = 1 = sin 1 ≈ 08415, 2 = 1 + 2 ≈ 17508, 3 = 2 + 3 ≈ 18919, 4 = 3 + 4 ≈ 11351, 5 = 4 + 5 ≈ 01762, 6 = 5 + 6 ≈ −01033, 7 = 6 + 7 ≈ 05537, and 8 = 7 + 8 ≈ 15431. It appears that the series is divergent. 8. For ∞ =1 (−1)−1 ! , = (−1)−1 1!. 1 = 1 = 1! 1 = 1, 2 = 1 + 2 = 1 − 2! 1 = 05, 3 = 2 + 3 = 05 + 1 3! ≈ 06667, 4 = 3 + 4 = 0625, 5 = 4 + 5 ≈ 06333, 6 = 5 + 6 ≈ 06319, 7 = 6 + 7 ≈ 06321, and 8 = 7 + 8 ≈ 06321. It appears that the series is convergent. 9. 1 −240000 2 −192000 3 −201600 4 −199680 5 −200064 6 −199987 7 −200003 8 −199999 9 −200000 10 −200000 From the graph and the table, it seems that the series converges to −2. In fact, it is a geometric series with = −24 and = − 1 5, so its sum is ∞ =1 12 (−5) = −24 1 − − 1 5 = −24 12 = −2 Note that the dot corresponding to = 1 is part of both {} and {}. TI-86 Note: To graph {} and {}, set your calculator to Param mode and DrawDot mode. (DrawDot is under GRAPH, MORE, FORMT (F3).) Now under E(t)= make the assignments: xt1=t, yt1=12/(-5)ˆt, xt2=t, yt2=sum seq(yt1,t,1,t,1). (sum and seq are under LIST, OPS (F5), MORE.) Under WIND use 1,10,1,0,10,1,-3,1,1 to obtain a graph similar to the one above. Then use TRACE (F4) to see the values. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.2 SERIES ¤ 975 10. 1 054030 2 012416 3 −086584 4 −151948 5 −123582 6 −027565 7 047825 8 033275 9 −057838 10 −141745 The series ∞ =1 cos diverges, since its terms do not approach 0. 11. 1 044721 2 115432 3 198637 4 288080 5 380927 6 475796 7 571948 8 668962 9 766581 10 864639 The series ∞ =1 √2 + 4 diverges, since its terms do not approach 0. 12. 1 490000 2 833000 3 1073100 4 1241170 5 1358819 6 1441173 7 1498821 8 1539175 9 1567422 10 1587196 From the graph and the table, we see that the terms are getting smaller and may approach 0, and that the series approaches a value near 16. The series is geometric with 1 = 49 and = 07, so its sum is ∞ =1 7+1 10 = 49 1 − 07 = 49 03 = 163. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 976 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 13. 2 100000 3 133333 4 150000 5 160000 6 166667 7 171429 8 175000 9 177778 10 180000 11 181818 From the graph and the table, we see that the terms are getting smaller and may approach 0, and that the series may approach a number near 2. Using partial fractions, we have =2 2 2 − = =2 −2 1 − 2 = 21 − 22 + 2 2 − 2 3 + 2 3 − 2 4 +· · · + −2 2 − −2 1 + −2 1 − 2 = 2 − 2 As → ∞, 2 − 2 → 2, so ∞ =2 2 2 − = 2. 14. 1 036205 2 051428 3 059407 4 064280 5 067557 6 069910 7 071680 8 073059 9 074164 10 075069 From the graph and the table, we see that the terms are getting smaller and may approach 0, and that the series may approach a number near 1. =1 sin 1 − sin + 1 1 = sin 1 − sin 12 + sin 1 2 − sin 1 3 +· · · + sin −1 1 + sin 1 +sin 1 − sin + 1 1 = sin 1 − sin 1 + 1 As → ∞, sin 1 − sin 1 + 1 → sin 1 − sin 0 = sin 1, so ∞ =1 sin 1 − sin + 1 1 = sin 1 ≈ 084147. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.2 SERIES ¤ 977 15. (a) lim →∞ = lim →∞ 2 3 + 1 = 2 3 , so the sequence {} is convergent by (11.1.1). (b) Since lim →∞ = 2 3 6= 0, the series ∞ =1 is divergent by the Test for Divergence. 16. (a) Both =1 and =1 represent the sum of the first terms of the sequence {}, that is, the th partial sum. (b) =1 = + + · · · + terms = , which, in general, is not the same as =1 = 1 + 2 + · · · + . 17. 3 − 4 + 16 3 − 64 9 + · · · is a geometric series with ratio = − 4 3. Since || = 4 3 1, the series diverges. 18. 4 + 3 + 9 4 + 27 16 + · · · is a geometric series with ratio 3 4. Since || = 3 4 1, the series converges to 1 − = 1 −434 = 16. 19. 10 − 2 + 04 − 008 + · · · is a geometric series with ratio − 10 2 = − 1 5. Since || = 1 5 1, the series converges to 1 − = 10 1 − (−15) = 10 65 = 50 6 = 25 3 . 20. 2 + 05 + 0125 + 003125 + · · · is a geometric series with ratio = 025 = 1 4. Since || = 1 4 1, the series converges to 1 − = 2 1 − 14 = 2 34 = 8 3 . 21. ∞ =1 12 (0.73)−1 is a geometric series with first term = 12 and ratio = 073. Since || = 073 1, the series converges to 1 − = 12 1 − 073 = 12 027 = 12(100) 27 = 400 9 . 22. ∞ =1 5 = 5 ∞ =1 1 . The latter series is geometric with = 1 and ratio = 1 . Since || = 1 1, it converges to 1 1 − 1 = 1 − 1 . Thus, the given series converges to 5 −1 1 = −5 1. 23. ∞ =1 (−3)−1 4 = 1 4 ∞ =1−34−1. The latter series is geometric with = 1 and ratio = − 3 4. Since || = 3 4 1, it converges to 1 1 − (−34) = 4 7 . Thus, the given series converges to 1 4 4 7 = 1 7. 24. ∞ =0 3+1 (−2) = 3 ∞ =0 − 3 2 is a geometric series with ratio = − 3 2. Since || = 3 2 1, the series diverges. 25. ∞ =1 2 6−1 = ∞ =1 (2) 66−1 = 6 ∞ =1 62 is a geometric series with ratio = 62 . Since || = 62 [≈ 123] 1, the series diverges. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 978 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 26. ∞ =1 6 · 22−1 3 = ∞ =1 6(22) · 2−1 3 = 3 ∞ =1 4 3 is a geometric series with ratio = 43. Since || = 4 3 1, the series diverges. 27. 1 3 + 1 6 + 1 9 + 1 12 + 1 15 + · · · = ∞ =1 1 3 = 1 3 ∞ =1 1 . This is a constant multiple of the divergent harmonic series, so it diverges. 28. 1 3 + 2 9 + 27 1 + 81 2 + 243 1 + 729 2 + · · · = 1 3 + 27 1 + 243 1 + · · · + 2 9 + 81 2 + 729 2 + · · ·, which are both convergent geometric series with sums 13 1 − 19 = 3 8 and 29 1 − 19 = 1 4 , so the original series converges and its sum is 3 8 + 1 4 = 5 8. 29. ∞ =1 2 + 1 − 2 diverges by the Test for Divergence since lim →∞ = lim →∞ 2 + 1 − 2 = lim →∞ 2 + 1 1 − 2 = − 1 2 6= 0. 30. ∞ =1 2 2 − 2 + 5 diverges by the Test for Divergence since lim →∞ 2 −22 + 5 = lim →∞ 1 − 21+ 52 = 1 6= 0. 31. ∞ =1 3+14− = ∞ =1 3 · 31 4 = 3 ∞ =13 4. The latter series is geometric with = 34 and ratio = 34. Since || = 3 4 1, it converges to 34 1 − 34 = 3. Thus, the given series converges to 3(3) = 9. 32. ∞ =1 [(−02) + (06)−1] = ∞ =1 (−02) + ∞ =1 (06)−1 [sum of two geometric series] = −02 1 − (−02) + 1 1 − 06 = − 1 6 + 5 2 = 7 3 33. ∞ =1 1 4 + − diverges by the Test for Divergence since lim →∞ 4 +1− = 4 + 0 1 = 1 4 6= 0. 34. ∞ =1 2 + 4 diverges by the Test for Divergence since lim →∞ 2 + 4 = lim →∞2 + 4 ≥ lim →∞4 = ∞ since 4 1. 35. ∞ =1 (sin 100) is a geometric series with first term = sin 100 [≈ −0506] and ratio = sin 100. Since || 1, the series converges to sin 100 1 − sin 100 ≈ −0336. 36. ∞ =1 1 1 +2 3 diverges by the Test for Divergence since lim →∞ 1 +12 3 = 1 + 0 1 = 1 6= 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.2 SERIES ¤ 979 37. ∞ =1 ln222+ 1 + 1 diverges by the Test for Divergence since lim →∞ = lim →∞ ln222+ 1 + 1 = lnlim →∞ 222+ 1 + 1 = ln 1 2 6= 0. 38. ∞ =0 (√2)− = ∞ =0 √12 is a geometric series with first term = √120 = 1 and ratio = √12. Since || 1, the series converges to 1 1 − 1√2 = √2 √2 − 1 ≈ 3414. 39. ∞ =1 arctan diverges by the Test for Divergence since lim →∞ = lim →∞ arctan = 2 6= 0. 40. ∞ =1 53 + 2 diverges because ∞=1 2 = 2 ∞=1 1 diverges. (If it converged, then 12 · 2 ∞=1 1 would also converge by Theorem 8(i), but we know from Example 9 that the harmonic series ∞ =1 1 diverges.) If the given series converges, then the difference ∞ =1 53 + 2 − ∞=1 53 must converge (since ∞=1 53 is a convergent geometric series) and equal ∞=1 2 , but we have just seen that ∞ =1 2 diverges, so the given series must also diverge. 41. ∞ =1 1 = ∞ =1 1 is a geometric series with first term = 1 and ratio = 1 . Since || = 1 1, the series converges to 1 1 − 1 = 1 1 − 1 · = 1 − 1 . By Example 8, ∞ =1 1 ( + 1) = 1. Thus, by Theorem 8(ii), ∞ =1 1 + (1+ 1) = ∞=1 1 + ∞=1 (1+ 1) = −1 1 + 1 = −1 1 + −− 11 = − 1. 42. ∞ =1 2 diverges by the Test for Divergence since lim →∞ = lim →∞ 2 = lim →∞ 2 = lim H →∞ 2 = lim H →∞ 2 = ∞ 6= 0. 43. Using partial fractions, the partial sums of the series ∞ =2 2 2 − 1 are = =2 2 ( − 1)( + 1) = =2 −1 1 − + 1 1 = 1 − 13 + 1 2 − 1 4 + 1 3 − 1 5 + ··· + −1 3 − −1 1 + −1 2 − 1 This sum is a telescoping series and = 1 + 1 2 − 1 − 1 − 1 . Thus, ∞ =2 2 2 − 1 = lim →∞ = lim →∞1 + 12 − −1 1 − 1 = 32. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 980 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 44. For the series ∞ =1 ln + 1, = (ln 1 − ln 2) + (ln 2 − ln 3) + (ln 3 − ln 4) + · · · + [ln − ln( + 1)] = ln 1 − ln( + 1) = −ln( + 1) [telescoping series] Thus, lim →∞ = −∞, so the series is divergent. 45. For the series ∞ =1 3 ( + 3), = =1 3 ( + 3) = =11 − + 3 1 [using partial fractions]. The latter sum is 1 − 1 4 + 1 2 − 1 5 + 1 3 − 1 6 + 1 4 − 1 7 + · · · + −1 3 − 1 + 1−2 − + 1 1 + −1 1 − +2 1 + 1 − +3 1 = 1 + 1 2 + 1 3 − 1+1 − + 2 1 − +3 1 [telescoping series] Thus, ∞ =1 3 ( + 3) = lim →∞ = lim →∞1 + 1 2 + 1 3 − 1+1 − + 2 1 − +3 1 = 1 + 1 2 + 1 3 = 11 6 . Converges 46. For the series ∞ =4 √1 − √1+ 1 = =4 √1 − √1+ 1 = √14 − √15 + √15 − √16 + · · · + √1 − √1+ 1 = √14 − √1+ 1 [telescoping series] Thus, ∞ =4 √1 − √1+ 1 = lim →∞ = lim →∞√14 − √1+ 1 = √14 − 0 = 1 2. Converges 47. For the series ∞ =1 1 − 1(+1), = =1 1 − 1(+1) = (1 − 12) + (12 − 13) + · · · + 1 − 1(+1) = − 1(+1) [telescoping series] Thus, ∞ =1 1 − 1(+1) = lim →∞ = lim →∞ − 1(+1) = − 0 = − 1. Converges 48. Using partial fractions, the partial sums of the series ∞ =2 1 3 − are = =2 1 ( − 1)( + 1) = =2 −1 + 1−21 + 1+ 1 2 = 12 =2 −1 1 − 2 + + 1 1 = 1 2 11 − 22 + 1 3 + 21 − 2 3 + 1 4 + 1 3 − 2 4 + 15 + 1 4 − 2 5 + 1 6 + · · · + −1 3 − −2 2 + −1 1 + −1 2 − −2 1 + 1 + −1 1 − 2 + + 1 1 Note: In three consecutive expressions in parentheses, the 3rd term in the first expression plus the 2nd term in the second expression plus the 1st term in the third expression sum to 0. = 1 2 11 − 22 + 21 + 1 − 2 + + 1 1 = 14 − 21 + 21+ 2 Thus, ∞ =2 1 3 − = lim →∞ = lim →∞1 4 − 21 + 21+ 2 = 14. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.2 SERIES ¤ 981 49. (a) Many people would guess that 1, but note that consists of an infinite number of 9s. (b) = 099999 = 9 10 + 9 100 + 9 1000 + 9 10,000 + · · · = ∞ =1 9 10 , which is a geometric series with 1 = 09 and = 01. Its sum is 09 1 − 01 = 09 09 = 1, that is, = 1. (c) The number 1 has two decimal representations, 100000 and 099999 . (d) Except for 0, all rational numbers that have a terminating decimal representation can be written in more than one way. For example, 05 can be written as 049999 as well as 050000 . 50. 1 = 1, = (5 − )−1 ⇒ 2 = (5 − 2)1 = 3(1) = 3, 3 = (5 − 3)2 = 2(3) = 6, 4 = (5 − 4)3 = 1(6) = 6, 5 = (5 − 5)4 = 0, and all succeeding terms equal 0. Thus, ∞ =1 = 4 =1 = 1 + 3 + 6 + 6 = 16. 51. 08 = 8 10 + 8 102 + · · · is a geometric series with = 10 8 and = 10 1 . It converges to 1 − = 1 −8110 10 = 89. 52. 046 = 46 100 + 46 1002 + · · · is a geometric series with = 100 46 and = 100 1 . It converges to 1 − = 146 −1100 100 = 46 99. 53. 2516 = 2 + 516 103 + 516 106 + · · · . Now 516 103 + 516 106 + · · · is a geometric series with = 516 103 and = 10 13 . It converges to 1 − = 516103 1 − 1103 = 516103 999103 = 516 999 . Thus, 2516 = 2 + 516 999 = 2514 999 = 838 333 . 54. 10135 = 101 + 35 103 + 35 105 + · · · . Now 10 353 + 10 355 + · · · is a geometric series with = 10 353 and = 10 12 . It converges to 1 − = 35103 1 − 1102 = 35103 99102 = 35 990 . Thus, 10135 = 101 + 35 990 = 9999 + 35 990 = 10,034 990 = 5017 495 . 55. 1234567 = 1234 + 567 106 + 567 109 + · · · . Now 567 106 + 567 109 + · · · is a geometric series with = 567 106 and = 1 103 . It converges to 1 − = 1567 − 110 1063 = 567 999 10 106 3 = 999 567 ,000 = 3721 ,000. Thus, 1234567 = 1234 + 21 37,000 = 1234 1000 + 21 37,000 = 45,658 37,000 + 21 37,000 = 45,679 37,000. 56. 571358 = 5 + 71,358 105 + 71,358 1010 + · · · . Now 7110 ,358 5 + 71 10,358 10 + · · · is a geometric series with = 7110 ,358 5 and = 1 105 . It converges to 1 − = 71 1 −,358 110 1055 = 71 99,,358 99910 105 5 = 71 99,,358 999 = 23 33,,786 333. Thus, 571358 = 5 + 23,786 33,333 = 166,665 33,333 + 23,786 33,333 = 190,451 33,333 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 982 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 57. ∞ =1 (−5) = ∞ =1 (−5) is a geometric series with = −5, so the series converges ⇔ || 1 ⇔ |−5| 1 ⇔ || 1 5, that is, − 1 5 1 5. In that case, the sum of the series is 1 − = 1 −−(5−5) = 1 + 5 −5. 58. ∞ =1 ( + 2) is a geometric series with = + 2, so the series converges ⇔ || 1 ⇔ | + 2| 1 ⇔ −1 + 2 1 ⇔ −3 −1. In that case, the sum of the series is 1 − = + 2 1 − ( + 2) = + 2 − − 1 . 59. ∞ =0 ( − 2) 3 = ∞ =0 −3 2 is a geometric series with = −3 2, so the series converges ⇔ || 1 ⇔ − 2 3 1 ⇔ −1 − 2 3 1 ⇔ −3 − 2 3 ⇔ −1 5. In that case, the sum of the series is 1 − = 1 1 − − 2 3 = 1 3 − ( − 2) 3 = 3 5 − . 60. ∞ =0 (−4)( − 5) = ∞ =0 [−4( − 5)] is a geometric series with = −4( − 5), so the series converges ⇔ || 1 ⇔ |−4( − 5)| 1 ⇔ | − 5| 1 4 ⇔ − 1 4 − 5 1 4 ⇔ 19 4 21 4 . In that case, the sum of the series is 1 − = 1 1 − [−4( − 5)] = 1 4 − 19. 61. ∞ =0 2 = ∞ =0 2 is a geometric series with = 2, so the series converges ⇔ || 1 ⇔ 2 1 ⇔ 2 || ⇔ 2 or −2. In that case, the sum of the series is 1 − = 1 1 − 2 = − 2 . 62. ∞ =0 sin 3 = ∞ =0sin3 is a geometric series with = sin3, so the series converges ⇔ || 1 ⇔ sin 3 1 ⇔ |sin| 3, which is true for all . Thus, the sum of the series is 1 − = 1 1 − (sin)3 = 3 3 − sin . 63. ∞ =0 = ∞ =0 () is a geometric series with = , so the series converges ⇔ || 1 ⇔ || 1 ⇔ −1 1 ⇔ 0 1 ⇔ 0. In that case, the sum of the series is 1 − = 1 1 − . 64. Because 1 → 0 and ln is continuous, we have lim →∞ ln1 + 1 = ln 1 = 0. We now show that the series ∞ =1 ln1 + 1 = ∞=1 ln + 1 = ∞=1[ln( + 1) − ln] diverges. = (ln 2 − ln 1) + (ln 3 − ln 2) + · · · + (ln( + 1) − ln) = ln( + 1) − ln 1 = ln( + 1) As → ∞, = ln( + 1) → ∞, so the series diverges. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.2 SERIES ¤ 983 65. After defining , We use convert(f,parfrac); in Maple, Apart in Mathematica, or Expand Rational and Simplify in Derive to find that the general term is 32 + 3 + 1 (2 + )3 = 1 3 − 1 ( + 1)3 . So the nth partial sum is = =113 − ( + 1) 1 3 = 1 − 213 + 213 − 313 + · · · + 13 − ( + 1) 1 3 = 1 − ( + 1) 1 3 The series converges to lim →∞ = 1. This can be confirmed by directly computing the sum using sum(f,n=1..infinity); (in Maple), Sum[f,{n,1,Infinity}] (in Mathematica), or Calculus Sum (from 1 to ∞) and Simplify (in Derive). 66. See Exercise 65 for specific CAS commands. 1 5 − 53 + 4 = 1 24( − 2) + 1 24( + 2) − 1 6( − 1) − 1 6( + 1) + 1 4. So the th partial sum is = 1 24 =3 −1 2 − −4 1 + 6 − + 1 4 + + 2 1 = 1 2411 − 24 + 6 3 − 4 4 + 1 5 + · · · + −1 2 − −4 1 + 6 − + 1 4 + + 2 1 The terms with denominator 5 or greater cancel, except for a few terms with in the denominator. So as → ∞, → 1 2411 − 23 + 3 3 − 1 4 = 24 1 1 4 = 96 1 . 67. For = 1, 1 = 0 since 1 = 0. For 1, = − −1 = − 1 + 1 − ( − 1) − 1 ( − 1) + 1 = ( − 1) − ( + 1)( − 2) ( + 1) = 2 ( + 1) Also, ∞ =1 = lim →∞ = lim →∞ 1 − 1 1 + 1 = 1. 68. 1 = 1 = 3 − 1 2 = 5 2 . For 6= 1, = − −1 = 3 − 2− − 3 − ( − 1)2−(−1) = −2 + 2−−11 · 22 = 2(2− 1) − 2 = 2− 2 Also, ∞ =1 = lim →∞ = lim →∞3 − 2 = 3 because lim →∞ 2 = lim H →∞ 21ln 2 = 0. 69. (a) The quantity of the drug in the body after the first tablet is 100 mg. After the second tablet, there is 100 mg plus 20% of the first 100-mg tablet; that is, 100 + 020(100) = 120 mg. After the third tablet, the quantity is 100 + 020(120) or, equivalently, 100 + 100(020) + 100(020)2. Either expression gives us 124 mg. (b) From part (a), we see that +1 = 100 + 020. (c) = 100 + 100(020)1 + 100(020)2 + · · · + 100(020)−1 = =1 100(020)−1 [geometric with = 100 and = 020]. The quantity of the antibiotic that remains in the body in the long run is lim →∞ = 100 1 − 020 = 100 45 = 125 mg. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 984 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 70. (a) The concentration of the drug after the first injection is 15 mgL. “Reduced by 90%” is the same as 10% remains, so the concentration after the second injection is 15 + 010(15) = 165 mgL. The concentration after the third injection is 15 + 010(165), or, equivalently, 15 + 15(010) + 15(010)2. Either expression gives us 1665 mgL. (b) = 15 + 15(010)1 + 15(010)2 + · · · + 15(010)−1 = =1 15(010)−1 [geometric with = 15 and = 010]. By (3), = 15[1 − (010)] 1 − 010 = 15 09 [1 − (010)] = 5 3 [1 − (010)] mgL. (c) The limiting value of the concentration is lim →∞ = lim →∞ 5 3 [1 − (010)] = 5 3(1 − 0) = 5 3 mgL. 71. (a) The quantity of the drug in the body after the first tablet is 150 mg. After the second tablet, there is 150 mg plus 5% of the first 150-mg tablet, that is, [150 + 150(005)] mg. After the third tablet, the quantity is [150 + 150(005) + 150(005)2] = 157875 mg. After tablets, the quantity (in mg) is 150 + 150(005) + · · · + 150(005)−1. We can use Formula 3 to write this as 150(1 − 005) 1 − 005 = 3000 19 (1 − 005). (b) The number of milligrams remaining in the body in the long run is lim →∞ 3000 19 (1 − 005) = 3000 19 (1 − 0) ≈ 157895, only 002 mg more than the amount after 3 tablets. 72. (a) The residual concentration just before the second injection is − ; before the third, − + −2 ; before the ( + 1)st, − + −2 + · · · + − . This sum is equal to −1 − − 1 − − [Formula 3]. (b) The limiting pre-injection concentration is lim →∞ −1 − − 1 − − = −(1 − 0) 1 − − · = − 1. (c) − 1 ≥ ⇒ ≥ − 1, so the minimal dosage is = − 1. 73. (a) The first step in the chain occurs when the local government spends dollars. The people who receive it spend a fraction of those dollars, that is, dollars. Those who receive the dollars spend a fraction of it, that is, 2 dollars. Continuing in this way, we see that the total spending after transactions is = + + 2 + · · · + –1 = (1 − ) 1 − by (3). (b) lim →∞ = lim →∞ (1 − ) 1 − = 1 − lim →∞ (1 − ) = 1 − since 0 1 ⇒ lim →∞ = 0 = [since + = 1] = [since = 1] If = 08, then = 1 − = 02 and the multiplier is = 1 = 5. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.2 SERIES ¤ 985 74. (a) Initially, the ball falls a distance , then rebounds a distance , falls , rebounds 2, falls 2, etc. The total distance it travels is + 2 + 22 + 23 + · · · = 1 + 2 + 22 + 23 + · · · = 1 + 21 + + 2 + · · · = 1 + 21 −1 = 1 + 1 − meters (b) From Example 3 in Section 2.1, we know that a ball falls 1 22 meters in seconds, where is the gravitational acceleration. Thus, a ball falls meters in = 2 seconds. The total travel time in seconds is 2 + 22 + 22 2 + 22 3 + · · · = 2 1 + 2√ + 2√ 2 + 2√ 3 + · · · = 2 1 + 2√1 + √ + √ 2 + · · · = 2 1 + 2√1 −1√ = 2 1 + 1 − √√ (c) It will help to make a chart of the time for each descent and each rebound of the ball, together with the velocity just before and just after each bounce. Recall that the time in seconds needed to fall meters is 2. The ball hits the ground with velocity − 2 = −√2 (taking the upward direction to be positive) and rebounds with velocity 2 = √2, taking time 2 to reach the top of its bounce, where its velocity is 0. At that point, its height is 2. All these results follow from the formulas for vertical motion with gravitational acceleration −: 2 2 = − ⇒ = = 0 − ⇒ = 0 + 0 − 1 22. number of descent time of descent speed before bounce speed after bounce time of ascent peak height 1 2 √2 √2 2 2 2 22 22 22 22 4 3 24 24 24 24 6 · · · · · · · · · · · · · · · · · · The total travel time in seconds is 2 + 2 + 2 + 22 + 22 + · · · = 2 1 + 2 + 22 + 23 + · · · = 2 1 + 2(1 + + 2 + · · ·) = 2 1 + 21 −1 = 2 1 + 1 − Another method: We could use part (b). At the top of the bounce, the height is 2 = , so √ = and the result follows from part (b). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 986 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 75. ∞ =2 (1 + )− is a geometric series with = (1 + )−2 and = (1 + )−1, so the series converges when (1 + )−1 1 ⇔ |1 + | 1 ⇔ 1 + 1 or 1 + −1 ⇔ 0 or −2. We calculate the sum of the series and set it equal to 2: (1 + )−2 1 − (1 + )−1 = 2 ⇔ 1 +1 2 = 2 − 21 +1 ⇔ 1 = 2(1 + )2 − 2(1 + ) ⇔ 22 + 2 − 1 = 0 ⇔ = −2 ± √12 4 = ±√3 − 1 2 . However, the negative root is inadmissible because −2 −√32 − 1 0. So = √3 − 1 2 . 76. ∞ =0 = ∞ =0 () is a geometric series with = ()0 = 1 and = . If 1, it has sum 1 1 − , so 1 1 − = 10 ⇒ 1 10 = 1 − ⇒ = 10 9 ⇒ = ln 10 9 . 77. = 1+ 1 2 + 13 +···+ 1 = 11213 · · · 1 (1 + 1)1 + 1 2 1 + 1 3 · · · 1 + 1 [ 1 + ] = 2 1 3 2 4 3 · · · + 1 = + 1 Thus, + 1 and lim →∞ = ∞. Since {} is increasing, lim →∞ = ∞, implying that the harmonic series is divergent. 78. The area between = −1 and = for 0 ≤ ≤ 1 is 01(−1 − ) = − + 1 +1 1 0 = 1 − + 1 1 = ( + 1) − ( + 1) = 1 ( + 1) We can see from the diagram that as → ∞, the sum of the areas between the successive curves approaches the area of the unit square, that is, 1. So ∞ =1 1 ( + 1) = 1. 79. Let be the diameter of . We draw lines from the centers of the to the center of (or ), and using the Pythagorean Theorem, we can write 12 + 1 − 1 2 12 = 1 + 1 2 12 ⇔ 1 = 1 + 1 2 12 − 1 − 1 2 12 = 21 [difference of squares] ⇒ 1 = 1 2. Similarly, 1 = 1 + 1 2 22 − 1 − 1 − 1 2 22 = 22 + 21 − 2 1 − 12 = (2 − 1)(1 + 2) ⇔ °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.2 SERIES ¤ 987 2 = 1 2 − 1 − 1 = (12−−11)2 , 1 = 1 + 1 232 − 1 − 1 − 2 − 1 232 ⇔ 3 = [12−−((11++22)] )2 , and in general, +1 = 1 − =1 2 2 − =1 . If we actually calculate 2 and 3 from the formulas above, we find that they are 16 = 21· 3 and 1 12 = 1 3 · 4 respectively, so we suspect that in general, = (1+ 1). To prove this, we use induction: Assume that for all ≤ , = 1 ( + 1) = 1 − 1 + 1. Then =1 = 1 − 1 + 1 = + 1 [telescoping sum]. Substituting this into our formula for +1, we get +1 = 1 − + 1 2 2 − + 1 = 1 ( + 1)2 + 2 + 1 = 1 ( + 1)( + 2), and the induction is complete. Now, we observe that the partial sums =1 of the diameters of the circles approach 1 as → ∞; that is, ∞ =1 = ∞ =1 1 ( + 1) = 1, which is what we wanted to prove. 80. || = sin, || = || sin = sin2 , || = ||sin = sin3 , . Therefore, || + || + || + | | + · · · = ∞ =1 sin = 1 −sinsin since this is a geometric series with = sin and |sin| 1 because 0 2 . 81. The series 1 − 1 + 1 − 1 + 1 − 1 + · · · diverges (geometric series with = −1) so we cannot say that 0 = 1 − 1 + 1 − 1 + 1 − 1 + · · · . 82. If ∞ =1 is convergent, then lim →∞ = 0 by Theorem 6, so lim →∞ 1 6= 0, and so ∞ =1 1 is divergent by the Test for Divergence. 83. ∞ =1 = lim →∞ =1 = lim →∞ =1 = lim →∞ =1 = ∞ =1 , which exists by hypothesis. 84. If were convergent, then (1)() = would be also, by Theorem 8(i). But this is not the case, so must diverge. 85. Suppose on the contrary that ( + ) converges. Then ( + ) and are convergent series. So by Theorem 8(iii), [( + ) − ] would also be convergent. But [( + ) − ] = , a contradiction, since is given to be divergent. 86. No. For example, take = and = (−), which both diverge, yet ( + ) = 0, which converges with sum 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 988 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 87. The partial sums {} form an increasing sequence, since − −1 = 0 for all . Also, the sequence {} is bounded since ≤ 1000 for all . So by the Monotonic Sequence Theorem, the sequence of partial sums converges, that is, the series is convergent. 88. (a) RHS = 1 −1 − 1 +1 = +1 − −1 2−1+1 = +1 − −1 −1+1 = (−1 + ) − −1 −1+1 = 1 −1+1 = LHS (b) ∞ =2 1 −1+1 = ∞ =2−11 − 1+1 [from part (a)] = lim →∞ 112 − 213 + 213 − 314 + 314 − 415 + · · · + −11 − 1+1 = lim →∞112 − 1+1 = 112 − 0 = 11· 1 = 1 because → ∞ as → ∞. (c) ∞ =2 −1+1 = ∞ =2−1 − +1 [as above] = ∞ =21−1 − 1+1 = lim →∞ 11 − 13 + 12 − 14 + 13 − 15 + 14 − 16 + · · · + 1−1 − 1+1 = lim →∞11 + 12 − 1 − 1+1 = 1 + 1 − 0 − 0 = 2 because → ∞ as → ∞. 89. (a) At the first step, only the interval 1 3 2 3 (length 1 3) is removed. At the second step, we remove the intervals 1 9 2 9 and 7 9 8 9, which have a total length of 2 · 1 32. At the third step, we remove 22 intervals, each of length 1 33. In general, at the nth step we remove 2−1 intervals, each of length 1 3, for a length of 2−1 · 1 3 = 1 3 2 3−1. Thus, the total length of all removed intervals is ∞ =1 1 3 2 3−1 = 1 −1233 = 1 geometric series with = 1 3 and = 2 3. Notice that at the th step, the leftmost interval that is removed is 1 3 2 3, so we never remove 0, and 0 is in the Cantor set. Also, the rightmost interval removed is 1 − 2 3 1 − 1 3, so 1 is never removed. Some other numbers in the Cantor set are 1 3, 2 3 , 1 9 , 2 9 , 7 9 , and 8 9. (b) The area removed at the first step is 1 9; at the second step, 8 · 1 92; at the third step, (8)2 · 1 93. In general, the area removed at the th step is (8)−1 1 9 = 1 9 8 9−1, so the total area of all removed squares is ∞ =1 1 9 89−1 = 1 −1989 = 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.2 SERIES ¤ 989 90. (a) 1 1 2 4 1 1 1000 2 2 3 1 4 1000 1 3 15 25 25 25 5005 5005 4 175 275 175 325 75025 25075 5 1625 2625 2125 2875 625375 375625 6 16875 26875 19375 30625 687813 313188 7 165625 265625 203125 296875 656594 344406 8 167188 267188 198438 301563 672203 328797 9 166406 266406 200781 299219 664398 336602 10 166797 266797 199609 300391 668301 332699 11 166602 266602 200195 299805 666350 334650 12 166699 266699 199902 300098 667325 333675 The limits seem to be 5 3, 8 3 , 2, 3, 667, and 334. Note that the limits appear to be “weighted” more toward 2. In general, we guess that the limit is 1 + 22 3 . (b) +1 − = 1 2( + −1) − = − 1 2( − −1) = − 1 2 1 2(−1 + −2) − −1 = − 1 2 − 1 2(−1 − −2) = · · · = − 1 2 −1 (2 − 1) Note that we have used the formula = 1 2(−1 + −2) a total of − 1 times in this calculation, once for each between 3 and + 1. Now we can write = 1 + (2 − 1) + (3 − 2) + · · · + (−1 − −2) + ( − −1) = 1 + −1 =1 (+1 − ) = 1 + −1 =1 − 1 2 −1 (2 − 1) and so lim →∞ = 1 + (2 − 1) ∞ =1 − 1 2 −1 = 1 + (2 − 1)1 − (1−12) = 1 + 2 3(2 − 1) = 1 + 2 3 2 . 91. (a) For ∞ =1 ( + 1)!, 1 = 1 1 · 2 = 1 2 , 2 = 1 2 + 2 1 · 2 · 3 = 5 6 , 3 = 5 6 + 3 1 · 2 · 3 · 4 = 23 24, 4 = 23 24 + 4 1 · 2 · 3 · 4 · 5 = 119 120 . The denominators are ( + 1)!, so a guess would be = ( + 1)! − 1 ( + 1)! . (b) For = 1, 1 = 1 2 = 2! − 1 2! , so the formula holds for = 1. Assume = ((+ 1)! + 1)! − 1. Then +1 = ( + 1)! − 1 ( + 1)! + + 1 ( + 2)! = ( + 1)! − 1 ( + 1)! + + 1 ( + 1)!( + 2) = ( + 2)! − ( + 2) + + 1 ( + 2)! = ( + 2)! − 1 ( + 2)! Thus, the formula is true for = + 1. So by induction, the guess is correct. (c) lim →∞ = lim →∞ ( + 1)! − 1 ( + 1)! = lim →∞ 1 − ( + 1)! 1 = 1 and so ∞=1 ( + 1)! = 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 990 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 92. Let 1 = radius of the large circle, 2 = radius of next circle, and so on. From the figure we have ∠ = 60◦ and cos 60◦ = 1 ||, so || = 21 and || = 22. Therefore, 21 = 1 + 2 + 22 ⇒ 1 = 32. In general, we have +1 = 1 3 , so the total area is = 12 + 322 + 332 + · · · = 12 + 3221 + 312 + 314 + 316 + · · · = 12 + 322 · 1 1 − 19 = 12 + 27 8 22 Since the sides of the triangle have length 1, || = 1 2 and tan 30◦ = 1 12. Thus, 1 = tan 30 2 ◦ = 2√13 ⇒ 2 = 6√13, so = 2√132 + 278 6√132 = 12 + 32 = 11 96 . The area of the triangle is √43, so the circles occupy about 831% of the area of the triangle. 11.3 The Integral Test and Estimates of Sums 1. The picture shows that 2 = 1 213 12 113 , 3 = 1 313 23 113 , and so on, so ∞=2 1 13 1∞ 113 . The integral converges by (7.8.2) with = 13 1, so the series converges. 2. From the first figure, we see that 16 () 5 =1 . From the second figure, we see that 6 =2 16 (). Thus, we have 6 =2 16 () 5 =1 . 3. The function () = −3 is continuous, positive, and decreasing on [1 ∞), so the Integral Test applies. 1∞ −3 = lim →∞ 1 −3 = lim →∞ −−22 1 = lim →∞ −212 + 1 2 = 12. Since this improper integral is convergent, the series ∞ =1 −3 is also convergent by the Integral Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.3 THE INTEGRAL TEST AND ESTIMATES OF SUMS ¤ 991 4. The function () = −03 is continuous, positive, and decreasing on [1 ∞), so the Integral Test applies. 1∞ −03 = lim →∞ 1 −03 = lim →∞ 0077 1 = lim →∞ 0077 − 017 = ∞. Since this improper integral is divergent, the series ∞ =1 −03 is also divergent by the Integral Test. 5. The function () = 2 5 − 1 is continuous, positive, and decreasing on [1 ∞), so the Integral Test applies. 1∞ 52− 1 = lim →∞ 1 52− 1 = lim →∞ 2 5 ln(5 − 1) 1 = lim →∞ 2 5 ln(5 − 1) − 2 5 ln 4 = ∞. Since this improper integral is divergent, the series ∞ =1 2 5 − 1 is also divergent by the Integral Test. 6. The function () = 1 (3 − 1)4 is continuous, positive, and decreasing on [1 ∞), so the Integral Test applies. 1∞ (3 −1 1)4 = lim →∞ 1(3 − 1)−4 = lim →∞ (−13)3(3 − 1)−3 1 = lim →∞ −9(31− 1)3 + 9 ·123 = 72 1 . Since this improper integral is convergent, the series ∞ =1 1 (3 − 1)4 is also convergent by the Integral Test. 7. The function () = 2 + 1 is continuous, positive, and decreasing on [1 ∞), so the Integral Test applies. 1∞ 2 + 1 = lim →∞ 1 2 + 1 = lim →∞ 1 2 ln(2 + 1) 1 = 1 2 lim →∞[ln(2 + 1) − ln 2] = ∞. Since this improper integral is divergent, the series ∞ =1 2 + 1 is also divergent by the Integral Test. 8. The function () = 2−3 is continuous, positive, and decreasing () on [1 ∞), so the Integral Test applies. 1∞ 2−3 = lim →∞ 1 2−3 = lim →∞−13−3 1 = −13 lim →∞ −3 − −1 = −130 − 1 = 31. Since this improper integral is convergent, the series ∞ =1 2−3 is also convergent by the Integral Test. (): 0() = 2−3(−32) + −3(2) = −3(−33 + 2) = (2 − 33) 3 0 for 1 9. ∞ =1 1 √2 is a -series with = √2 1, so it converges by (1). 10. ∞ =3 −09999 = ∞ =3 1 09999 is a -series with = 09999 ≤ 1, so it diverges by (1). The fact that the series begins with = 3 is irrelevant when determining convergence. 11. 1 + 1 8 + 1 27 + 1 64 + 1 125 + · · · = ∞ =1 1 3 . This is a -series with = 3 1, so it converges by (1). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 992 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 12. 1 5 + 1 7 + 1 9 + 1 11 + 1 13 + · · · = ∞ =1 1 2 + 3 . The function () = 1 2 + 3 is continuous, positive, and decreasing on [1 ∞), so the Integral Test applies. 1∞ 21+ 3 = lim →∞1 21+ 3 = lim →∞ 1 2 ln(2 + 3) 1 = lim →∞ 1 2 ln(2 + 3) − 1 2 ln 5 = ∞, so the series ∞ =1 1 2 + 3 diverges. 13. 1 3 + 1 7 + 1 11 + 1 15 + 1 19 + · · · = ∞ =1 1 4 − 1. The function () = 41− 1 is continuous, positive, and decreasing on [1 ∞), so the Integral Test applies. 1∞ 41− 1 = lim →∞1 41− 1 = lim →∞ 1 4 ln(4 − 1) 1 = lim →∞ 1 4 ln(4 − 1) − 1 4 ln 3 = ∞, so the series ∞ =1 1 4 − 1 diverges. 14. 1 + 1 2√2 + 1 3√3 + 1 4√4 + 1 5√5 + · · · = ∞ =1 1 √ = ∞ =1 1 32 . This is a -series with = 3 2 1, so it converges by (1). 15. ∞ =1 √ + 4 2 = ∞ =1√2 + 42 = ∞=1 312 + ∞=1 42 . ∞=1 312 is a convergent -series with = 3 2 1. ∞ =1 4 2 = 4 ∞ =1 1 2 is a constant multiple of a convergent -series with = 2 1, so it converges. The sum of two convergent series is convergent, so the original series is convergent. 16. The function () = √ 1 + 32 is continuous and positive on [1 ∞). 0() = (1 + 32) 1 2−12 − 12 3 212 (1 + 32)2 = 1 2 −12 + 1 2 − 3 2 (1 + 32)2 = 1 − 232 2√(1 + 32)2 0 for ≥ 1, so is decreasing on [1 ∞), and the Integral Test applies. 1∞ 1 +√32 = lim →∞1 1 +√32 = lim →∞ 2 3 ln(1 + 32) 1 withsubstitution = 1 + 32 = lim →∞ 2 3 ln(1 + 32) − 2 3 ln 2 = ∞, so the series ∞ =1 √ 1 + 32 diverges. 17. The function () = 1 2 + 4 is continuous, positive, and decreasing on [1 ∞), so we can apply the Integral Test. 1∞ 21+ 4 = lim →∞1 21+ 4 = lim →∞1 2 tan−1 2 1 = 12 lim →∞tan−12 − tan−11 2 = 1 2 2 − tan−11 2 Therefore, the series ∞ =1 1 2 + 4 converges. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.3 THE INTEGRAL TEST AND ESTIMATES OF SUMS ¤ 993 18. The function () = 1 2 + 2 + 2 is continuous, positive, and decreasing on [1 ∞), so the Integral Test applies. 1∞ 2 + 21 + 2 = lim →∞1 ( + 1) 1 2 + 1 = lim →∞arctan( + 1) 1 = lim →∞ [arctan( + 1) − arctan 2] = 2 − arctan 2, so the series ∞ =1 1 2 + 2 + 2 converges. 19. The function () = 3 4 + 4 is continuous and positive on [2 ∞), and is also decreasing since 0() = (4 + 4)(32) − 3(43) (4 + 4)2 = 122 − 6 (4 + 4)2 = 2(12 − 4) (4 + 4)2 0 for √4 12 ≈ 186, so we can use the Integral Test on [2 ∞). 2∞ 4+ 4 3 = lim →∞2 4+ 4 3 = lim →∞ 1 4 ln(4 + 4) 2 = lim →∞ 1 4 ln(4 + 4) − 1 4 ln 20 = ∞, so the series ∞ =2 3 4 + 4 diverges, and it follows that ∞ =1 3 4 + 4 diverges as well. 20. The function () = 3 − 4 2 − 2 = 2 + 1 − 2 [by partial fractions] is continuous, positive, and decreasing on [3 ∞) since it is the sum of two such functions, so we can apply the Integral Test. 3∞ 32 −− 4 = lim →∞3 2 + −1 2 = lim →∞2ln + ln( − 2) 3 = lim →∞[2 ln + ln( − 2) − 2ln3] = ∞. The integral is divergent, so the series ∞ =3 3 − 4 2 − is divergent. 21. () = 1 ln is continuous and positive on [2 ∞), and also decreasing since 0() = −1 + ln 2(ln)2 0 for 2, so we can use the Integral Test. 2∞ ln 1 = lim →∞[ln(ln)] 2 = lim →∞[ln(ln) − ln(ln 2)] = ∞, so the series ∞=2 ln 1 diverges. 22. The function () = ln 2 is continuous and positive on [2 ∞), and also decreasing since 0() = 2(1) − (ln)(2) (2)2 = − 2ln 4 = 1 − 2ln 3 0 for 12 ≈ 165, so we can use the Integral Test on [2 ∞). 2∞ ln2 = lim →∞2 ln2 = lim →∞−ln 2 + 2 12 = ln by parts with , = (12) = lim →∞−ln + ln 2 2 + −1 2 = lim H →∞−11 + ln 2 2 − 1 + 12 = ln 2 + 1 2 , so the series ∞ =2 ln 2 converges. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 994 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 23. The function () = − = is continuous and positive on [1 ∞), and also decreasing since 0() = · 1 − ()2 = (1 − ) ()2 = 1 − 0 for 1 [and (1) (2)], so we can use the Integral Test on [1 ∞). 1∞ − = lim →∞ 1 − = lim →∞ −− 1 + 1 − = by parts with , = − = lim →∞ −− + −1 + −− 1 = lim →∞ − + 1 − 1 + 1 H = lim →∞ −1 + 1 − 0 + 1 = 2 , so the series ∞ =1 − converges. 24. The function () = −2 = 2 is continuous and positive on [1 ∞), and also decreasing since 0() = 2 · 1 − 2 · 2 (2)2 = 1 − 22 2 0 for 1 2 ≈ 07, so we can use the Integral Test on [1 ∞). 1∞ −2 = lim →∞ 1 −2 = lim →∞ − 1 2 −2 1 = lim →∞ − 1 2 −2 + 1 2 −1 = 21, so the series ∞=1 −2 converges. 25. The function () = 1 2 + 3 = 1 2 − 1 + 1 + 1 [by partial fractions] is continuous, positive and decreasing on [1 ∞), so the Integral Test applies. 1∞ () = lim →∞ 112 − 1 + + 1 1 = lim →∞−1 − ln + ln( + 1) 1 = lim →∞−1 + ln + 1 + 1 − ln 2 = 0 + 0 + 1 − ln 2 The integral converges, so the series ∞ =1 1 2 + 3 converges. 26. The function () = 4 + 1 is positive, continuous, and decreasing on [1 ∞). [Note that 0() = 4 + 1 − 44 (4 + 1)2 = 1 − 34 (4 + 1)2 0 on [1 ∞).] Thus, we can apply the Integral Test. 1∞ 4 + 1 = lim →∞ 1 1 + ( 1 2(22))2 = lim →∞ 1 2 tan−1(2) 1 = 12 lim →∞[tan−1(2) − tan−1 1] = 122 − 4 = 8 so the series ∞ =1 4 + 1 converges. 27. The function () = cos √ is neither positive nor decreasing on [1 ∞), so the hypotheses of the Integral Test are not satisfied for the series ∞ =1 cos √ . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.3 THE INTEGRAL TEST AND ESTIMATES OF SUMS ¤ 995 28. The function () = cos2 1 + 2 is not decreasing on [1 ∞), so the hypotheses of the Integral Test are not satisfied for the series ∞ =1 cos2 1 + 2 . 29. We have already shown (in Exercise 21) that when = 1 the series ∞ =2 1 (ln) diverges, so assume that 6= 1. () = 1 (ln) is continuous and positive on [2 ∞), and 0() = −2(ln + ln )+1 0 if −, so that is eventually decreasing and we can use the Integral Test. 2∞ (ln1) = lim →∞(ln1−)1− 2 [for 6= 1] = lim →∞(ln1 −)1− − (ln 2) 1 −1− This limit exists whenever 1 − 0 ⇔ 1, so the series converges for 1. 30. () = 1 ln[ln(ln)] is positive and continuous on [3 ∞). For ≥ 0, clearly decreases on [3 ∞); and for 0, it can be verified that is ultimately decreasing. Thus, we can apply the Integral Test. = 3∞ ln[ln(ln )] = lim →∞3 [ln(ln ln)]− = lim →∞[ln(ln −+ 1 )]−+1 3 [for 6= 1] = lim →∞[ln(ln −+ 1 )]−+1 − [ln(ln 3)] − + 1 −+1 , which exists whenever − + 1 0 ⇔ 1. If = 1, then = lim →∞ ln(ln(ln)) 3 = ∞. Therefore, ∞ =3 1 ln[ln(ln)] converges for 1. 31. Clearly the series cannot converge if ≥ − 1 2, because then lim →∞ (1 + 2) 6= 0. So assume − 1 2. Then () = (1 + 2) is continuous, positive, and eventually decreasing on [1 ∞), and we can use the Integral Test. 1∞ (1 + 2) = lim →∞1 2 · (1 + + 1 2)+1 1 = 2(1+ 1) lim →∞[(1 + 2)+1 − 2+1]. This limit exists and is finite ⇔ + 1 0 ⇔ −1, so the series ∞ =1 (1 + 2) converges whenever −1. 32. If ≤ 0, lim →∞ ln = ∞ and the series diverges, so assume 0. () = ln is positive and continuous and 0() 0 for 1, so is eventually decreasing and we can use the Integral Test. Integration by parts gives 1∞ ln = lim →∞1− [(1(1−−)ln )2 − 1] 1 (for 6= 1) = (1 −1)2 lim →∞1− [(1 − )ln − 1] + 1, which exists whenever 1 − 0 ⇔ 1. Thus, ∞ =1 ln converges ⇔ 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 996 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 33. Since this is a -series with = , () is defined when 1. Unless specified otherwise, the domain of a function is the set of real numbers such that the expression for () makes sense and defines a real number. So, in the case of a series, it’s the set of real numbers such that the series is convergent. 34. (a) ∞ =2 1 2 = ∞ =1 1 2 − 1 21 [subtract 1] = 2 6 − 1 (b) ∞ =3 1 ( + 1)2 = ∞ =4 1 2 = ∞ =1 1 2 − 112 + 212 + 312 = 62 − 49 36 (c) ∞ =1 1 (2)2 = ∞ =1 1 42 = 1 4 ∞ =1 1 2 = 1 4 62 = 242 35. (a) ∞ =13 4 = ∞=1 814 = 81 ∞=1 14 = 81904 = 910 4 (b) ∞ =5 1 ( − 2)4 = 1 43 + 1 44 + 1 45 + · · · = ∞ =3 1 4 = 4 90 − 114 + 214 [subtract 1 and 2] = 904 − 17 16 36. (a) () = 14 is positive and continuous and 0() = −45 is negative for 0, and so the Integral Test applies. ∞ =1 1 4 ≈ 10 = 1 41 + 1 42 + 1 43 + · · · + 1 104 ≈ 1082037. 10 ≤ 10∞ 14 = lim →∞−313 10 = lim →∞−313 + 3 (10) 1 3 = 3000 1 , so the error is at most 00003. (b) 10 + 11∞ 14 ≤ ≤ 10 + 10∞ 14 ⇒ 10 + 3(11) 1 3 ≤ ≤ 10 + 3(10) 1 3 ⇒ 1082037 + 0000250 = 1082287 ≤ ≤ 1082037 + 0000333 = 1082370, so we get ≈ 108233 with error ≤ 000005. (c) The estimate in part (b) is ≈ 108233 with error ≤ 000005. The exact value given in Exercise 35 is 490 ≈ 1082323. The difference is less than 0.00001 (d) ≤ ∞ 14 = 313 . So 000001 ⇒ 313 10 15 ⇒ 33 105 ⇒ 3 (10)53 ≈ 322, that is, for 32. 37. (a) () = 1 2 is positive and continuous and 0() = −23 is negative for 0, and so the Integral Test applies. ∞ =1 1 2 ≈ 10 = 1 21 + 1 22 + 1 23 + · · · + 1 102 ≈ 1549768. 10 ≤ 10∞ 12 = lim →∞−1 10 = lim →∞−1 + 10 1 = 10 1 , so the error is at most 01. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.3 THE INTEGRAL TEST AND ESTIMATES OF SUMS ¤ 997 (b) 10 + 11∞ 12 ≤ ≤ 10 + 10∞ 12 ⇒ 10 + 11 1 ≤ ≤ 10 + 10 1 ⇒ 1549768 + 0090909 = 1640677 ≤ ≤ 1549768 + 01 = 1649768, so we get ≈ 164522 (the average of 1640677 and 1649768) with error ≤ 0005 (the maximum of 1649768 − 164522 and 164522 − 1640677, rounded up). (c) The estimate in part (b) is ≈ 164522 with error ≤ 0005. The exact value given in Exercise 34 is 26 ≈ 1644934. The difference is less than 00003. (d) ≤ ∞ 12 = 1 . So 0001 if 1 1000 1 ⇔ 1000. 38. () = −2 is continuous, positive, and decreasing on [1 ∞), so the Integral Test applies. Using (2), ≤ ∞ −2 = lim →∞− 1 2 −2 + 1 2 −2 =using parts with , = −2 = lim →∞2−2 + 22 − 412 + 412 = 0 + H 22 − 0 + 412 = 24+ 1 2 To be correct to four decimal places, we want 2 + 1 42 ≤ 10 55 . This inequality is true for = 6. 6 = 6 =1 2 = 1 2 + 2 4 + 3 6 + 4 8 + 5 10 + 6 12 ≈ 01810. 39. () = 1(2 + 1)6 is continuous, positive, and decreasing on [1 ∞), so the Integral Test applies. Using (2), ≤ ∞(2 + 1)−6 = lim →∞10(2− 1+ 1)5 = 10(21+ 1)5 . To be correct to five decimal places, we want 1 10(2 + 1)5 ≤ 10 56 ⇔ (2 + 1)5 ≥ 20,000 ⇔ ≥ 1 2√5 20,000 − 1 ≈ 312, so use = 4. 4 = 4 =1 1 (2 + 1)6 = 1 63 + 1 65 + 1 67 + 1 69 ≈ 0001 446 ≈ 000145. 40. () = 1 (ln)2 is positive and continuous and 0() = −ln2(ln + 2 )3 is negative for 1, so the Integral Test applies. Using (2), we need 001 ∞ (ln )2 = lim →∞ln −1 = ln1. This is true for 100, so we would have to add this many terms to find the sum of the series ∞ =2 1 (ln)2 to within 001, which would be problematic because 100 ≈ 27 × 1043. 41. ∞ =1 −1001 = ∞ =1 1 1001 is a convergent -series with = 1001 1. Using (2), we get ≤ ∞ −1001 = lim →∞−−00001 001 = −1000 lim →∞01001 = −1000−01001 = 1000 0001 . We want °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 998 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 0000000005 ⇔ 1000 0001 5 × 10−9 ⇔ 0001 5 ×1000 10−9 ⇔ 2 × 10111000 = 21000 × 1011,000 ≈ 107 × 10301 × 1011,000 = 107 × 1011,301. 42. (a) () = ln2 is continuous and positive for 1, and since 0() = 2ln(1 3− ln) 0 for , we can apply the Integral Test. Using a CAS, we get 1∞ ln2 = 2, so the series ∞=1 ln2 also converges. (b) Since the Integral Test applies, the error in ≈ is ≤ ∞ ln2 = (ln)2 + 2 ln + 2. (c) By graphing the functions 1 = (ln)2 + 2 ln + 2 and 2 = 005, we see that 1 2 for ≥ 1373. (d) Using the CAS to sum the first 1373 terms, we get 1373 ≈ 194. 43. (a) From the figure, 2 + 3 + · · · + ≤ 1 (), so with () = 1 , 1 2 + 1 3 + 1 4 + · · · + 1 ≤ 1 1 = ln. Thus, = 1 + 1 2 + 1 3 + 1 4 + · · · + 1 ≤ 1 + ln. (b) By part (a), 106 ≤ 1 + ln 106 ≈ 1482 15 and 109 ≤ 1 + ln 109 ≈ 2172 22. 44. (a) The sum of the areas of the rectangles in the graph to the right is 1 + 1 2 + 1 3 + · · · + 1 . Now 1+1 is less than this sum because the rectangles extend above the curve = 1, so 1+1 1 = ln( + 1) 1 + 1 2 + 1 3 + · · · + 1 , and since ln ln( + 1), 0 1 + 1 2 + 1 3 + · · · + 1 − ln = . (b) The area under () = 1 between = and = + 1 is +1 = ln( + 1) − ln, and this is clearly greater than the area of the inscribed rectangle in the figure to the right which is + 1 1 , so − +1 = [ln( + 1) − ln] − 1 + 1 0, and so +1, so {} is a decreasing sequence. (c) We have shown that {} is decreasing and that 0 for all . Thus, 0 ≤ 1 = 1, so {} is a bounded monotonic sequence, and hence converges by the Monotonic Sequence Theorem. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.4 THE COMPARISON TESTS ¤ 999 45. ln = ln ln = ln ln = ln = 1 − ln . This is a -series, which converges for all such that −ln 1 ⇔ ln −1 ⇔ −1 ⇔ 1 [with 0]. 46. For the series ∞ =1 − + 1 1 , = =1 − + 1 1 = 1 − 1 2 + 2 − 1 3 + 3 − 14 + · · · + − + 1 1 = 1 + − 1 2 + − 1 3 + − 1 4 + · · · + − 1 − 1 + 1 = + ( − 1)12 + 13 + 1 4 + · · · + 1 − + 1 1 Thus, ∞ =1 − + 1 1 = lim →∞ = lim →∞ + ( − 1) =2 1 − + 1 1 . Since a constant multiple of a divergent series is divergent, the last limit exists only if − 1 = 0, so the original series converges only if = 1. 11.4 The Comparison Tests 1. (a) We cannot say anything about . If for all and is convergent, then could be convergent or divergent. (See the note after Example 2.) (b) If for all , then is convergent. [This is part (i) of the Comparison Test.] 2. (a) If for all , then is divergent. [This is part (ii) of the Comparison Test.] (b) We cannot say anything about . If for all and is divergent, then could be convergent or divergent. 3. 1 3 + 8 1 3 for all ≥ 1, so ∞ =1 1 3 + 8 converges by comparison with ∞ =1 1 3 , which converges because it is a -series with = 3 1. 4. √1− 1 √1 for all ≥ 2, so ∞ =2 1 √ − 1 diverges by comparison with ∞ =2 1 √ , which diverges because it is a -series with = 1 2 ≤ 1. 5. + 1 √ √ = 1 √ for all ≥ 1, so ∞ =1 + 1 √ diverges by comparison with ∞ =1 1 √ , which diverges because it is a p-series with = 1 2 ≤ 1. 6. − 1 3 + 1 3 + 1 3 = 1 2 for all ≥ 1, so ∞ =1 − 1 3 + 1 converges by comparison with ∞ =1 1 2 , which converges because it is a -series with = 2 1. 7. 9 3 + 10 9 10 = 10 9 for all ≥ 1. ∞=1 10 9 is a convergent geometric series || = 10 9 1, so ∞=1 3 + 10 9 converges by the Comparison Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1000 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 8. 6 5 − 1 6 5 = 65 for all ≥ 1. ∞=1 6 5 is a divergent geometric series || = 6 5 1, so ∞=1 56− 1 diverges by the Comparison Test. 9. ln 1 for all k ≥ 3 [since ln 1 for ≥ 3], so ∞ =3 ln diverges by comparison with ∞ =3 1 , which diverges because it is a -series with = 1 ≤ 1 (the harmonic series). Thus, ∞ =1 ln diverges since a finite number of terms doesn’t affect the convergence or divergence of a series. 10. sin2 1 + 3 ≤ 1 +3 3 = 12 for all ≥ 1, so ∞=1 1 + sin2 3 converges by comparison with ∞=1 12 , which converges because it is a -series with = 2 1. 11. √3 √3 + 4 + 3 √3 √3 = 13 32 = 1 76 for all ≥ 1, so ∞ =1 √3 √3 + 4 + 3 converges by comparison with ∞ =1 1 76 , which converges because it is a -series with = 7 6 1. 12. (2 − 1)(2 − 1) ( + 1)(2 + 4)2 2(2) (2)2 = 23 5 = 2 2 for all ≥ 1, so ∞ =1 (2 − 1)(2 − 1) ( + 1)(2 + 4)2 converges by comparison with 2 ∞ =1 1 2 , which converges because it is a constant multiple of a -series with = 2 1. 13. 1 + cos 2 for all ≥ 1. ∞ =1 2 is a convergent geometric series (|| = 1 1), so ∞ =1 1 + cos converges by the Comparison Test. 14. 1 √3 34 + 1 1 √3 34 1 √3 4 = 1 43 for all ≥ 1, so ∞ =1 1 √3 34 + 1 converges by comparison with ∞ =1 1 43 , which converges because it is a -series with = 4 3 1. 15. 4+1 3 − 2 4 · 4 3 = 434 for all ≥ 1. ∞=1 443 = 4 ∞=14 3 is a divergent geometric series || = 4 3 1, so ∞ =1 4+1 3 − 2 diverges by the Comparison Test. 16. 1 ≤ 1 2 for all ≥ 1, so ∞ =1 1 converges by comparison with ∞ =1 1 2 , which converges because it is a -series with = 2 1. 17. Use the Limit Comparison Test with = √21+ 1 and = 1 : lim →∞ = lim →∞ √2+ 1 = lim →∞ 1 + (1 1 2) = 1 0. Since the harmonic series ∞=1 1 diverges, so does ∞ =1 1 √2 + 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.4 THE COMPARISON TESTS ¤ 1001 18. Use the Limit Comparison Test with = √2+ 2 and = √1: lim →∞ = lim →∞ √2√+ 2 = lim →∞ 1 + 22√ = 2 0. Since ∞=1 √1 is a divergent -series [ = 1 2 ≤ 1], the series ∞ =1 2 √ + 2 is also divergent. 19. Use the Limit Comparison Test with = + 1 3 + and = 12 : lim →∞ = lim →∞ ( (+ 1) 2 + 1) 2 = lim →∞ 22 ++ 1 = lim →∞ 1 + 1 1 + 1 2 = 1 0. Since ∞=1 12 is a convergent -series [ = 2 1], the series ∞ =1 + 1 3 + also converges. 20. Use the Limit Comparison Test with = 2 + + 1 4 + 2 and = 12 : lim →∞ = lim →∞ (2 2+(2+ 1) + 1)2 = lim →∞ 2+2 + 1 + 1 = lim →∞ 1 + 1 1 + 1 + 1 22 = 1 0. Since ∞=1 12 is a convergent -series [ = 2 1], the series ∞ =1 2 + + 1 4 + 2 also converges. 21. Use the Limit Comparison Test with = √1 + 2 + and = √1: lim →∞ = lim →∞ √1 + √ 2 + = lim →∞ √2 + √2 (2 + ) = lim →∞ 1 + 1 2 + 1 = 1 0. Since ∞ =1 1 √ is a divergent -series [ = 1 2 ≤ 1], the series ∞ =1 √1 + 2 + also diverges. 22. Use the Limit Comparison Test with = + 2 ( + 1)3 and = 12 : lim →∞ = lim →∞ (2(+ 1) + 2) 3 = lim →∞ 1 + 1 + 123 = 1 0. Since ∞=3 12 is a convergent (partial) -series [ = 2 1], the series ∞ =3 + 2 ( + 1)3 also converges. 23. Use the Limit Comparison Test with = 5 + 2 (1 + 2)2 and = 13 : lim →∞ = lim →∞ (1 + 3(5 + 2 2)2) = lim →∞ 5(1 + 3 + 2 2)24 · 11( 24)2 = lim →∞ 152 + 2 + 12 = 2 0. Since ∞=1 13 is a convergent -series [ = 3 1], the series ∞ =1 5 + 2 (1 + 2)2 also converges. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1002 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 24. + 3 + 2 3 + 2 3 2 + 2 = 3 2 · 2 = 1 2 23, so the series ∞ =1 + 3 + 2 diverges by comparison with 1 2 ∞ =1 3 2, which is a constant multiple of a divergent geometric series [|| = 3 2 1]. Or: Use the Limit Comparison Test with = + 3 + 2 and = 3 2. 25. + 1 + 1 ≥ + 1 + = + 1 ( + 1) = 1 for ≥ 1, so the series ∞ =1 + 1 + 1 diverges by comparison with the divergent harmonic series ∞ =1 1 . Or: Use the Limit Comparison Test with = + 1 + 1 and = 1 . 26. If = 1 √2 − 1 and = 12 , then lim →∞ = lim →∞ √22− 1 = lim →∞ √2 − 1 = lim →∞ 1 −112 = 11 = 1 0, so ∞=2 √12 − 1 converges by the Limit Comparison Test with the convergent series ∞ =2 1 2. 27. Use the Limit Comparison Test with = 1 + 1 2 − and = −: lim →∞ = lim →∞1 + 1 2 = 1 0. Since ∞ =1 − = ∞ =1 1 is a convergent geometric series || = 1 1, the series ∞ =1 1 + 1 2 − also converges. 28. 1 1 for all ≥ 1, so ∞ =1 1 diverges by comparison with the harmonic series ∞ =1 1 . 29. Clearly ! = ( − 1)( − 2)· · ·(3)(2) ≥ 2 · 2 · 2 · · · · · 2 · 2 = 2−1, so 1 ! ≤ 21−1 . ∞ =1 1 2−1 is a convergent geometric series || = 1 2 1, so ∞ =1 1 ! converges by the Comparison Test. 30. ! = 1 · 2 · 3 · · · · · ( − 1) · · · · · · · · ≤ 1 · 2 · 1 · 1 · · · · · 1 for ≥ 2, so since ∞ =1 2 2 converges [ = 2 1], ∞ =1 ! converges also by the Comparison Test. 31. Use the Limit Comparison Test with = sin1 and = 1 . Then and are series with positive terms and lim →∞ = lim →∞ sin(1 1) = lim →0 sin = 1 0. Since ∞=1 is the divergent harmonic series, ∞ =1 sin (1) also diverges. [Note that we could also use l’Hospital’s Rule to evaluate the limit: lim →∞ sin(1) 1 H = lim →∞ cos(1) · −12 −12 = lim →∞cos 1 = cos 0 = 1.] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.4 THE COMPARISON TESTS ¤ 1003 32. Use the Limit Comparison Test with = 1 1+1 and = 1 . lim →∞ = lim →∞ 1+1 = lim →∞ 11 = 1 since lim →∞1 = 1 by l’Hospital’s Rule, so ∞ =1 1 diverges [harmonic series] ⇒ ∞ =1 1 1+1 diverges. 33. 10 =1 1 5 + 5 = 1 5 + 15 + 1 5 + 25 + 1 5 + 35 + · · · + 1 5 + 105 ≈ 019926. Now 5 +15 15 , so the error is 10 ≤ 10 ≤ 10∞ 15 = lim →∞10 −5 = lim →∞4−14 10 = lim →∞4−14 + 40,1000 = 40,1000 = 0000 025. 34. 10 =1 1 4 = 11 14 + 12 24 + 13 34 + · · · + 110 104 ≈ 284748. Now 1 4 ≤ 4 for ≥ 1, so the error is 10 ≤ 10 ≤ 10∞ 4 = lim →∞10 −4 = lim →∞3−3 10 = lim →∞3−3 + 3000 = 3000 ≈ 0000 906. 35. 10 =1 5− cos2 = cos2 1 5 + cos2 2 52 + cos2 3 53 + · · · + cos2 10 510 ≈ 007393. Now cos 52 ≤ 51 , so the error is 10 ≤ 10 ≤ 10∞ 51 = lim →∞10 5− = lim →∞−5ln 5 − 10 = lim →∞−ln 5 5− + 5ln 5 −10 = 5101ln 5 64 × 10−8. 36. 10 =1 1 3 + 4 = 1 31 + 41 + 1 32 + 42 + 1 33 + 43 + · · · + 1 310 + 410 ≈ 019788. Now 3 + 4 1 3 + 3 1 = 2 ·13 , so the error is 10 ≤ 10 ≤ 10∞ 2 ·13 = lim →∞10 1 2 · 3− = lim →∞−12 3ln 3 − 10 = lim →∞−12 ln 3 3− + 12 3ln 3 −10 = 1 2 · 310 ln 3 77 × 10−6 37. Since 10 ≤ 9 10 for each , and since ∞ =1 9 10 is a convergent geometric series || = 10 1 1, 0123 = ∞ =1 10 will always converge by the Comparison Test. 38. Clearly, if 0 then the series diverges, since lim →∞ 1 ln = ∞. If 0 ≤ ≤ 1, then ln ≤ ln ⇒ 1 ln ≥ ln 1 and ∞ =2 1 ln diverges (Exercise 11.3.21), so ∞ =2 1 ln diverges. If 1, use the Limit Comparison Test with = 1 ln and = 1 . ∞ =2 converges, and lim →∞ = lim →∞ ln1 = 0, so ∞=2 1ln also converges. (Or use the Comparison Test, since ln for .) In summary, the series converges if and only if 1. 39. Since converges, lim →∞ = 0, so there exists such that | − 0| 1 for all ⇒ 0 ≤ 1 for all ⇒ 0 ≤ 2 ≤ . Since converges, so does 2 by the Comparison Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1004 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 40. (a) Since lim →∞ () = 0, there is a number 0 such that | − 0| 1 for all , and so since and are positive. Thus, since converges, so does by the Comparison Test. (b) (i) If = ln 3 and = 12 , then lim →∞ = lim →∞ ln = lim →∞ ln = lim H →∞ 1 1 = 0, so ∞=1 ln3 converges by part (a). (ii) If = √ln and = 1 , then lim →∞ = lim →∞ ln √ = lim →∞ ln √ = lim H →∞ 1(2 1 √) = lim →∞ √2 = 0. Now is a convergent geometric series with ratio = 1 [|| 1], so converges by part (a). 41. (a) Since lim →∞ = ∞, there is an integer such that 1 whenever . (Take = 1 in Definition 11.1.5.) Then whenever and since is divergent, is also divergent by the Comparison Test. (b) (i) If = 1 ln and = 1 for ≥ 2, then lim →∞ = lim →∞ ln = lim →∞ ln = lim H →∞ 1 1 = lim →∞ = ∞, so by part (a), ∞ =2 1 ln is divergent. (ii) If = ln and = 1 , then ∞ =1 is the divergent harmonic series and lim →∞ = lim →∞ln = lim →∞ln = ∞, so ∞ =1 diverges by part (a). 42. Let = 1 2 and = 1 . Then lim →∞ = lim →∞ 1 = 0, but diverges while converges. 43. lim →∞ = lim →∞ 1 , so we apply the Limit Comparison Test with = 1 . Since lim →∞ 0 we know that either both series converge or both series diverge, and we also know that ∞ =1 1 diverges [-series with = 1]. Therefore, must be divergent. 44. First we observe that, by l’Hospital’s Rule, lim →0 ln(1 + ) = lim →0 1 1 + = 1. Also, if converges, then lim →∞ = 0 by Theorem 11.2.6. Therefore, lim →∞ ln(1 + ) = lim →0 ln(1 + ) = 1 0. We are given that is convergent and 0. Thus, ln(1 + ) is convergent by the Limit Comparison Test. 45. Yes. Since is a convergent series with positive terms, lim →∞ = 0 by Theorem 11.2.6, and = sin() is a series with positive terms (for large enough ). We have lim →∞ = lim →∞ sin() = 1 0 by Theorem 3.3.2. Thus, is also convergent by the Limit Comparison Test. 46. Yes. Since converges, its terms approach 0 as → ∞, so for some integer , ≤ 1 for all ≥ . But then ∞ =1 = =1 −1 + ∞ = ≤ =1 −1 + ∞ = . The first term is a finite sum, and the second term converges since ∞ =1 converges. So converges by the Comparison Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.5 ALTERNATING SERIES ¤ 1005 11.5 Alternating Series 1. (a) An alternating series is a series whose terms are alternately positive and negative. (b) An alternating series ∞ =1 = ∞ =1 (−1)−1, where = ||, converges if 0 +1 ≤ for all and lim →∞ = 0. (This is the Alternating Series Test.) (c) The error involved in using the partial sum as an approximation to the total sum is the remainder = − and the size of the error is smaller than +1; that is, || ≤ +1. (This is the Alternating Series Estimation Theorem.) 2. 2 3 − 2 5 + 2 7 − 2 9 + 2 11 − · · · = ∞ =1 (−1)+1 2 2 + 1 . Now = 2 2 + 1 0, {} is decreasing, and lim →∞ = 0, so the series converges by the Alternating Series Test. 3. −2 5 + 4 6 − 6 7 + 8 8 − 10 9 + · · · = ∞ =1 (−1) 2 + 4. Now lim →∞ = lim →∞ 2+ 4 = lim →∞ 1 + 4 2 = 2 1 6= 0. Since lim →∞ 6= 0 (in fact the limit does not exist), the series diverges by the Test for Divergence. 4. 1 ln 3 − 1 ln 4 + 1 ln 5 − 1 ln 6 + 1 ln 7 − · · · = ∞ =1 (−1)+1 ln( + 2). Now = ln(1+ 2) 0, {} is decreasing, and lim →∞ = 0, so the series converges by the Alternating Series Test. 5. ∞ =1 = ∞ =1 (−1)−1 3 + 5 = ∞ =1 (−1)−1. Now = 1 3 + 5 0, {} is decreasing, and lim →∞ = 0, so the series converges by the Alternating Series Test. 6. ∞ =0 = ∞ =0 (−1)+1 √ + 1 = ∞ =0 (−1)+1. Now = √1+ 1 0, {} is decreasing, and lim →∞ = 0, so the series converges by the Alternating Series Test. 7. ∞ =1 = ∞ =1 (−1) 3 − 1 2 + 1 = ∞ =1 (−1). Now lim →∞ = lim →∞ 3 − 1 2 + 1 = 3 2 6= 0. Since lim →∞ 6= 0 (in fact the limit does not exist), the series diverges by the Test for Divergence. 8. ∞ =1 = ∞ =1 (−1) 2 2 + + 1 = ∞ =1 (−1). Now lim →∞ = lim →∞ 2 2 + + 1 = lim →∞ 1 + 11+ 12 = 1 6= 0. Since lim →∞ 6= 0, the series diverges by the Test for Divergence. 9. ∞ =1 = ∞ =1 (−1)− = ∞ =1 (−1). Now = 1 0, {} is decreasing, and lim →∞ = 0, so the series converges by the Alternating Series Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1006 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 10. = √ 2 + 3 0 for ≥ 1. {} is decreasing for ≥ 2 since 2√+ 3 0 = (2 + 3)(2 1 2 −+ 3) 122− 12(2) = 1 2 −12(2 [(2 + 3) + 3) 2 − 4] = 2√3(2 −2+ 3) 2 0 for 3 2. Also, lim →∞ = lim →∞ √√ (2 + 3)√ = lim →∞ 2√ + 3 1 √ = 0. Thus, the series ∞=1(−1) 2√+ 3 converges by the Alternating Series Test. 11. = 2 3 + 4 0 for ≥ 1. {} is decreasing for ≥ 2 since 3+ 4 2 0 = (3 + 4)(2 (3+ 4) ) − 22(32) = (2(33+ 8 + 4) −233) = ((83 −+ 4) 32) 0 for 2. Also, lim →∞ = lim →∞ 1 1 + 43 = 0. Thus, the series ∞ =1 (−1)+1 2 3 + 4 converges by the Alternating Series Test. 12. = − = 0 for ≥ 1. {} is decreasing for ≥ 1 since (−)0 = (−−) + − = −(1 − ) 0 for 1. Also, lim →∞ = 0 since lim →∞ H = lim →∞ 1 = 0. Thus, the series ∞ =1 (−1)+1− converges by the Alternating Series Test. 13. lim →∞ = lim →∞ 2 = 0 = 1, so lim →∞ (−1)−12 does not exist. Thus, the series ∞ =1 (−1)−12 diverges by the Test for Divergence. 14. lim →∞ = lim →∞ arctan = 2 , so lim →∞ (−1)−1 arctan does not exist. Thus, the series ∞ =1 (−1)−1 arctan diverges by the Test for Divergence. 15. = sin + 1 2 1 + √ = (−1) 1 + √. Now = 1 +1√ 0 for ≥ 0, {} is decreasing, and lim →∞ = 0, so the series ∞ =0 sin + 1 2 1 + √ converges by the Alternating Series Test. 16. = cos 2 = (−1) 2 = (−1). {} is decreasing for ≥ 2 since (2−)0 = (−2− ln 2) + 2− = 2−(1 − ln 2) 0 for 1 ln 2 [≈14]. Also, lim →∞ = 0 since lim →∞ 2 H = lim →∞ 1 2 ln 2 = 0. Thus, the series ∞ =1 cos 2 converges by the Alternating Series Test. 17. ∞ =1 (−1) sin. = sin 0 for ≥ 2 and sin ≥ sin + 1 , and lim →∞ sin = sin 0 = 0, so the series converges by the Alternating Series Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.5 ALTERNATING SERIES ¤ 1007 18. ∞ =1 (−1) cos. lim →∞cos = cos(0) = 1, so lim →∞(−1) cos does not exist and the series diverges by the Test for Divergence. 19. ! = · · · · · · 1 · 2 · · · · · ≥ ⇒ lim →∞ ! = ∞ ⇒ lim →∞ (−1) ! does not exist. So the series ∞ =1 (−1) ! diverges by the Test for Divergence. 20. = √ + 1 − √ 1 · √ + 1 + √ √ + 1 + √ = ( + 1) − √ + 1 + √ = 1 √ + 1 + √ 0 for ≥ 1. {} is decreasing and lim →∞ = 0, so the series ∞ =1 (−1)√ + 1 − √ converges by the Alternating Series Test. 21. The graph gives us an estimate for the sum of the series ∞ =1 (−08) ! of −055. 8 = (08) 8! ≈ 0000 004, so ∞ =1 (−08) ! ≈ 7 = 7 =1 (−08) ! ≈ −08 + 032 − 00853 + 001706 − 0002 731 + 0000 364 − 0000 042 ≈ −05507 Adding 8 to 7 does not change the fourth decimal place of 7, so the sum of the series, correct to four decimal places, is −05507. 22. The graph gives us an estimate for the sum of the series ∞ =1 (−1)−1 8 of 01. 6 = 6 86 ≈ 0000 023, so ∞ =1 (−1)−1 8 ≈ 5 = 5 =1 (−1)−1 8 ≈ 0125 − 003125 + 0005 859 − 0000 977 + 0000 153 ≈ 00988 Adding 6 to 5 does not change the fourth decimal place of 5, so the sum of the series, correct to four decimal places, is 00988. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1008 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 23. The series ∞ =1 (−1)+1 6 satisfies (i) of the Alternating Series Test because ( + 1) 1 6 16 and (ii) lim →∞ 16 = 0, so the series is convergent. Now 5 = 1 56 = 0000064 000005 and 6 = 616 ≈ 000002 000005, so by the Alternating Series Estimation Theorem, = 5. (That is, since the 6th term is less than the desired error, we need to add the first 5 terms to get the sum to the desired accuracy.) 24. The series ∞ =1 (− 1 3) = ∞ =1 (−1) 1 3 satisfies (i) of the Alternating Series Test because 1 ( + 1)3+1 1 3 and (ii) lim →∞ 1 3 = 0, so the series is convergent. Now 5 = 1 5 · 35 ≈ 00008 00005 and 6 = 6 ·136 ≈ 00002 00005, so by the Alternating Series Estimation Theorem, = 5. (That is, since the 6th term is less than the desired error, we need to add the first 5 terms to get the sum to the desired accuracy.) 25. The series ∞ =1 (−1)−1 22 satisfies (i) of the Alternating Series Test because ( + 1) 122+1 212 and (ii) lim →∞ 212 = 0, so the series is convergent. Now 5 = 1 5225 = 000125 00005 and 6 = 62126 ≈ 00004 00005, so by the Alternating Series Estimation Theorem, = 5. (That is, since the 6th term is less than the desired error, we need to add the first 5 terms to get the sum to the desired accuracy.) 26. The series ∞ =1 −1 = ∞=1(−1) 1 satisfies (i) of the Alternating Series Test because ( + 1) 1 +1 1 and (ii) lim →∞ 1 = 0, so the series is convergent. Now 5 = 1 55 = 000032 000005 and 6 = 616 ≈ 000002 000005, so by the Alternating Series Estimation Theorem, = 5. (That is, since the 6th term is less than the desired error, we need to add the first 5 terms to get the sum to the desired accuracy.) 27. 4 = 1 8! = 1 40,320 ≈ 0000 025, so ∞ =1 (−1) (2)! ≈ 3 = 3 =1 (−1) (2)! = − 1 2 + 1 24 − 1 720 ≈ −0459 722 Adding 4 to 3 does not change the fourth decimal place of 3, so by the Alternating Series Estimation Theorem, the sum of the series, correct to four decimal places, is −04597. 28. ∞ =1 (−1)+1 6 ≈ 9 = 1 61 − 1 62 + 1 63 − 1 64 + 1 65 − 1 66 + 1 67 − 1 68 + 1 69 ≈ 0985 552. Subtracting 10 = 1106 from 9 does not change the fourth decimal place of 9, so by the Alternating Series Estimation Theorem, the sum of the series, correct to four decimal places, is 09856. 29. ∞ =1 (−1)−2 ≈ 5 = − 1 2 + 2 4 − 3 6 + 4 8 − 5 10 ≈ −0105 025. Adding 6 = 612 ≈ 0000 037 to 5 does not change the fourth decimal place of 5, so by the Alternating Series Estimation Theorem, the sum of the series, correct to four decimal places, is −01050. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.5 ALTERNATING SERIES ¤ 1009 30. ∞ =1 (−1)−1 4 ≈ 6 = 1 4 − 1 2 · 42 + 1 3 · 43 − 1 4 · 44 + 1 5 · 45 − 1 6 · 46 ≈ 0223136. Adding 7 = 7 ·147 ≈ 0000 0087 to 6 does not change the fourth decimal place of 6, so by the Alternating Series Estimation Theorem, the sum of the series, correct to four decimal places, is 02231. 31. ∞ =1 (−1)−1 = 1 − 1 2 + 1 3 − 1 4 + · · · + 1 49 − 1 50 + 1 51 − 1 52 + · · · . The 50th partial sum of this series is an underestimate, since ∞ =1 (−1)−1 = 50 +51 1 − 52 1 +53 1 − 54 1 + · · · , and the terms in parentheses are all positive. The result can be seen geometrically in Figure 1. 32. If 0, 1 ( + 1) ≤ 1 ({1} is decreasing) and lim →∞ 1 = 0, so the series converges by the Alternating Series Test. If ≤ 0, lim →∞ (−1)−1 does not exist, so the series diverges by the Test for Divergence. Thus, ∞ =1 (−1)−1 converges ⇔ 0. 33. Clearly = 1 + is decreasing and eventually positive and lim →∞ = 0 for any . So the series ∞ =1 (−1) + converges (by the Alternating Series Test) for any for which every is defined, that is, + 6= 0 for ≥ 1, or is not a negative integer. 34. Let () = (ln) . Then 0() = (ln)−1 ( − ln) 2 0 if so is eventually decreasing for every . Clearly lim →∞ (ln) = 0 if ≤ 0, and if 0 we can apply l’Hospital’s Rule [[ + 1]] times to get a limit of 0 as well. So the series ∞ =2 (−1)−1 (ln) converges for all (by the Alternating Series Test). 35. 2 = 1(2)2 clearly converges (by comparison with the -series for = 2). So suppose that (−1)−1 converges. Then by Theorem 11.2.8(ii), so does (−1)−1 + = 21 + 1 3 + 1 5 + · · · = 2 21− 1. But this diverges by comparison with the harmonic series, a contradiction. Therefore, (−1)−1 must diverge. The Alternating Series Test does not apply since {} is not decreasing. 36. (a) We will prove this by induction. Let () be the proposition that 2 = 2 − . (1) is the statement 2 = 2 − 1, which is true since 1 − 1 2 = 1 + 1 2 − 1. So suppose that () is true. We will show that ( + 1) must be true as a consequence. 2+2 − +1 = 2 + 21+ 1 + 21+ 2 − + + 1 1 = (2 − ) + 21+ 1 − 21+ 2 = 2 + 1 2 + 1 − 1 2 + 2 = 2+2 which is ( + 1), and proves that 2 = 2 − for all . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1010 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES (b) We know that 2 − ln(2) → and − ln → as → ∞. So 2 = 2 − = [2 − ln(2)] − ( − ln) + [ln(2) − ln], and lim →∞ 2 = − + lim →∞ [ln(2) − ln] = lim →∞ (ln 2 + ln − ln) = ln 2. 11.6 Absolute Convergence and the Ratio and Root Tests 1. (a) Since lim →∞ +1 = 8 1, part (b) of the Ratio Test tells us that the series is divergent. (b) Since lim →∞ +1 = 08 1, part (a) of the Ratio Test tells us that the series is absolutely convergent (and therefore convergent). (c) Since lim →∞ +1 = 1, the Ratio Test fails and the series might converge or it might diverge. 2. = √1 0 for ≥ 1, {} is decreasing for ≥ 1, and lim →∞ = 0, so ∞=1 (−√1)−1 converges by the Alternating Series Test. To determine absolute convergence, note that ∞ =1 1 √ diverges because it is a -series with = 1 2 ≤ 1. Thus, the series ∞ =1 (−1)−1 √ is conditionally convergent. 3. = 1 5 + 1 0 for ≥ 0, {} is decreasing for ≥ 0, and lim →∞ = 0, so ∞ =0 (−1) 5 + 1 converges by the Alternating Series Test. To determine absolute convergence, choose = 1 to get lim →∞ = lim →∞ 1(51+ 1) = lim →∞ 5+ 1 = 5 0, so ∞=1 51+ 1 diverges by the Limit Comparison Test with the harmonic series. Thus, the series ∞ =0 (−1) 5 + 1 is conditionally convergent. 4. 0 1 3 + 1 1 3 for ≥ 1 and ∞ =1 1 3 is a convergent -series ( = 3 1), so ∞ =1 1 3 + 1 converges by comparison and the series ∞ =1 (−1) 3 + 1 is absolutely convergent. 5. 0 sin 2 1 2 for ≥ 1 and ∞ =1 1 2 is a convergent geometric series ( = 1 2 1), so ∞ =1 sin 2 converges by comparison and the series ∞ =1 sin 2 is absolutely convergent. 6. = 2 + 4 0 for ≥ 1, {} is decreasing for ≥ 2, and lim →∞ = 0, so ∞ =1 (−1)−1 2 + 4 converges by the Alternating Series Test. To determine absolute convergence, choose = 1 to get °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.6 ABSOLUTE CONVERGENCE AND THE RATIO AND ROOT TESTS ¤ 1011 lim →∞ = lim →∞ (1 2 + 4) = lim →∞ 2+ 4 2 = lim →∞ 1 + 4 12 = 1 0, so ∞=1 2+ 4 diverges by the Limit Comparison Test with the harmonic series. Thus, the series ∞ =1 (−1)−1 2 + 4 is conditionally convergent. 7. lim →∞ +1 = lim →∞ + 1 5+1 · 5 = lim →∞ 1 5 · + 1 = 1 5 lim →∞ 1 + 1 1 = 1 5 (1) = 1 5 1, so the series ∞ =1 5 is absolutely convergent by the Ratio Test. 8. lim →∞ +1 = lim →∞ (−2)+1 ( + 1)2 · 2 (−2) = lim →∞ (−2) 2 ( + 1)2 = 2 lim →∞ 1 (1 + 1)2 = 2(1) = 2 1, so the series ∞ =1 (−2) 2 is divergent by the Ratio Test. 9. lim →∞ +1 = lim →∞ (−1)3+1 2+1( + 1)3 · 23 (−1)−13 = lim →∞ −32 ( + 1) 3 3 = 3 2 lim →∞ (1 + 1 1)3 = 32(1) = 32 1, so the series ∞ =1 (−1)−1 3 23 is divergent by the Ratio Test. 10. lim →∞ +1 = lim →∞ (−3)+1 [2( + 1) + 1]! · (2 + 1)! (−3) = lim →∞ (−3) 1 (2 + 3)(2 + 2) = 3 lim →∞ 1 (2 + 3)(2 + 2) = 3(0) = 0 1 so the series ∞ =0 (−3) (2 + 1)! is absolutely convergent by the Ratio Test. 11. lim →∞ +1 = lim →∞ 1 ( + 1)! · ! 1 = lim →∞ 1 + 1 = 0 1, so the series ∞ =1 1 ! is absolutely convergent by the Ratio Test. Since the terms of this series are positive, absolute convergence is the same as convergence. 12. lim →∞ +1 = lim →∞ ( + 1)−(+1) − = lim →∞ + 1 · −1 = 1 lim →∞ 1 + 1 1 = 1(1) = 1 1, so the series ∞ =1 − is absolutely convergent by the Ratio Test. Since the terms of this series are positive, absolute convergence is the same as convergence. 13. lim →∞ +1 = lim →∞( + 2) 4 10+12+3 · ( + 1) 4 10 2+1 = lim →∞10 42 · + 1 + 2 = 58 1, so the series ∞=1 ( + 1)4 102+1 is absolutely convergent by the Ratio Test. Since the terms of this series are positive, absolute convergence is the same as convergence. 14. lim →∞ +1 = lim →∞(100 + 1)! +1 · 100 ! = lim →∞ 100 + 1 = ∞, so the series ∞=1 100 ! diverges by the Ratio Test. 15. lim →∞ +1 = lim →∞ ( + 1)+1 (−3) · (−3)−1 = lim →∞ −3 · + 1 = 3 lim →∞ 1 + 1 1 = 3 (1) = 3 1, so the series ∞ =1 (−3)−1 diverges by the Ratio Test. Or: Since lim →∞|| = ∞, the series diverges by the Test for Divergence. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1012 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 16. lim →∞ +1 = lim →∞ ( + 1)10 (−10)+2 · (−10)+1 10 = lim →∞ 1 −10 + 1 10 = 10 1 lim →∞1 + 1 10 = 10 1 (1) = 10 1 1, so the series ∞ =1 10 (−10)+1 is absolutely convergent by the Ratio Test. 17. lim →∞ +1 = lim →∞ cos[( + 1)3] ( + 1)! · ! cos(3) = lim →∞ cos[( + 1)3] ( + 1) cos(3) = lim →∞ + 1 = 0 1 (where 0 ≤ 2 for all positive integers ), so the series ∞ =1 cos(3) ! is absolutely convergent by the Ratio Test. 18. lim →∞ +1 = lim →∞ ( + 1)! ( + 1)+1 · ! = lim →∞ ( + 1) ( + 1)+1 = lim →∞ ( + 1) = lim →∞ (1 + 1 1) = 1 1, so the series ∞ =1 ! is absolutely convergent by the Ratio Test. 19. lim →∞ +1 = lim →∞ ( + 1)100100+1 ( + 1)! · ! 100100 = lim →∞ 100 + 1 + 1 100 = lim →∞ 100 + 1 1 + 1 100 = 0 · 1 = 0 1 so the series ∞ =1 100100 ! is absolutely convergent by the Ratio Test. 20. lim →∞ +1 = lim →∞ [2( + 1)]! [( + 1)!]2 · (!)2 (2)! = lim →∞ (2 + 2)(2 + 1) ( + 1)( + 1) = lim →∞ (2 + 2 (1 + 1 )(2 + 1 )(1 + 1 ) ) = 2 1 · · 2 1 = 4 1, so the series ∞ =1 (2)! (!)2 diverges by the Ratio Test. 21. lim →∞ +1 = lim →∞ (−1)( + 1)! 1 · 3 · 5 · · · · · (2 − 1)(2 + 1) · 1 · 3 · 5 · · · · · (2 − 1) (−1)−1! = lim →∞ + 1 2 + 1 = lim →∞ 1 + 1 2 + 1 = 1 2 1 so the series 1 − 2! 1 · 3 + 3! 1 · 3 · 5 − 4! 1 · 3 · 5 · 7 + · · · + (−1)−1 1 · 3 · 5 · · · · · ! (2 − 1) + · · · is absolutely convergent by the Ratio Test. 22. 2 3 + 2 · 5 3 · 5 + 2 · 5 · 8 3 · 5 · 7 + 2 · 5 · 8 · 11 3 · 5 · 7 · 9 + · · · = ∞ =1 2 · 5 · 8 · 11 · · · · · (3 − 1) 3 · 5 · 7 · 9 · · · · · (2 + 1) . lim →∞ +1 = lim →∞ 2 · 5 · 8 · · · · · (3 − 1)(3 + 2) 3 · 5 · 7 · · · · · (2 + 1)(2 + 3) · 3 · 5 · 7 · · · · · (2 + 1) 2 · 5 · 8 · · · · · (3 − 1) = lim →∞ 3 + 2 2 + 3 = lim →∞ 3 + 2 2 + 3 = 3 2 1 so the given series diverges by the Ratio Test. 23. lim →∞ +1 = lim →∞ 2 · 4 · 6 · · · · · (2)(2 + 2) ( + 1)! · ! 2 · 4 · 6 · · · · · (2) = lim →∞ 2 + 2 + 1 = lim →∞ 2( + 1) + 1 = 2 1, so the series ∞ =1 2 · 4 · 6 · · · · · (2) ! diverges by the Ratio Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.6 ABSOLUTE CONVERGENCE AND THE RATIO AND ROOT TESTS ¤ 1013 24. lim →∞ +1 = lim →∞ 2+1 ( + 1)! 5 · 8 · 11 · · · · · (3 + 2) (3 + 5) · 5 · 8 · 11 · · · · · (3 + 2) 2! = lim →∞ 2( + 1) 3 + 5 = 2 3 1, so the series ∞ =1 (−1) 2! 5 · 8 · 11 · · · · · (3 + 2) is absolutely convergent by the Ratio Test. 25. lim →∞ || = lim →∞ 2 + 1 22 + 1 = lim →∞ 1 + 1 2 + 1 2 2 = 12 1, so the series ∞=1 222+ 1 + 1 is absolutely convergent by the Root Test. 26. lim →∞ || = lim →∞ (−2) = lim →∞ 2 = 0 1, so the series ∞=1 (−2) is absolutely convergent by the Root Test. 27. lim →∞ || = lim →∞ ((ln −1))−1 = lim →∞ ln1 = 0 1, so the series ∞=2 ((ln −1))−1 is absolutely convergent by the Root Test. 28. lim →∞ || = lim →∞ −+ 1 2 5 = lim →∞ (25+ 1) 5 5 = 32 lim →∞ + 1 1 5 = 32 lim →∞ (1 + 1 1)5 = 32(1) = 32 1, so the series ∞ =1 −+ 1 2 5 diverges by the Root Test. 29. lim →∞ || = lim →∞ 1 + 1 2 = lim →∞1 + 1 = 1 [by Equation 3.6.6], so the series ∞=1 1 + 1 2 diverges by the Root Test. 30. lim →∞ || = lim →∞ |(arctan)| = lim →∞ arctan = 2 1, so the series ∞ =0 (arctan) diverges by the Root Test. 31. ∞ =2 (−1) ln converges by the Alternating Series Test since lim →∞ ln1 = 0 and ln1 is decreasing. Now ln , so 1 ln 1 , and since ∞ =2 1 is the divergent (partial) harmonic series, ∞ =2 1 ln diverges by the Comparison Test. Thus, ∞ =2 (−1) ln is conditionally convergent. 32. lim →∞ || = lim →∞ 2 + 3 1 − = lim →∞ 3−+ 2 1 = lim →∞ 1 3 + 2 − 1 = 13 1, so the series ∞=1 2 + 3 1 − is absolutely convergent by the Root Test. 33. lim →∞ +1 = lim →∞ (−9)+1 ( + 1)10+2 · 10+1 (−9) = lim →∞ (−9) 10( + 1) = 9 10 lim →∞ 1 1 + 1 = 9 10 (1) = 9 10 1, so the series ∞ =1 (−9) 10+1 is absolutely convergent by the Ratio Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1014 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 34. lim →∞ +1 = lim →∞ ( + 1)52+2 10+2 · 10+1 52 = lim →∞ 52( + 1) 10 = 5 2 lim →∞1 + 1 = 5 2(1) = 52 1, so the series ∞ =1 52 10+1 diverges by the Ratio Test. Or: Since lim →∞ = ∞, the series diverges by the Test for Divergence. 35. lim →∞ || = lim →∞ ln = lim →∞ ln = lim →∞ ln = lim H →∞ 1 1 = lim →∞ = ∞, so the series ∞ =2 ln diverges by the Root Test. 36. sin(6) 1 + √ ≤ 1 1 + √ 1 32 , so the series ∞ =1 sin(6) 1 + √ converges by comparison with the convergent -series ∞ =1 1 32 ( = 3 2 1). It follows that the given series is absolutely convergent. 37. (−1) arctan 2 2 2 , so since ∞ =1 2 2 = 2 ∞ =1 1 2 converges ( = 2 1), the given series ∞ =1 (−1) arctan 2 converges absolutely by the Comparison Test. 38. The function () = 1 ln is continuous, positive, and decreasing on [2 ∞). 2∞ ln 1 = lim →∞2 ln 1 = lim →∞[ln(ln)] 2 = lim →∞[(ln(ln) − ln(ln 2)] = ∞, so the series ∞ =2 (−1) ln diverges by the Integral Test. Now {} = ln 1 with ≥ 2 is a decreasing sequence of positive terms and lim →∞ = 0. Thus, ∞ =2 (−1) ln converges by the Alternating Series Test. It follows that ∞ =2 (−1) ln is conditionally convergent. 39. By the recursive definition, lim →∞ +1 = lim →∞ 5 + 1 4 + 3 = 5 4 1, so the series diverges by the Ratio Test. 40. By the recursive definition, lim →∞ +1 = lim →∞ 2 + cos √ = 0 1, so the series converges absolutely by the Ratio Test. 41. The series ∞ =1 cos = ∞ =1 (−1) , where 0 for ≥ 1 and lim →∞ = 1 2 . lim →∞ +1 = lim →∞ (−1)+1 +1 + 1 · (−1) = lim →∞ + 1 = 1 2 (1) = 1 2 1, so the series ∞ =1 cos is absolutely convergent by the Ratio Test. 42. lim →∞ +1 = lim →∞ (−1)+1( + 1)! ( + 1)+112 · · · +1 · 12 · · · (−1) ! = lim →∞ (−1)( + 1) +1( + 1)+1 = lim →∞ +1( + 1) = lim →∞ 1 +1 + 1 = lim →∞ 1+1 1 + 1 1 = lim →∞ +1(1 + 1 1 ) = 1 21 = 2 1 so the series ∞ =1 (−1) ! 123 · · · is absolutely convergent by the Ratio Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.6 ABSOLUTE CONVERGENCE AND THE RATIO AND ROOT TESTS ¤ 1015 43. (a) lim →∞ 1( + 1)3 13 = lim →∞ 3 ( + 1)3 = lim →∞ (1 + 1 1)3 = 1. Inconclusive (b) lim →∞ ( + 1) 2+1 · 2 = lim →∞ + 1 2 = lim →∞1 2 + 21 = 12. Conclusive (convergent) (c) lim →∞ (−3) √ + 1 · √ (−3)−1 = 3 lim →∞ + 1 = 3 lim →∞1 + 1 1 = 3. Conclusive (divergent) (d) lim →∞ √ + 1 1 + ( + 1)2 · 1 + 2 √ = lim →∞1 + 1 · 121+ (1 + 1 2 + 1)2 = 1. Inconclusive 44. We use the Ratio Test: lim →∞ +1 = lim →∞ [( + 1)!]2/[( + 1)]! (!)2/()! = lim →∞ ( + 1)2 [( + 1)] [( + 1) − 1]· · ·[ + 1] Now if = 1, then this is equal to lim →∞ ( + 1)2 ( + 1) = ∞, so the series diverges; if = 2, the limit is lim →∞ ( + 1)2 (2 + 2)(2 + 1) = 1 4 1, so the series converges, and if 2, then the highest power of in the denominator is larger than 2, and so the limit is 0, indicating convergence. So the series converges for ≥ 2. 45. (a) lim →∞ +1 = lim →∞ +1 ( + 1)! · ! = lim →∞ + 1 = || lim →∞ 1 + 1 = || · 0 = 0 1, so by the Ratio Test the series ∞ =0 ! converges for all . (b) Since the series of part (a) always converges, we must have lim →∞ ! = 0 by Theorem 11.2.6. 46. (a) = +1 + +2 + +3 + +4 + · · · = +11 + +2 +1 + +3 +1 + +4 +1 + · · · = +11 + +2 +1 + +3 +2 +2 +1 + +4 +3 +3 +2 +2 +1 + · · · = +1(1 + +1 + +2+1 + +3+2+1 + · · ·) () ≤ +11 + +1 + 2 +1 + 3 +1 + · · · [since {} is decreasing] = 1 −+1 +1 (b) Note that since {} is increasing and → as → ∞, we have for all . So, starting with equation (), = +1(1 + +1 + +2+1 + +3+2+1 + · · ·) ≤ +11 + + 2 + 3 + · · · = 1−+1 . 47. (a) 5 = 5 =1 1 2 = 1 2 + 1 8 + 1 24 + 1 64 + 1 160 = 661 960 ≈ 068854. Now the ratios = +1 = 2 ( + 1)2+1 = 2( + 1) form an increasing sequence, since +1 − = + 1 2( + 2) − 2( + 1) = ( + 1)2 − ( + 2) 2( + 1)( + 2) = 1 2( + 1)( + 2) 0. So by Exercise 46(b), the error in using 5 is 5 ≤ 6 1 − lim →∞ = 16 · 26 1 − 12 = 1 192 ≈ 000521. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1016 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES (b) The error in using as an approximation to the sum is = +1 1 − 1 2 = 2 ( + 1)2+1 . We want 000005 ⇔ 1 ( + 1)2 000005 ⇔ ( + 1)2 20,000. To find such an we can use trial and error or a graph. We calculate (11 + 1)211 = 24,576, so 11 = 11 =1 1 2 ≈ 0693109 is within 000005 of the actual sum. 48. 10 = 10 =1 2 = 1 2 + 2 4 + 3 8 + · · · + 10 1024 ≈ 1988. The ratios = +1 = 2+ 1 +1 · 2 = 2+ 1 = 121 + 1 form a decreasing sequence, and 11 = 11 + 1 2(11) = 12 22 = 6 11 1, so by Exercise 46(a), the error in using 10 to approximate the sum of the series ∞ =1 2 is 10 ≤ 11 1 − 11 = 11 2048 1 − 6 11 = 121 10,240 ≈ 00118. 49. (i) Following the hint, we get that || for ≥ , and so since the geometric series ∞ =1 converges [0 1], the series ∞ = || converges as well by the Comparison Test, and hence so does ∞ =1 ||, so ∞ =1 is absolutely convergent. (ii) If lim →∞ || = 1, then there is an integer such that || 1 for all ≥ , so || 1 for ≥ . Thus, lim →∞ 6= 0, so ∞ =1 diverges by the Test for Divergence. (iii) Consider ∞ =1 1 [diverges] and ∞ =1 1 2 [converges]. For each sum, lim →∞ || = 1, so the Root Test is inconclusive. 50. (a) lim →∞ +1 = lim →∞ [4( + 1)]! [1103 + 26,390( + 1)] [( + 1)!]4 3964(+1) · (!)4 3964 (4)! (1103 + 26,390) = lim →∞ (4 + 4)(4 + 3)(4 + 2)(4 + 1)(26,390 + 27,493) ( + 1)4 3964 (26,390 + 1103) = 44 3964 = 1 994 1, so by the Ratio Test, the series ∞ =0 (4)! (1103 + 26,390) (!)4 3964 converges. (b) 1 = 2√2 9801 ∞ =0 (4)! (1103 + 26,390) (!)4 3964 With the first term ( = 0), 1 ≈ 2√2 9801 · 1103 1 ⇒ ≈ 3141 592 73, so we get 6 correct decimal places of , which is 3141 592 653 589 793 238 to 18 decimal places. With the second term ( = 1), 1 ≈ 2√2 9801 1103 1 + 4! (1103 + 26 3964 ,390) ⇒ ≈ 3141592653589793878, so we get 15 correct decimal places of . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.6 ABSOLUTE CONVERGENCE AND THE RATIO AND ROOT TESTS ¤ 1017 51. (a) Since is absolutely convergent, and since + ≤ || and − ≤ || (because + and − each equal either or 0), we conclude by the Comparison Test that both + and − must be absolutely convergent. Or: Use Theorem 11.2.8. (b) We will show by contradiction that both + and − must diverge. For suppose that + converged. Then so would + − 1 2 by Theorem 11.2.8. But + − 1 2 = 1 2 ( + ||) − 1 2 = 1 2 ||, which diverges because is only conditionally convergent. Hence, + can’t converge. Similarly, neither can − . 52. Let be the rearranged series constructed in the hint. [This series can be constructed by virtue of the result of Exercise 51(b).] This series will have partial sums that oscillate in value back and forth across . Since lim →∞ = 0 (by Theorem 11.2.6), and since the size of the oscillations | − | is always less than || because of the way was constructed, we have that = lim →∞ = . 53. Suppose that is conditionally convergent. (a) 2 is divergent: Suppose 2 converges. Then lim →∞ 2 = 0 by Theorem 6 in Section 11.2, so there is an integer 0 such that ⇒ 2 || 1. For , we have || 1 2 , so || converges by comparison with the convergent -series 1 2 . In other words, converges absolutely, contradicting the assumption that is conditionally convergent. This contradiction shows that 2 diverges. Remark: The same argument shows that diverges for any 1. (b) ∞ =2 (−1) ln is conditionally convergent. It converges by the Alternating Series Test, but does not converge absolutely by the Integral Test, since the function () = ln 1 is continuous, positive, and decreasing on [2 ∞) and 2∞ ln = lim →∞ 2 ln = lim →∞ ln(ln) 2 = ∞. Setting = (−ln1) for ≥ 2, we find that ∞ =2 = ∞ =2 (−1) ln converges by the Alternating Series Test. It is easy to find conditionally convergent series such that diverges. Two examples are ∞ =1 (−1)−1 and ∞ =1 (−1)−1 √ , both of which converge by the Alternating Series Test and fail to converge absolutely because || is a -series with ≤ 1. In both cases, diverges by the Test for Divergence. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1018 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 11.7 Strategy for Testing Series 1. Use the Limit Comparison Test with = 2 − 1 3 + 1 and = 1 : lim →∞ = lim →∞ (23−+ 1 1) = lim →∞ 33 −+ 1 = lim →∞ 1 1 + 1 − 1 / 2 3 = 1 0. Since ∞=1 1 is the divergent harmonic series, the series ∞ =1 2 − 1 3 + 1 also diverges. 2. − 1 3 + 1 3 + 1 3 = 1 2 for ≥ 1, so ∞ =1 − 1 3 + 1 converges by comparison with ∞ =1 1 2 , which converges because it is a p-series with = 2 1. 3. ∞ =1 (−1) 2 − 1 3 + 1 = ∞ =1 (−1). Now = 2 − 1 3 + 1 0 for ≥ 2, {} is decreasing for ≥ 2, and lim →∞ = 0, so the series ∞ =1 (−1) 2 − 1 3 + 1 converges by the Alternating Series Test. By Exercise 1, ∞ =1 2 − 1 3 + 1 diverges, so the series ∞ =1 (−1) 2 − 1 3 + 1 is conditionally convergent. 4. lim →∞ || = lim →∞ (−1) 2 − 1 2 + 1 = lim →∞ 1 − 12 1 + 12 = 1 6= 0, so the series ∞ =1 (−1) 2 − 1 2 + 1 diverges by the Test for Divergence. Note that lim →∞(−1) 2 2 − + 1 1 does not exist. 5. lim →∞ 2 H = lim →∞ 2 H = lim →∞ 2 = ∞, so lim →∞ 2 = ∞. Thus, the series ∞ =1 2 diverges by the Test for Divergence. 6. lim →∞ || = lim →∞ (1 +2)3 = lim →∞ (1 +2)3 = lim →∞ (11 + 1)3 = 0 1 = 0 1, so the series ∞=1 (1 +2)3 converges by the Root Test. 7. Let () = 1 √ln. Then is positive, continuous, and decreasing on [2 ∞), so we can apply the Integral Test. Since √1ln == ln , = −12 = 212 + = 2√ln + , we find 2∞ √ln = lim →∞2 √ln = lim →∞2√ln 2 = lim →∞2√ln − 2√ln 2 = ∞. Since the integral diverges, the given series ∞ =2 1 √ln diverges. 8. lim →∞ +1 = lim →∞ ( + 1)4 4+1 · 4 4 = lim →∞ ( + 1)4 44 = 1 4 lim →∞1 + 1 4 = 1 4(1) = 14 1, so the series ∞ =1 (−1)−1 4 4 is absolutely convergent (and therefore convergent) by the Ratio Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.7 STRATEGY FOR TESTING SERIES ¤ 1019 9. lim →∞ +1 = lim →∞ 2+2 (2 + 2)! · (2)! 2 = lim →∞ 2 (2 + 2)(2 + 1) = 0 1, so the series ∞ =0 (−1) 2 (2)! is absolutely convergent (and therefore convergent) by the Ratio Test. 10. Let () = 2−3. Then is continuous and positive on [1 ∞), and 0() = (2 − 33) 3 0 for ≥ 1, so is decreasing on [1 ∞) as well, and we can apply the Integral Test. 1∞ 2−3 = lim →∞− 1 3−3 1 = 31, so the integral converges, and hence, the series converges. 11. ∞ =1 13 + 31 = ∞=1 13 + ∞=1 1 3. The first series converges since it is a -series with = 3 1 and the second series converges since it is geometric with || = 1 3 1. The sum of two convergent series is convergent. 12. 1 √2 + 1 1 √2 = 1 2 , so ∞ =1 1 √2 + 1 converges by comparison with the convergent -series ∞ =1 1 2 ( = 2 1). 13. lim →∞ +1 = lim →∞ 3+1 ( + 1)2 ( + 1)! · ! 32 = lim →∞ 3( + 1)2 ( + 1)2 = 3 lim →∞ + 1 2 = 0 1, so the series ∞=1 3! 2 converges by the Ratio Test. 14. sin 2 1 + 2 ≤ 1 1 + 2 1 2 = 1 2, so the series ∞=1 1 + 2 sin 2 converges by comparison with the geometric series ∞ =1 1 2 with || = 1 2 1. Thus, the series ∞=1 1 + 2 sin 2 converges absolutely, implying convergence. 15. = 2−13+1 = 22−1331 = 3 2 2· 3. By the Root Test, lim →∞ 6 = lim →∞ 6 = 0 1, so the series ∞ =1 6 converges. It follows from Theorem 8(i) in Section 11.2 that the given series, ∞=1 2−13+1 = ∞=1 3 26, also converges. 16. Use the Limit Comparison Test with = √4 + 1 3 + and = 1 : lim →∞ = lim →∞ √(24+ 1) + 1 = lim →∞ √(24+ 1) + 1 22 = lim →∞ 1 + 1 1 + 1 2 4 = 1 0. Since ∞=1 1 is the divergent harmonic series, the series ∞ =1 √4 + 1 3 + also diverges. 17. lim →∞ +1 = lim →∞ 1 · 3 · 5 · · · · · (2 − 1)(2 + 1) 2 · 5 · 8 · · · · · (3 − 1)(3 + 2) · 2 · 5 · 8 · · · · · (3 − 1) 1 · 3 · 5 · · · · · (2 − 1) = lim →∞ 2 + 1 3 + 2 = lim →∞ 2 + 1 3 + 2 = 2 3 1 so the series ∞ =1 1 · 3 · 5 · · · · · (2 − 1) 2 · 5 · 8 · · · · · (3 − 1) converges by the Ratio Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1020 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 18. = √1− 1 for ≥ 2. {} is a decreasing sequence of positive numbers and lim →∞ = 0, so ∞=2 (√−1)−−11 converges by the Alternating Series Test. 19. Let () = ln √. Then 0() = 22−3ln 2 0 when ln 2 or 2, so ln √ is decreasing for 2. By l’Hospital’s Rule, lim →∞ ln √ = lim →∞ 112 √ = lim →∞ √2 = 0, so the series ∞=1(−1) ln √ converges by the Alternating Series Test. 20. = √3 − 1 (√ + 1) √3 (√ + 1) √3 √ = 13 32 = 1 76 , so the series ∞ =1 √3 − 1 (√ + 1) converges by comparison with the convergent -series ∞ =1 1 76 = 7 6 1. 21. lim →∞ || = lim →∞ (−1) cos(12) = lim →∞ cos(12) = cos 0 = 1, so the series ∞ =1 (−1) cos(12) diverges by the Test for Divergence. 22. lim →∞ || = lim →∞ 1 2 + sin = lim →∞ 1 2 + sin , which does not exist (the terms vary between 1 3 and 1). Thus, the series ∞ =1 1 2 + sin diverges by the Test for Divergence. 23. Using the Limit Comparison Test with = tan1 and = 1 , we have lim →∞ = lim →∞ tan(1 1) = lim →∞ tan(1 1) = lim H →∞ sec2(1 −1) · (2−12) = lim →∞sec2(1) = 12 = 1 0. Since ∞ =1 is the divergent harmonic series, ∞ =1 is also divergent. 24. lim →∞ = lim →∞sin 1 = lim →∞ sin(1 1) = lim →0+ sin = 1 6= 0, so the series ∞=1 sin(1) diverges by the Test for Divergence. 25. Use the Ratio Test. lim →∞ +1 = lim →∞ ( + 1)! (+1)2 · 2 ! = lim →∞ ( + 1)! · 2 2+2+1! = lim →∞ 2+ 1 +1 = 0 1, so ∞=1 !2 converges. 26. lim →∞ +1 = lim →∞ +1 = lim →∞2 + 2 5+1 + 2 · 25+ 1 = lim →∞1 + 2 1 + 1 + 2 22 · 15 = 1 5 1, so ∞=1 25+ 1 converges by the Ratio Test. 27. 2∞ ln 2 = lim →∞−ln − 1 1 [using integration by parts] = 1 H . So ∞=1 ln2 converges by the Integral Test, and since ln ( + 1)3 ln 3 = ln 2 , the given series ∞ =1 ln ( + 1)3 converges by the Comparison Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.7 STRATEGY FOR TESTING SERIES ¤ 1021 28. Since 1 is a decreasing sequence, 1 ≤ 11 = for all ≥ 1, and ∞=1 2 converges ( = 2 1), so ∞=1 1 2 converges by the Comparison Test. (Or use the Integral Test.) 29. ∞ =1 = ∞ =1 (−1) 1 cosh = ∞ =1 (−1) . Now = 1 cosh 0, {} is decreasing, and lim →∞ = 0, so the series converges by the Alternating Series Test. Or: Write 1 cosh = 2 + − 2 and ∞ =1 1 is a convergent geometric series, so ∞ =1 1 cosh is convergent by the Comparison Test. So ∞ =1 (−1) 1 cosh is absolutely convergent and therefore convergent. 30. Let () = √ + 5 . Then () is continuous and positive on [1 ∞), and since 0() = 5 − 2√( + 5)2 0 for 5, () is eventually decreasing, so we can use the Alternating Series Test. lim →∞ √ + 5 = lim →∞ 1 12 + 5−12 = 0, so the series ∞ =1 (−1) √ + 5 converges. 31. lim →∞ = lim →∞ 5 3 + 4 = [divide by 4] lim →∞ (3(5 4) 4) + 1 = ∞ since lim →∞3 4 = 0 and lim →∞5 4 = ∞. Thus, ∞ =1 5 3 + 4 diverges by the Test for Divergence. 32. lim →∞ || = lim →∞ (4!) = lim →∞ 4! = lim →∞ · − 1 · − 2 · − 3 · ( − 4)! = lim →∞1 − 1 1 − 2 1 − 3 ( − 4)! = ∞, so the series ∞ =1 (!) 4 diverges by the Root Test. 33. lim →∞ || = lim →∞ + 1 2 = lim →∞ [( + 1) 1 ] = lim 1 →∞ (1 + 1) = 1 1, so the series ∞ =1 + 1 2 converges by the Root Test. 34. 0 ≤ cos2 ≤ , so 1 + cos2 ≥ +1 = 21. Thus, ∞=1 + 1cos2 diverges by comparison with ∞=1 21, which is a constant multiple of the (divergent) harmonic series. 35. = 1 1+1 = 1 · 1 , so let = 1 and use the Limit Comparison Test. lim →∞ = lim →∞ 11 = 1 0 [see Exercise 4.4.63], so the series ∞ =1 1 1+1 diverges by comparison with the divergent harmonic series. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1022 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 36. Note that (ln)ln = ln ln ln = ln ln ln = ln ln and ln ln → ∞ as → ∞, so ln ln 2 for sufficiently large . For these we have (ln)ln 2, so 1 (ln)ln 1 2 . Since ∞ =2 1 2 converges [ = 2 1], so does ∞ =2 1 (ln)ln by the Comparison Test. 37. lim →∞ || = lim →∞ (21 − 1) = 1 − 1 = 0 1, so the series ∞ =1 √ 2 − 1 converges by the Root Test. 38. Use the Limit Comparison Test with = √ 2 − 1 and = 1. Then lim →∞ = lim →∞ 21 1− 1 = lim →∞ 21 1− 1 = lim H →∞ 21 · ln 2 −1 · (2−12) = lim →∞(21 · ln 2) = 1 · ln 2 = ln 2 0. So since ∞ =1 diverges (harmonic series), so does ∞ =1 √ 2 − 1. Alternate solution: √ 2 − 1 = 1 2(−1) + 2(−2) + 2(−3) + · · · + 21 + 1 [rationalize the numerator] ≥ 21, and since ∞ =1 1 2 = 1 2 ∞ =1 1 diverges (harmonic series), so does ∞ =1 √ 2 − 1 by the Comparison Test. 11.8 Power Series 1. A power series is a series of the form ∞ =0 = 0 + 1 + 22 + 33 + · · · , where is a variable and the ’s are constants called the coefficients of the series. More generally, a series of the form ∞ =0 ( − ) = 0 + 1( − ) + 2( − )2 + · · · is called a power series in ( − ) or a power series centered at or a power series about , where is a constant. 2. (a) Given the power series ∞ =0 ( − ), the radius of convergence is: (i) 0 if the series converges only when = (ii) ∞ if the series converges for all , or (iii) a positive number such that the series converges if | − | and diverges if | − | . In most cases, can be found by using the Ratio Test. (b) The interval of convergence of a power series is the interval that consists of all values of for which the series converges. Corresponding to the cases in part (a), the interval of convergence is: (i) the single point {}, (ii) all real numbers; that is, the real number line (−∞ ∞), or (iii) an interval with endpoints − and + which can contain neither, either, or both of the endpoints. In this case, we must test the series for convergence at each endpoint to determine the interval of convergence. 3. If = (−1), then lim →∞ +1 = lim →∞ (−1)+1( + 1)+1 (−1) = lim →∞ (−1) + 1 = lim →∞1 + 1 || = ||. By the Ratio Test, the series ∞ =1 (−1) converges when || 1, so the radius of convergence = 1. Now we’ll check the endpoints, that is, °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.8 POWER SERIES ¤ 1023 = ±1. Both series ∞ =1 (−1)(±1) = ∞ =1 (∓1) diverge by the Test for Divergence since lim →∞ |(∓1)| = ∞. Thus, the interval of convergence is = (−1 1). 4. If = (−1) √3 , then lim →∞ +1 = lim →∞ (−1)+1+1 √3 + 1 · √3 (−1) = lim →∞ (−1)√3 √3 + 1 = lim →∞ 3 1 + 1 1 || = ||. By the Ratio Test, the series ∞ =1 (−1) √3 converges when || 1, so = 1. When = 1, the series ∞ =1 (−1) √3 converges by the Alternating Series Test. When = −1, the series ∞ =1 1 √3 diverges since it is a -series = 1 3 ≤ 1. Thus, the interval of convergence is (−11]. 5. If = 2 − 1 , then lim →∞ +1 = lim →∞ +1 2 + 1 · 2 − 1 = lim →∞2 2 − + 1 1 || = lim →∞2 2 + 1 − 1 || = ||. By the Ratio Test, the series ∞ =1 2 − 1 converges when || 1, so = 1. When = 1, the series ∞ =1 1 2 − 1 diverges by comparison with ∞ =1 1 2 since 1 2 − 1 1 2 and 1 2 ∞ =1 1 diverges since it is a constant multiple of the harmonic series. When = −1, the series ∞ =1 (−1) 2 − 1 converges by the Alternating Series Test. Thus, the interval of convergence is [−11). 6. If = (−1) 2 , then lim →∞ +1 = lim →∞ (−1)+1+1 ( + 1)2 · 2 (−1) = lim →∞ (−1)2 ( + 1)2 = lim →∞ + 1 2 || = 12 · || = ||. By the Ratio Test, the series ∞ =1 (−1) 2 converges when || 1, so = 1. When = 1, the series ∞ =1 (−1) 2 converges by the Alternating Series Test. When = −1, the series ∞ =1 1 2 converges since it is a -series with = 2 1. Thus, the interval of convergence is [−11]. 7. If = ! , then lim →∞ +1 = lim →∞ +1 ( + 1)! · ! = lim →∞ + 1 = || lim →∞ 1 + 1 = || · 0 = 0 1 for all real . So, by the Ratio Test, = ∞ and = (−∞ ∞). 8. Here the Root Test is easier. If = , then lim →∞ || = lim →∞ || = ∞ if 6= 0, so = 0 and = {0}. 9. If = 4 4 , then lim →∞ +1 = lim →∞ +1 ( + 1)4 4+1 · 4 4 = lim →∞ 4 ( + 1)4 · 4 = lim →∞ + 1 4 |4| = 14 · |4| = |4|. By the Ratio Test, the series ∞ =1 4 4 converges when |4| 1 ⇔ || 4 , so = 4. When = 4, the series ∞ =1 1 4 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1024 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES converges since it is a p-series ( = 4 1). When = −4, the series ∞ =1 (−1) 4 converges by the Alternating Series Test. Thus, the interval of convergence is [−44]. 10. If = 22, then lim →∞ +1 = lim →∞ 2+1( + 1)2+1 22 = lim →∞ 2 + 1 2 || = 2||. By the Ratio Test, the series ∞ =1 22 converges when 2|| 1 ⇔ || 1 2 , so = 1 2 . When = ± 1 2 , both series ∞ =1 22± 1 2 = ∞ =1 (±1)2 diverge by the Test for Divergence since lim →∞ (±1)2 = ∞. Thus, the interval of convergence is − 1 2 1 2. 11. If = (−1) √ 4 , then lim →∞ +1 = lim →∞ (−1)√+14+ 1 +1 +1 · (−1)√4 = lim →∞ + 1 · 4|| = 4||. By the Ratio Test, the series ∞ =1 (−1) 4 √ converges when 4|| 1 ⇔ || 1 4 , so = 1 4 . When = 1 4 , the series ∞ =1 (−1) √ converges by the Alternating Series Test. When = − 1 4 , the series ∞ =1 1 √ diverges since it is a p-series = 1 2 ≤ 1. Thus, the interval of convergence is − 1 4 1 4. 12. If = ∞ =1 (−1)−1 5 , then lim →∞ +1 = lim →∞ (−1)+1 ( + 1) 5+1 · 5 (−1)−1 = lim →∞ + 1 |5| = 1 · |5| = |5| . By the Ratio Test, the series ∞ =1 (−1)−1 5 converges when || 5 1 ⇔ || 5, so = 5. When = 5, the series ∞ =1 (−1)−1 converges by the Alternating Series Test. When = −5, the series ∞ =1 −1 diverges since it is a constant multiple of the harmonic series. Thus, the interval of convergence is (−5 5]. 13. If = 2(2 + 1) , then lim →∞ +1 = lim →∞ ( + 1)+1 2+1(2 + 2 + 2) · 2(2 + 1) = lim →∞ 3 + 2 + + 1 3 + 22 + 2 · || 2 = lim →∞ 1 + 1 + 12 + 13 1 + 2 + 22 · || 2 = || 2 By the Ratio Test, the series ∞ =1 2(2 + 1) converges when |2| 1 ⇔ || 2, so = 2. When = 2 the series ∞ =1 2 + 1 diverges by the Limit Comparison Test with = 1 . When = −2, the series ∞=1 (−21) + 1 converges by the Alternating Series Test. Thus, the interval of convergence is [−2 2). 14. If = 2 ! , then lim →∞ +1 = lim →∞ 2+2 ( + 1)! · ! 2 = lim →∞ 2 + 1 = 0 1 for all real So, by the Ratio Test, = ∞ and = (−∞ ∞). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.8 POWER SERIES ¤ 1025 15. If = ( − 2) 2 + 1 , then lim →∞ +1 = lim →∞ ( − 2)+1 ( + 1)2 + 1 · 2 + 1 ( − 2) = | − 2| lim →∞ 2 + 1 ( + 1)2 + 1 = | − 2|. By the Ratio Test, the series ∞ =0 ( − 2) 2 + 1 converges when | − 2| 1 [ = 1] ⇔ −1 − 2 1 ⇔ 1 3. When = 1, the series ∞ =0 (−1) 1 2 + 1 converges by the Alternating Series Test; when = 3, the series ∞ =0 1 2 + 1converges by comparison with the p-series ∞ =1 1 2 [ = 2 1]. Thus, the interval of convergence is = [1 3]. 16. If = (−1) (2 − 1)2 ( − 1), then lim →∞ +1 = lim →∞ (−1)+1( − 1)+1 (2 + 1) 2+1 · (2 − 1)2 (−1)( − 1) = lim →∞ 2 − 1 2 + 1 · | − 1| 2 = | − 1| 2 . By the Ratio Test, the series ∞ =1 (−1) (2 − 1)2 ( − 1) converges when | −2 1| 1 ⇔ | − 1| 2 [ = 2] ⇔ −2 − 1 2 ⇔ −1 3. When = 3, the series ∞ =1 (−1) 2 − 1 converges by the Alternating Series Test. When = −1, the series ∞ =1 1 2 − 1 diverges by the Limit Comparison Test with = 1 . Thus, the interval of convergence is (−13]. 17. If = ( + 2) 2 ln , then lim →∞ ( + 2)+1 2+1 ln( + 1) · 2 ln ( + 2) = lim →∞ ln ln( + 1) · | + 2| 2 = | + 2| 2 since lim →∞ ln ln( + 1) = lim →∞ ln(ln+ 1) = lim H →∞ 1(1 + 1) = lim →∞ + 1 = lim →∞1 + 1 = 1. By the Ratio Test, the series ∞ =2 ( + 2) 2 ln converges when | + 2 2 | 1 ⇔ | + 2| 2 [ = 2] ⇔ −2 + 2 2 ⇔ −4 0. When = −4, the series ∞ =2 (−1) ln converges by the Alternating Series Test. When = 0, the series ∞ =2 1 ln diverges by the Limit Comparison Test with = 1 (or by comparison with the harmonic series). Thus, the interval of convergence is [−40). 18. If = √ 8 ( + 6), then lim →∞ +1 = lim →∞ √ + 1( + 6)+1 8+1 · 8 √( + 6) = lim →∞ + 1 · | + 6 8 | = lim →∞1 + 1 · | + 6 8 | = | + 6 8 | By the Ratio Test, the series ∞ =1 √ 8 ( + 6) converges when | + 6| 8 1 ⇔ | + 6| 8 [ = 8] ⇔ −8 + 6 8 ⇔ −14 2. When = 2, the series ∞ =1 √ diverges by the Test for Divergence since lim →∞ || = lim →∞ √ = ∞ 0. Similarly, when = −14, the series ∞ =1 (−1)√ diverges. Thus, the interval of convergence is (−14 2). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1026 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 19. If = ( − 2) , then lim →∞ || = lim →∞ | − 2| = 0, so the series converges for all (by the Root Test). = ∞ and = (−∞ ∞). 20. If = (2 − 1) 5√ , then lim →∞ +1 = lim →∞ (2 − 1)+1 5+1√ + 1 · 5√ (2 − 1) = lim →∞ |2 − 1| 5 + 1 = lim →∞ |25− 1|1 + 1 1 = |25− 1|. By the Ratio Test, the series ∞ =1 (2 − 1) 5√ converges when |25− 1| 1 ⇔ |2 − 1| 5 ⇔ − 1 2 5 2 ⇔ − 5 2 − 1 2 5 2 ⇔ −2 3, so = 5 2. When = 3, the series ∞ =1 1 √ is a divergent -series = 1 2 ≤ 1. When = −2, the series ∞ =1 (−1) √ converges by the Alternating Series Test. Thus, the interval of convergence is = [−23). 21. = ( − ), where 0. lim →∞ +1 = lim →∞ ( + 1)| − |+1 +1 · | − | = lim →∞1 + 1 | − | = | − |. By the Ratio Test, the series converges when | − | 1 ⇔ | − | [so = ] ⇔ − − ⇔ − + . When | − | = , lim →∞ || = lim →∞ = ∞, so the series diverges. Thus, = ( − + ). 22. = ln( − ), where 0. lim →∞ +1 = lim →∞ +1( − )+1 ln( + 1) · ln ( − ) = lim →∞ ln ln( + 1) · | − | = | − | since lim →∞ ln ln( + 1) = lim →∞ ln(ln + 1) = lim H →∞ 1(1 + 1) = lim →∞ + 1 = lim H →∞ 1 1 = 1. By the Ratio Test, the series ∞ =2 ln( − ) converges when | − | 1 ⇔ | − | 1 ⇔ −1 − 1 ⇔ − 1 + 1 , so = 1 . When = + 1 , the series ∞ =2 1 ln diverges by comparison with the divergent -series ∞ =2 1 since 1 ln 1 for ≥ 2. When = − 1 , the series ∞ =2 (−1) ln converges by the Alternating Series Test. Thus, the interval of convergence is = − 1 + 1 . 23. If = ! (2 − 1), then lim →∞ +1 = lim →∞ ( + 1)!(2 − 1)+1 !(2 − 1) = lim →∞ ( + 1)|2 − 1| → ∞ as → ∞ for all 6= 1 2. Since the series diverges for all 6= 1 2, = 0 and = 1 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.8 POWER SERIES ¤ 1027 24. = 2 2 · 4 · 6 · · · · · (2) = 2 2! = 2( − 1)!, so lim →∞ +1 = lim →∞ ( + 1)||+1 2+1! · 2( − 1)! || = lim →∞ + 1 2 |2| = 0. Thus, by the Ratio Test, the series converges for all real and we have = ∞ and = (−∞ ∞). 25. If = (5 − 4) 3 , then lim →∞ +1 = lim →∞ (5 − 4)+1 ( + 1)3 · 3 (5 − 4) = lim →∞ |5 − 4| + 1 3 = lim →∞|5 − 4| 1 + 1 1 3 = |5 − 4| · 1 = |5 − 4| By the Ratio Test, ∞ =1 (5 − 4) 3 converges when |5 − 4| 1 ⇔ − 4 5 1 5 ⇔ − 1 5 − 4 5 1 5 ⇔ 3 5 1, so = 1 5 . When = 1, the series ∞ =1 1 3 is a convergent -series ( = 3 1). When = 3 5 , the series ∞ =1 (−1) 3 converges by the Alternating Series Test. Thus, the interval of convergence is = 3 51. 26. If = 2 (ln)2 , then lim →∞ +1 = lim →∞ 2+2 ( + 1)[ln( + 1)]2 · (ln)2 2 = 2 lim →∞ (ln)2 ( + 1)[ln( + 1)]2 = 2. By the Ratio Test, the series ∞ =2 2 (ln)2 converges when 2 1 ⇔ || 1, so = 1. When = ±1, 2 = 1, the series ∞ =2 1 (ln)2 converges by the Integral Test (see Exercise 11.3.22). Thus, the interval of convergence is = [−1 1]. 27. If = 1 · 3 · 5 · · · · · (2 − 1), then lim →∞ +1 = lim →∞ +1 1 · 3 · 5 · · · · · (2 − 1)(2 + 1) · 1 · 3 · 5 · · · · · (2 − 1) = lim →∞ || 2 + 1 = 0 1. Thus, by the Ratio Test, the series ∞ =1 1 · 3 · 5 · · · · · (2 − 1) converges for all real and we have = ∞ and = (−∞ ∞). 28. If = ! 1 · 3 · 5 · · · · · (2 − 1), then lim →∞ +1 = lim →∞ ( + 1)!+1 1 · 3 · 5 · · · · · (2 − 1)(2 + 1) · 1 · 3 · 5 · · · · · (2 − 1) ! = lim →∞ ( + 1)|| 2 + 1 = 1 2 ||. By the Ratio Test, the series ∞ =1 converges when 1 2 || 1 ⇒ || 2 so = 2. When = ±2, || = !2 1 · 3 · 5 · · · · · (2 − 1) = [1 · 2 · 3 · · · · · ]2 [1 · 3 · 5 · · · · · (2 − 1)] = 2 · 4 · 6 · · · · · 2 1 · 3 · 5 · · · · · (2 − 1) 1, so both endpoint series diverge by the Test for Divergence. Thus, the interval of convergence is = (−22). 29. (a) We are given that the power series ∞ =0 is convergent for = 4. So by Theorem 4, it must converge for at least −4 ≤ 4. In particular, it converges when = −2; that is, ∞ =0 (−2) is convergent. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1028 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES (b) It does not follow that ∞ =0 (−4) is necessarily convergent. [See the comments after Theorem 4 about convergence at the endpoint of an interval. An example is = (−1)(4).] 30. We are given that the power series ∞ =0 is convergent for = −4 and divergent when = 6. So by Theorem 4 it converges for at least −4 ≤ 4 and diverges for at least ≥ 6 and −6. Therefore: (a) It converges when = 1; that is, is convergent. (b) It diverges when = 8; that is, 8 is divergent. (c) It converges when = −3; that is, (−3) is convergent. (d) It diverges when = −9; that is, (−9) = (−1)9 is divergent. 31. If = (!) ()!, then lim →∞ +1 = lim →∞ [( + 1)!] ()! (!) [( + 1)]! || = lim →∞ ( + )( + (−1) + 1) · · ·( + 2)( + 1) || = lim →∞(( + 1) + 1) (( + 1) + 2) · · · (( + 1) + ) || = lim →∞ + 1 + 1 lim →∞ + 1 + 2 · · · lim →∞ + 1 + || = 1 || 1 ⇔ || for convergence, and the radius of convergence is = 32. (a) Note that the four intervals in parts (a)–(d) have midpoint = 1 2( + ) and radius of convergence = 1 2( − ). We also know that the power series ∞ =0 has interval of convergence (−11). To change the radius of convergence to , we can change to . To shift the midpoint of the interval of convergence, we can replace with − . Thus, a power series whose interval of convergence is ( ) is ∞ =0 − , where = 1 2( + ) and = 1 2( − ). (b) Similar to Example 2, we know that ∞ =1 has interval of convergence [−11). By introducing the factor (−1) in , the interval of convergence changes to (−11]. Now change the midpoint and radius as in part (a) to get ∞ =1 (−1) 1 − as a power series whose interval of convergence is ( ]. (c) As in part (b), ∞ =1 1 − is a power series whose interval of convergence is [ ). (d) If we increase the exponent on (to say, = 2), in the power series in part (c), then when = , the power series ∞ =1 1 2 − will converge by comparison to the p-series with = 2 1, and the interval of convergence will be [ ]. 33. No. If a power series is centered at , its interval of convergence is symmetric about . If a power series has an infinite radius of convergence, then its interval of convergence must be (−∞ ∞), not [0 ∞). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.8 POWER SERIES ¤ 1029 34. The partial sums of the series ∞ =0 definitely do not converge to () = 1(1 − ) for ≥ 1, since is undefined at = 1 and negative on (1 ∞), while all the partial sums are positive on this interval. The partial sums also fail to converge to for ≤ −1, since 0 () 1 on this interval, while the partial sums are either larger than 1 or less than 0. The partial sums seem to converge to on (−11). This graphical evidence is consistent with what we know about geometric series: convergence for || 1, divergence for || ≥ 1 (see Examples 2 and 7 in Section 11.2). 35. (a) If = (−1) 2+1 !( + 1)! 22+1 , then lim →∞ +1 = lim →∞ 2+3 ( + 1)!( + 2)! 22+3 · !( + 1)! 22+1 2+1 = 22 lim →∞ ( + 1)( 1 + 2) = 0 for all . So 1() converges for all and its domain is (−∞ ∞). (b), (c) The initial terms of 1() up to = 5 are 0 = 2, 1 = − 3 16, 2 = 5 384, 3 = − 7 18,432, 4 = 9 1,474,560, and 5 = − 11 176,947,200. The partial sums seem to approximate 1() well near the origin, but as || increases, we need to take a large number of terms to get a good approximation. 36. (a) () = 1 + ∞ =1 , where = 3 2 · 3 · 5 · 6 · · · · · (3 − 1)(3), so lim →∞ +1 = ||3 lim →∞ 1 (3 + 2)(3 + 3) = 0 for all , so the domain is R. (b), (c) 0 = 1 has been omitted from the graph. The partial sums seem to approximate () well near the origin, but as || increases, we need to take a large number of terms to get a good approximation. To plot , we must first define () for the CAS. Note that for ≥ 1, the denominator of is °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1030 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 2 · 3 · 5 · 6 · · · · · (3 − 1) · 3 = (3)! 1 · 4 · 7 · · · · · (3 − 2) = (3)! =1(3 − 2), so = =1(3 − 2) (3)! 3 and thus () = 1 + ∞ =1 =1(3 − 2) (3)! 3. Both Maple and Mathematica are able to plot if we define it this way, and Derive is able to produce a similar graph using a suitable partial sum of (). Derive, Maple and Mathematica all have two initially known Airy functions, called AI·SERIES(z,m) and BI·SERIES(z,m) from BESSEL.MTH in Derive and AiryAi and AiryBi in Maple and Mathematica (just Ai and Bi in older versions of Maple). However, it is very difficult to solve for in terms of the CAS’s Airy functions, although in fact () = √3AiryAi() + AiryBi() √3AiryAi(0) + AiryBi(0) . 37. 2−1 = 1 + 2 + 2 + 23 + 4 + 25 + · · · + 2−2 + 22−1 = 1(1 + 2) + 2(1 + 2) + 4(1 + 2) + · · · + 2−2(1 + 2) = (1 + 2)(1 + 2 + 4 + · · · + 2−2) = (1 + 2)1 − 2 1 − 2 [by (11.2.3) with = 2] → 1 + 2 1 − 2 as → ∞ by (11.2.4), when || 1. Also 2 = 2−1 + 2 → 1 + 2 1 − 2 since 2 → 0 for || 1. Therefore, → 1 + 2 1 − 2 since 2 and 2−1 both approach 1 + 2 1 − 2 as → ∞. Thus, the interval of convergence is (−11) and () = 1 + 2 1 − 2 . 38. 4−1 = 0 + 1 + 22 + 33 + 04 + 15 + 26 + 37 + · · · + 34−1 = 0 + 1 + 22 + 33 1 + 4 + 8 + · · · + 4−4 → 0 + 11+−242 + 33 as → ∞ [by (11.2.4) with = 4] for 4 1 ⇔ || 1. Also 4, 4+1, 4+2 have the same limits (for example, 4 = 4−1 + 04and 4 → 0 for || 1). So if at least one of 0, 1, 2, and 3 is nonzero, then the interval of convergence is (−11) and () = 0 + 1 + 22 + 33 1 − 4 . 39. We use the Root Test on the series . We need lim →∞ || = || lim →∞ || = || 1 for convergence, or || 1, so = 1. 40. Suppose 6= 0. Applying the Ratio Test to the series ( − ), we find that = lim →∞ +1 = lim →∞ +1( − )+1 ( − ) = lim →∞ | − | |+1|(∗) = lim| − | →∞ |+1| (if lim →∞|+1| 6= 0), so the series converges when | − | lim →∞ |+1| 1 ⇔ | − | lim →∞ +1 . Thus, = lim →∞ +1 . If lim →∞ +1 = 0 and | − | 6= 0, then (∗) shows that = ∞ and so the series diverges, and hence, = 0. Thus, in all cases, = lim →∞ +1 . 41. For 2 3, diverges and converges. By Exercise 11.2.85, ( + ) diverges. Since both series converge for || 2, the radius of convergence of ( + ) is 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.9 REPRESENTATIONS OF FUNCTIONS AS POWER SERIES ¤ 1031 42. Since converges whenever || , 2 = 2 converges whenever 2 ⇔ || √, so the second series has radius of convergence √. 11.9 Representations of Functions as Power Series 1. If () = ∞ =0 has radius of convergence 10, then 0() = ∞ =1 −1 also has radius of convergence 10 by Theorem 2. 2. If () = ∞ =0 converges on (−22), then () = + ∞ =0 + 1 +1 has the same radius of convergence (by Theorem 2), but may not have the same interval of convergence—it may happen that the integrated series converges at an endpoint (or both endpoints). 3. Our goal is to write the function in the form 1 1 − , and then use Equation (1) to represent the function as a sum of a power series. () = 1 1 + = 1 1 − (−) = ∞ =0 (−) = ∞ =0 (−1) with |−| 1 ⇔ || 1, so = 1 and = (−11). 4. () = 5 1 − 42 = 51 −142 = 5 ∞=0(42) = 5 ∞=042. The series converges when 42 1 ⇔ ||2 1 4 ⇔ || 1 2, so = 1 2 and = − 1 2 1 2. 5. () = 2 3 − = 2 3 1 −13 = 23 ∞=0 3 or, equivalently, 2 ∞=0 31+1 . The series converges when 3 1, that is, when || 3, so = 3 and = (−33). 6. () = 4 2 + 3 = 4 3 1 + 2 13 = 431 − (−123) = 4 3 ∞=0 −23 or, equivalently, ∞=0(−1) 2 3 +2 +1 . The series converges when − 2 3 1, that is, when || 3 2, so = 3 2 and = − 3 2 3 2. 7. () = 2 4 + 16 = 2 161 + 1416 = 162 1 − [−1(2)]4 = 162 ∞=0 −24 or, equivalently, ∞=0 (−1) 24+4 4+2 . The series converges when −24 1 ⇒ 2 1 ⇒ || 2, so = 2 and = (−22). 8. () = 22 + 1 = 1 − (−1 22) = ∞=0(−22) or, equivalently, ∞=0(−1)22+1. The series converges when −22 1 ⇒ 2 1 2 ⇒ || √12, so = √12 and = −√12 √12. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1032 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 9. () = − 1 + 2 = + 2 − 3 + 2 = 1 − 3 + 2 = 1 − 32 2 + 1 = 1 − 3 2 · 1 − (−1 2) = 1 − 3 2 ∞ =0 −2 = 1 − 3 2 − 3 2 ∞=1 −2 = −12 − ∞=1 (−1) 2+13 . The geometric series ∞ =0 −2 converges when −2 1 ⇔ || 2, so = 2 and = (−22). Alternatively, you could write () = 1 − 3 + 2 1 and use the series for + 2 1 found in Example 2. 10. () = 2 + 2 [ 0] = 2 1 − (−122) = 1 ∞=0 −22 = ∞=0 (−1) 2+1 2 . The geometric series ∞ =0 −22 converges when −22 1 ⇔ || , so = and = (− ). 11. () = 2 − 4 2 − 4 + 3 = 2 − 4 ( − 1)( − 3) = − 1 + − 3 ⇒ 2 − 4 = ( − 3) + ( − 1). Let = 1 to get −2 = −2 ⇔ = 1 and = 3 to get 2 = 2 ⇔ = 1. Thus, 2 − 4 2 − 4 + 3 = 1 − 1 + 1 − 3 = −1 1 − + 1 − 3 1 − (13) = − ∞=0 − 13 ∞=0 3 = ∞=0 −1 − 31+1 . We represented as the sum of two geometric series; the first converges for ∈ (−11) and the second converges for ∈ (−33). Thus, the sum converges for ∈ (−11) = 12. () = 2 + 3 2 + 3 + 2= 2 + 3 ( + 1)( + 2) = + 1 + + 2 ⇒ 2 + 3 = ( + 2) + ( + 1). Let = −1 to get 1 = and = −2 to get −1 = − ⇔ = 1. Thus, 2 + 3 2 + 3 + 2 = 1 + 1 + 1 + 2 = 1 1 − (−) + 1 2 1 − (−1 2) = ∞ =0 (−) + 1 2 ∞ =0 −2 = ∞=0 (−1)1 + 21+1 We represented as the sum of two geometric series; the first converges for ∈ (−11) and the second converges for ∈ (−22). Thus, the sum converges for ∈ (−11) = 13. (a) () = 1 (1 + )2 = 1 + −1 = − ∞=0(−1) [from Exercise 3] = ∞ =1 (−1)+1−1 [from Theorem 2(i)] = ∞ =0 (−1)( + 1) with = 1. In the last step, note that we decreased the initial value of the summation variable by 1, and then increased each occurrence of in the term by 1 [also note that (−1)+2 = (−1)]. (b) () = 1 (1 + )3 = − 1 2 (1 +1)2 = −1 2 ∞=0(−1)( + 1) [from part (a)] = − 1 2 ∞ =1 (−1)( + 1)−1 = 1 2 ∞ =0 (−1)( + 2)( + 1) with = 1. (c) () = 2 (1 + )3 = 2 · (1 +1)3 = 2 · 1 2 ∞=0(−1)( + 2)( + 1) [from part (b)] = 1 2 ∞ =0 (−1)( + 2)( + 1)+2 [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.9 REPRESENTATIONS OF FUNCTIONS AS POWER SERIES ¤ 1033 To write the power series with rather than +2, we will decrease each occurrence of in the term by 2 and increase the initial value of the summation variable by 2. This gives us 1 2 ∞ =2 (−1)()( − 1) with = 1. 14. (a) 1 −1 = −ln(1 − ) + and 1 −1 = (1 + + 2 + · · ·) = + 22 + 33 + · · · + = ∞=1 + for || 1. So −ln(1 − ) = ∞ =1 + and letting = 0 gives 0 = . Thus, () = ln(1 − ) = − ∞ =1 with = 1. (b) () = ln(1 − ) = − ∞ =1 = − ∞ =1 +1 . (c) Letting = 1 2 gives ln 1 2 = − ∞ =1 (12) ⇒ ln 1 − ln 2 = − ∞ =1 1 2 ⇒ ln 2 = ∞ =1 1 2 . 15. () = ln(5 − ) = − 5 − = −15 1 −5 = −15 ∞=05 = − 1 5 ∞=0 5(+1 + 1) = − ∞=1 5 Putting = 0, we get = ln 5. The series converges for |5| 1 ⇔ || 5, so = 5. 16. () = 2 tan−1(3) = 2 ∞ =0 (−1) (3)2+1 2 + 1 [by Example 7] = ∞ =0 (−1) 6+3+2 2 + 1 = ∞ =0 (−1) 6+5 2 + 1 for 3 1 ⇔ || 1, so = 1. 17. We know that 1 1 + 4 = 1 1 − (−4) = ∞ =0 (−4). Differentiating, we get −4 (1 + 4)2 = ∞ =1 (−4)−1 = ∞ =0 (−4)+1( + 1), so () = (1 + 4)2 = − 4 · −4 (1 + 4)2 = − 4 ∞ =0 (−4)+1( + 1) = ∞ =0 (−1)4( + 1)+1 for |−4| 1 ⇔ || 1 4, so = 1 4. 18. 1 2 − = 1 2(1 − 2) = 1 2 ∞ =0 2 = ∞=0 21+1 . Now 2 −1 = ∞=0 21+1 ⇒ 1 (2 − )2 = ∞ =1 1 2+1 −1 and (2 −1)2 = ∞=1 21+1 −1 ⇒ 2 (2 − )3 = ∞ =2 1 2+1 ( − 1)−2 = ∞ =0 ( + 2)( + 1) 2+3 . Thus, () = 2 − 3 = (2 −3)3 = 23 · (2 −2)3 = 23 ∞=0 ( + 2)( 2+3 + 1) = ∞=0 ( + 2)( 2+4 + 1)+3 for 2 1 ⇔ || 2, so = 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1034 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 19. By Example 5, 1 (1 − )2 = ∞ =0 ( + 1). Thus, () = 1 + (1 − )2 = 1 (1 − )2 + (1 − )2 = ∞ =0 ( + 1) + ∞ =0 ( + 1)+1 = ∞ =0 ( + 1) + ∞ =1 [make the starting values equal] = 1 + ∞ =1 [( + 1) + ] = 1 + ∞ =1 (2 + 1) = ∞ =0 (2 + 1) with = 1. 20. By Example 5, 1 (1 − )2 = ∞ =0 ( + 1), so (1 −1)2 = ∞=0( + 1) ⇒ (1 −2)3 = ∞=1( + 1)−1. Thus, () = 2 + (1 − )3 = 2 (1 − )3 + (1 − )3 = 2 2 · 2 (1 − )3 + 2 · 2 (1 − )3 = 2 2 ∞ =1 ( + 1)−1 + 2 ∞ =1 ( + 1)−1 = ∞ =1 ( + 1) 2 +1 + ∞ =1 ( + 1) 2 = ∞ =2 ( − 1) 2 + ∞ =1 ( + 1) 2 [make the exponents on equal by changing an index] = ∞ =2 2 − 2 + + ∞ =2 2 + 2 [make the starting values equal] = + ∞ =2 2 = ∞ =1 2 with = 1 21. () = 2 2 + 1 = 21 − (1−2) = 2 ∞=0(−2) = ∞=0(−1) 2+2. This series converges when −2 1 ⇔ 2 1 ⇔ || 1, so = 1. The partial sums are 1 = 2, 2 = 1 − 4, 3 = 2 + 6, 4 = 3 − 8, 5 = 4 + 10, . Note that 1 corresponds to the first term of the infinite sum, regardless of the value of the summation variable and the value of the exponent. As increases, () approximates better on the interval of convergence, which is (−11). 22. From Example 6, we have ln(1 + ) = ∞ =1 (−1)−1 with || 1, so() = ln(1 + 4) = ∞ =1 (−1)−1 4 with 4 1 ⇔ || 1 [ = 1]. The partial sums are 1 = 4, 2 = 1 − 1 28, 3 = 2 + 1 312, 4 = 3 − 1 416, 5 = 4 + 1 520, . Note that 1 corresponds to the first term of the infinite sum, regardless of the value of the summation variable and the value of the exponent. As increases, () approximates better on the interval of convergence, which is [−11]. (When = ±1, the series is the convergent alternating harmonic series.) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.9 REPRESENTATIONS OF FUNCTIONS AS POWER SERIES ¤ 1035 23. () = ln1 + 1 − = ln(1 + ) − ln(1 − ) = 1 + + 1 − = 1 − (−) + 1 − = ∞=0(−1) + ∞=0 = [(1 − + 2 − 3 + 4 − · · ·) + (1 + + 2 + 3 + 4 + · · ·)] = (2 + 22 + 24 + · · ·) = ∞=0 22 = + ∞=0 222+ 1 +1 But (0) = ln 1 1 = 0, so = 0 and we have () = ∞ =0 22+1 2 + 1 with = 1. If = ±1, then () = ±2 ∞ =0 1 2 + 1, which both diverge by the Limit Comparison Test with = 1 . The partial sums are 1 = 2 1 , 2 = 1 + 23 3 , 3 = 2 + 25 5 , . As increases, () approximates better on the interval of convergence, which is (−11). 24. () = tan−1(2) = 2 1 + 4 2 = 2 ∞=0(−1) 42 = 2 ∞=0(−1)42 = + 2 ∞ =0 (−1)42+1 2 + 1 = ∞ =0 (−1)22+12+1 2 + 1 [(0) = tan−1 0 = 0, so = 0] The series converges when 42 1 ⇔ || 1 2, so = 1 2. If = ± 1 2, then () = ∞ =0 (−1) 1 2 + 1 and () = ∞ =0 (−1)+1 1 2 + 1 , respectively. Both series converge by the Alternating Series Test. The partial sums are 1 = 2 1 , 2 = 1 − 233 3 , 3 = 2 + 255 5 , . As increases, () approximates better on the interval of convergence, which is − 1 2 1 2. 25. 1 − 8 = · 1 1 − 8 = ∞ =0 (8) = ∞ =0 8+1 ⇒ 1 − 8 = + ∞=0 88+ 2 +2 . The series for 1 −1 8 converges when 8 1 ⇔ || 1, so = 1 for that series and also the series for (1 − 8). By Theorem 2, the series for 1 − 8 also has = 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1036 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 26. 1 + 3 = · 1 1 − (−3) = ∞ =0 (−3) = ∞ =0 (−1)3+1 ⇒ 1 + 3 = + ∞=0(−1) 33+ 2 +2 . The series for 1 1 + 3 converges when −3 1 ⇔ || 1, so = 1 for that series and also for the series 1 + 3 . By Theorem 2, the series for 1 + 3 also has = 1. 27. From Example 6, ln(1 + ) = ∞ =1 (−1)−1 for || 1, so 2 ln(1 + ) = ∞ =1 (−1)−1 +2 and 2 ln(1 + ) = + ∞=1(−1)−1 (+ 3) +3 . = 1 for the series for ln(1 + ), so = 1 for the series representing 2 ln(1 + ) as well. By Theorem 2, the series for 2 ln(1 + ) also has = 1. 28. From Example 7, tan−1 = ∞ =0 (−1) 2+1 2 + 1 for || 1, so tan−1 = ∞ =0 (−1) 2 2 + 1 and tan−1 = + ∞=0(−1) (22+ 1) +1 2 . = 1 for the series for tan−1 , so = 1 for the series representing tan−1 as well. By Theorem 2, the series for tan−1 also has = 1. 29. 1 + 3 = 1 − (1−3) = ∞=0(−3) = ∞=0(−1)3+1 ⇒ 1 +3 = ∞=0(−1)3+1 = + ∞=0(−1) 33+ 2 +2 . Thus, = 003 1 +3 = 22 − 55 + 88 − 11 11 + · · · 0 03 = (023)2 − (053)5 + (083)8 − (011 3)11 + · · · . The series is alternating, so if we use the first three terms, the error is at most (03)1111 ≈ 16 × 10−7. So ≈ (03)22 − (03)55 + (03)88 ≈ 0044 522 to six decimal places. 30. We substitute 2 for in Example 7, and find that arctan(2) = ∞=0(−1) ( 22)+ 1 2+1 = ∞=0(−1) 22+1 2(2 +1 + 1) = + ∞ =0 (−1) 2+2 22+1(2 + 1)(2 + 2) Thus, = 012 arctan(2) = 2(1)(2) 2 − 23(3)(4) 4 + 25(5)(6) 6 − 27(7)(8) 8 + 29(9)(10) 10 − · · · 1 02 = 1 23(1)(2) − 1 27(3)(4) + 1 211(5)(6) − 1 215(7)(8) + 1 219(9)(10) − · · · [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.9 REPRESENTATIONS OF FUNCTIONS AS POWER SERIES ¤ 1037 The series is alternating, so if we use four terms, the error is at most 1(219 · 90) ≈ 21 × 10−8. So ≈ 1 16 − 1 1536 + 1 61,440 − 1 1,835,008 ≈ 0061 865 to six decimal places. Remark: The sum of the first three terms gives us the same answer to six decimal places, but the error is at most 11,835,008 ≈ 55 × 10−7, slightly too large to guarantee the desired accuracy. 31. We substitute 2 for in Example 6, and find that ln(1 + 2) = ∞=1(−1)−1 (2) = ∞=1(−1)−1 2+1 = + ∞=1(−1)−1 (2 2+2 + 2) Thus, ≈ 002 ln(1 + 2) = 1(4) 4 − 2(6) 6 + 3(8) 8 − 4(10) 10 + · · · 0 02 = (042)4 − (012 2)6 + (024 2)8 − (040 2)10 + · · · The series is alternating, so if we use two terms, the error is at most (02)824 ≈ 11 × 10−7. So ≈ (02)4 4 − (02)6 12 ≈ 0000 395 to six decimal places. 32. 003 1 +24 = 003 2 ∞=0(−1)4 = ∞=0 (−41) + 3 4+3 0 03 = ∞=0 (4(−+ 3)10 1) 344+3 +3 = 33 3 × 103 − 37 7 × 107 + 311 11 × 1011 − · · · The series is alternating, so if we use only two terms, the error is at most 311 11 × 1011 ≈ 0000 000 16. So, to six decimal places, 003 1 +24 ≈ 3 ×33103 − 7 ×37107 ≈ 0008 969. 33. By Example 7, arctan = − 3 3 + 5 5 − 7 7 + · · · , so arctan 02 = 02 − (032)3 + (052)5 − (072)7 + · · · . The series is alternating, so if we use three terms, the error is at most (02)7 7 ≈ 0000 002. Thus, to five decimal places, arctan 02 ≈ 02 − (02)3 3 + (02)5 5 ≈ 0197 40. 34. () = ∞ =0 (−1)2 (2)! ⇒ 0() = ∞ =1 (−1)22−1 (2)! [the first term disappears], so 00() = ∞ =1 (−1)(2)(2 − 1)2−2 (2)! = ∞ =1 (−1)2(−1) [2( − 1)]! = ∞ =0 (−1)+12 (2)! [substituting + 1 for ] = − ∞ =0 (−1)2 (2)! = −() ⇒ 00() + () = 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1038 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 35. (a) 0() = ∞ =0 (−1) 2 22(!)2 00() = ∞ =1 (−1) 22−1 22(!)2 , and 000() = ∞ =1 (−1) 2(2 − 1)2−2 22(!)2 , so 2000() + 00() + 20() = ∞ =1 (−1) 2(2 − 1)2 22(!)2 + ∞ =1 (−1) 22 22(!)2 + ∞ =0 (−1) 2+2 22(!)2 = ∞ =1 (−1) 2(2 − 1)2 22(!)2 + ∞ =1 (−1) 22 22(!)2 + ∞ =1 (−1)−1 2 22−2 [( − 1)!]2 = ∞ =1 (−1) 2(2 − 1)2 22(!)2 + ∞ =1 (−1) 22 22(!)2 + ∞ =1 (−1)(−1)−12222 22(!)2 = ∞ =1 (−1) 2(2 −21) + 2 2(!)2 − 222 2 = ∞ =1 (−1) 42 −222+ 2 (!)2 − 42 2 = 0 (b) 01 0() = 01 ∞=0 (2−21) (!)22 = 011 − 42 + 644 − 2304 6 + · · · = − 3·34 + 5· 564 − 7 ·2304 7 + · · · 1 0 = 1 − 12 1 + 320 1 − 16,1128 + · · · Since 1 16,128 ≈ 0000062, it follows from The Alternating Series Estimation Theorem that, correct to three decimal places, 01 0() ≈ 1 − 12 1 + 320 1 ≈ 0920. 36. (a) 1() = ∞ =0 (−1)2+1 ! ( + 1)! 22+1 , 10 () = ∞ =0 (−1) (2 + 1)2 !( + 1)! 22+1 , and 100() = ∞ =1 (−1) (2 + 1) (2)2−1 !( + 1)! 22+1 . 2100() + 10() + 2 − 11() = ∞ =1 (−1) (2 + 1)(2)2+1 ! ( + 1)! 22+1 + ∞ =0 (−1) (2 + 1)2+1 ! ( + 1)! 22+1 + ∞ =0 (−1) 2+3 !( + 1)! 22+1 − ∞ =0 (−1) 2+1 !( + 1)! 22+1 = ∞ =1 (−1) (2 + 1)(2)2+1 ! ( + 1)! 22+1 + ∞ =0 (−1) (2 + 1)2+1 ! ( + 1)! 22+1 − ∞ =1 (−1) 2+1 ( − 1)!!22−1 − ∞ =0 (−1) 2+1 ! ( + 1)! 22+1 Replace in the third term with − 1 = 2 − 2 + ∞ =1 (−1)(2 + 1)(2) + (2 !(+ 1)! 2 + 1) −2(+1 )( + 1)22 − 12+1 = 0 (b) 0() = ∞ =0 (−1) 2 22 (!)2 ⇒ 00() = ∞ =1 (−1) (2)2−1 22 (!)2 = ∞ =0 (−1)+1 2( + 1)2+1 22+2 [( + 1)!]2 [Replace with + 1] = − ∞ =0 (−1) 2+1 22+1( + 1)!! [cancel 2 and + 1; take −1 outside sum] = −1() °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.9 REPRESENTATIONS OF FUNCTIONS AS POWER SERIES ¤ 1039 37. (a) () = ∞ =0 ! ⇒ 0() = ∞ =1 −1 ! = ∞ =1 −1 ( − 1)! = ∞ =0 ! = () (b) By Theorem 9.4.2, the only solution to the differential equation () = () is () = , but (0) = 1, so = 1 and () = . Or: We could solve the equation () = () as a separable differential equation. 38. |sin| 2 ≤ 12 , so ∞ =1 sin 2 converges by the Comparison Test. sin2 = cos, so when = 2 [ an integer], ∞ =1 0 () = ∞ =1 cos(2) = ∞ =1 1 , which diverges [harmonic series]. 00() = −sin, so ∞ =1 00() = − ∞ =1 sin, which converges only if sin = 0, or = [ an integer]. 39. If = 2 , then by the Ratio Test, lim →∞ +1 = lim →∞ +1 ( + 1)2 · 2 = || lim →∞ + 1 2 = || 1 for convergence, so = 1. When = ±1, ∞ =1 2 = ∞ =1 1 2 which is a convergent -series ( = 2 1), so the interval of convergence for is [−11]. By Theorem 2, the radii of convergence of 0 and 00 are both 1, so we need only check the endpoints. () = ∞ =1 2 ⇒ 0() = ∞ =1 −1 2 = ∞ =0 + 1 , and this series diverges for = 1 (harmonic series) and converges for = −1 (Alternating Series Test), so the interval of convergence is [−1 1). 00() = ∞ =1 −1 + 1 diverges at both 1 and −1 (Test for Divergence) since lim →∞ + 1 = 1 6= 0, so its interval of convergence is (−11). 40. (a) ∞ =1 −1 = ∞ =0 = ∞=0 = 1 −1 = −(1 −1)2 (−1) = (1 −1)2 , || 1. (b) (i) ∞ =1 = ∞ =1 −1 = (1 −1)2 [from part (a)] = (1 −)2 for || 1. (ii) Put = 1 2 in (i): ∞ =1 2 = ∞ =1 1 2 = 12 (1 − 12)2 = 2. (c) (i) ∞ =2 ( − 1) = 2 ∞ =2 ( − 1)−2 = 2 ∞=1 −1 = 2 (1 −1)2 = 2 2 (1 − )3 = 22 (1 − )3 for || 1. (ii) Put = 1 2 in (i): ∞ =2 2 − 2 = ∞ =2 ( − 1) 1 2 = 2(12)2 (1 − 12)3 = 4. (iii) From (b)(ii) and (c)(ii), we have ∞ =1 2 2 = ∞ =1 2 − 2 + ∞ =1 2 = 4 + 2 = 6. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1040 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 41. By Example 7, tan−1 = ∞ =0 (−1) 2+1 2 + 1 for || 1. In particular, for = √13, we have 6 = tan−1√13 = ∞=0(−1) 12√3+ 1 2+1 = ∞=0(−1) 1 3 √13 21+ 1, so = 6 √3 ∞ =0 (−1) (2 + 1)3 = 2√3 ∞ =0 (−1) (2 + 1)3 . 42. (a) 012 2 − + 1 = 012 ( − 1 2)2 + 34 − 12 = √23 , = √23 − 12 , = √23 = −01√3 (3√4)( 322+ 1) = 2√33tan−1 0 −1√3 = √230 − −6 = 3√ 3 (b) 1 3 + 1 = 1 ( + 1)(2 − + 1) ⇒ 1 2 − + 1 = ( + 1)1 +13 = ( + 1)1 − (1−3) = ( + 1) ∞=0(−1)3 = ∞ =0 (−1)3+1 + ∞ =0 (−1)3 for || 1 ⇒ 2 − + 1 = + ∞=0(−1) 33+ 2 +2 + ∞=0(−1) 33+ 1 +1 for || 1 ⇒ 012 2 − + 1 = ∞=0(−1) 4 · 8(31 + 2) + 2 · 8(31 + 1) = 14 ∞=0 (−81) 32+ 1 + 31+ 2. By part (a), this equals 3√3, so = 3√3 4 ∞ =0 (−1) 8 32+ 1 + 31+ 2. 11.10 Taylor and Maclaurin Series 1. Using Theorem 5 with ∞ =0 ( − 5), = ()() ! , so 8 = (8) 8!(5). 2. (a) Using Equation 6, a power series expansion of at 1 must have the form (1) + 0(1)( − 1) + · · · . Comparing to the given series, 16 − 08( − 1) + · · · , we must have 0(1) = −08. But from the graph, 0(1) is positive. Hence, the given series is not the Taylor series of centered at 1. (b) A power series expansion of at 2 must have the form (2) + 0(2)( − 2) + 1 2 00(2)( − 2)2 + · · · . Comparing to the given series, 28 + 05( − 2) + 15( − 2)2 − 01( − 2)3 + · · · , we must have 1 2 00(2) = 15; that is, 00(2) is positive. But from the graph, is concave downward near = 2, so 00(2) must be negative. Hence, the given series is not the Taylor series of centered at 2. 3. Since ()(0) = ( + 1)!, Equation 7 gives the Maclaurin series ∞ =0 ()(0) ! = ∞ =0 ( + 1)! ! = ∞ =0 ( + 1). Applying the Ratio Test with = ( + 1) gives us °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.10 TAYLOR AND MACLAURIN SERIES ¤ 1041 lim →∞ +1 = lim →∞ ( + 2)+1 ( + 1) = || lim →∞ + 2 + 1 = || · 1 = ||. For convergence, we must have || 1, so the radius of convergence = 1. 4. Since ()(4) = (−1) ! 3( + 1), Equation 6 gives the Taylor series ∞ =0 ()(4) ! ( − 4) = ∞ =0 (−1) ! 3( + 1)!( − 4) = ∞ =0 (−1) 3( + 1)( − 4), which is the Taylor series for centered at 4. Apply the Ratio Test to find the radius of convergence . lim →∞ +1 = lim →∞ (−1)+1( − 4)+1 3+1( + 2) · 3( + 1) (−1)( − 4) = lim →∞ (−1)( − 4)( + 1) 3( + 2) = 1 3 | − 4| lim →∞ + 1 + 2 = 1 3 | − 4| For convergence, 1 3 | − 4| 1 ⇔ | − 4| 3, so = 3. 5. ()() ()(0) 0 0 1 ( + 1) 1 2 ( + 2) 2 3 ( + 3) 3 4 ( + 4) 4 Using Equation 6 with = 0 to 4 and = 0, we get 4 =0 ()(0) ! ( − 0) = 0! 0 0 + 1! 1 1 + 2! 2 2 + 3! 3 3 + 4! 4 4 = + 2 + 1 23 + 1 64 6. ()() ()(2) 0 1 1 + 1 3 1 − 1 (1 + )2 − 1 9 2 2 (1 + )3 2 27 3 − 6 (1 + )4 − 6 81 3 =0 ()(2) ! ( − 2) = 1 3 0! ( − 2)0 − 1 9 1! ( − 2)1 + 2 27 2! ( − 2)2 − 6 81 3! ( − 2)3 = 1 3 − 1 9 ( − 2) + 27 1 ( − 2)2 − 81 1 ( − 2)3 7. ()() ()(8) 0 √3 2 1 1 323 1 12 2 − 2 953 − 2 288 3 10 2783 10 6912 3 =0 ()(8) ! ( − 8) = 0! 2 ( − 8)0 + 12 1! 1 ( − 8)1 − 2 288 2! ( − 8)2 + 10 6912 3! ( − 8)3 = 2 + 1 12( − 8) − 288 1 ( − 8)2 + 20,5736( − 8)3 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1042 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 8. ()() ()(1) 0 ln 0 1 1 1 2 −12 −1 3 23 2 4 −64 −6 4 =0 ()(1) ! ( − 1) = 0! 0 ( − 1)0 + 1! 1 ( − 1)1 − 2! 1 ( − 1)2 + 2 3! ( − 1)3 − 4! 6 ( − 1)4 = ( − 1) − 1 2( − 1)2 + 1 3( − 1)3 − 1 4( − 1)4 9. ()() ()(6) 0 sin 12 1 cos √32 2 −sin −12 3 −cos −√32 3 =0 ()(6) ! − 6 = 10! 2 − 6 0 + √1! 32 − 6 1 − 12! 2 − 6 2 − √3! 32 − 6 3 = 1 2 + √3 2 − 6 − 14 − 6 2 − √123 − 6 3 10. ()() ()(0) 0 cos2 1 1 −2cos sin = −sin 2 0 2 −2cos 2 −2 3 4sin 2 0 4 8cos 2 8 5 −16 sin 2 0 6 −32 cos 2 −32 6 =0 ()(0) ! ( − 0) = 0! 1 0 − 2! 2 2 + 4! 8 4 − 32 6! 6 = 1 − 2 + 1 34 − 45 2 6 11. ()() ()(0) 0 (1 − )−2 1 1 2(1 − )−3 2 2 6(1 − )−4 6 3 24(1 − )−5 24 4 120(1 − )−6 120 ... ... ... (1 − )−2 = (0) + 0(0) + 00(0) 2! 2 + 000 3! (0)3 + (4) 4!(0)4 + · · · = 1 + 2 + 6 22 + 24 6 3 + 120 24 4 + · · · = 1 + 2 + 32 + 43 + 54 + · · · = ∞ =0 ( + 1) lim →∞ +1 = lim →∞ ( + 2)+1 ( + 1) = || lim →∞ + 2 + 1 = || (1) = || 1 for convergence, so = 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.10 TAYLOR AND MACLAURIN SERIES ¤ 1043 12. ()() ()(0) 0 ln(1 + ) 0 1 (1 + )−1 1 2 −(1 + )−2 −1 3 2(1 + )−3 2 4 −6(1 + )−4 −6 5 24(1 + )−5 24 ... ... ... ln(1 + ) = (0) + 0(0) + 00(0) 2! 2 + 000(0) 3! 3 + (4) 4!(0)4 + (5) 5!(0)5 + · · · = 0 + − 1 22 + 2 63 − 24 6 4 + 120 24 5 − · · · = − 2 2 + 3 3 − 4 4 + 5 5 − · · · = ∞ =1 (−1)−1 lim →∞ +1 = lim →∞ +1 + 1 · = lim →∞ || 1 + 1 = || 1 for convergence, so = 1. Notice that the answer agrees with the entry for ln(1 + ) in Table 1, but we obtained it by a different method. (Compare with Example 11.9.6.) 13. ()() ()(0) 0 cos 1 1 −sin 0 2 −cos −1 3 sin 0 4 cos 1 ... ... ... cos = (0) + 0(0) + 00(0) 2! 2 + 000 3! (0) 3 + (4) 4!(0) 4 + · · · = 1 − 1 2! 2 + 4! 1 4 − · · · = ∞ =0 (−1) 2 (2)! [Equal to (16).] lim →∞ +1 = lim →∞ 2+2 (2 + 2)! · (2)! 2 = lim →∞ 2 (2 + 2)(2 + 1) = 0 1 for all , so = ∞. 14. ()() ()(0) 0 −2 1 1 −2−2 −2 2 4−2 4 3 −8−2 −8 4 16−2 16 ... ... ... −2 = ∞ =0 ()(0) ! = ∞ =0 (−2) ! . lim →∞ +1 = lim →∞ (−2)+1+1 ( + 1)! · ! (−2) = lim →∞ 2|| + 1 = 0 1 for all , so = ∞ 15. ()() ()(0) 0 2 1 1 2(ln 2) ln 2 2 2(ln 2)2 (ln 2)2 3 2(ln 2)3 (ln 2)3 4 2(ln 2)4 (ln 2)4 ... ... ... 2 = ∞ =0 ()(0) ! = ∞ =0 (ln 2) ! . lim →∞ +1 = lim →∞ (ln 2)+1+1 ( + 1)! · ! (ln 2) = lim →∞ (ln 2)|| + 1 = 0 1 for all , so = ∞. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1044 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 16. ()() ()(0) 0 cos 0 1 −sin + cos 1 2 −cos − 2sin 0 3 sin − 3cos −3 4 cos + 4 sin 0 5 −sin + 5 cos 5 6 −cos − 6sin 0 7 sin − 7cos −7 ... ... ... cos = (0) + 0(0) + 00(0) 2! 2 + 000 3! (0) 3 + (4) 4!(0) 4 + · · · = 0 + 1 + 0 − 3 3! 3 + 0 + 5! 5 5 + 0 − 7! 7 7 + · · · = − 1 2! 3 + 4! 1 5 − 6! 1 7 + · · · = ∞ =0 (−1) 1 (2)! 2+1 lim →∞ +1 = lim →∞ (−1)+12+3 (2 + 2)! · (2)! (−1)2+1 = lim →∞ 2 (2 + 2)(2 + 1) = 0 1 for all , so = ∞. 17. ()() ()(0) 0 sinh 0 1 cosh 1 2 sinh 0 3 cosh 1 4 sinh 0 ... ... ... ()(0) = 0 1 if if is even is odd so sinh = ∞=0 (22+ 1)! +1 . Use the Ratio Test to find . If = 2+1 (2 + 1)!, then lim →∞ +1 = lim →∞ 2+3 (2 + 3)! · (2 + 1)! 2+1 = 2 · lim →∞ 1 (2 + 3)(2 + 2) = 0 1 for all , so = ∞. 18. ()() ()(0) 0 cosh 1 1 sinh 0 2 cosh 1 3 sinh 0 ... ... ... ()(0) = 1 0 if if is even is odd so cosh = ∞=0 (2 2 )!. Use the Ratio Test to find . If = 2 (2)!, then lim →∞ +1 = lim →∞ 2+2 (2 + 2)! · (2)! 2 = 2 · lim →∞ 1 (2 + 2)(2 + 1) = 0 1 for all , so = ∞ 19. ()() ()(2) 0 5 + 23 + 50 1 54 + 62 + 1 105 2 203 + 12 184 3 602 + 12 252 4 120 240 5 120 120 6 0 0 7 0 0 ... ... ... ()() = 0 for ≥ 6, so has a finite expansion about = 2. () = 5 + 23 + = 5 =0 ()(2) ! ( − 2) = 50 0! ( − 2)0 + 105 1! ( − 2)1 + 184 2! ( − 2)2 + 252 3! ( − 2)3 + 240 4! ( − 2)4 + 120 5! ( − 2)5 = 50 + 105( − 2) + 92( − 2)2 + 42( − 2)3 + 10( − 2)4 + ( − 2)5 A finite series converges for all so = ∞ °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.10 TAYLOR AND MACLAURIN SERIES ¤ 1045 20. ()() ()(−2) 0 6 − 4 + 2 50 1 65 − 43 −160 2 304 − 122 432 3 1203 − 24 −912 4 3602 − 24 1416 5 720 −1440 6 720 720 7 0 0 8 0 0 ... ... ... ()() = 0 for ≥ 7, so has a finite expansion about = −2. () = 6 − 4 + 2 = 6 =0 ()(−2) ! ( + 2) = 50 0! ( + 2)0 − 160 1! ( + 2)1 + 432 2! ( + 2)2 − 912 3! ( + 2)3 + 1416 4! ( + 2)4 − 1440 5! ( + 2)5 + 720 6! ( + 2)6 = 50 − 160( + 2) + 216( + 2)2 − 152( + 2)3 + 59( + 2)4 − 12( + 2)5 + ( + 2)6 A finite series converges for all so = ∞. 21. ()() ()(2) 0 ln ln 2 1 1 12 2 −12 −122 3 23 223 4 −64 −624 5 245 2425 ... ... ... () = ln = ∞ =0 ()(2) ! ( − 2) = ln 2 0! ( − 2)0 + 1! 2 1 1 ( − 2)1 + 2! 2 −12 ( − 2)2 + 3! 2 2 3 ( − 2)3 + −6 4! 24 ( − 2)4 + 5! 2 245 ( − 2)5 + · · · = ln 2 + ∞ =1 (−1)+1 ( − 1)! ! 2 ( − 2) = ln 2 + ∞ =1 (−1)+1 1 2 ( − 2) lim →∞ +1 = lim →∞ (−1)+2( − 2)+1 ( + 1) 2+1 · 2 (−1)+1( − 2) = lim →∞ (−1)( − 2) ( + 1)2 = lim →∞ + 1 | −2 2| = | − 2| 2 1 for convergence, so | − 2| 2 and = 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1046 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 22. ()() ()(−3) 0 1 −13 1 −12 −132 2 23 −233 3 −64 −634 4 245 −2435 ... ... ... () = 1 = ∞ =0 ()(−3) ! ( + 3) = −13 0! ( + 3)0 + −11! 32 ( + 3)1 + −22! 33 ( + 3)2 + −634 3! ( + 3)3 + −24 4!35 ( + 3)4 + · · · = ∞ =0 −!3+1 ! ( + 3) = − ∞ =0 ( + 3) 3+1 lim →∞ +1 = lim →∞ ( + 3)+1 3+2 · 3+1 ( + 3) = lim →∞ | + 3| 3 = | + 3| 3 1 for convergence, so | + 3| 3 and = 3. 23. ()() ()(3) 0 2 6 1 22 26 2 222 46 3 232 86 4 242 166 ... ... ... () = 2 = ∞ =0 ()(3) ! ( − 3) = 6 0! ( − 3)0 + 21! 6 ( − 3)1 + 42! 6 ( − 3)2 + 86 3! ( − 3)3 + 164! 6 ( − 3)4 + · · · = ∞ =0 26 ! ( − 3) lim →∞ +1 = lim →∞ 2+16( − 3)+1 ( + 1)! · ! 26( − 3) = lim →∞ 2| − 3| + 1 = 0 1 for all , so = ∞. 24. ()() ()(2) 0 cos 0 1 −sin −1 2 −cos 0 3 sin 1 4 cos 0 5 −sin −1 6 −cos 0 7 sin 1 ... ... ... () = cos = ∞ =0 ()(2) ! − 2 = −1 1! − 2 1 + 3! 1 − 2 3 + −5!1 − 2 5 + 7! 1 − 2 7 + · · · = ∞ =0 (−1)+1 (2 + 1)! − 2 2+1 lim →∞ +1 = lim →∞ (−1)+2 − 2 2+3 (2 + 3)! · (2 + 1)! (−1)+1 − 2 2+1 = lim →∞ − 2 2 (2 + 3)(2 + 2) = 0 1 for all , so = ∞. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.10 TAYLOR AND MACLAURIN SERIES ¤ 1047 25. ()() ()() 0 sin 0 1 cos −1 2 −sin 0 3 −cos 1 4 sin 0 5 cos −1 6 −sin 0 7 −cos 1 ... ... ... () = sin = ∞ =0 ()() ! ( − ) = −1 1! ( − )1 + 3! 1 ( − )3 + −5!1 ( − )5 + 7! 1 ( − )7 + · · · = ∞ =0 (−1)+1 (2 + 1)! ( − )2+1 lim →∞ +1 = lim →∞ (−1)+2 ( − )2+3 (2 + 3)! · (2 + 1)! (−1)+1 ( − )2+1 = lim →∞ ( − )2 (2 + 3)(2 + 2) = 0 1 for all , so = ∞. 26. ()() ()(16) 0 √ 4 1 1 2−12 1 2 · 1 4 2 − 1 4−32 −1 4 · 413 3 3 8−52 3 8 · 415 4 − 15 16−72 −15 16 · 417 ... ... ... () = √ = ∞ =0 ()(16) ! ( − 16) = 4 0! ( − 16)0 + 1 2 · 1 4 · 1! 1 ( − 16)1 − 1 4 · 413 · 2! 1 ( − 16)2 + 3 8 · 1 54 · 1 3!( − 16)3 − 15 16 · 417 · 4! 1 ( − 16)4 + · · · = 4 + 1 8 ( − 16) + ∞ =2 (−1)−1 1 · 3 · 5 · · · · · (2 − 3) 242−1 ! ( − 16) = 4 + 1 8 ( − 16) + ∞ =2 (−1)−1 1 · 3 · 5 · · · · · (2 − 3) 25−2 ! ( − 16) lim →∞ +1 = lim →∞ (−1) 1 · 3 · 5 · · · · · (2 − 1)( − 16)+1 25+3( + 1)! · 25−2! (−1)−1 1 · 3 · 5 · · · · · (2 − 3)( − 16) = lim →∞ (2 − 1)| − 16| 25( + 1) = | − 16| 32 lim →∞ 2 − 1 1 + 1 = | − 16| 32 · 2 = | − 16| 16 1 for convergence, so | − 16| 16 and = 16. 27. If () = cos, then (+1)() = ±sin or ±cos. In each case, (+1)() ≤ 1, so by Formula 9 with = 0 and = 1, |()| ≤ 1 ( + 1)! ||+1. Thus, |()| → 0 as → ∞ by Equation 10. So lim →∞() = 0 and, by Theorem 8, the series in Exercise 13 represents cos for all 28. If () = sin, then (+1)() = ±sin or ±cos. In each case, (+1)() ≤ 1, so by Formula 9 with = 0 and = 1, |()| ≤ 1 ( + 1)! | − |+1. Thus, |()| → 0 as → ∞ by Equation 10. So lim →∞() → 0 and, by Theorem 8, the series in Exercise 25 represents sin for all °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1048 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 29. If () = sinh, then for all , (+1)() = cosh or sinh. Since |sinh| |cosh| = cosh for all , we have (+1)() ≤ cosh for all . If is any positive number and || ≤ , then (+1)() ≤ cosh ≤ cosh, so by Formula 9 with = 0 and = cosh, we have |()| ≤ cosh ( + 1)! ||+1. It follows that |()| → 0 as → ∞ for || ≤ (by Equation 10). But was an arbitrary positive number. So by Theorem 8, the series represents sinh for all . 30. If () = cosh, then for all , (+1)() = cosh or sinh. Since |sinh| |cosh| = cosh for all , we have (+1)() ≤ cosh for all . If is any positive number and || ≤ , then (+1)() ≤ cosh ≤ cosh, so by Formula 9 with = 0 and = cosh, we have |()| ≤ cosh ( + 1)! ||+1. It follows that |()| → 0 as → ∞ for || ≤ (by Equation 10). But was an arbitrary positive number. So by Theorem 8, the series represents cosh for all . 31. √4 1 − = [1 + (−)]14 = ∞ =0 14(−) = 1 + 1 4(−) + 1 4 2! − 3 4(−)2 + 1 4 − 3 43! − 7 4(−)3 + · · · = 1 − 1 4 + ∞ =2 (−1)−1(−1) · [3 · 7 · · · · · (4 − 5)] 4 · ! = 1 − 1 4 − ∞ =2 3 · 7 · · · · · (4 − 5) 4 · ! and |−| 1 ⇔ || 1, so = 1. 32. √3 8 + = 3 81 + 8 = 21 + 813 = 2 ∞=0 13 8 = 21 + 1 38 + 1 3− 2! 2 3 82 + 1 3− 2 33! − 5 3 83 + · · · = 21 + 24 1 + ∞=2 (−1)−1 ·3[2··58· · · · · · ! (3 − 4)] = 2 + 1 12 + 2 ∞ =2 (−1)−1[2 · 5 · · · · · (3 − 4)] 24 · ! and 8 1 ⇔ || 8, so = 8. 33. 1 (2 + )3 = 1 [2(1 + 2)]3 = 1 8 1 + 2−3 = 18 ∞ =0−32. The binomial coefficient is −3 = (−3)(−4)(−5) · · · · · ! (−3 − + 1) = (−3)(−4)(−5)· · · · · ! [−( + 2)] = (−1) · 2 · 3 · 4 · 5 · · · · · ( + 1)( + 2) 2 · ! = (−1)( + 1)( + 2) 2 Thus, 1 (2 + )3 = 1 8 ∞ =0 (−1)( + 1)( + 2) 2 2 = ∞ =0 (−1)( + 1)( + 2) 2+4 for 2 1 ⇔ || 2, so = 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.10 TAYLOR AND MACLAURIN SERIES ¤ 1049 34. (1 + )34 = ∞ =0 3 4 = 1 + 3 4 + 3 4−2! 1 4 2 + 3 4− 1 43! − 5 4 3 + · · · = 1 + 3 4 + ∞ =2 (−1)−1 · 3 · [1 · 5 · 9 · · · · · (4 − 7)] 4 · ! for || 1, so = 1. 35. arctan = ∞ =0 (−1) 2+1 2 + 1 , so () = arctan(2) = ∞ =0 (−1) 22+1 2 + 1 = ∞ =0 (−1) 1 2 + 1 4+2, = 1. 36. sin = ∞ =0 (−1) 2+1 (2 + 1)!, so () = sin4 = ∞=0(−1) (24+ 1)! 2+1 = ∞=0(−1) 42+1 (2 2+1+ 1)! 2+1, = ∞. 37. cos = ∞ =0 (−1) 2 (2)! ⇒ cos 2 = ∞ =0 (−1) (2)2 (2)! = ∞ =0 (−1) 222 (2)! , so () = cos 2 = ∞ =0 (−1) 22 (2)! 2+1, = ∞. 38. = ∞ =0 ! , so () = 3 − 2 = ∞ =0 (3) ! − ∞ =0 (2) ! = ∞ =0 3 ! − ∞ =0 2 ! = ∞ =0 3 − 2 ! , = ∞. 39. cos = ∞ =0 (−1) 2 (2)! ⇒ cos 1 22 = ∞ =0 (−1) 1 222 (2)! = ∞ =0 (−1) 4 22 (2)!, so () = cos 1 22 = ∞ =0 (−1) 1 22(2)! 4+1, = ∞. 40. ln(1 + ) = ∞ =1 (−1)−1 ⇒ ln(1 + 3) = ∞ =1 (−1)−1 3 , so () = 2 ln(1 + 3) = ∞ =1 (−1)−1 3+2 , = 1. 41. We must write the binomial in the form (1+ expression), so we’ll factor out a 4. √4 + 2 = 4(1 + 24) = 21 + 24 = 2 1 + 42 −12 = 2 ∞=0−1 242 = 2 1 + − 1 242 + − 1 2 2!− 3 242 2 + − 1 2−3!3 2− 5 242 3 + · · · = 2 + 2 ∞ =1 (−1) 1 · 3 · 5 · · · · · (2 − 1) 2 · 4 · ! 2 = 2 + ∞ =1 (−1) 1 · 3 · 5 · · · · · (2 − 1) !23+1 2+1 and 42 1 ⇔ |2| 1 ⇔ || 2, so = 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1050 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 42. √2 + 2 = 2(1 + 2 2) = √221 + 2−12 = √22 ∞=0−1 22 = 2 √21 + − 1 22 + − 1 2 2!− 3 222 + − 1 2−3!3 2− 5 223 + · · · = 2 √2 + 2 √2 ∞ =1 (−1) 1 · 3 · 5 · · · · · (2 − 1) !22 = 2 √2 + ∞ =1 (−1) 1 · 3 · 5 · · · · · (2 − 1) !22+12 +2 and 2 1 ⇔ || 2, so = 2. 43. sin2 = 1 2 (1 − cos 2) = 1 21 − ∞=0 (−1) (2(2)!)2 = 121 − 1 − ∞=1 (−1) (2(2)!)2 = ∞=1 (−1)+1 (222)! −12 , = ∞ 44. − sin 3 = 1 3 − ∞=0 (−(21) + 1)! 2+1 = 13 − − ∞=1 (−(21) + 1)! 2+1 = 13 − ∞=0 (−(2 1)+1 + 3)! 2+3 = 1 3 ∞ =0 (−1)2+3 (2 + 3)! = ∞ =0 (−1)2 (2 + 3)! and this series also gives the required value at = 0 (namely 16); = ∞. 45. cos (16) = ∞ =0 (−1) 2 (2)! ⇒ () = cos(2) = ∞ =0 (−1) (2)2 (2)! = ∞ =0 (−1)4 (2)! = 1 − 1 24 + 24 1 8 − 720 1 12 + · · · The series for cos converges for all , so the same is true of the series for (), that is, = ∞. Notice that, as increases, () becomes a better approximation to (). 46. ln(1 + ) = ∞ =1 (−1)−1 ⇒ () = ln(1 + 2) = ∞ =1 (−1)−1(2) = ∞ =1 (−1)−12 = 2 − 1 24 + 1 36 − 1 48 + · · · The series for ln(1 + ) has = 1 and 2 1 ⇔ || 1, so the series for () also has = 1. From the graphs of and the first few Taylor polynomials, we see that () provides a closer fit to () near 0 as increases. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.10 TAYLOR AND MACLAURIN SERIES ¤ 1051 47. (11) = ∞ =0 ! , so − = ∞ =0 (−) ! = ∞ =0 (−1) ! , so () = − = ∞ =0 (−1) 1 ! +1 = − 2 + 1 2 3 − 1 6 4 + 24 1 5 − 120 1 6 + · · · = ∞ =1 (−1)−1 ( − 1)! The series for converges for all , so the same is true of the series for (); that is, = ∞. From the graphs of and the first few Taylor polynomials, we see that () provides a closer fit to () near 0 as increases. 48. From Table 1, tan−1 = ∞ =0 (−1) 2+1 2 + 1 , so () = tan−1(3) = ∞ =0 (−1) (3)2+1 2 + 1 = ∞ =0 (−1) 6+3 2 + 1 = 3 − 1 3 9 + 1 5 15 − 1 7 21 + · · · The series for tan−1 has = 1 and 3 1 ⇔ || 1, so the series for () also has = 1. From the graphs of and the first few Taylor polynomials, we see that () provides a closer fit to () near 0 as increases. 49. 5◦ = 5◦ 180 ◦ = 36 radians and cos = ∞ =0 (−1) 2 (2)! = 1 − 2! 2 + 4! 4 − 6! 6 + · · · , so cos 36 = 1 − (36)2 2! + (36)4 4! − (36)6 6! + · · · . Now 1 − (2! 36)2 ≈ 099619 and adding (4! 36)4 ≈ 24 × 10−6 does not affect the fifth decimal place, so cos 5◦ ≈ 099619 by the Alternating Series Estimation Theorem. 50. 1 10 √ = −110 and = ∞ =0 ! = 1 + + 2! 2 + 3! 3 + · · · , so −110 = 1 − 1 10 + (110)2 2! − (110)3 3! + (110)4 4! − (110)5 5! + · · · . Now 1 − 1 10 + (110)2 2! − (110)3 3! + (110)4 4! ≈ 090484 and subtracting (15! 10)5 ≈ 83 × 10−8 does not affect the fifth decimal place, so −110 ≈ 090484 by the Alternating Series Estimation Theorem. 51. (a) 1√1 − 2 = 1 + −2−12 = 1 + − 1 2−2 + − 1 2 2!− 3 2−22 + − 1 2−3!3 2− 5 2−23 + · · · = 1 + ∞ =1 1 · 3 · 5 · · · · · (2 − 1) 2 · ! 2 (b) sin−1 = √1 1− 2 = + + ∞=1 1 · 3(2·5 + 1)2 · · · · · (2·−! 1)2+1 = + ∞ =1 1 · 3 · 5 · · · · · (2 − 1) (2 + 1)2 · ! 2+1 since 0 = sin−1 0 = . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1052 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 52. (a) 1√4 1 + = (1 + )−14 = ∞ =0−1 4 = 1 − 14 + − 1 4 2!− 5 42 + − 1 4−3! 5 4 − 9 43 + · · · = 1 − 1 4 + ∞ =2 (−1) 1 · 5 · 9 · · · · · (4 − 3) 4 · ! (b) 1√4 1 + = 1 − 1 4 + 32 5 2 − 128 15 3 + 2048 195 4 − · · · . 1√4 11 = 1√4 1 + 01, so let = 01. The sum of the first four terms is then 1 − 1 4(01) + 32 5 (01)2 − 128 15 (01)3 ≈ 0976. The fifth term is 2048 195 (01)4 ≈ 0000 009 5, which does not affect the third decimal place of the sum, so we have 1√4 11 ≈ 0976. (Note that the third decimal place of the sum of the first three terms is affected by the fourth term, so we need to use more than three terms for the sum.) 53. √1 + 3 = (1 + 3)12 = ∞ =0 1 2 (3) = ∞=0 1 2 3 ⇒ 1 + 3 = + ∞=0 1 2 33+ 1 +1 , with = 1. 54. sin = ∞ =0 (−1) 2+1 (2 + 1)! ⇒ sin(2) = ∞ =0 (−1) (2)2+1 (2 + 1)! = ∞ =0 (−1) 4+2 (2 + 1)! ⇒ 2 sin(2) = ∞ =0 (−1) 4+4 (2 + 1)! ⇒ 2 sin(2) = + ∞=0(−1) (2 + 1)!(4 4+5 + 5), with = ∞. 55. cos (16) = ∞ =0 (−1) 2 (2)! ⇒ cos − 1 = ∞ =1 (−1) 2 (2)! ⇒ cos − 1 = ∞ =1 (−1) 2−1 (2)! ⇒ cos− 1 = + ∞=1(−1) 2 · 2(2 )!, with = ∞. 56. arctan = ∞ =0 (−1) 2+1 2 + 1 ⇒ arctan(2) = ∞ =0 (−1) (2)2+1 2 + 1 = ∞ =0 (−1) 4+2 2 + 1 ⇒ arctan(2) = + ∞=0(−1) (2 + 1)(4 4+3 + 3), with = 1. 57. arctan = ∞ =0 (−1) 2+1 2 + 1 for || 1, so 3 arctan = ∞ =0 (−1) 2+4 2 + 1 for || 1 and 3 arctan = + ∞=0(−1) (2 + 1)(2 2+5 + 5). Since 1 2 1, we have 012 3 arctan = ∞=0(−1) (2(1 + 1)(2 2)2+5+ 5) = (11·2) 55 − (13·2) 77 + (15·2) 99 − (17·2) 1111 + · · · . Now (12)5 1 · 5 − (12)7 3 · 7 + (12)9 5 · 9 ≈ 00059 and subtracting (12)11 7 · 11 ≈ 63 × 10−6 does not affect the fourth decimal place, so 012 3 arctan ≈ 00059 by the Alternating Series Estimation Theorem. 58. sin = ∞ =0 (−1) 2+1 (2 + 1)! for all , so sin(4) = ∞ =0 (−1) 8+4 (2 + 1)! for all and sin(4) = + ∞=0(−1) (2 + 1)! (8 8+5 + 5). Thus, °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.10 TAYLOR AND MACLAURIN SERIES ¤ 1053 01 sin(4) = ∞=0(−1) (2 + 1)! (8 1 + 5) = 1!1· 5 − 3! 1 · 13 + 5! 1 · 21 − 7! 1 · 29 + · · · . Now 1 1! · 5 − 1 3! · 13 + 1 5! · 21 ≈ 01876 and subtracting 7! 1 · 29 ≈ 684 × 10−6 does not affect the fourth decimal place, so 01 sin(4) ≈ 01876 by the Alternating Series Estimation Theorem. 59. √1 + 4 = (1 + 4)12 = ∞ =0 1 2(4), so 1 + 4 = + ∞=0 1 244+ 1 +1 and hence, since 04 1, we have = 004 1 + 4 = ∞=0 1 2(044)+ 1 4+1 = (1) (04)1 0! + 1 2 1! (04)5 5 + 1 2 − 1 2 2! (04)9 9 + 1 2 − 1 2− 3 2 3! (04)13 13 + 1 2 − 1 2− 3 2− 5 2 4! (04)17 17 + · · · = 04 + (04)5 10 − (04)9 72 + (04)13 208 − 5(04)17 2176 + · · · Now (04)9 72 ≈ 36 × 10−6 5 × 10−6, so by the Alternating Series Estimation Theorem, ≈ 04 + (010 4)5 ≈ 040102 (correct to five decimal places). 60. 005 2−2 = 005 ∞=0 (−1)! 2+2 = ∞=0 (−!(2 1)+ 3) 2+3 1 02 = ∞=0 !(2(−+ 3)2 1) 2+3 and since the term with = 2 is 1 1792 0001, we use 1 =0 (−1) !(2 + 3)22+3 = 1 24 − 1 160 ≈ 00354. 61. lim →0 − ln(1 + ) 2 = lim →0 − ( − 1 22 + 1 33 − 1 44 + 1 55 − · · ·) 2 = lim →0 1 2 2 − 1 33 + 1 44 − 1 55 + · · · 2 = lim →0 ( 1 2 − 1 3 + 1 42 − 1 53 + · · ·) = 1 2 since power series are continuous functions. 62. lim →0 1 − cos 1 + − = lim →0 1 − 1 − 2! 1 2 + 4! 1 4 − 6! 1 6 + · · · 1 + − 1 + + 2! 1 2 + 3! 1 3 + 4! 1 4 + 5! 1 5 + 6! 1 6 + · · · = lim →0 1 2!2 − 4! 1 4 + 6! 1 6 − · · · − 1 2!2 − 3! 1 3 − 4! 1 4 − 5! 1 5 − 6! 1 6 − · · · = lim →0 1 2! − 1 4!2 + 6! 1 4 − · · · − 1 2! − 1 3! − 4! 1 2 − 5! 1 3 − 6! 1 4 − · · · = 1 2 − 0 − 1 2 − 0 = −1 since power series are continuous functions. 63. lim →0 sin − + 1 63 5 = lim →0 − 3! 1 3 + 5! 1 5 − 7! 1 7 + · · · − + 1 63 5 = lim →0 1 5!5 − 7! 1 7 + · · · 5 = lim →05! 1 − 7! 2 + 9! 4 − · · · = 5! 1 = 120 1 since power series are continuous functions. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1054 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 64. lim →0 √1 + − 1 − 1 2 2 = lim →0 1 + 1 2 − 1 82 + 16 1 3 − · · · − 1 − 1 2 2 = lim →0 − 1 8 2 + 1 163 − · · · 2 = lim →0 − 1 8 + 16 1 − · · · = − 1 8 since power series are continuous functions. 65. lim →0 3 − 3 + 3 tan−1 5 = lim →0 3 − 3 + 3 − 1 33 + 1 55 − 1 77 + · · · 5 = lim →0 3 − 3 + 3 − 3 + 3 55 − 3 77 + · · · 5 = lim →0 3 5 5 − 3 77 + · · · 5 = lim →0 3 5 − 3 72 + · · · = 3 5 since power series are continuous functions. 66. lim →0 tan − 3 = lim →0 + 1 33 + 15 2 5 + · · · − 3 = lim →0 1 3 3 + 2 155 + · · · 3 = lim →0 1 3 + 15 2 2 + · · · = 1 3 since power series are continuous functions. 67. From Equation 11, we have −2 = 1 − 2 1! + 4 2! − 6 3! + · · · and we know that cos = 1 − 2! 2 + 4! 4 − · · · from Equation 16. Therefore, −2 cos = 1 − 2 + 1 24 − · · · 1 − 1 22 + 24 1 4 − · · · . Writing only the terms with degree ≤ 4, we get −2 cos = 1 − 1 22 + 24 1 4 − 2 + 1 24 + 1 24 + · · · = 1 − 3 22 + 25 244 + · · · . 68. sec = 1 cos (16) = 1 1 − 1 22 + 24 1 4 − · · · . 1 + 1 22 + 24 5 4 + · · · 1 − 1 22 + 24 1 4 − · · · 1 1 − 1 22 + 24 1 4 − · · · 1 2 2 − 1 244 + · · · 1 2 2 − 1 44 + · · · 5 244 + · · · 5 244 + · · · · · · From the long division above, sec = 1 + 1 22 + 24 5 4 + · · · . 69. sin (15) = − 1 63 + 120 1 5 − · · ·. 1 + 1 62 + 360 7 4 + · · · − 1 63 + 120 1 5 − · · · − 1 63 + 120 1 5 − · · · 1 6 3 − 1 1205 + · · · 1 6 3 − 1 365 + · · · 7 3605 + · · · 7 3605 + · · · · · · From the long division above, sin = 1 + 1 62 + 360 7 4 + · · · . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.10 TAYLOR AND MACLAURIN SERIES ¤ 1055 70. From Table 1, we have = 1 + 1! + 2 2! + 3 3! + · · · and that ln(1 + ) = − 22 + 33 − 44 + · · · . Therefore, = ln(1 + ) = 1 + 1! + 2! 2 + 3! 3 + · · · − 22 + 33 − 44 + · · · . Writing only terms with degree ≤ 3, we get ln(1 + ) = − 1 2 2 + 1 3 3 + 2 − 1 2 3 + 1 2 3 + · · · = + 1 2 2 + 1 3 3 + · · · . 71. = (arctan)2 = − 1 3 3 + 1 5 5 − 1 7 7 + · · · − 1 3 3 + 1 5 5 − 1 7 7 + · · · . Writing only the terms with degree ≤ 6, we get (arctan)2 = 2 − 1 3 4 + 1 5 6 − 1 3 4 + 1 9 6 + 1 5 6 + · · · = 2 − 2 3 4 + 23 45 6 + · · · . 72. = sin2 = ( sin)sin = + 2 + 1 3 3 + · · · − 1 6 3 + · · · [from Example 13]. Writing only the terms with degree ≤ 4, we get sin2 = 2 − 1 6 4 + 3 + 1 3 4 + · · · = 2 + 3 + 1 6 4 + · · · . 73. ∞ =0 (−1) 4 ! = ∞ =0 −4 ! = −4, by (11). 74. ∞ =0 (−1) 2 62(2)! = ∞ =0 (−1) 6 2 (2)! = cos 6 = √23, by (16). 75. ∞ =1 (−1)−1 3 5 = ∞ =1 (−1)−1 (35) = ln1 + 3 5 [from Table 1] = ln 85 76. ∞ =0 3 5 ! = ∞ =0 (35) ! = 35, by (11). 77. ∞ =0 (−1) 2+1 42+1(2 + 1)! = ∞ =0 (−1) 4 2+1 (2 + 1)! = sin 4 = √12, by (15). 78. 1 − ln 2 + (ln 2)2 2! − (ln 2)3 3! + · · · = ∞ =0 (−ln 2) ! = − ln 2 = ln 2−1 = 2−1 = 1 2, by (11). 79. 3 + 9 2! + 27 3! + 81 4! + · · · = 31 1! + 32 2! + 33 3! + 34 4! + · · · = ∞ =1 3 ! = ∞ =0 3 ! − 1 = 3 − 1, by (11). 80. 1 1 · 2 − 1 3 · 23 + 1 5 · 25 − 1 7 · 27 + · · · = ∞ =0 (−1) 1 (2 + 1)22+1 = ∞ =0 (−1) (12)2+1 2 + 1 = tan−1 1 2 [from Table 1] 81. If is an th-degree polynomial, then ()() = 0 for , so its Taylor series at is () = =0 ()() ! ( − ). Put − = 1, so that = + 1. Then ( + 1) = =0 ()() ! . This is true for any , so replace by : ( + 1) = =0 ()() ! 82. The coefficient of 58 in the Maclaurin series of () = (1 + 3)30 is (58)(0) 58! . But the binomial series for () is (1 + 3)30 = ∞ =0 30 3, so it involves only powers of that are multiples of 3 and therefore the coefficient of 58 is 0. So (58)(0) = 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1056 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 83. Assume that | 000()| ≤ , so 000() ≤ for ≤ ≤ + . Now 000() ≤ ⇒ 00() − 00() ≤ ( − ) ⇒ 00() ≤ 00() + ( − ). Thus, 00() ≤ [ 00() + ( − )] ⇒ 0() − 0() ≤ 00()( − ) + 1 2 ( − )2 ⇒ 0() ≤ 0() + 00()( − ) + 1 2 ( − )2 ⇒ 0() ≤ 0() + 00()( − ) + 1 2 ( − )2 ⇒ () − () ≤ 0()( − ) + 1 2 00()( − )2 + 1 6 ( − )3. So () − () − 0()( − ) − 1 2 00()( − )2 ≤ 1 6 ( − )3. But 2() = () − 2() = () − () − 0()( − ) − 1 2 00()( − )2, so 2() ≤ 1 6 ( − )3. A similar argument using 000() ≥ − shows that 2() ≥ − 1 6 ( − )3. So |2(2)| ≤ 1 6 | − |3. Although we have assumed that , a similar calculation shows that this inequality is also true if . 84. (a) () = 0−12 if if 6= 0 = 0 so 0(0) = lim →0 () − − 0(0) = lim →0 −12 = lim →0 11 2 = lim →0 212 = 0 (using l’Hospital’s Rule and simplifying in the penultimate step). Similarly, we can use the definition of the derivative and l’Hospital’s Rule to show that 00(0) = 0, (3)(0) = 0, , ()(0) = 0, so that the Maclaurin series for consists entirely of zero terms. But since () 6= 0 except for = 0, we see that cannot equal its Maclaurin series except at = 0. (b) From the graph, it seems that the function is extremely flat at the origin. In fact, it could be said to be “infinitely flat” at = 0, since all of its derivatives are 0 there. 85. (a) () = ∞ =0 ⇒ 0() = ∞=1 −1, so (1 + )0() = (1 + ) ∞ =1−1 = ∞=1−1 + ∞=1 = ∞ =0 + 1 ( + 1) + ∞=0 Replace in the first series with + 1 = ∞ =0 ( + 1)( − 1)( − 2)· · · ( − + 1)( − ) ( + 1)! + ∞ =0 ()( − 1)( − 2) !· · ·( − + 1) = ∞ =0 ( + 1)( − 1)( − 2)· · ·( − + 1) ( + 1)! [( − ) + ] = ∞ =0 ( − 1)( − 2)· · · ( − + 1) ! = ∞ =0 = () Thus, 0() = () 1 + . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE LABORATORY PROJECT AN ELUSIVE LIMIT ¤ 1057 (b) () = (1 + )− () ⇒ 0() = −(1 + )−−1() + (1 + )− 0() [Product Rule] = −(1 + )−−1() + (1 + )− () 1 + [from part (a)] = −(1 + )−−1() + (1 + )−−1() = 0 (c) From part (b) we see that () must be constant for ∈ (−11), so () = (0) = 1 for ∈ (−1 1). Thus, () = 1 = (1 + )− () ⇔ () = (1 + ) for ∈ (−1 1). 86. Using the binomial series to expand √1 + as a power series as in Example 9, we get √1 + = (1 + )12 = 1 + 2 + ∞ =2 (−1)−11 · 3 · 5 · · · · · (2 − 3) 2 · ! , so 1 − 212 = 1 − 122 − ∞ =2 1 · 3 · 5 · · · · · (2 − 3) 2 · ! 2 and 1 − 2 sin2 = 1 − 1 2 2 sin2 − ∞ =2 1 · 3 · 5 · · · · · (2 − 3) 2 · ! 2 sin2 . Thus, = 4 021 − 2 sin2 = 4 021 − 122 sin2 − ∞=2 1 · 3 · 5 · · · · · 2 · (2 ! − 3)2 sin2 = 4 2 − 22 1 − ∞=2 1 · 3 · 5 · · · · · ! (2 − 3)22 where = 02 sin2 = 1 · 32 ·· 54 · · · · · · 6 · · · · · (22− 1) 2 by Exercise 7.1.50. = 42 1 − 22 · 12 − ∞=2 1 · 3 · 5 · · · · · ! (2 − 3)22 1 · 32 ·· 54 · · · · · · 6 · · · · · (22− 1) = 21 − 42 − ∞=2 22 · 12 · 32 · 52 · · · · · ! · 2(2 · −! 3)2(2 − 1) = 21 − 42 − ∞=2 42 1 · 3 · · · · · !(2 − 3)2 (2 − 1) = 21 − 42 − 364 4 − 256 56 − · · · = 128 (256 − 642 − 124 − 56 − · · ·) LABORATORY PROJECT An Elusive Limit 1. () = () () = sin(tan) − tan(sin) arcsin(arctan) − arctan(arcsin) The table of function values were obtained using Maple with 10 digits of precision. The results of this project will vary depending on the CAS and precision level. It appears that as → 0+, () → 10 3 . Since is an even function, we have () → 10 3 as → 0. () 1 11838 01 09821 001 20000 0001 33333 00001 33333 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1058 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 2. The graph is inconclusive about the limit of as → 0. 3. The limit has the indeterminate form 0 0. Applying l’Hospital’s Rule, we obtain the form 0 0 six times. Finally, on the seventh application we obtain lim →0 (7)() (7)() = −168 −168 = 1. 4. lim →0 () = lim →0 () () CAS = lim →0 − 1 30 7 − 756 29 9 + · · · − 1 30 7 + 756 13 9 + · · · = lim →0 − 30 1 7 − 756 29 9 + · · · 7 − 30 1 7 + 756 13 9 + · · · 7 = lim →0 − 1 30 − 29 756 2 + · · · − 1 30 + 756 13 2 + · · · = − 1 30 − 1 30 = 1 Note that (7)() = (7)() = − 30 7! = − 5040 30 = −168, which agrees with the result in Problem 3. 5. The limit command gives the result that lim →0 () = 1. 6. The strange results (with only 10 digits of precision) must be due to the fact that the terms being subtracted in the numerator and denominator are very close in value when || is small. Thus, the differences are imprecise (have few correct digits). 11.11 Applications of Taylor Polynomials 1. (a) ()() ()(0) () 0 sin 0 0 1 cos 1 2 −sin 0 3 −cos −1 − 1 6 3 4 sin 0 − 1 6 3 5 cos 1 − 1 6 3 + 120 1 5 Note: () = =0 ()(0) ! (b) 0() 1() = 2() 3() = 4() 5() 4 07071 0 07854 07047 07071 2 1 0 15708 09248 10045 0 0 31416 −20261 05240 (c) As increases, () is a good approximation to () on a larger and larger interval. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.11 APPLICATIONS OF TAYLOR POLYNOMIALS ¤ 1059 2. (a) ()() ()(0) () 0 tan 0 0 1 sec2 1 2 2sec2 tan 0 3 4sec2 tan2 + 2sec4 2 + 1 33 Note: () = =0 ()(0) (b) 0() 1() = 2() 3() ! 6 05774 0 05236 05714 4 1 0 07854 09469 3 17321 0 10472 14300 (c) As increases, () is a good approximation to () on a larger and larger interval. Because the Taylor polynomials are continuous, they cannot approximate the infinite discontinuities at = ±2. They can only approximate tan on (−2 2). 3. ()() ()(1) 0 1 2 3 3() = 3 =0 ()(1) ! ( − 1) = 0! ( − 1)0 + 1! ( − 1)1 + 2! ( − 1)2 + 3! ( − 1)3 = + ( − 1) + 1 2( − 1)2 + 1 6( − 1)3 4. ()() ()(6) 0 sin 12 1 cos √32 2 −sin −12 3 −cos −√32 3() = 3 =0 ()(6) ! − 6 = 12 0! − 6 0 + √1! 32 − 6 1 − 12! 2 − 6 2 + √3! 32 − 6 3 = 1 2 + √3 2 − 6 − 14 − 6 2 − √123 − 6 3 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1060 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 5. ()() ()(2) 0 cos 0 1 −sin −1 2 −cos 0 3 sin 1 3() = 3 =0 ()(2) ! − 2 = − − 2 + 1 6 − 2 3 6. ()() ()(0) 0 − sin 0 1 −(cos − sin) 1 2 −2− cos −2 3 2−(cos + sin) 2 3() = 3 =0 ()(0) ! = − 2 + 1 33 7. ()() ()(1) 0 ln 0 1 1 1 2 −12 −1 3 23 2 3() = 3 =0 ()(1) ! ( − 1) = 0 + 1 1!( − 1) + −2!1( − 1)2 + 3! 2 ( − 1)3 = ( − 1) − 1 2( − 1)2 + 1 3( − 1)3 8. ()() ()(0) 0 cos 0 1 −sin + cos 1 2 −cos − 2sin 0 3 sin − 3cos −3 3() = 3 =0 ()(0) ! = 0 + 1 1! + 0 + −3!33 = − 123 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.11 APPLICATIONS OF TAYLOR POLYNOMIALS ¤ 1061 9. ()() ()(0) 0 −2 0 1 (1 − 2)−2 1 2 4( − 1)−2 −4 3 4(3 − 2)−2 12 3() = 3 =0 ()(0) ! = 0 1 · 1 + 1 11 + −242 + 12 6 3 = − 22 + 23 10. ()() ()(1) 0 tan−1 4 1 1 1 + 2 1 2 2 −2 (1 + 2)2 − 1 2 3 62 − 2 (1 + 2)3 1 2 3() = 3 =0 ()(1) ! ( − 1) = 4 + 112( − 1)1 + −122( − 1)2 + 1 62( − 1)3 = 4 + 1 2( − 1) − 1 4( − 1)2 + 12 1 ( − 1)3 11. You may be able to simply find the Taylor polynomials for () = cot using your CAS. We will list the values of ()(4) for = 0 to = 5. 0 1 2 3 4 5 ()(4) 1 −2 4 −16 80 −512 5() = 5 =0 ()(4) ! − 4 = 1 − 2 − 4 + 2 − 4 2 − 8 3 − 4 3 + 10 3 − 4 4 − 64 15 − 4 5 For = 2 to = 5, () is the polynomial consisting of all the terms up to and including the − 4 term 12. You may be able to simply find the Taylor polynomials for () = √3 1 + 2 using your CAS. We will list the values of ()(0) for = 0 to = 5. 0 1 2 3 4 5 ()(0) 1 0 2 3 0 − 8 3 0 5() = 5 =0 ()(0) ! = 1 + 1 32 − 1 94 For = 2 to = 5, () is the polynomial consisting of all the terms up to and including the term. Note that 2 = 3 and 4 = 5. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1062 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 13. (a) ()() ()(1) 0 1 1 1 −12 −1 2 23 2 3 −64 () = 1 ≈ 2() = 1 0! ( − 1)0 − 1! 1 ( − 1)1 + 2! 2 ( − 1)2 = 1 − ( − 1) + ( − 1)2 (b) |2()| ≤ 3! | − 1|3, where | 000()| ≤ . Now 07 ≤ ≤ 13 ⇒ | − 1| ≤ 03 ⇒ | − 1|3 ≤ 0027. Since | 000()| is decreasing on [0713], we can take = | 000(07)| = 6(07)4, so |2()| ≤ 6(07)4 6 (0027) = 0112 453 1. (c) From the graph of |2()| = 1 − 2() , it seems that the error is less than 0038 571 on [07 13]. 14. (a) ()() ()(4) 0 −12 1 2 1 − 1 2−32 − 16 1 2 3 4−52 128 3 3 − 15 8 −72 () = −12 ≈ 2() = 12 0! ( − 4)0 − 11! 16( − 4)1 + 32! 128( − 4)2 = 1 2 − 1 16( − 4) + 256 3 ( − 4)2 (b) |2()| ≤ 3! | − 4|3, where | 000()| ≤ . Now 35 ≤ ≤ 45 ⇒ | − 4| ≤ 05 ⇒ | − 4|3 ≤ 0125. Since | 000()| is decreasing on [3545], we can take = | 000(35)| = 15 8(35)72 , so |2()| ≤ 15 6 · 8(35)72 (0125) ≈ 0000 487. (c) From the graph of |2()| = −12 − 2() , it seems that the error is less than 0000 343 on [3545]. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.11 APPLICATIONS OF TAYLOR POLYNOMIALS ¤ 1063 15. ()() ()(1) 0 23 1 1 2 3−13 2 3 2 − 2 9−43 − 2 9 3 8 27−73 27 8 4 − 56 81−103 (a) () = 23 ≈ 3() = 1 + 2 3( − 1) − 22! 9( − 1)2 + 83! 27( − 1)3 = 1 + 2 3( − 1) − 1 9( − 1)2 + 81 4 ( − 1)3 (b) |3()| ≤ 4! | − 1|4, where (4)() ≤ . Now 08 ≤ ≤ 12 ⇒ | − 1| ≤ 02 ⇒ | − 1|4 ≤ 00016. Since (4)() is decreasing on [08 12], we can take = (4)(08) = 56 81(08)−103, so |3()| ≤ 56 81(08)−103 24 (00016) ≈ 0000 096 97. (c) From the graph of |3()| = 23 − 3() , it seems that the error is less than 0000 053 3 on [0812]. 16. ()() ()(6) 0 sin 12 1 cos √32 2 −sin −12 3 −cos −√32 4 sin 12 5 cos (a) () = sin ≈ 4() = 1 2 + √3 2 − 6 − 1 4 − 6 2 − √123 − 6 3 + 48 1 − 6 4 (b) |4()| ≤ 5! − 6 5 , where (5)() ≤ . Now 0 ≤ ≤ 3 ⇒ − 6 ≤ − 6 ≤ 6 ⇒ − 6 ≤ 6 ⇒ − 6 5 ≤ 6 5. Since (5)() is decreasing on 0 3 , we can take = (5)(0) = cos 0 = 1, so |4()| ≤ 1 5!6 5 ≈ 0000 328. (c) From the graph of |4()| = |sin − 4()|, it seems that the error is less than 0000 297 on 0 3 . 17. ()() ()(0) 0 sec 1 1 sec tan 0 2 sec(2 sec2 − 1) 1 3 sec tan(6 sec2 − 1) (a) () = sec ≈ 2() = 1 + 1 22 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1064 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES (b) |2()| ≤ 3! ||3, where (3)() ≤ . Now −02 ≤ ≤ 02 ⇒ || ≤ 02 ⇒ ||3 ≤ (02)3. (3)() is an odd function and it is increasing on [002] since sec and tan are increasing on [002], so (3)() ≤ (3)(02) ≈ 1085 158 892. Thus, |2()| ≤ (3)3! (02) (02)3 ≈ 0001 447. (c) From the graph of |2()| = |sec − 2()|, it seems that the error is less than 0000 339 on [−0202]. 18. ()() ()(1) 0 ln(1 + 2) ln 3 1 2(1 + 2) 2 3 2 −4(1 + 2)2 − 4 9 3 16(1 + 2)3 16 27 4 −96(1 + 2)4 (a) () = ln(1 + 2) ≈ 3() = ln 3 + 2 3( − 1) − 42! 9( − 1)2 + 163! 27( − 1)3 (b) |3()| ≤ 4! | − 1|4, where (4)() ≤ . Now 05 ≤ ≤ 15 ⇒ −05 ≤ − 1 ≤ 05 ⇒ | − 1| ≤ 05 ⇒ | − 1|4 ≤ 16 1 , and letting = 05 gives = 6, so |3()| ≤ 6 4! · 1 16 = 1 64 = 0015 625. (c) From the graph of |3()| = |ln(1 + 2) − 3()|, it seems that the error is less than 0005 on [05 15]. 19. ()() ()(0) 0 2 1 1 2(2) 0 2 2(2 + 42) 2 3 2(12 + 83) 0 4 2(12 + 482 + 164) (a) () = 2 ≈ 3() = 1 + 2 2!2 = 1 + 2 (b) |3()| ≤ 4! ||4, where (4)() ≤ . Now 0 ≤ ≤ 01 ⇒ 4 ≤ (01)4, and letting = 01 gives |3()| ≤ 001 (12 + 048 + 00016) 24 (01)4 ≈ 000006. (c) From the graph of |3()| = 2 − 3() , it appears that the error is less than 0000 051 on [001]. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.11 APPLICATIONS OF TAYLOR POLYNOMIALS ¤ 1065 20. ()() ()(1) 0 ln 0 1 ln + 1 1 2 1 1 3 −12 −1 4 23 (a) () = ln ≈ 3() = ( − 1) + 1 2( − 1)2 − 1 6( − 1)3 (b) |3()| ≤ 4! | − 1|4, where (4)() ≤ . Now 05 ≤ ≤ 15 ⇒ | − 1| ≤ 1 2 ⇒ | − 1|4 ≤ 16 1 . Since (4)() is decreasing on [0515], we can take = (4)(05) = 2(05)3 = 16, so |3()| ≤ 16 24(116) = 24 1 = 00416. (c) From the graph of |3()| = |ln − 3()|, it seems that the error is less than 00076 on [0515]. 21. ()() ()(0) 0 sin 0 1 sin + cos 0 2 2cos − sin 2 3 −3sin − cos 0 4 −4cos + sin −4 5 5sin + cos (a) () = sin ≈ 4() = 2 2!( − 0)2 + −4!4( − 0)4 = 2 − 164 (b) |4()| ≤ 5! ||5, where (5)() ≤ . Now −1 ≤ ≤ 1 ⇒ || ≤ 1, and a graph of (5)() shows that (5)() ≤ 5 for −1 ≤ ≤ 1. Thus, we can take = 5 and get |4()| ≤ 5 5! · 15 = 24 1 = 00416. (c) From the graph of |4()| = |sin − 4()|, it seems that the error is less than 00082 on [−11]. 22. ()() ()(0) 0 sinh 2 0 1 2cosh2 2 2 4sinh2 0 3 8cosh2 8 4 16 sinh 2 0 5 32 cosh 2 32 6 64 sinh 2 (a) () = sinh 2 ≈ 5() = 2 + 3! 8 3 + 32 5! 5 = 2 + 4 33 + 15 4 5 (b) |5()| ≤ 6! ||6, where (6)() ≤ . For in [−11], we have || ≤ 1. Since (6)() is an increasing odd function on [−1 1], we see that (6)() ≤ (6)(1) = 64 sinh 2 = 32(2 − −2) ≈ 232119, so we can take = 23212 and get |5()| ≤ 232 720 12 · 16 ≈ 03224. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1066 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES (c) From the graph of |5()| = |sinh2 − 5()|, it seems that the error is less than 0027 on [−1 1]. 23. From Exercise 5, cos = − − 2 + 1 6 − 2 3 + 3(), where |3()| ≤ 4! − 2 4 with (4)() = |cos | ≤ = 1. Now = 80◦ = (90◦ − 10◦) = 2 − 18 = 49 radians, so the error is 3 49 ≤ 24 1 18 4 ≈ 0000 039, which means our estimate would not be accurate to five decimal places. However, 3 = 4, so we can use 4 49 ≤ 120 1 18 5 ≈ 0000001. Therefore, to five decimal places, cos80◦ ≈ − − 18 + 1 6 − 18 3 ≈ 017365. 24. From Exercise 16, sin = 1 2 + √23 − 6 − 1 4 − 6 2 − √123 − 6 3 + 48 1 − 6 4 + 4(), where |4()| ≤ 5! − 6 5 with (5)() = |cos| ≤ = 1. Now = 38◦ = (30◦ + 8◦) = 6 + 245 radians, so the error is 4 38 180 ≤ 120 1 245 5 ≈ 000000044, which means our estimate will be accurate to five decimal places. Therefore, to five decimal places, sin38◦ = 1 2 + √23 245 − 1 4 245 2 − √123 245 3 + 48 1 245 4 ≈ 061566. 25. All derivatives of are , so |()| ≤ ( + 1)! ||+1, where 0 01. Letting = 01, (01) ≤ 01 ( + 1)!(01)+1 000001, and by trial and error we find that = 3 satisfies this inequality since 3(01) 00000046. Thus, by adding the four terms of the Maclaurin series for corresponding to = 0, 1, 2, and 3, we can estimate 01 to within 000001. (In fact, this sum is 110516 and 01 ≈ 110517.) 26. From Table 1 in Section 11.10, ln(1 + ) = ∞ =1 (−1)−1 for || 1. Thus, ln14 = ln(1 + 04) = ∞ =1 (−1)−1 (04) . Since this is an alternating series, the error is less than the first neglected term by the Alternating Series Estimation Theorem, and we find that |6| = (04)66 ≈ 00007 0001. So we need the first five (nonzero) terms of the Maclaurin series for the desired accuracy. (In fact, this sum is approximately 033698 and ln14 ≈ 033647.) 27. sin = − 1 3!3 + 5! 1 5 − · · · . By the Alternating Series Estimation Theorem, the error in the approximation sin = − 1 3!3 is less than 1 5!5 001 ⇔ 5 120(001) ⇔ || (12)15 ≈ 1037. The curves = − 1 63 and = sin − 001 intersect at ≈ 1043, so the graph confirms our estimate. Since both the sine function °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.11 APPLICATIONS OF TAYLOR POLYNOMIALS ¤ 1067 and the given approximation are odd functions, we need to check the estimate only for 0. Thus, the desired range of values for is −1037 1037. 28. cos = 1 − 1 2!2 + 4! 1 4 − 6! 1 6 + · · · . By the Alternating Series Estimation Theorem, the error is less than − 1 6!6 0005 ⇔ 6 720(0005) ⇔ || (36)16 ≈ 1238. The curves = 1 − 1 22 + 24 1 4 and = cos + 0005 intersect at ≈ 1244, so the graph confirms our estimate. Since both the cosine function and the given approximation are even functions, we need to check the estimate only for 0. Thus, the desired range of values for is −1238 1238. 29. arctan = − 3 3 + 5 5 − 7 7 + · · · . By the Alternating Series Estimation Theorem, the error is less than − 1 77 005 ⇔ 7 035 ⇔ || (035)17 ≈ 08607. The curves = − 1 33 + 1 55 and = arctan + 005 intersect at ≈ 09245, so the graph confirms our estimate. Since both the arctangent function and the given approximation are odd functions, we need to check the estimate only for 0. Thus, the desired range of values for is −086 086. 30. () = ∞ =0 ()(4) ! ( − 4) = ∞ =0 (−1) ! 3( + 1)!( − 4) = ∞ =0 (−1) 3( + 1)( − 4). Now (5) = ∞ =0 (−1) 3( + 1) = ∞ =0 (−1) is the sum of an alternating series that satisfies (i) +1 ≤ and (ii) lim →∞ = 0, so by the Alternating Series Estimation Theorem, |5(5)| = |(5) − 5(5)| ≤ 6, and 6 = 1 36(7) = 1 5103 ≈ 0000196 00002; that is, the fifth-degree Taylor polynomial approximates (5) with error less than 00002. 31. Let () be the position function of the car, and for convenience set (0) = 0. The velocity of the car is () = 0() and the acceleration is () = 00(), so the second degree Taylor polynomial is 2() = (0) + (0) + (0) 2 2 = 20 + 2. We estimate the distance traveled during the next second to be (1) ≈ 2(1) = 20 + 1 = 21 m. The function 2() would not be accurate over a full minute, since the car could not possibly maintain an acceleration of 2 ms2 for that long (if it did, its final speed would be 140 ms ≈ 313 mih!). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1068 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 32. (a) ()() ()(20) 0 20(−20) 20 1 20(−20) 20 2 220(−20) 220 The linear approximation is 1() = (20) + 0(20)( − 20) = 20[1 + ( − 20)] The quadratic approximation is 2() = (20) + 0(20)( − 20) + 00(20) 2 ( − 20)2 = 201 + ( − 20) + 1 22( − 20)2 (b) (c) From the graph, it seems that 1() is within 1% of (), that is, 099() ≤ 1() ≤ 101(), for −14◦C ≤ ≤ 58◦C. 33. = 2 − ( + )2 = 2 − 2(1 + )2 = 2 1 − 1 + −2. We use the Binomial Series to expand (1 + )−2: = 2 1 − 1 − 2 + 22! · 3 2 − 2 ·3! 3 · 4 3 + · · · = 2 2 − 3 2 + 4 3 − · · · ≈ 2 · 2 = 2 · 13 when is much larger than ; that is, when is far away from the dipole. 34. (a) 1 + 2 = 1 2 − 1 [Equation 1] where = 2 + ( + )2 − 2( + )cos and = 2 + ( − )2 + 2( − )cos (2) Using cos ≈ 1 gives = 2 + ( + )2 − 2( + ) = 2 + 2 + 2 + 2 − 2 − 22 = 2 = and similarly, = . Thus, Equation 1 becomes 1 + 2 = 1 2 − 1 ⇒ 1 + 2 = 2 − 1 . (b) Using cos ≈ 1 − 1 22 in (2) gives us = 2 + ( + )2 − 2( + )1 − 1 22 = 2 + 2 + 2 + 2 − 2 + 2 − 22 + 22 = 2 + 2 + 22 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.11 APPLICATIONS OF TAYLOR POLYNOMIALS ¤ 1069 Anticipating that we will use the binomial series expansion (1 + ) ≈ 1 + , we can write the last expression for as 1 + 2 + 2 2 and similarly, = 1 − 2 − 2 2 . Thus, from Equation 1, 1 + 2 = 1 2 − 1 ⇔ 1− 1 + 2− 1 = 2 · − 1 · ⇔ 1 1 + 2 + 2 2 −12 + 2 1 − 2 − 2 2 −12 = 2 1 − 2 − 2 2 −12 − 1 1 + 2 + 2 2 −12 Approximating the expressions for − 1 and − 1 by the first two terms in their binomial series, we get 1 1 − 1 22 + 2 2 + 2 1 + 1 22 − 2 2 = 2 1 + 1 22 − 2 2 − 1 1 − 1 22 + 2 2 ⇔ 1 − 12 2 + 2 2 + 2 + 222 − 2 2 = 2 + 222 − 2 2 − 1 + 212 + 2 2 ⇔ 1 + 2 = 2 − 1 + 12 2 + 2 2 + 212 + 2 2 + 222 − 2 2 − 222 − 2 2 = 2 − 1 + 12 2 + 2 2 1 + 1 + 222 − 2 2 1 − 1 = 2 − 1 + 122 2 1 + 1 1 + 1 + 2222 1 − 1 1 − 1 = 2 − 1 + 22 21 1 + 1 2 + 22 1 − 1 2 From Figure 8, we see that sin = . So if we approximate sin with , we get = and 2 = 22 and hence, Equation 4, as desired. 35. (a) If the water is deep, then 2 is large, and we know that tanh → 1 as → ∞. So we can approximate tanh(2) ≈ 1, and so 2 ≈ (2) ⇔ ≈ (2). (b) From the table, the first term in the Maclaurin series of tanh is , so if the water is shallow, we can approximate tanh 2 ≈ 2 , and so 2 ≈ 2 · 2 ⇔ ≈ √. ()() ()(0) 0 tanh 0 1 sech2 1 2 −2sech2 tanh 0 3 2sech2 (3 tanh2 − 1) −2 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1070 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES (c) Since tanh is an odd function, its Maclaurin series is alternating, so the error in the approximation tanh 2 ≈ 2 is less than the first neglected term, which is | 000 3! (0)|23 = 1323. If 10, then 1 323 132 · 10 1 3 = 375 3 , so the error in the approximation 2 = is less than 2 · 3 375 ≈ 00132. 36. First note that 2√2 + 2 − = 2√21 + 22 − ≈ 21 + 22 · 12 + · · · − use the binomial series 1 + 1 2 + · · · for √1 + = 2 + 22 + · · · − ≈ 2 since for large the other terms are comparatively small. Now = 2√2 + 2 − ≈ 2 by the preceding approximation. 37. (a) is the length of the arc subtended by the angle , so = ⇒ = . Now sec = ( + ) ⇒ sec = + ⇒ = sec − = sec() − . (b) First we’ll find a Taylor polynomial 4() for () = sec at = 0. ()() ()(0) 0 sec 1 1 sectan 0 2 sec(2 tan2 + 1) 1 3 sectan(6 tan2 + 5) 0 4 sec(24 tan4 + 28 tan2 + 5) 5 Thus, () = sec ≈ 4() = 1 + 2! 1 ( − 0)2 + 4! 5 ( − 0)4 = 1 + 1 22 + 24 5 4. By part (a), ≈ 1 + 12 2 + 24 5 4 − = + 1 2 · 22 + 24 5 · 44 − = 22 + 24 543 . (c) Taking = 100 km and = 6370 km, the formula in part (a) says that = sec() − = 6370 sec(1006370) − 6370 ≈ 0785 009 965 44 km. The formula in part (b) says that ≈ 2 2 + 54 243 = 1002 2 · 6370 + 5 · 1004 24 · 63703 ≈ 0785 009 957 36 km. The difference between these two results is only 0000 000 008 08 km, or 0000 008 08 m! °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE SECTION 11.11 APPLICATIONS OF TAYLOR POLYNOMIALS ¤ 1071 38. (a) 4 02 1 − 2 sin2 = 4 02 1 + −2 sin2 −12 = 4 02 1 − 12−2 sin2 + 1 22! · 3 2 −2 sin2 2 − 1 2 ·3! 3 2 · 5 2 −2 sin2 3 + · · · = 4 02 1 + 122 sin2 + 12 ·· 344 sin4 + 1 2 · · 3 4 · · 5 66 sin6 + · · · = 4 2 + 211 2 · 2 2 + 12 ·· 3412 ·· 34 · 2 4 + 1 2 · · 3 4 · · 5 612 ·· 34 ·· 56 · 2 6 + · · · [split up the integral and use the result from Exercise 7.1.50] = 2 1 + 122 2 2 + 122 2 · · 3 42 2 4 + 122 2 · · 3 42 2 · · 5 62 2 6 + · · · (b) The first of the two inequalities is true because all of the terms in the series are positive. For the second, = 2 1 + 122 2 2 + 1 22 2 · · 3 42 2 4 + 1 22 2 · · 3 42 2 · · 5 62 2 6 + 1 22 2 · · 3 42 2 · · 5 62 2 · · 7 82 2 8 + · · · ≤ 2 1 + 1 42 + 1 44 + 1 46 + 1 48 + · · · The terms in brackets (after the first) form a geometric series with = 1 42 and = 2 = sin2 1 20 1. So ≤ 2 1 + 1−242 = 2 4 4 − − 3 4 2 2 . (c) We substitute = 1, = 98, and = sin(10◦2) ≈ 008716, and the inequality from part (b) becomes 201090 ≤ ≤ 201093, so ≈ 20109. The estimate ≈ 2 ≈ 20071 differs by about 02%. If 0 = 42◦, then ≈ 035837 and the inequality becomes 207153 ≤ ≤ 208103, so ≈ 20763. The one-term estimate is the same, and the discrepancy between the two estimates increases to about 34%. 39. Using () = () + () with = 1 and = , we have () = 1() + 1(), where 1 is the first-degree Taylor polynomial of at . Because = , () = () + 0()( − ) + 1(). But is a root of , so () = 0 and we have 0 = () + 0()( − ) + 1(). Taking the first two terms to the left side gives us 0()( − ) − () = 1(). Dividing by 0(), we get − − () 0() = 1() 0(). By the formula for Newton’s method, the left side of the preceding equation is +1 − , so |+1 − | = 1() 0() . Taylor’s Inequality gives us |1()| ≤ | 00()| 2! | − |2. Combining this inequality with the facts | 00()| ≤ and | 0()| ≥ gives us |+1 − | ≤ 2 | − |2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1072 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES APPLIED PROJECT Radiation from the Stars 1. If we write () = 8−5 ( ) − 1 = −5 ( ) − 1, then as → 0+, it is of the form ∞∞, and as → ∞ it is of the form 00, so in either case we can use l’Hospital’s Rule. First of all, lim →∞ () = lim H →∞ −5−6 − ()2 ( ) = 5 lim →∞ 2( −6) = 5 lim →∞ − ( 4 ) = 0 Also, lim →0+ () = 5 H lim →0+ (− 4 ) = 5 H lim →0+ −4−5 − ()2 ( ) = 20 2 2 lim →0+ −3 ( ) This is still indeterminate, but note that each time we use l’Hospital’s Rule, we gain a factor of in the numerator, as well as a constant factor, and the denominator is unchanged. So if we use l’Hospital’s Rule three more times, the exponent of in the numerator will become 0. That is, for some {}, all constant, lim →0+ () =H 1 lim →0+ −3 ( ) H= 2 lim →0+ −2 ( ) H= 3 lim →0+ −1 ( ) H= 4 lim →0+ 1 ( ) = 0 2. We expand the denominator of Planck’s Law using the Taylor series = 1 + + 2 2! + 3 3! + · · · with = , and use the fact that if is large, then all subsequent terms in the Taylor expansion are very small compared to the first one, so we can approximate using the Taylor polynomial 1: () = 8−5 ( ) − 1 = 8−5 1 + + 2! 1 2 + 3! 1 3 + · · · − 1 ≈ 8−5 1 + − 1 = 8 4 which is the Rayleigh-Jeans Law. 3. To convert to m, we substitute 106 for in both laws. The first figure shows that the two laws are similar for large . The second figure shows that the two laws are very different for short wavelengths (Planck’s Law gives a maximum at ≈ 051 m; the Rayleigh-Jeans Law gives no minimum or maximum.). 4. From the graph in Problem 3, () has a maximum under Planck’s Law at ≈ 051m. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE CHAPTER 11 REVIEW ¤ 1073 5. As gets larger, the total area under the curve increases, as we would expect: the hotter the star, the more energy it emits. Also, as increases, the -value of the maximum decreases, so the higher the temperature, the shorter the peak wavelength (and consequently the average wavelength) of light emitted. This is why Sirius is a blue star and Betelgeuse is a red star: most of Sirius’s light is of a fairly short wavelength; that is, a higher frequency, toward the blue end of the spectrum, whereas most of Betelgeuse’s light is of a lower frequency, toward the red end of the spectrum. 11 Review 1. False. See Note 2 after Theorem 11.2.6. 2. False. The series ∞ =1 − sin 1 = ∞ =1 1 sin 1 is a -series with = sin1 ≈ 084 ≤ 1, so the series diverges. 3. True. If lim →∞ = , then as → ∞, 2 + 1 → ∞, so 2+1 → . 4. True by Theorem 11.8.4. Or: Use the Comparison Test to show that (−2) converges absolutely. 5. False. For example, take = (−1)(6). 6. True by Theorem 11.8.4. 7. False, since lim →∞ +1 = lim →∞ 1 ( + 1)3 · 3 1 = lim →∞ 3 ( + 1)3 · 13 13 = lim →∞ 1 (1 + 1)3 = 1. 8. True, since lim →∞ +1 = lim →∞ 1 ( + 1)! · ! 1 = lim →∞ 1 + 1 = 0 1. 9. False. See the note after Example 11.4.2. 10. True, since 1 = −1and = ∞ =0 ! , so −1 = ∞ =0 (−1) ! . 11. True. See (9) in Section 11.1. 12. True, because if || is convergent, then so is by Theorem 11.6.3. 13. True. By Theorem 11.10.5 the coefficient of 3 is 000(0) 3! = 1 3 ⇒ 000(0) = 2. Or: Use Theorem 11.9.2 to differentiate three times. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1074 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 14. False. Let = and = −. Then {} and {} are divergent, but + = 0, so { + } is convergent. 15. False. For example, let = = (−1). Then {} and {} are divergent, but = 1, so {} is convergent. 16. True by the Monotonic Sequence Theorem, since {} is decreasing and 0 ≤ 1 for all ⇒ {} is bounded. 17. True by Theorem 11.6.3. [(−1) is absolutely convergent and hence convergent.] 18. True. lim →∞ +1 1 ⇒ converges (Ratio Test) ⇒ lim →∞ = 0 [Theorem 11.2.6]. 19. True. 099999 = 09 + 09(01)1 + 09(01)2 + 09(01)3 + · · · = ∞ =1 (09)(01)−1 = 09 1 − 01 = 1 by the formula for the sum of a geometric series [ = 1(1 − )] with ratio satisfying || 1. 20. True. Since lim →∞ = 2, we know that lim →∞ +3 = 2. Thus, lim →∞ (+3 − ) = lim →∞ +3 − lim →∞ = 2 − 2 = 0. 21. True. A finite number of terms doesn’t affect convergence or divergence of a series. 22. False. Let = (01) and = (02). Then ∞ =1 = ∞ =1 (01) = 01 1 − 01 = 1 9 = , ∞ =1 = ∞ =1 (02) = 02 1 − 02 = 1 4 = , and ∞ =1 = ∞ =1 (002) = 002 1 − 002 = 1 49, but = 1 9 · 1 4 = 1 36. 1. 1 + 2 2 + 33 converges since lim →∞ 1 + 2 2 + 33 = lim →∞ 2 1 3 3 + 1 + 2 = 12. 2. = 9+1 10 = 9 · 10 9 , so lim →∞ = 9 lim →∞ 10 9 = 9 · 0 = 0 by (11.1.9). 3. lim →∞ = lim →∞ 3 1 + 2 = lim →∞ 12 + 1 = ∞, so the sequence diverges. 4. = cos(2), so = 0 if is odd and = ±1 if is even. As increases, keeps cycling through the values 0, 1, 0, −1, so the sequence {} is divergent. 5. || = sin 2 + 1 ≤ 2 + 1 1 , so || → 0 as → ∞. Thus, lim →∞ = 0. The sequence {} is convergent. 6. = ln √. Let () = ln √ for 0. Then lim →∞ () = lim →∞ ln √ = lim H →∞ 1(2 1 √) = lim →∞ √2 = 0. Thus, by Theorem 11.1.3, {} converges and lim →∞ = 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE CHAPTER 11 REVIEW ¤ 1075 7. 1 + 3 4 is convergent. Let = 1 + 34. Then lim →∞ ln = lim →∞ 4ln(1 + 3) = lim →∞ ln(1 + 3) 1(4) H = lim →∞ 1 1 + 3 −32 −1(42) = lim →∞ 1 + 3 12 = 12, so lim →∞ = lim →∞1 + 3 4 = 12. 8. (−10) ! converges, since 10 ! = 101··10 2 ··310 · · · · · · · · · · 1010 · 10 11··10 12· · · · · · · · · ·10 ≤ 101010 11−10 → 0 as → ∞, so lim →∞ (−10) ! = 0 [Squeeze Theorem]. Or: Use (11.10.10). 9. We use induction, hypothesizing that −1 2. Note first that 1 2 = 1 3 (1 + 4) = 5 3 2, so the hypothesis holds for = 2. Now assume that −1 2. Then = 1 3(−1 + 4) 1 3( + 4) 1 3(2 + 4) = 2. So +1 2, and the induction is complete. To find the limit of the sequence, we note that = lim →∞ = lim →∞ +1 ⇒ = 1 3( + 4) ⇒ = 2. 10. lim →∞ 4 H = lim →∞ 43 H = lim →∞ 122 H = lim →∞ 24 H = lim →∞ 24 = 0 Then we conclude from Theorem 11.1.3 that lim →∞ 4− = 0. From the graph, it seems that 124−12 01, but 4− 01 whenever 12. So the smallest value of corresponding to = 01 in the definition of the limit is = 12. 11. 3 + 1 3 = 1 2 , so ∞ =1 3 + 1 converges by the Comparison Test with the convergent -series ∞ =1 1 2 [ = 2 1]. 12. Let = 2 + 1 3 + 1 and = 1 , so lim →∞ = lim →∞ 33 ++ 1 = lim →∞ 1 + 1 1 + 1 2 3 = 1 0. Since ∞ =1 is the divergent harmonic series, ∞ =1 also diverges by the Limit Comparison Test. 13. lim →∞ +1 = lim →∞(5+ 1) +1 3 · 53 = lim →∞1 + 1 3 · 15 = 1 5 1, so ∞=1 53 converges by the Ratio Test. 14. Let = √1+ 1. Then is positive for ≥ 1, the sequence {} is decreasing, and lim →∞ = 0, so the series ∞ =1 (−1) √ + 1 converges by the Alternating Series Test. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1076 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 15. Let () = 1 √ln. Then is continuous, positive, and decreasing on [2 ∞), so the Integral Test applies. 2∞ () = lim →∞2 √1ln = ln , = 1 = lim →∞ln 2 ln −12 = lim →∞2√ ln ln 2 = lim →∞2√ln − 2√ln 2 = ∞ so the series ∞ =2 1 √ln diverges. 16. lim →∞ 3 + 1 = 1 3 , so lim →∞ ln3+ 1 = ln 1 3 6= 0. Thus, the series ∞=1ln3+ 1 diverges by the Test for Divergence. 17. || = cos 3 1 + (12) ≤ 1 1 + (12) 1 (12) = 56, so ∞=1|| converges by comparison with the convergent geometric series ∞ =1 5 6 = 5 6 1. It follows that ∞ =1 converges (by Theorem 11.6.3). 18. lim →∞ || = lim →∞ (1 + 2 22) = lim →∞ 1 + 2 22 = lim →∞ 121+ 2 = 12 1, so ∞=1 (1 + 2 22) converges by the Root Test. 19. lim →∞ +1 = lim →∞ 1 · 3 · 5 · ··· · (2 − 1)(2 + 1) 5+1 ( + 1)! · 5 ! 1 · 3 · 5 · · · · · (2 − 1) = lim →∞ 5( 2 + 1 + 1) = 2 5 1, so the series converges by the Ratio Test. 20. ∞ =1 (−5)2 2 9 = ∞ =1 1 2 25 9 . Now lim →∞ +1 = lim →∞ ( + 1) 252+1 · 9+1 · 225·9 = lim →∞ 9(25+ 1) 2 2 = 25 9 1, so the series diverges by the Ratio Test. 21. = √ + 1 0, {} is decreasing, and lim →∞ = 0, so the series ∞ =1 (−1)−1 √ + 1 converges by the Alternating Series Test. 22. Use the Limit Comparison Test with = √ + 1 − √ − 1 = 2 √ + 1 + √ − 1 (rationalizing the numerator) and = 1 32 . lim →∞ = lim →∞ √ + 1 + 2√√ − 1 = 1, so since∞=1 converges = 3 2 1, ∞=1 converges also. 23. Consider the series of absolute values: ∞ =1 −13 is a p-series with = 1 3 ≤ 1 and is therefore divergent. But if we apply the Alternating Series Test, we see that = √31 0, {} is decreasing, and lim →∞ = 0, so the series ∞=1(−1)−1 −13 converges. Thus, ∞ =1 (−1)−1 −13 is conditionally convergent. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE CHAPTER 11 REVIEW ¤ 1077 24. ∞ =1 (−1)−1 −3 = ∞ =1 −3 is a convergent p-series [ = 3 1]. Therefore, ∞ =1 (−1)−1 −3 is absolutely convergent. 25. +1 = (−1)+1( + 2)3+1 22+3 · 22+1 (−1)( + 1)3 = + 2 + 1 · 3 4 = 1 + (2) 1 + (1) · 3 4 → 3 4 1 as → ∞, so by the Ratio Test, ∞ =1 (−1)( + 1)3 22+1 is absolutely convergent. 26. lim →∞ √ ln H = lim →∞ 1(2√) 1 = lim →∞ √ 2 = ∞. Therefore, lim →∞ (−1) √ ln 6= 0, so the given series is divergent by the Test for Divergence. 27. ∞ =1 (−3)−1 23 = ∞ =1 (−3)−1 (23) = ∞ =1 (−3)−1 8 = 1 8 ∞ =1 (−3)−1 8−1 = 1 8 ∞ =1 −38−1 = 181 − (−1 38) = 1 8 · 8 11 = 1 11 28. ∞ =1 1 ( + 3) = ∞ =1 31 − 3(1+ 3) [partial fractions]. = =1 31 − 3( 1+ 3) = 1 3 + 1 6 + 19 − 3(1+ 1) − 3(1+ 2) − 3(1+ 3) (telescoping sum), so ∞ =1 1 ( + 3) = lim →∞ = 13 + 1 6 + 1 9 = 11 18. 29. ∞ =1 [tan−1( + 1) − tan−1 ] = lim →∞ = lim →∞ [(tan−1 2 − tan−1 1) + (tan−1 3 − tan−1 2) + · · · + (tan−1( + 1) − tan−1 )] = lim →∞ [tan−1( + 1) − tan−1 1] = 2 − 4 = 4 30. ∞ =0 (−1) 32 (2)! = ∞ =0 (−1) 1 (2)! · 32 = ∞ =0 (−1) 1 (2)! · √32 = cos√3 since cos = ∞=0(−1) (2 2 )! for all . 31. 1 − + 2 2! − 3 3! + 4 4! − · · · = ∞ =0 (−1) ! = ∞ =0 (−) ! = − since = ∞ =0 ! for all . 32. 417326 = 417 + 326 105 + 326 108 + · · · = 417 + 1326 − 110 1053 = 417 100 + 99326 ,900 = 416 99,900 ,909 33. cosh = 1 2 ( + −) = 1 2∞=0 ! + ∞=0 (−!) = 1 2 1 + + 2! 2 + 3! 3 + 4! 4 + · · · + 1 − + 2! 2 − 3! 3 + 4! 4 − · · · = 1 2 2 + 2 · 2! 2 + 2 · 4! 4 + · · · = 1 + 1 22 + ∞=2 (2 2)! ≥ 1 + 1 22 for all °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1078 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 34. ∞ =1 (ln) is a geometric series which converges whenever |ln| 1 ⇒ −1 ln 1 ⇒ −1 . 35. ∞ =1 (−1)+1 5 = 1 − 32 1 + 243 1 − 1024 1 + 3125 1 − 7776 1 + 16,1807 − 32,1768 + · · · . Since 8 = 1 85 = 1 32,768 0000031, ∞ =1 (−1)+1 5 ≈ 7 =1 (−1)+1 5 ≈ 09721. 36. (a) 5 = 5 =1 1 6 = 1 + 1 26 + · · · + 1 65 ≈ 1017305. The series ∞ =1 1 6 converges by the Integral Test, so we estimate the remainder 5 with (11.3.2): 5 ≤ 5∞ 6 = −− 5 5 ∞ 5 = 5−55 = 0000064. So the error is at most 0000064. (b) In general, ≤ ∞ 6 = 515 . If we take = 9, then 9 ≈ 101734 and 9 ≤ 5 ·195 ≈ 34 × 10−6. So to five decimal places, ∞ =1 1 5 ≈ 9 =1 1 5 ≈ 101734. Another method: Use (11.3.3) instead of (11.3.2). 37. ∞ =1 1 2 + 5 ≈ 8 =1 1 2 + 5 ≈ 018976224. To estimate the error, note that 1 2 + 5 1 5 , so the remainder term is 8 = ∞ =9 1 2 + 5 ∞ =9 1 5 = 159 1 − 15 = 64 × 10−7 geometric series with = 519 and = 1 5. 38. (a) lim →∞ +1 = lim →∞ ( + 1)+1 [2( + 1)]! · (2)! = lim →∞ ( + 1)( + 1)1 (2 + 2)(2 + 1) = lim →∞ + 1 2(21+ 1) = lim →∞1 + 1 2(21+ 1) = · 0 = 0 1 so the series converges by the Ratio Test. (b) The series in part (a) is convergent, so lim →∞ = lim →∞ (2)! = 0 by Theorem 11.2.6. 39. Use the Limit Comparison Test. lim →∞ + 1 = lim →∞ + 1 = lim →∞1 + 1 = 1 0. Since || is convergent, so is + 1 , by the Limit Comparison Test. 40. lim →∞ +1 = lim →∞ +1 ( + 1)2 5+1 · 25 = lim →∞ 1 (1 + 1)2 || 5 = || 5 , so by the Ratio Test, ∞ =1 (−1) 2 5 converges when || 5 1 ⇔ || 5, so = 5. When = −5, the series becomes the convergent -series ∞ =1 1 2 with = 2 1. When = 5, the series becomes ∞ =1 (−1) 2 , which converges by the Alternating Series Test. Thus, = [−55]. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE CHAPTER 11 REVIEW ¤ 1079 41. lim →∞ +1 = lim →∞(|+ 1) 4 + 2|+1 +1 · |+ 2 4| = lim →∞ + 1 | + 2 4 | = | + 2 4 | 1 ⇔ | + 2| 4, so = 4. | + 2| 4 ⇔ −4 + 2 4 ⇔ −6 2. If = −6, then the series ∞ =1 ( + 2) 4 becomes ∞ =1 (−4) 4 = ∞ =1 (−1) , the alternating harmonic series, which converges by the Alternating Series Test. When = 2, the series becomes the harmonic series ∞ =1 1 , which diverges. Thus, = [−62). 42. lim →∞ +1 = lim →∞ 2+1 ( − 2)+1 ( + 3)! · ( + 2)! 2( − 2) = lim →∞ 2 + 3 | − 2| = 0 1, so the series ∞ =1 2 ( − 2) ( + 2)! converges for all . = ∞ and = (−∞ ∞). 43. lim →∞ +1 = lim →∞ 2+1( − 3)+1 √ + 4 · √ + 3 2( − 3) = 2| − 3| lim →∞ + 3 + 4 = 2| − 3| 1 ⇔ | − 3| 1 2 , so = 1 2 . | − 3| 1 2 ⇔ − 1 2 − 3 1 2 ⇔ 5 2 7 2 . For = 7 2 , the series ∞ =1 2( − 3) √ + 3 becomes ∞ =0 1 √ + 3 = ∞ =3 1 12 , which diverges = 1 2 ≤ 1, but for = 5 2 , we get ∞ =0 (−1) √ + 3, which is a convergent alternating series, so = 5 2 7 2. 44. lim →∞ +1 = lim →∞ (2 + 2)!+1 [( + 1)!]2 · (!)2 (2)! = lim →∞ (2 + 2)(2 + 1) ( + 1)( + 1) || = 4||. To converge, we must have 4|| 1 ⇔ || 1 4 , so = 1 4 . 45. ()() () 6 0 sin 1 2 1 cos √3 2 2 −sin − 1 2 3 −cos − √3 2 4 sin 1 2 ... ... ... sin = 6 + 06 − 6 + 002!6 − 6 2 + (3)3! 6 − 6 3 + (4)4! 6 − 6 4 + · · · = 1 2 1 − 2! 1 − 6 2 + 4! 1 − 6 4 − · · · + √23 − 6 − 3! 1 − 6 3 + · · · = 1 2 ∞ =0 (−1) 1 (2)! − 6 2 + √23 ∞=0 (−1) (2 1+ 1)! − 6 2+1 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1080 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES 46. ()() () 3 0 cos 1 2 1 −sin − √3 2 2 −cos − 1 2 3 sin √3 2 4 cos 1 2 ... ... ... cos = 3 + 03 − 3 + 002!3 − 3 2 + (3)3! 3 − 3 3 + (4)4! 3 − 3 4 + · · · = 1 2 1 − 2! 1 − 3 2 + 4! 1 − 3 4 − · · · + √23 − − 3 + 3! 1 − 3 3 − · · · = 1 2 ∞ =0 (−1) 1 (2)! − 3 2 + √23 ∞=0 (−1)+1 (2 1+ 1)! − 3 2+1 47. 1 1 + = 1 1 − (−) = ∞ =0 (−) = ∞ =0 (−1) for || 1 ⇒ 2 1 + = ∞ =0 (−1) +2 with = 1. 48. tan−1 = ∞ =0 (−1) 2+1 2 + 1 with interval of convergence [−11], so tan−1(2) = ∞ =0 (−1) (2)2+1 2 + 1 = ∞ =0 (−1) 4+2 2 + 1 , which converges when 2 ∈ [−1 1] ⇔ ∈ [−1 1]. Therefore, = 1. 49. 4 −1 = −ln(4 − ) + and 4 −1 = 14 1 −14 = 1 4 ∞=0 4 = 14 ∞=0 4 = 14 ∞=0 4(+1 + 1) + . So ln(4 − ) = −1 4 ∞ =0 +1 4( + 1) + = − ∞ =0 +1 4+1( + 1) + = − ∞ =1 4 + . Putting = 0, we get = ln 4. Thus, () = ln(4 − ) = ln 4 − ∞ =1 4 . The series converges for |4| 1 ⇔ || 4, so = 4. Another solution: ln(4 − ) = ln[4(1 − 4)] = ln4 + ln(1 − 4) = ln4 + ln[1 + (−4)] = ln4 + ∞ =1 (−1)+1 (−4) [from Table 1] = ln4 + ∞ =1 (−1)2+1 4 = ln4 − ∞ =1 4 . 50. = ∞ =0 ! ⇒ 2 = ∞ =0 (2) ! ⇒ 2 = ∞ =0 2 ! = ∞ =0 2 +1 ! , = ∞ 51. sin = ∞ =0 (−1) 2+1 (2 + 1)! ⇒ sin(4) = ∞ =0 (−1) (4)2+1 (2 + 1)! = ∞ =0 (−1) 8+4 (2 + 1)! for all , so the radius of convergence is ∞. 52. = ∞ =0 ! ⇒ 10 = (ln 10) = ∞ =0 [(ln10)] ! = ∞ =0 (ln10) ! , = ∞ °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE CHAPTER 11 REVIEW ¤ 1081 53. () = √4 161− = 4 16(11− 16) = √4 161 −1 16 1 14 = 1 21 − 16 1 −14 = 1 2 1 + −14−16 + − 1 4 2!− 5 4−16 2 + − 1 4 −3!5 4 − 9 4−16 3 + · · · = 1 2 + ∞ =1 1 · 5 · 9 · · · · · (4 − 3) 2 · 4 · ! · 16 = 12 + ∞ =1 1 · 5 · 9 · · · · · (4 − 3) 26+1 ! for − 16 1 ⇔ || 16, so = 16. 54. (1 − 3)−5 = ∞ =0 −5(−3) = 1 + (−5)(−3) + (−5)( 2!−6) (−3)2 + (−5)(−3!6)(−7) (−3)3 + · · · = 1 + ∞ =1 5 · 6 · 7 · · · · · ( + 4) · 3 ! for |−3| 1 ⇔ || 1 3, so = 1 3. 55. = ∞ =0 ! , so = 1 ∞ =0 ! = ∞ =0 −1 ! = −1 + ∞ =1 −1 ! = 1 + ∞ =1 −1 ! and = + ln|| + ∞=1 ·!. 56. (1 + 4)12 = ∞ =0 1 2(4) = 1 + 1 24 + 1 22!− 1 2 (4)2 + 1 2−3! 1 2− 3 2 (4)3 + · · · = 1 + 1 2 4 − 1 8 8 + 16 1 12 − · · · so 01(1 + 4)12 = + 10 1 5 − 72 1 9 + 208 1 13 − · · · 1 0 = 1 + 10 1 − 72 1 + 208 1 − · · · . This is an alternating series, so by the Alternating Series Test, the error in the approximation 01(1 + 4)12 ≈ 1 + 10 1 − 72 1 ≈ 1086 is less than 208 1 , sufficient for the desired accuracy. Thus, correct to two decimal places, 01(1 + 4)12 ≈ 109. 57. (a) ()() ()(1) 0 12 1 1 1 2 −12 1 2 2 − 1 4 −32 − 1 4 3 3 8 −52 3 8 4 − 15 16 −72 − 15 16 ... ... ... √ ≈ 3() = 1 + 12 1! ( − 1) − 12! 4 ( − 1)2 + 33! 8 ( − 1)3 = 1 + 1 2( − 1) − 1 8( − 1)2 + 16 1 ( − 1)3 (b) (c) |3 ()| ≤ 4! | − 1|4, where (4) () ≤ with (4)() = − 15 16 −72. Now 09 ≤ ≤ 11 ⇒ −01 ≤ − 1 ≤ 01 ⇒ ( − 1)4 ≤ (01)4, and letting = 09 gives = 15 16(09)72 , so |3()| ≤ 15 16(09)72 4! (01)4 ≈ 0000 005 648 ≈ 0000 006 = 6 × 10−6. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1082 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES (d) From the graph of |3()| = |√ − 3()|, it appears that the error is less than 5 × 10−6 on [0911]. 58. (a) ()() ()(0) 0 sec 1 1 sectan 0 2 sectan2 + sec3 1 3 sectan3 + 5 sec3 tan 0 ... ... ... sec ≈ 2() = 1 + 1 22 (b) (c) |2 ()| ≤ 3! ||3, where (3)() ≤ with (3)() = sec tan3 + 5 sec3 tan. Now 0 ≤ ≤ 6 ⇒ 3 ≤ 6 3, and letting = 6 gives = 14 3 , so |2 ()| ≤ 314 · 6 6 3 ≈ 0111648. (d) From the graph of |2()| = |sec − 2()|, it appears that the error is less than 002 on 0 6 . 59. sin = ∞ =0 (−1) 2+1 (2 + 1)! = − 3 3! + 5 5! − 7 7! + · · · , so sin − = −3! 3 + 5! 5 − 7! 7 + · · · and sin − 3 = − 1 3! + 2 5! − 4 7! + · · · . Thus, lim →0 sin3− = lim →0 −16 + 120 2 − 5040 4 + · · · = −1 6. 60. (a) = 2 ( + )2 = (1 + )2 = ∞ =0 −2 [binomial series] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE CHAPTER 11 REVIEW ¤ 1083 (b) We expand = 1 − 2() + 3 ()2 − · · · . This is an alternating series, so by the Alternating Series Estimation Theorem, the error in the approximation = is less than 2, so for accuracy within 1% we want 2 2( + )2 001 ⇔ 2( + )2 3 001. This inequality would be difficult to solve for , so we substitute = 6,400 km and plot both sides of the inequality. It appears that the approximation is accurate to within 1% for 31 km. 61. () = ∞ =0 ⇒ (−) = ∞ =0 (−) = ∞ =0 (−1) (a) If is an odd function, then (−) = −() ⇒ ∞ =0 (−1) = ∞ =0 −. The coefficients of any power series are uniquely determined (by Theorem 11.10.5), so (−1) = −. If is even, then (−1) = 1, so = − ⇒ 2 = 0 ⇒ = 0. Thus, all even coefficients are 0, that is, 0 = 2 = 4 = · · · = 0. (b) If is even, then (−) = () ⇒ ∞ =0 (−1) = ∞ =0 ⇒ (−1) = . If is odd, then (−1) = −1, so − = ⇒ 2 = 0 ⇒ = 0. Thus, all odd coefficients are 0, that is, 1 = 3 = 5 = · · · = 0. 62. = ∞ =0 ! ⇒ () = 2 = ∞ =0 (2) ! = ∞ =0 2 ! = ∞ =0 1 ! 2. By Theorem 11.10.6 with = 0, we also have () = ∞ =0 ()(0) ! . Comparing coefficients for = 2, we have (2 (2))! (0) = 1! ⇒ (2)(0) = (2!)!. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1084 ¤ CHAPTER 11 INFINITE SEQUENCES AND SERIES °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE PROBLEMS PLUS 1. It would be far too much work to compute 15 derivatives of . The key idea is to remember that ()(0) occurs in the coefficient of in the Maclaurin series of . We start with the Maclaurin series for sin: sin = − 3 3! + 5 5! − · · · . Then sin(3) = 3 − 9 3! + 15 5! − · · · , and so the coefficient of 15 is (15) 15!(0) = 5! 1 . Therefore, (15)(0) = 15! 5! = 6 · 7 · 8 · 9 · 10 · 11 · 12 · 13 · 14 · 15 = 10,897,286,400. 2. We use the problem-solving strategy of taking cases: Case (i): If || 1, then 0 ≤ 2 1, so lim →∞ 2 = 0 [see Example 11.1.11] and () = lim →∞ 2 − 1 2 + 1 = 0 − 1 0 + 1 = −1.[] Case (ii): If || = 1, that is, = ±1, then 2 = 1, so () = lim →∞ 2 − 1 2 + 1 = lim →∞ 1 1 + 1 − 1 = 0. Case (iii): If || 1, then 2 1, so lim →∞ 2 = ∞ and () = lim →∞ 2 − 1 2 + 1 = lim →∞ 1 1 + (1 − (1 2 2 ) ) = 1 1 + 0 − 0 = 1. Thus, () = 1 if −1 0 if = −1 −1 if −1 1 0 if = 1 1 if 1 The graph shows that is continuous everywhere except at = ±1. 3. (a) From Formula 14a in Appendix D, with = = , we get tan 2 = 2tan 1 − tan2 , so cot 2 = 1 −2tan tan2 ⇒ 2cot 2 = 1 − tan2 tan = cot − tan. Replacing by 1 2 , we get 2cot = cot 1 2 − tan 1 2 , or tan 1 2 = cot 1 2 − 2cot. (b) From part (a) with 2−1 in place of , tan 2 = cot 2 − 2cot 2−1 , so the th partial sum of ∞ =1 1 2 tan 2 is = tan(2) 2 + tan(4) 4 + tan(8) 8 + · · · + tan(2) 2 = cot(22) − cot + cot(44) − cot(22) + cot(88) − cot(44) + · · · +cot(2 2) − cot(2 −21−1) = −cot + cot(2 2) [telescoping sum] Now cot(2) 2 = cos(2) 2 sin(2) = cos(2) · 2 sin(2) → 1 · 1 = 1 as → ∞ since 2 → 0 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. 1085 FOR INSTRUCTOR USE ONLYNOT FOR SALE 1086 ¤ CHAPTER 11 PROBLEMS PLUS for 6= 0. Therefore, if 6= 0 and 6= where is any integer, then ∞ =1 1 2 tan 2 = lim →∞ = lim →∞−cot + 21 cot 2 = −cot + 1 If = 0, then all terms in the series are 0, so the sum is 0. 4. |2|2 = 2, |3|2 = 2 + 22, |4|2 = 2 + 22 + 222, |5|2 = 2 + 22 + 222 + 232, , ||2 = 2 + 22 + 222 + ··· + (2−2)2 [for ≥ 3] = 2 + (4 + 42 + 43 + ·· · + 4−2) = 2 + 4(4−2 − 1) 4 − 1 [finite geometric sum with = 4, = 4] = 6 3 + 4−13− 4 = 2 3 + 43−1 So tan∠+1 = |+1| || = 2−1 2 3 + 43−1 = √4−1 2 3 + 43−1 = 1 3 · 42−1 + 1 3 → √3 as → ∞. Thus, ∠+1 → 3 as → ∞. 5. (a) At each stage, each side is replaced by four shorter sides, each of length 1 3 of the side length at the preceding stage. Writing 0 and 0 for the number of sides and the length of the side of the initial triangle, we generate the table at right. In general, we have = 3 · 4 and = 1 3, so the length of the perimeter at the th stage of construction is = = 3 · 4 · 1 3 = 3 · 4 3. 0 = 3 0 = 1 1 = 3 · 4 1 = 13 2 = 3 · 42 2 = 132 3 = 3 · 43 3 = 133 ... ... (b) = 4 3−1 = 443−1. Since 4 3 1, → ∞ as → ∞. (c) The area of each of the small triangles added at a given stage is one-ninth of the area of the triangle added at the preceding stage. Let be the area of the original triangle. Then the area of each of the small triangles added at stage is = · 1 9 = 9 . Since a small triangle is added to each side at every stage, it follows that the total area added to the figure at the th stage is = −1 · = 3 · 4−1 · 9 = · 4−1 32−1 . Then the total area enclosed by the snowflake curve is = + 1 + 2 + 3 + ·· · = + · 1 3 + · 4 33 + · 42 35 + · 43 37 + ···. After the first term, this is a geometric series with common ratio 4 9 , so = + 3 1 − 4 9 = + 3 · 9 5 = 8 5 . But the area of the original equilateral triangle with side 1 is = 1 2 · 1 · sin 3 = √3 4 . So the area enclosed by the snowflake curve is 85 · √43 = 2√5 3. 6. Let the series = 1 + 1 2 + 1 3 + 1 4 + 1 6 + 1 8 + 1 9 + 12 1 + ·· ·. Then every term in is of the form 213 , , ≥ 0, and furthermore each term occurs only once. So we can write = ∞ =0 ∞ =0 1 23 = ∞ =0 ∞ =0 1 2 1 3 = ∞ =0 1 2 ∞ =0 1 3 = 1 1 − 1 2 · 1 1 − 1 3 = 2 · 3 2 = 3 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE CHAPTER 11 PROBLEMS PLUS ¤ 1087 7. (a) Let = arctan and = arctan. Then, from Formula 14b in Appendix D, tan( − ) = tan − tan 1 + tan tan = tan(arctan) − tan(arctan) 1 + tan(arctan) tan(arctan) = − 1 + Now arctan − arctan = − = arctan(tan( − )) = arctan − 1 + since − 2 − 2 . (b) From part (a) we have arctan 120 119 − arctan 239 1 = arctan 120 119 − 1 239 1 + 120 119 · 1 239 = arctan 28,561 28,441 28,561 28,441 = arctan 1 = 4 (c) Replacing by − in the formula of part (a), we get arctan + arctan = arctan + 1 − . So 4arctan 1 5 = 2arctan 1 5 + arctan 1 5 = 2 arctan 1 5 + 1 5 1 − 1 5 · 1 5 = 2 arctan 5 12 = arctan 12 5 + arctan 12 5 = arctan 5 12 + 12 5 1 − 5 12 · 5 12 = arctan 120 119 Thus, from part (b), we have 4arctan 1 5 − arctan 239 1 = arctan 120 119 − arctan 239 1 = 4 . (d) From Example 7 in Section 11.9 we have arctan = − 3 3 + 5 5 − 7 7 + 9 9 − 11 11 + · · · , so arctan 1 5 = 1 5 − 1 3 · 53 + 1 5 · 55 − 1 7 · 57 + 1 9 · 59 − 1 11 · 511 + · · · This is an alternating series and the size of the terms decreases to 0, so by the Alternating Series Estimation Theorem, the sum lies between 5 and 6, that is, 0197395560 arctan 1 5 0197395562. (e) From the series in part (d) we get arctan 1 239 = 1 239 − 1 3 · 2393 + 1 5 · 2395 − · · · . The third term is less than 26 × 10−13, so by the Alternating Series Estimation Theorem, we have, to nine decimal places, arctan 1 239 ≈ 2 ≈ 0004184076. Thus, 0004184075 arctan 239 1 0004184077. (f) From part (c) we have = 16 arctan 1 5 − 4arctan 239 1 , so from parts (d) and (e) we have 16(0197395560) − 4(0004184077) 16(0197395562) − 4(0004184075) ⇒ 3141592652 3141592692. So, to 7 decimal places, ≈ 31415927. 8. (a) Let = arccot and = arccot where 0 − . Then cot( − ) = 1 tan( − ) = 1 + tan tan tan − tan = 1 cot · 1 cot + 1 1 cot − 1 cot · cot cot cot cot = 1 + cot cot cot − cot = 1 + cot(arccot) cot(arccot) cot(arccot ) − cot(arccot) = 1 + − Now arccot − arccot = − = arccot(cot( − )) = arccot 1 + − since 0 − . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1088 ¤ CHAPTER 11 PROBLEMS PLUS (b) From part (a), we want arccot(2 + + 1) to equal arccot 1 + − . Note that 1 + = 2 + + 1 ⇔ = 2 + = ( + 1), so if we let = + 1 and = , then − = 1. Therefore, arccot(2 + + 1) = arccot(1 + ( + 1)) = arccot 1 + ( + 1) ( + 1) − = arccot − arccot( + 1) Thus, we have a telescoping series with th partial sum = [arccot 0 − arccot 1] + [arccot 1 − arccot 2] + · · · + [arccot − arccot( + 1)] = arccot 0 − arccot( + 1). Thus, ∞ =0 arccot(2 + + 1) = lim →∞ = lim →∞ [arccot 0 − arccot( + 1)] = 2 − 0 = 2 . 9. We want arctan22 to equal arctan 1 + − . Note that 1 + = 2 ⇔ = 2 − 1 = ( + 1)( − 1), so if we let = + 1 and = − 1, then − = 2 and 6= −1. Thus, from Problem 7(a), arctan22 = arctan 1 + − = arctan − arctan = arctan( + 1) − arctan( − 1). Therefore, =1 arctan22 = =1 [arctan( + 1) − arctan( − 1)] = =1 [arctan( + 1) − arctan + arctan − arctan( − 1)] = =1 [arctan( + 1) − arctan] + =1 [arctan − arctan( − 1)] = [arctan( + 1) − arctan 1] + [arctan − arctan 0] [since both sums are telescoping] = arctan( + 1) − 4 + arctan − 0 Now =1 arctan22 = lim →0 =1 arctan22 = lim →∞arctan( + 1) − 4 + arctan = 2 − 4 + 2 = 34 . Note: For all ≥ 1, 0 ≤ arctan( − 1) arctan( + 1) 2 , so − 2 arctan( + 1) − arctan( − 1) 2 , and the identity in Problem 7(a) holds. 10. Let’s first try the case = 1: 0 + 1 = 0 ⇒ 1 = −0 ⇒ lim →∞ 0√ + 1√ + 1 = lim →∞ 0√ − 0√ + 1 = 0 lim →∞ √ − √ + 1 √ + √ + 1 √ + √ + 1 = 0 lim →∞ −1 √ + √ + 1 = 0 In general we have 0 + 1 + · · · + = 0 ⇒ = −0 − 1 − · · · − −1 ⇒ lim →∞ 0√ + 1√ + 1 + 2√ + 2 + · · · + √ + = lim →∞ 0√ + 1√ + 1 + · · · + −1√ + − 1 − 0√ + − 1√ + − · · · − −1√ + = 0 lim →∞ √ − √ + + 1 lim →∞ √ + 1 − √ + + · · · + −1 lim →∞ √ + − 1 − √ + Each of these limits is 0 by the same type of simplification as in the case = 1. So we have lim →∞ 0√ + 1√ + 1 + 2√ + 2 + · · · + √ + = 0(0) + 1(0) + · · · + −1(0) = 0 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE CHAPTER 11 PROBLEMS PLUS ¤ 1089 11. We start with the geometric series ∞ =0 = 1 1 − , || 1, and differentiate: ∞ =1 −1 = ∞=0 = 1 −1 = (1 −1)2 for || 1 ⇒ ∞=1 = ∞=1 −1 = (1 −)2 for || 1. Differentiate again: ∞ =1 2−1 = (1 − )2 = (1 − )2 − · 2(1 − )(−1) (1 − )4 = + 1 (1 − )3 ⇒ ∞ =1 2 = 2 + (1 − )3 ⇒ ∞ =1 3−1 = 2 + (1 − )3 = (1 − )3(2 + 1) − (2 + )3(1 − )2(−1) (1 − )6 = 2 + 4 + 1 (1 − )4 ⇒ ∞ =1 3 = 3 + 42 + (1 − )4 , || 1. The radius of convergence is 1 because that is the radius of convergence for the geometric series we started with. If = ±1, the series is 3(±1), which diverges by the Test For Divergence, so the interval of convergence is (−11). 12. Place the -axis as shown and let the length of each book be . We want to show that the center of mass of the system of books lies above the table, that is, . The -coordinates of the centers of mass of the books are 1 = 2 , 2 = 2( − 1) + 2 , 3 = 2( − 1) + 2( − 2) + 2 , and so on. Each book has the same mass , so if there are books, then = 1 + 2 + · · · + = 1 + 2 + · · · + = 1 2 + 2(− 1) + 2 + 2(− 1) + 2(− 2) + 2 + · · · + 2(− 1) + 2(− 2) + · · · + 4 + 2 + 2 = 2(−−11) + 2(−−22) + · · · + 2 4 + 1 2 + 2 = ( − 1) 12 + 2 = 22− 1 This shows that, no matter how many books are added according to the given scheme, the center of mass lies above the table. It remains to observe that the series 1 2 + 1 4 + 1 6 + 1 8 + · · · = 1 2 (1) is divergent (harmonic series), so we can make the top book extend as far as we like beyond the edge of the table if we add enough books. 13. ln1 − 12 = ln2−2 1 = ln ( + 1)( 2 − 1) = ln[( + 1)( − 1)] − ln2 = ln( + 1) + ln( − 1) − 2ln = ln( − 1) − ln − ln + ln( + 1) = ln − 1 − [ln − ln( + 1)] = ln − 1 − ln + 1 . Let = =2 ln1 − 12 = =2 ln − 1 − ln + 1 for ≥ 2. Then °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1090 ¤ CHAPTER 11 PROBLEMS PLUS = ln 12 − ln 23 + ln 23 − ln 34 + · · · + ln − 1 − ln + 1 = ln 12 − ln + 1 , so ∞ =2 ln1 − 12 = lim →∞ = lim →∞ln 12 − ln + 1 = ln 12 − ln1 = ln1 − ln2 − ln1 = −ln2 (or ln 1 2 ). 14. First notice that both series are absolutely convergent (p-series with 1.) Let the given expression be called . Then = 1 + 1 2 + 1 3 + 1 4 + · · · 1 − 1 2 + 1 3 − 1 4 + · · · = 1 + 2 · 21 − 21 + 31 + 2 · 41 − 41 + · · · 1 − 1 2 + 1 3 − 1 4 + · · · = 1 − 21 + 31 − 41 + · · · + 2 · 21 + 2 · 41 + 2 · 61 + · · · 1 − 1 2 + 1 3 − 1 4 + · · · = 1 + 221 + 41 + 61 + 81 + · · · 1 − 1 2 + 1 3 − 1 4 + · · · = 1 + 1 2−1 1 + 21 + 31 + 41 + · · · 1 − 1 2 + 1 3 − 1 4 + · · · = 1 + 21− Therefore, = 1 + 21− ⇔ − 21− = 1 ⇔ (1 − 21−) = 1 ⇔ = 1 1 − 21− . 15. If is the length of a side of the equilateral triangle, then the area is = 1 2 · √23 = √43 2 and so 2 = √43 . Let be the radius of one of the circles. When there are rows of circles, the figure shows that = √3 + + ( − 2)(2) + + √3 = 2 − 2 + 2√3, so = 2 + √3 − 1. The number of circles is 1 + 2 + · · · + = ( + 1) 2 , and so the total area of the circles is = ( + 1) 2 2 = ( + 1) 2 2 4 + √3 − 12 = ( + 1) 2 4√3 4 + √3 − 12 = ( + 1) + √3 − 12 2√3 ⇒ = ( + 1) + √3 − 12 2√3 = 1 + 1 1 + √3 − 12 2√3 → 2√3 as → ∞ 16. Given 0 = 1 = 1 and = ( − 1)( − 2)−1 − ( − 3)−2 ( − 1) , we calculate the next few terms of the sequence: 2 = 1 · 0 · 1 − (−1)0 2 · 1 = 1 2 , 3 = 2 · 1 · 2 − 0 · 1 3 · 2 = 1 6 , 4 = 3 · 2 · 3 − 1 · 2 4 · 3 = 1 24. It seems that = 1!, so we try to prove this by induction. The first step is done, so assume = 1 ! and −1 = ( −1 1)!. Then °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE CHAPTER 11 PROBLEMS PLUS ¤ 1091 +1 = ( − 1) − ( − 2)−1 ( + 1) = ( − 1) ! − − 2 ( − 1)! ( + 1) = ( − 1) − ( − 2) [( + 1)()]( − 1)! = 1 ( + 1)! and the induction is complete. Therefore, ∞ =0 = ∞ =0 1 ! = . 17. (a) The x-intercepts of the curve occur where sin = 0 ⇔ = , an integer. So using the formula for disks (and either a CAS or sin2 = 1 2(1 − cos2) and Formula 99 to evaluate the integral), the volume of the nth bead is = ( −1)(−10 sin)2 = ( −1) −5 sin2 = 250 101 (−(−1)5 − −5) (b) The total volume is 0∞ −5 sin2 = ∞ =1 = 250 101 ∞ =1 [−(−1)5 − −5] = 250 101 [telescoping sum]. Another method: If the volume in part (a) has been written as = 250 101 −5(5 − 1), then we recognize ∞ =1 as a geometric series with = 250 101(1 − −5) and = −5 18. (a) Since is defined as the midpoint of −4−3, = 1 2(−4 + −3) for ≥ 5. So we prove by induction that 1 2 + +1 + +2 + +3 = 2. The case = 1 is immediate, since 1 2 · 0 + 1 + 1 + 0 = 2. Assume that the result holds for = − 1, that is, 1 2−1 + + +1 + +2 = 2. Then for = , 1 2 + +1 + +2 + +3 = 1 2 + +1 + +2 + 1 2(+3−4 + +3−3) [by above] = 1 2 −1 + + +1 + +2 = 2 [by the induction hypothesis] Similarly, for ≥ 5, = 1 2(−4 + −3), so the same argument as above holds for , with 2 replaced by 1 2 1 + 2 + 3 + 4 = 1 2 · 1 + 1 + 0 + 0 = 3 2 . So 1 2 + +1 + +2 + +3 = 3 2 for all . (b) lim →∞ 1 2 + +1 + +2 + +3 = 1 2 lim →∞ + lim →∞ +1 + lim →∞ +2 + lim →∞ +3 = 2. Since all the limits on the left hand side are the same, we get 7 2 lim →∞ = 2 ⇒ lim →∞ = 4 7 . In the same way, 7 2 lim →∞ = 3 2 ⇒ lim →∞ = 3 7 , so = 4 7 3 7. 19. By Table 1 in Section 11.10, tan−1 = ∞ =0 (−1) 2+1 2 + 1 for || 1. In particular, for = √13, we have 6 = tan−1√13 = ∞=0(−1) 12√3+ 1 2+1 = ∞=0(−1) 1 3 √13 21+ 1, so = 6 √3 ∞ =0 (−1) (2 + 1)3 = 2√3 ∞ =0 (−1) (2 + 1)3 = 2√31 + ∞=1 (2(−+ 1)3 1) ⇒ ∞=1 (2(−+ 1)3 1) = 2√ 3 − 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1092 ¤ CHAPTER 11 PROBLEMS PLUS 20. (a) Using = + + 2 + · · · + −1 = (1 − ) 1 − , 1 − + 2 − 3 + · · · + 2−2 − 2−1 = 11 − (−)2 1 − (−) = 1 − 2 1 + . (b) 01(1 − + 2 − 3 + · · · + 2−2 − 2−1) = 01 11 + − 2 ⇒ − 22 + 33 − 44 + · · · + 22−−11 − 22 1 0 = 01 1 + − 01 1 + 2 ⇒ 1 − 1 2 + 1 3 − 1 4 + · · · + 1 2 − 1 − 1 2 = 01 1 + − 01 1 + 2 (c) Since 1 − 1 2 = 1 1 · 2, 1 3 − 1 4 = 1 3 · 4 · · · 1 2 − 1 − 1 2 = 1 (2 − 1)(2), we see from part (b) that 1 1 · 2 + 1 3 · 4 + · · · + 1 (2 − 1)(2) − 01 1 + = − 01 1 + 2 . Thus, 1 1 · 2 + 1 3 · 4 + · · · + 1 (2 − 1)(2) − 01 1 + = 01 1 + 2 01 2 since 1 + 2 2 for 0 ≤ 1. (d) Note that 01 1 + = ln(1 + )1 0 = ln 2 and 01 2 = 22+ 1 +1 1 0 = 21+ 1. So part (c) becomes 1 1 · 2 + 1 3 · 4 + · · · + 1 (2 − 1)(2) − ln 2 1 2 + 1 . In other words, the th partial sum of the given series satisfies | − ln 2| 1 2 + 1 . Thus, lim →∞ = ln 2, that is, 1 1 · 2 + 1 3 · 4 + 1 5 · 6 + 1 7 · 8 + · · · = ln 2. 21. Let () denote the left-hand side of the equation 1 + 2! + 2 4! + 3 6! + 4 8! + · · · = 0. If ≥ 0, then () ≥ 1 and there are no solutions of the equation. Note that (−2) = 1 − 2 2! + 4 4! − 6 6! + 8 8! − · · · = cos. The solutions of cos = 0 for 0 are given by = 2 − , where is a positive integer. Thus, the solutions of () = 0 are = − 2 − 2, where is a positive integer. 22. Suppose the base of the first right triangle has length . Then by repeated use of the Pythagorean theorem, we find that the base of the second right triangle has length √1 + 2, the base of the third right triangle has length √2 + 2, and in general, the nth right triangle has base of length √ − 1 + 2 and hypotenuse of length √ + 2. Thus, = tan−11√ − 1 + 2 and ∞ =1 = ∞ =1 tan−1√ −11 + 2 = ∞=0tan−1√1+ 2 . We wish to show that this series diverges. First notice that the series ∞ =1 1 √ + 2 diverges by the Limit Comparison Test with the divergent p-series ∞ =1 1 √ = 1 2 ≤ 1 since lim →∞ 1√ + 2 1√ = lim →∞ √ √ + 2 = lim →∞ +2 = lim →∞ 1 +12 = 1 0. Thus, °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE CHAPTER 11 PROBLEMS PLUS ¤ 1093 ∞ =0 1 √ + 2 also diverges. Now ∞ =0 tan−1√1+ 2 diverges by the Limit Comparison Test with ∞=0 √1+ 2 since lim →∞ tan−11√ + 2 1√ + 2 = lim →∞ tan−11√ + 2 1√ + 2 = lim →∞ tan−11 (1) = √ + 2 = lim →0+ tan−1 = 1 = lim H →0+ 1(1 + 2) 1 = 1 0 Thus, ∞ =1 is a divergent series. 23. Call the series . We group the terms according to the number of digits in their denominators: = 1 1 + 1 2 + · · · + 1 8 + 1 9 1 + 11 1 + · · · + 99 1 2 + 111 1 + · · · + 999 1 3 + · · · Now in the group , since we have 9 choices for each of the digits in the denominator, there are 9 terms. Furthermore, each term in is less than 101−1 [except for the first term in 1]. So 9 · 101−1 = 9 10 9 −1. Now ∞ =1 9 10 9 −1 is a geometric series with = 9 and = 10 9 1. Therefore, by the Comparison Test, = ∞ =1 ∞ =1 9 10 9 −1 = 1 −9910 = 90. 24. (a) Let () = 1 − − 2 = ∞ =0 = 0 + 1 + 22 + 33 + · · · . Then = (1 − − 2)(0 + 1 + 22 + 33 + · · ·) = 0 + 1 + 22 + 33 + 44 + 55 + · · · − 0 − 12 − 23 − 34 − 45 − · · · − 02 − 13 − 24 − 35 − · · · = 0 + (1 − 0) + (2 − 1 − 0)2 + (3 − 2 − 1)3 + · · · Comparing coefficients of powers of gives us 0 = 0 and 1 − 0 = 1 ⇒ 1 = 0 + 1 = 1 2 − 1 − 0 = 0 ⇒ 2 = 1 + 0 = 1 + 0 = 1 3 − 2 − 1 = 0 ⇒ 3 = 2 + 1 = 1 + 1 = 2 In general, we have = −1 + −2 for ≥ 3. Each is equal to the th Fibonacci number, that is, ∞ =0 = ∞ =1 = ∞ =1 (b) Completing the square on 2 + − 1 gives us 2 + + 14 − 1 − 14 = + 122 − 5 4 = + 122 − √25 2 = + 12 + √25 + 1 2 − √25 = + 1 +2√5 + 1 −2√5 [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1094 ¤ CHAPTER 11 PROBLEMS PLUS So 1 − − 2 = − 2 + − 1 = − + 1 +2√5 + 1−2√5. The factors in the denominator are linear, so the partial fraction decomposition is − + 1 +2√5 + 1 −2√5 = + 1 +√5 2 + + 1− √5 2 − = + 1−2√5 + + 1 +2√5 If = −1 +√5 2 , then − −1 +2 √5 = √5 ⇒ = 12−√√55. If = −1− √5 2 , then − −1 −2 √5 = −√5 ⇒ = 1 + −2√√55. Thus, 1 − − 2 = 1 + √5 −2√5 + 1 + √5 2 + 1 − √5 2√5 + 1 − √5 2 = 1 + √5 −2√5 + 1 + √5 2 · 2 1 + √5 2 1 + √5 + 1 − √5 2√5 + 1 − √5 2 · 2 1 − √5 2 1 − √5 = −1√5 1 + 2 1 + √5 + 1√5 1 + 2 1 − √5 = − 1 √ 5 ∞ =0−1 +2√5 + √15 ∞=0−1 −2√5 = 1 √ 5 ∞ =01 −−2√5 − 1 +−2√5 = 1 √ 5 ∞ =1(−2)1 + 1 −√√55−1 + (−2) √51 − √5 [the = 0 term is 0] = 1 √ 5 ∞ =1 (−2)1 + √5 − 1 − √5 (1 − 5) = 1 √ 5 ∞ =1 1 + √52−1 − √5 [(−4) = (−2) · 2] From part (a), this series must equal ∞ =1 , so = 1 + √5 − 1 − √5 2√5 , which is an explicit formula for the nth Fibonacci number. 25. = 1 + 3 3! + 6 6! + 9 9! + · · · , = + 4 4! + 7 7! + 10 10! + · · · , = 2 2! + 5 5! + 8 8! + · · · . Use the Ratio Test to show that the series for , , and have positive radii of convergence (∞ in each case), so Theorem 11.9.2 applies, and hence, we may differentiate each of these series: = 32 3! + 65 6! + 98 9! + · · · = 2 2! + 5 5! + 8 8! + · · · = Similarly, = 1 + 3! 3 + 6! 6 + 9! 9 + · · · = , and = + 4! 4 + 7! 7 + 10! 10 + · · · = . So 0 = , 0 = , and 0 = . Now differentiate the left-hand side of the desired equation: (3 + 3 + 3 − 3) = 320 + 320 + 320 − 3(0 + 0 + 0) = 32 + 32 + 32 − 3(2 + 2 + 2) = 0 ⇒ °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE CHAPTER 11 PROBLEMS PLUS ¤ 1095 3 + 3 + 3 − 3 = . To find the value of the constant , we put = 0 in the last equation and get 13 + 03 + 03 − 3(1 · 0 · 0) = ⇒ = 1, so 3 + 3 + 3 − 3 = 1. 26. To prove: If 1, then the nth partial sum = =1 1 of the harmonic series is not an integer. Proof: Let 2 be the largest power of 2 that is less than or equal to and let be the product of all the odd positive integers that are less than or equal to . Suppose that = , an integer. Then 2 = 2. Since ≥ 2, we have ≥ 1, and hence, 2 is an even integer. We will show that 2 is an odd integer, contradicting the equality 2 = 2 and showing that the supposition that is an integer must have been wrong. 2 = 2 =1 1 = =1 2 . If 1 ≤ ≤ and is odd, then is an odd integer since is one of the odd integers that were multiplied together to form . Thus, 2 is an even integer in this case. If 1 ≤ ≤ and is even, then we can write = 2, where 2 is the largest power of 2 dividing and is odd. If , then 2 = 2 2 · = 2− , which is an even integer, the product of the even integer 2− and the odd integer . If = , then = 1, since 1 = ≥ 2 ⇒ = 2 ≥ 2 · 2 = 2+1, contrary to the choice of 2 as the largest power of 2 that is less than or equal to . This shows that = only when = 2. In that case, 2 = , an odd integer. Since 2 is an even integer for every except 2 and 2 is an odd integer when = 2, we see that 2 is an odd integer. This concludes the proof. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLYNOT FOR SALE 1096 ¤ CHAPTER 11 PROBLEMS PLUS °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. FOR INSTRUCTOR USE ONLY [Show More]
Last updated: 3 years ago
Preview 1 out of 2 pages

Buy this document to get the full access instantly
Instant Download Access after purchase
Buy NowInstant download
We Accept:

Reviews( 0 )
$10.00
Can't find what you want? Try our AI powered Search
Document information
Connected school, study & course
About the document
Uploaded On
Jan 06, 2020
Number of pages
2
Written in
All
Additional information
This document has been written for:
Uploaded
Jan 06, 2020
Downloads
0
Views
107


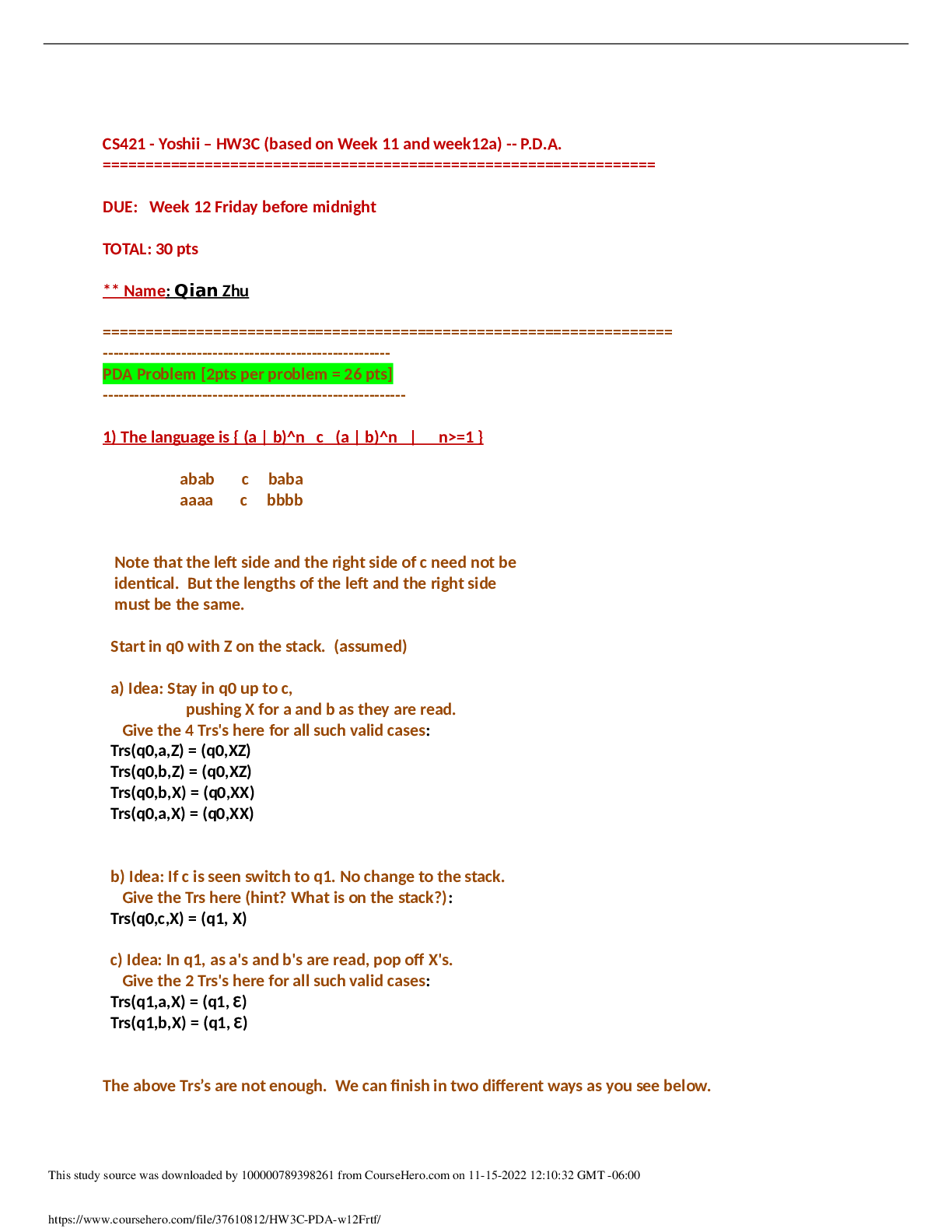


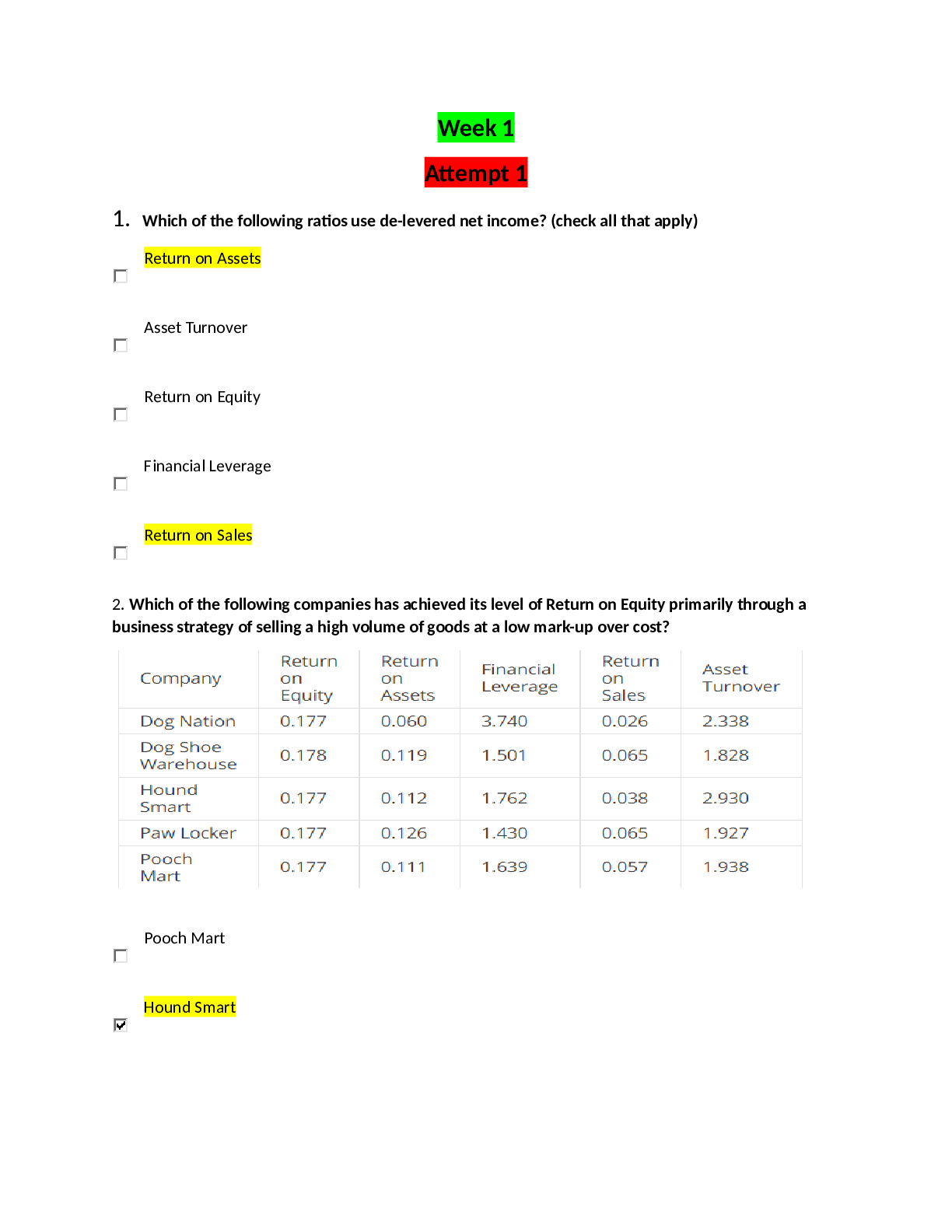
.png)
.png)
.png)
.png)
.png)
.png)
.png)