16.1 Vector Fields
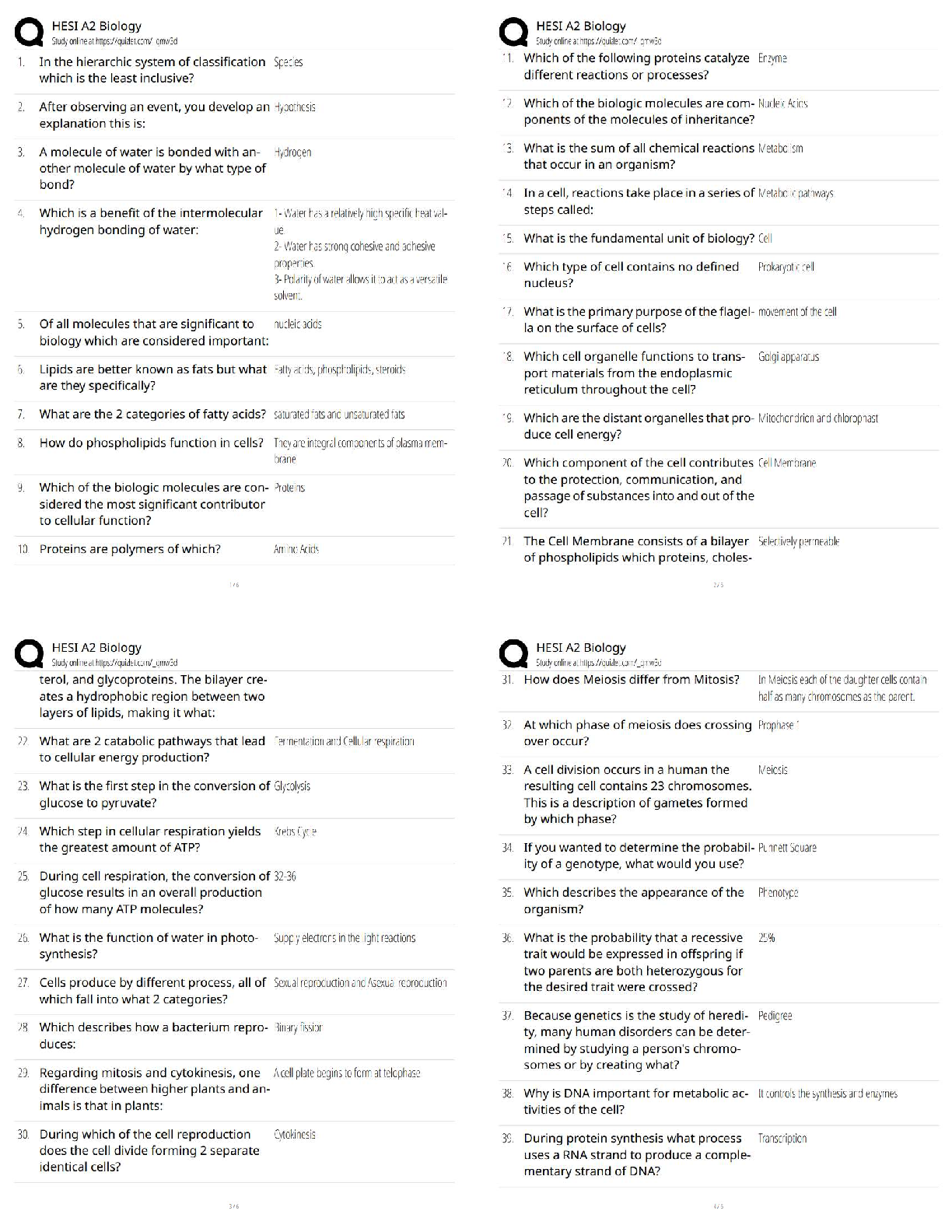
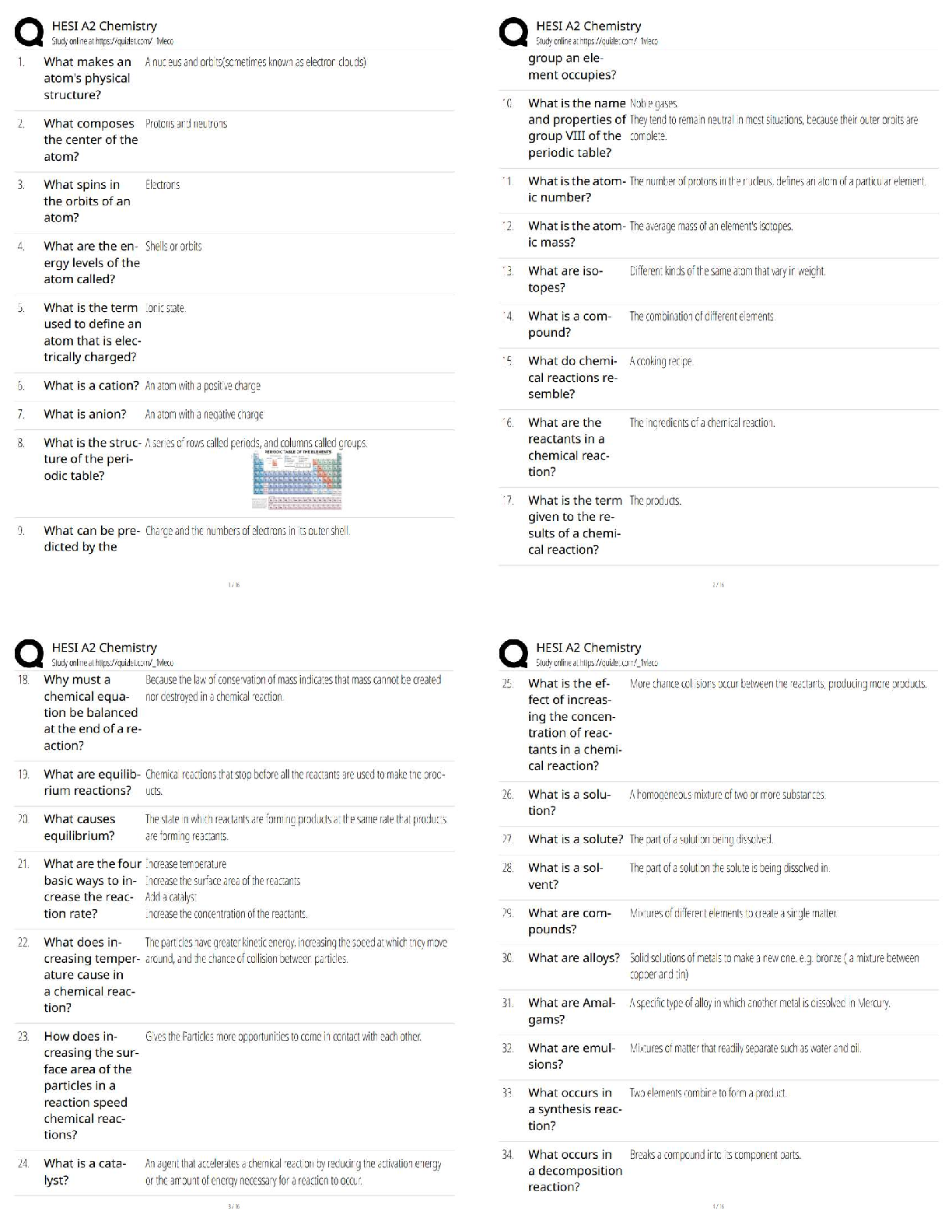
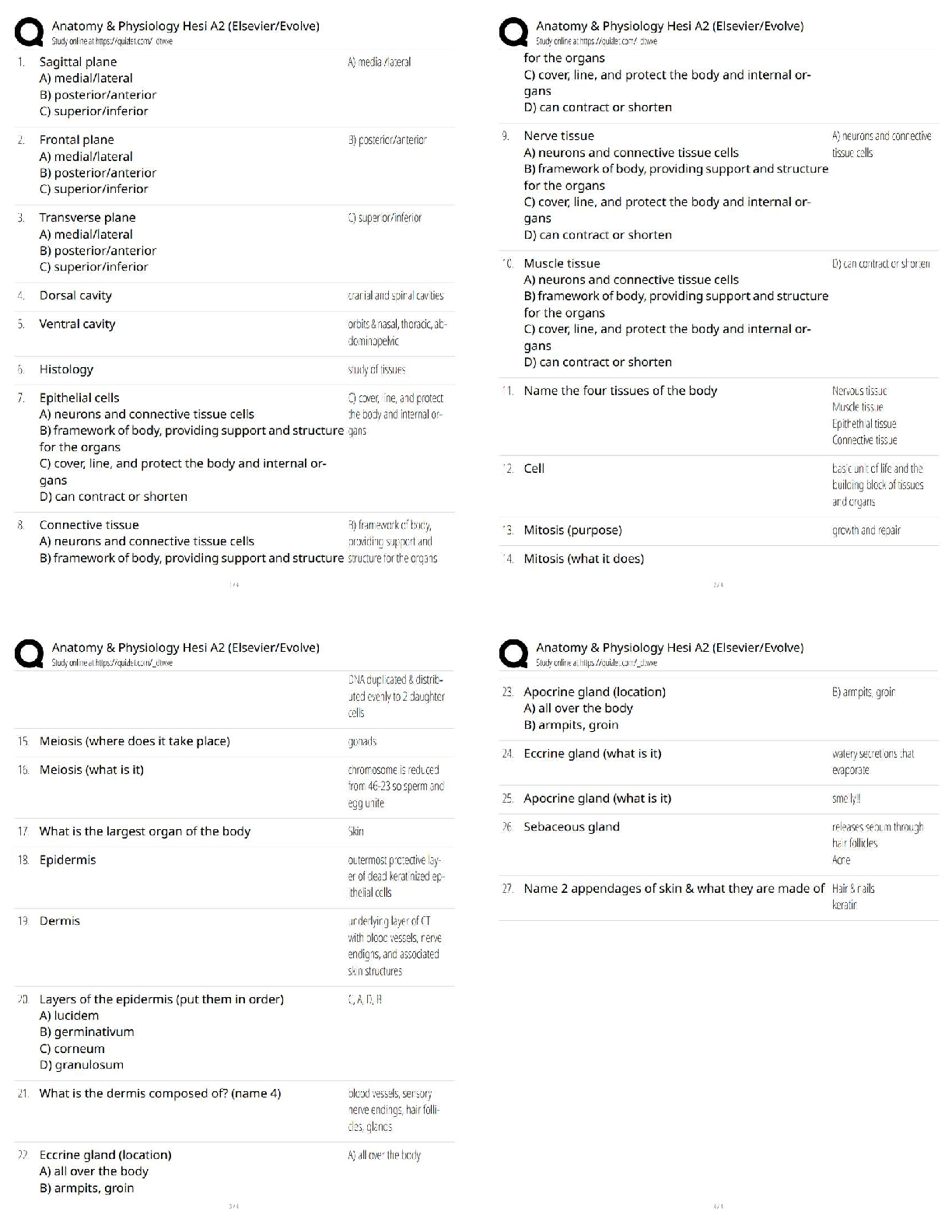
1. F( ) = 03i − 04j
All vectors in this field are identical, with length 05 and
parallel to h3 −4i.
2. F( ) = 1 2i + j
The length of the vector 1 2i + j is 1 42 + 2.
Vectors p
...
16.1 Vector Fields
1. F( ) = 03i − 04j
All vectors in this field are identical, with length 05 and
parallel to h3 −4i.
2. F( ) = 1 2i + j
The length of the vector 1 2i + j is 1 42 + 2.
Vectors point roughly away from the origin and vectors
farther from the origin are longer.
3. F( ) = − 1 2 i + ( − )j
The length of the vector − 1 2 i + ( − )j is
1 4 + ( − )2. Vectors along the line = are
horizontal with length 1 2.
4. F( ) = i + ( + )j
The length of the vector i + ( + )j is
2 + ( + )2. Vectors along the -axis are vertical,
and vectors along the line = − are horizontal with
length ||.
5. F( ) = i2++j2
The length of the vector i2++j2 is 1.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. 633
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.634 ¤ CHAPTER 16 VECTOR CALCULUS
6. F( ) = i2−+j2
All the vectors F( ) are unit vectors tangent to circles
centered at the origin with radius 2 + 2.
7. F( ) = i
All vectors in this field are identical, with length 1 and
pointing in the direction of the positive -axis.
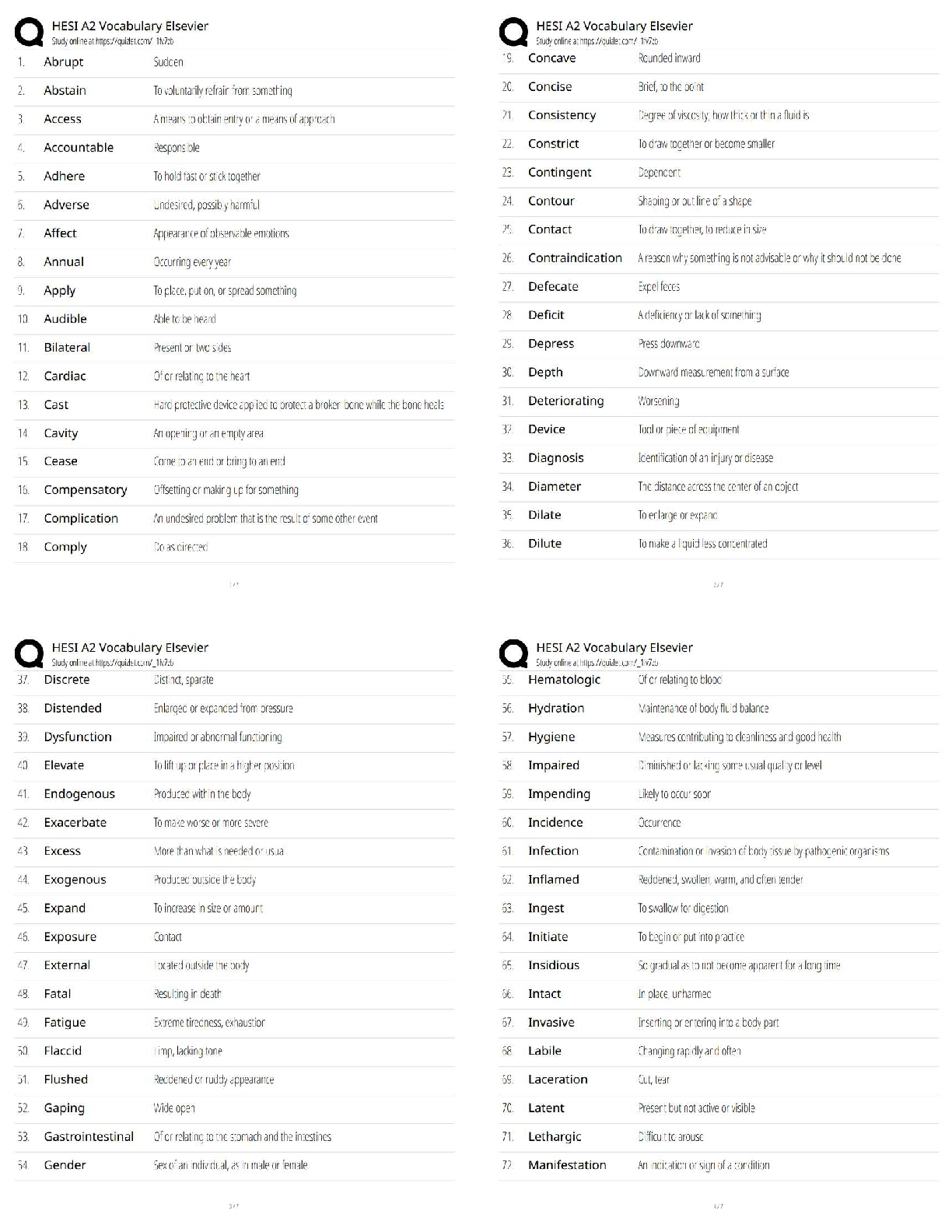
8. F( ) = i
At each point ( ), F( ) is a vector of length ||.
For 0, all point in the direction of the positive -axis,
while for 0, all are in the direction of the negative
-axis. In each plane = , all the vectors are identical.
9. F( ) = − i
At each point ( ), F( ) is a vector of length ||.
For 0, all point in the direction of the negative -axis,
while for 0, all are in the direction of the positive
-axis. In each plane = , all the vectors are identical.
10. F( ) = i + k
All vectors in this field have length √2 and point in the
same direction, parallel to the -plane.
11. F( ) = h −i corresponds to graph IV. In the first quadrant all the vectors have positive -components and negative
-components, in the second quadrant all vectors have negative - and -components, in the third quadrant all vectors have
negative -components and positive -components, and in the fourth quadrant all vectors have positive - and -components.
In addition, the vectors get shorter as we approach the origin.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.1 VECTOR FIELDS ¤ 635
12. F( ) = h − i corresponds to graph III. All vectors in quadrants I and II have positive -components while all vectors
in quadrants III and IV have negative -components. In addition, vectors along the line = are horizontal, and vectors get
shorter as we approach the origin.
13. F( ) = h + 2i corresponds to graph I. As in Exercise 12, all vectors in quadrants I and II have positive -components
while all vectors in quadrants III and IV have negative -components. Vectors along the line = −2 are horizontal, and the
vectors are independent of (vectors along horizontal lines are identical).
14. F( ) = hcos( + ) i corresponds to graph II. All vectors in quadrants I and IV have positive -components while all
vectors in quadrants II and III have negative -components. Also, the -components of vectors along any vertical line remain
constant while the -component oscillates.
15. F( ) = i + 2j + 3k corresponds to graph IV, since all vectors have identical length and direction.
16. F( ) = i + 2j + k corresponds to graph I, since the horizontal vector components remain constant, but the vectors
above the -plane point generally upward while the vectors below the -plane point generally downward.
17. F( ) = i + j + 3k corresponds to graph III; the projection of each vector onto the -plane is i + j, which points
away from the origin, and the vectors point generally upward because their -components are all 3.
18. F( ) = i + j + k corresponds to graph II; each vector F( ) has the same length and direction as the position
vector of the point ( ), and therefore the vectors all point directly away from the origin.
19. The vector field seems to have very short vectors near the line = 2.
For F( ) = h00i we must have 2 − 2 = 0 and 3 − 62 = 0.
The first equation holds if = 0 or = 2, and the second holds if
= 0 or = 2. So both equations hold [and thus F( ) = 0] along
the line = 2.
20. From the graph, it appears that all of the vectors in the field lie on lines
through the origin, and that the vectors have very small magnitudes near
the circle |x| = 2 and near the origin. Note that F(x) = 0 ⇔
( − 2) = 0 ⇔ = 0 or 2, so as we suspected, F(x) = 0 for
|x| = 2 and for |x| = 0. Note that where 2 − 0, the vectors point
towards the origin, and where 2 − 0, they point away from the
origin.
21. ( ) = sin() ⇒
∇( ) = ( )i + ( ) j = ( cos() · )i + [ · cos() + sin() · 1]j
= 2 cos()i + [ cos() + sin()]j
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.636 ¤ CHAPTER 16 VECTOR CALCULUS
22. ( ) = √2 + 3 ⇒
∇( ) = ( )i + ( )j = 1 2(2 + 3)−12 · 2i + 1 2(2 + 3)−12 · 3j = √21+ 3 i + 2√23+ 3 j
23. ( ) = 2 + 2 + 2 ⇒
∇( ) = ( )i + ( )j + ( )k
=
1 2
(2 + 2 + 2)−12(2)i + 1 2(2 + 2 + 2)−12(2)j + 1 2(2 + 2 + 2)−12(2)k
=
2 + 2 + 2 i + 2 +2 + 2 j + 2 +2 + 2 k
24. ( ) = 2 ⇒
∇( ) = ( )i + ( )j + ( )k
= 2 i + 2 · (1) + · 1j + 2(−2)k
= 2 i + 2 + 1j − 22 2 k
25. ( ) = 1 2( − )2 ⇒
∇( ) = ( − )(1)i + ( − )(−1)j = ( − )i + ( − )j.
The length of ∇( ) is ( − )2 + ( − )2 = √2 | − |.
The vectors are 0 along the line = . Elsewhere the vectors point
away from the line = with length that increases as the distance
from the line increases.
26. ( ) = 1 2(2 − 2) ⇒ ∇( ) = i − j.
The length of ∇( ) is 2 + 2. The lengths of the vectors
increase as the distance from the origin increases, and the terminal
point of each vector lies on the -axis.
27. We graph ∇( ) = 2
1 + 2 + 22 i + 1 + 42+ 22 j along with
a contour map of .
The graph shows that the gradient vectors are perpendicular to the
level curves. Also, the gradient vectors point in the direction in
which is increasing and are longer where the level curves are closer
together.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.1 VECTOR FIELDS ¤ 637
28. We graph ∇( ) = −sini − 2cos j along with a contour map
of .
The graph shows that the gradient vectors are perpendicular to the
level curves. Also, the gradient vectors point in the direction in
which is increasing and are longer where the level curves are closer
together.
29. ( ) = 2 + 2 ⇒ ∇( ) = 2i + 2j. Thus, each vector ∇( ) has the same direction and twice the length of
the position vector of the point ( ), so the vectors all point directly away from the origin and their lengths increase as we
move away from the origin. Hence, ∇ is graph III.
30. ( ) = ( + ) = 2 + ⇒ ∇( ) = (2 + )i + j. The -component of each vector is , so the vectors
point upward in quadrants I and IV and downward in quadrants II and III. Also, the -component of each vector is 0 along the
line = −2 so the vectors are vertical there. Thus, ∇ is graph IV.
31. ( ) = ( + )2 ⇒ ∇( ) = 2( + )i + 2( + )j. The - and -components of each vector are equal, so all
vectors are parallel to the line = . The vectors are 0 along the line = − and their length increases as the distance from
this line increases. Thus, ∇ is graph II.
32. ( ) = sin2 + 2 ⇒
∇( ) = cos2 + 2 · 1 2(2 + 2)−12(2)i + cos2 + 2 · 1 2(2 + 2)−12(2)j
=
cos2 + 2
2 + 2 i + cos 2+2 +22 j or cos 2+2 +22 (i + j)
Thus each vector is a scalar multiple of its position vector, so the vectors point toward or away from the origin with length that
changes in a periodic fashion as we move away from the origin. ∇ is graph I.
33. At = 3 the particle is at (21) so its velocity is V(21) = h43i. After 0.01 units of time, the particle’s change in
location should be approximately 001V(2 1) = 001h43i = h004003i, so the particle should be approximately at the
point (204 103).
34. At = 1 the particle is at (13) so its velocity is F(13) = h1 −1i. After 0.05 units of time, the particle’s change in
location should be approximately 005F(13) = 005h1 −1i = h005 −005i, so the particle should be approximately at
the point (105 295).
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.638 ¤ CHAPTER 16 VECTOR CALCULUS
35. (a) We sketch the vector field F( ) = i − j along with
several approximate flow lines. The flow lines appear to
be hyperbolas with shape similar to the graph of
= ±1, so we might guess that the flow lines have
equations = .
(b) If = () and = () are parametric equations of a flow line, then the velocity vector of the flow line at the
point ( ) is 0()i + 0 () j. Since the velocity vectors coincide with the vectors in the vector field, we have
0()i + 0()j = i − j ⇒ = , = −. To solve these differential equations, we know
= ⇒ = ⇒ ln|| = + ⇒ = ± + = for some constant , and
= − ⇒ = − ⇒ ln|| = − + ⇒ = ±− + = − for some constant . Therefore
= − = = constant. If the flow line passes through (11) then (1) (1) = constant = 1 ⇒ = 1 ⇒
= 1, 0.
36. (a) We sketch the vector field F( ) = i + j along with
several approximate flow lines. The flow lines appear to
be parabolas.
(b) If = () and = () are parametric equations of a flow line, then the velocity vector of the flow line at the
point ( ) is 0()i + 0()j. Since the velocity vectors coincide with the vectors in the vector field, we have
0()i + 0()j = i + j ⇒
= 1, = . Thus = = 1 = .
(c) From part (b), = . Integrating, we have = 1 22 + . Since the particle starts at the origin, we know (00) is on
the curve, so 0 = 0 + ⇒ = 0 and the path the particle follows is = 1 22.
16.2 Line Integrals
1. = 2 and = 2, 0 ≤ ≤ 3, so by Formula 3
= 03 2 2 + 2 = 03 2 (2)2 + (2)2 = 03 2 42 + 4
= 03 4 √2 + 1 = 2 · 2 3 2 + 1323 0 = 4 3(1032 − 1) or 4 3(10√10 − 1)
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.2 LINE INTEGRALS ¤ 639
2. = 3 and = 4, 1 ≤ ≤ 2, so by Formula 3
() = 12(34)(32)2 + (43)2 = 12(1) · 2√9 + 162 = 12 √9 + 162
=
1
32 ·
2 3
9 + 162322 1 = 48 1 (7332 − 2532) or 48 1 (73√73 − 125)
3. Parametric equations for are = 4 cos, = 4 sin, − 2 ≤ ≤ 2 . Then
4 = − 22(4 cos)(4 sin)4(−4sin)2 + (4 cos)2 = − 22 45 cos sin4 16(sin2 + cos2 )
= 45 − 22(sin4 cos)(4) = (4)6 1 5 sin5 − 2 2 = 46 · 2 5 = 16384
4. Parametric equations for are = 2 + 3, = 4, 0 ≤ ≤ 1. Then
= 01 (2 + 3)4 √32 + 42 = 501 (2 + 3)4
Integrating by parts with = 2 + 3 ⇒ = 3, = 4 ⇒ = 1 44 gives
= 5 1 4(2 + 3)4 − 16 3 41 0 = 5 5 44 − 16 3 4 − 1 2 + 16 3 = 85 164 − 25 16
5. If we choose as the parameter, parametric equations for are = , = 2 for 0 ≤ ≤ and by Equations 7
2 + sin = 0 2(2) + sin · 2 = 2 05 + sin
= 2 1 66 − cos + sin 0 where we integrated by parts in the second term
= 2 1 66 + + 0 − 0 = 1 36 + 2
6. Choosing as the parameter, we have = 3, = , −1 ≤ ≤ 1. Then
= −11 3 · 32 = 31 −1 = 1 − −1 = − 1.
7. = 1 + 2
On 1: = , = 1 2 ⇒ = 1 2 , 0 ≤ ≤ 2.
On 2: = , = 3 − ⇒ = −, 2 ≤ ≤ 3.
Then
( + 2) + 2 = 1( + 2) + 2 + 2( + 2) + 2
= 02 + 2 1 2 + 2 1 2 + 23 + 2(3 − ) + 2(−1)
= 02 2 + 1 22 + 23 6 − − 2
= 2 + 1 632 0 + 6 − 1 22 − 1 333 2 = 16 3 − 0 + 9 2 − 22 3 = 5 2
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.640 ¤ CHAPTER 16 VECTOR CALCULUS
8. = 1 + 2
On 1: = 2 cos ⇒ = −2sin , = 2 sin ⇒
= 2 cos , 0 ≤ ≤ 2 .
On 2: = 4 ⇒ = 4, = 2 + ⇒
= , 0 ≤ ≤ 1.
Then
2 + 2 = 1 2 + 2 + 2 2 + 2
= 02(2 cos)2(−2sin ) + (2 sin)2(2 cos ) + 01(4)2(4) + (2 + )2
= 8 02(−cos2 sin + sin2 cos) + 01(652 + 4 + 4)
= 8 1 3 cos3 + 1 3 sin3 0 2 + 65 3 3 + 22 + 41 0 = 8 1 3 − 1 3 + 65 3 + 2 + 4 = 83 3
9. = cos, = sin, = , 0 ≤ ≤ 2. Then by Formula 9,
2 = 02(cos )2(sin) 2 + 2 + 2
= 02 cos2 sin (−sin)2 + (cos )2 + (1)2 = 02 cos2 sin sin2 + cos2 + 1
= √2 02 cos2 sin = √2− 1 3 cos3 0 2 = √20 + 1 3 = √32
10. Parametric equations for are = 3 − 2, = 1 + , = 2 + 3, 0 ≤ ≤ 1. Then
2 = 01 (1 + )2(2 + 3)(−2)2 + 12 + 32 = √14 01 (33 + 82 + 7 + 2)
= √14 3 44 + 8 33 + 7 22 + 21 0 = √14 3 4 + 8 3 + 7 2 + 2 = 107 12 √14
11. Parametric equations for are = , = 2, = 3, 0 ≤ ≤ 1. Then
= 01 (2)(3)√12 + 22 + 32 = √14 01 62 = √14 12 1 621 0 = √12 14(6 − 1).
12. ()2 + ()2 + ()2 = 12 + (−2sin 2)2 + (2 cos 2)2 = 1 + 4(sin2 2 + cos2 2) = √5. Then
(2 + 2 + 2) = 02(2 + cos2 2 + sin2 2)√5 = √5 02(2 + 1)
= √5 1 33 + 2 0 = √5 1 3(83) + 2 = √5 8 33 + 2
13. = 01()(2)(2)(3) · 2 = 01 245 = 2 551 0 = 2 5(1 − 0) = 2 5( − 1)
14. + + = 14 · 1 2−12 + 2 · + √ · 2 = 14 1 212 + 2 + 232
= 1 332 + 1 33 + 4 5524 1 = 8 3 + 64 3 + 128 5 − 1 3 − 1 3 − 4 5 = 722 15
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.2 LINE INTEGRALS ¤ 641
15. Parametric equations for are = 1 + 3, = , = 2, 0 ≤ ≤ 1. Then
2 + 2 + 2 = 01(2)2 · 3 + (1 + 3)2 + 2 · 2 = 01 232 + 6 + 1
= 23 3 3 + 32 + 1 0 = 23 3 + 3 + 1 = 35 3
16. On 1: = ⇒ = = 0 ⇒
= 0 = ⇒ = 0 ≤ ≤ 1.
On 2: = 1 − ⇒ = − = ⇒
= = 1 + ⇒ = 0 ≤ ≤ 1.
Then
( + ) + ( + ) + ( + )
= 1 ( + ) + ( + ) + ( + ) + 2 ( + ) + ( + ) + ( + )
= 01(0 + ) + ( + ) · 0 + ( + 0) + 01( + 1 + )(−) + (1 − + 1 + ) + (1 − + )
= 01 2 + 01(−2 + 2) = 21 0 + −2 + 21 0 = 1 + 1 = 2
17. (a) Along the line = −3, the vectors of F have positive -components, so since the path goes upward, the integrand F · T is
always positive. Therefore 1 F · r = 1 F · T is positive.
(b) All of the (nonzero) field vectors along the circle with radius 3 are pointed in the clockwise direction, that is, opposite the
direction to the path. So F · T is negative, and therefore 2 F · r = 2 F · T is negative.
18. Vectors starting on 1 point in roughly the same direction as 1, so the tangential component F · T is positive. Then
1
F · r = 1 F · T is positive. On the other hand, no vectors starting on 2 point in the same direction as 2, while
some vectors point in roughly the opposite direction, so we would expect 2 F · r = 2 F · T to be negative.
19. r() = 3 i + 2 j, so F(r()) = (3)(2)2 i − (3)2 j = 7 i − 6 j and r0() = 32 i + 2j. Then
F · r = 01 F(r()) · r0() = 01(7 · 32 − 6 · 2) = 01(39 − 27) = 10 3 10 − 1 481 0 = 10 3 − 1 4 = 20 1 .
20. F(r()) = 2 + (3)2i + (2)(−2)j + (3 − 2)k = (2 + 6)i − 23 j + (3 − 2)k, r0() = 2i + 32 j − 2k. Then
F · r = 02 F(r()) · r0() = 02(23 + 27 − 65 − 23 + 4) = 02(27 − 65 + 4)
= 1 48 − 6 + 222 0 = 64 − 64 + 8 = 8
21. F · r = 01 sin3 cos(−2) 4 · 32 −2 1
= 01(32 sin3 − 2cos2 + 4) = −cos3 − sin2 + 1 551 0 = 6 5 − cos 1 − sin 1
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.642 ¤ CHAPTER 16 VECTOR CALCULUS
22. F · r = 0 hcos sincos sini · h−sin cos1i = 0 sin cos = 1 2 sin2 0 = 0
23. F(r()) = sin2 + sincos i + (sincos )sin2 j = sin2 + sincos i + cotj,
r0() = 2 sincosi + (cos2 − sin2 )j. Then
F · r = 63 F(r()) · r0() = 63 2sincossin2 + sincos + (cot)(cos2 − sin2 )
≈ 05424
24. F(r()) = (costan)sin i + (tansin)cos j + (sincos)tan k
= (sin)sin i + (tansin)cos j + (sin cos)tan k,
r0() = cosi − sinj + sec2 k. Then
F · r = 04 F(r()) · r0() = 04 (sincos)sin − (tansin2 )cos + (tan)tan ≈ 08527
25. = 2, = 3, = √ so by Formula 9,
arctan = 12(2)(3)arctan√ · (2)2 + (32)2 + 1(2√)2
= 12 542 + 94 + 1(4) arctan√ ≈ 948231
26. = 1 + 3, = 2 + 2, = 4 so by Formula 9,
ln( + ) = −11 4 ln(1 + 3 + 2 + 2) · (3)2 + (2)2 + (43)2
= −11 4√9 + 42 + 166 ln(3 + 3 + 2) ≈ 17260
27. We graph F( ) = ( − )i + j and the curve . We see that most of the vectors starting on point in roughly the same
direction as , so for these portions of the tangential component F · T is positive. Although some vectors in the third
quadrant which start on point in roughly the opposite direction, and hence give negative tangential components, it seems
reasonable that the effect of these portions of is outweighed by the positive tangential components. Thus, we would expect
F · r = F · T to be positive.
To verify, we evaluate F · r. The curve can be represented by r() = 2 cosi + 2 sinj, 0 ≤ ≤ 32 ,
so F(r()) = (2 cos − 2sin)i + 4 cossinj and r0() = −2sini + 2 cosj. Then
F · r = 032 F(r()) · r0()
= 032[−2sin(2 cos − 2sin) + 2 cos(4 cossin)]
= 4032(sin2 − sincos + 2 sincos2 )
= 3 + 2
3 [using a CAS]
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.2 LINE INTEGRALS ¤ 643
28. We graph F( ) = 2+ 2 i + 2+ 2 j and the curve . In the
first quadrant, each vector starting on points in roughly the same direction
as , so the tangential component F · T is positive. In the second quadrant,
each vector starting on points in roughly the direction opposite to , so
F · T is negative. Here, it appears that the tangential components in the first
and second quadrants counteract each other, so it seems reasonable to guess
that F · r = F · T is zero. To verify, we evaluate F · r. The curve can be represented by
r() = i + (1 + 2)j, −1 ≤ ≤ 1, so F(r()) = 2 + (1 + 2)2 i + 2 + (1 + 1 + 2 2)2 j and r0() = i + 2j. Then
F · r = −11 F(r()) · r0() = −11 2 + (1 + 2)2 + 22+ (1 + (1 + 2)2)2
= −11 √4(3 + 2 + 322+ 1 ) = 0 [since the integrand is an odd function]
29. (a) F · r = 01 2−1 5 · 2 32 = 01 22−1 + 37 = 2−1 + 3 881 0 = 11 8 − 1
(b) r(0) = 0, F(r(0)) = −10;
r √12 = 1 2 2√1 2, Fr √12 = −12 4√1 2;
r(1) = h11i, F(r(1)) = h11i.
In order to generate the graph with Maple, we use the line command in
the plottools package to define each of the vectors. For example,
v1:=line([0,0],[exp(-1),0]):
generates the vector from the vector field at the point (00) (but without an arrowhead) and gives it the name v1. To show
everything on the same screen, we use the display command. In Mathematica, we use ListPlot (with the
PlotJoined - True option) to generate the vectors, and then Show to show everything on the same screen.
30. (a) F · r = −11 2 23 · h2 3 −2i = −11(4 + 32 − 62) = 22 − 31 −1 = −2
(b) Now F(r()) = 2 2 3, so F(r(−1)) = h−2 1 −3i, Fr− 1 2 = −1 1 4 − 3 2, Fr 1 2 = 1 1 4 3 2,
and F(r(1)) = h2 13i.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.644 ¤ CHAPTER 16 VECTOR CALCULUS
31. = − cos 4, = − sin 4, = −, 0 ≤ ≤ 2 .
Then
= −(−sin 4)(4) − − cos 4 = −−(4 sin 4 + cos 4),
= −(cos 4)(4) − − sin 4 = −−(−4cos 4 + sin 4), and = −−, so
2 + 2 + 2 = (−−)2[(4sin4 + cos4)2 + (−4cos 4 + sin4)2 + 1]
= − 16(sin2 4 + cos2 4) + sin2 4 + cos2 4 + 1 = 3√2−
Therefore 32 = 02(− cos4)3(− sin4)2(−)(3√2−)
= 02 3√2−7 cos3 4sin2 4 = 5172 ,632,704 ,705√2(1 − −14)
32. (a) We parametrize the circle as r() = 2cosi + 2sinj, 0 ≤ ≤ 2. So F(r()) = 4cos2 4cossin,
r0() = h−2sin2cosi, and = F · r = 02(−8cos2 sin + 8 cos2 sin) = 0.
(b) From the graph, we see that all of the vectors in the field are
perpendicular to the path. This indicates that the field does no work
on the particle, since the field never pulls the particle in the direction
in which it is going. In other words, at any point along , F · T = 0,
and so certainly F · r = 0 .
33. We use the parametrization = 2 cos, = 2 sin, − 2 ≤ ≤ 2 . Then
= 2 + 2 = (−2sin)2 + (2 cos)2 = 2, so = = 2 − 22 = 2(),
= 1
2 = 21 − 22(2 cos )2 = 21 4sin − 2 2 = 4 , = 2 1 = 21 − 22(2 sin)2 = 0.
Hence ( ) = 4 0.
34. We use the parametrization = cos, = sin, 0 ≤ ≤ 2 . Then
= 2 + 2 = (−sin)2 + (cos)2 = , so
= ( ) = = 02 (cos)(sin) = 3 02 cos sin = 3 1 2 sin2 0 2 = 1 23,
=
1
32 () = 23 02 (cos)2(sin) = 23 · 4 02 cos2 sin
= 2− 1 3 cos3 0 2 = 2 0 + 1 3 = 2 3, and
=
1
32
() = 2
3 02 (cos)(sin)2 = 23 · 4 02 sin2 cos
= 2 1 3 sin3 0 2 = 2 1 3 − 0 = 2 3.
Therefore the mass is 1
23 and the center of mass is ( ) = 2 3 2 3.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.2 LINE INTEGRALS ¤ 645
35. (a) = 1
( ) , = 1 ( ), = 1 ( ) where = ( ).
(b) = = 02 4sin2 + 4cos2 + 9 = √1302 = 2 √13,
=
1
2 √13 02 2 √13 sin = 0, = 21√13 02 2 √13 cos = 0,
=
1
2 √13 02 √13(3) = 23 22 = 3. Hence ( ) = (003).
36. = (2 + 2 + 2) = 02(2 + 1) (1)2 + (−sin)2 + (cos)2 = 02(2 + 1)√2 = √2 8 33 + 2,
=
1
√2 8 33 + 2 02 √2(3 + ) = 48 343+ 2 + 22 = 3422 2+ 3 + 1,
=
3
2√2(42 + 3) 02 √2cos(2 + 1) = 0, and
=
3
2√2(42 + 3) 02 √2sin(2 + 1) = 0. Hence ( ) = 34(2 2 2+ 3 + 1)00.
37. From Example 3, ( ) = (1 − ), = cos, = sin, and = , 0 ≤ ≤ ⇒
= 2( ) = 0 sin2 [(1 − sin)] = 0(sin2 − sin3 )
=
1 2
0(1 − cos 2) − 0(1 − cos2 )sin Let in the second integral = cos , = − sin
= 2 + 1−1(1 − 2) = 2 − 4 3
= 2( ) = 0 cos2 (1 − sin) = 2 0(1 + cos 2) − 0 cos2 sin
= 2 − 2 3 , using the same substitution as above.
38. The wire is given as = 2 sin, = 2 cos, = 3, 0 ≤ ≤ 2 with ( ) = . Then
= (2 cos)2 + (−2sin)2 + 32 = 4(cos2 + sin2 ) + 9 = √13 and
= (2 + 2)( ) = 02(4 cos2 + 92)()√13 = √134 1 2 + 1 4 sin 2 + 332 0
= √13(4 + 243) = 4√13(1 + 62)
= (2 + 2)( ) = 02 4sin2 + 92()√13 = √134 1 2 − 1 4 sin 2 + 332 0
= √13(4 + 243) = 4√13(1 + 62)
= (2 + 2)( ) = 02(4 sin2 + 4 cos2 )()√13 = 4√13 02 = 8 √13
39. = F · r = 02 h − sin3 − cosi · h1 − cossini
= 02( − cos − sin + sincos + 3 sin − sincos )
= 02( − cos + 2 sin) = 1 22 − (sin + cos) − 2cos 2 0 in the second term integrate by parts
= 22
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.646 ¤ CHAPTER 16 VECTOR CALCULUS
40. Choosing as the parameter, the curve is parametrized by = 2 + 1, = , 0 ≤ ≤ 1. Then
= F · r = 01 2 + 12 2+1 · h21i = 01 2 2 + 12 + 2+1
= 1 3 2 + 13 + 1 2 2+11 0 = 8 3 + 1 2 2 − 1 3 − 1 2 = 1 2 2 − 1 2 + 7 3
41. r() = h2 1 − i, 0 ≤ ≤ 1.
= F · r =01 2 − 2 − (1 − )21 − − (2)2 · h21 −1i
= 01 (4 − 22 + − 1 + 2 − 2 − 1 + + 42) = 01 (2 + 8 − 2) = 1 3 3 + 42 − 21 0 = 7 3
42. r() = 2i + j + 5k, 0 ≤ ≤ 1. Therefore
= F · r = 01 (4 + 26 h2 25)3i2 · h015i = 01 (4 + 26 262)32 = −(4 + 262)−121 0 = 1 2 − √130 .
43. (a) r() = 2 i + 3 j ⇒ v() = r0() = 2i + 32 j ⇒ a() = v0() = 2i + 6j, and force is mass times
acceleration: F() = a() = 2i + 6j.
(b) = F · r =01(2i + 6j) · (2i + 32 j) = 01 (42 + 1823)
= 222 + 9 2 241 0 = 22 + 9 22
44. r() = sini+cosj+k ⇒ v() = r0() = cosi−sinj+k ⇒ a() = v0() = −sini−cosj
and F() = a() = −sini − cosj. Thus
= F · r =02(−sini − cosj) · (cosi − sinj + k)
= 02 (−2 sincos + 2 sincos) = (2 − 2) 1 2 sin2 0 2 = 1 2 (2 − 2)
45. The combined weight of the man and the paint is 185 lb, so the force exerted (equal and opposite to that exerted by gravity) is
F = 185k. To parametrize the staircase, let = 20 cos, = 20 sin, = 690 = 15 , 0 ≤ ≤ 6. Then the work done
is
= F · r = 06 h00 185i · −20 sin 20 cos 15 = (185) 15 06 = (185) 15 (6) ≈ 167 × 104 ft-lb
46. This time is a function of : = 185 − 9
6 = 185 − 23 . So let F = 185 − 23 k. To parametrize the staircase,
let = 20 cos, = 20 sin, = 690 = 15 , 0 ≤ ≤ 6. Therefore
= F · r = 06 00185 − 23 · −20 sin20 cos 15 = 15 06 185 − 23
=
15
185 − 43 26 0 = 90185 − 9 2 ≈ 162 × 104 ft-lb
47. (a) r() = hcos sini, 0 ≤ ≤ 2, and let F =h i. Then
= F · r =02 h i · h−sin cosi = 02(−sin + cos) = cos + sin2 0
= + 0 − + 0 = 0
(b) Yes. F( ) = x = h i and
= F · r =02 h cos sini · h−sincosi = 02(− sin cos + sin cos) = 02 0 = 0.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.2 LINE INTEGRALS ¤ 647
48. Consider the base of the fence in the -plane, centered at the origin, with the height given by = ( ). To graph the
fence, observe that the fence is highest when = 0 (where the height is 5 m) and lowest when = 0 (a height of 3 m). When
= ±, the height is 4 m.
Also, the fence can be graphed using parametric equations (see Section 16.6): = 10 cos , = 10 sin,
= 4 + 001((10 cos)2 − (10 sin)2) = (4 + cos2 − sin2 )
= (4 + cos 2), 0 ≤ ≤ 2, 0 ≤ ≤ 1.
The area of the fence is ( ) where , the base of the fence, is given by = 10 cos, = 10 sin, 0 ≤ ≤ 2.
Then
( ) = 02 4 + 001((10 cos)2 − (10 sin)2) (−10 sin)2 + (10 cos )2
= 02 (4 + cos 2)√100 = 104 + 1 2 sin 22 0 = 10(8) = 80 m2
If we paint both sides of the fence, the total surface area to cover is 160 m2, and since 1 L of paint covers 100 m2, we require
160
100 = 16 ≈ 503 L of paint.
49. Let r() = h() () ()i and v = h1 2 3i. Then
v · r = h1 2 3i · h0() 0() 0()i = [1 0() + 2 0() + 3 0()]
= 1 () + 2 () + 3 () = [1 () + 2 () + 3 ()] − [1 () + 2 () + 3 ()]
= 1 [() − ()] + 2 [() − ()] + 3 [() − ()]
= h1 2 3i · h() − () () − () () − ()i
= h1 2 3i · [h() () ()i − h() () ()i] = v · [r() − r()]
50. If r() = h() () ()i then
r · r = h() () ()i · h0() 0() 0()i = [()0() + ()0() + ()0()]
= 1 2[()]2 + 1 2[()]2 + 1 2[()]2
=
1 2
[()]2 + [()]2 + [()]2 − [()]2 + [()]2 + [()]2
=
1 2
|r()|2 − |r()|2
51. The work done in moving the object is F · r = F · T. We can approximate this integral by dividing into
7 segments of equal length ∆ = 2 and approximating F · T, that is, the tangential component of force, at a point (∗ ∗) on
each segment. Since is composed of straight line segments, F · T is the scalar projection of each force vector onto .
If we choose (∗ ∗) to be the point on the segment closest to the origin, then the work done is
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.648 ¤ CHAPTER 16 VECTOR CALCULUS
F· T ≈
7
= 1
[F(∗ ∗) · T(∗ ∗)] ∆ = [2 + 2 + 2 + 2 + 1 + 1 + 1](2) = 22. Thus, we estimate the work done to
be approximately 22 J.
52. Use the orientation pictured in the figure. Then since B is tangent to any circle that lies in the plane perpendicular to the wire,
B = |B|T where T is the unit tangent to the circle : = cos, = sin. Thus B = |B| h−sin cosi. Then
B · r = 02 |B| h−sincosi · h− sin cosi = 02 |B| = 2 |B|. (Note that |B| here is the magnitude
of the field at a distance from the wire’s center.) But by Ampere’s Law B · r = 0. Hence |B| = 0(2).
16.3 The Fundamental Theorem for Line Integrals
1. appears to be a smooth curve, and since ∇ is continuous, we know is differentiable. Then Theorem 2 says that the value
of ∇ · r is simply the difference of the values of at the terminal and initial points of . From the graph, this is
50 − 10 = 40.
2. is represented by the vector function r() = (2 + 1)i + (3 + )j, 0 ≤ ≤ 1, so r0() = 2i + (32 + 1)j. Since
32 + 1 6= 0, we have r0() 6= 0, thus is a smooth curve. ∇ is continuous, and hence is differentiable, so by Theorem 2
we have ∇ · r = (r(1)) − (r(0)) = (22) − (10) = 9 − 3 = 6.
3. Let ( ) = + 2 and ( ) = 2 + 2. Then = + 2 and = 2 + 2. Since 6= ,
F( ) = i + j is not conservative by Theorem 5.
4. (2 − 2) = 2 = (2) and the domain of F is R2 which is open and simply-connected, so F is conservative by
Theorem 6. Thus, there exists a function such that ∇ = F, that is, ( ) = 2 − 2 and ( ) = 2. But
( ) = 2 − 2 implies ( ) = 2 − 2 + () and differentiating both sides of this equation with respect to gives
( ) = 2 + 0(). Thus 2 = 2 + 0() so 0() = 0 and () = where is a constant. Hence
( ) = 2 − 2 + is a potential function for F.
5.
2 = 2 · + 2 = (2 + 2),
[(1 + )] = (1 + ) · + = + 2 + = (2 + 2).
Since these partial derivatives are equal and the domain of F is R2 which is open and simply-connected, F is conservative by
Theorem 6. Thus, there exists a function such that ∇ = F, that is, ( ) = 2 and ( ) = (1 + ). But
( ) = 2 implies ( ) = + () and differentiating both sides of this equation with respect to gives
( ) = (1 + ) + 0(). Thus (1 + ) = (1 + ) + 0() so 0() = 0 and () = where is a
constant. Hence ( ) = + is a potential function for F.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.3 THE FUNDAMENTAL THEOREM FOR LINE INTEGRALS ¤ 649
6. () = = ( + ) and the domain of F is R2 which is open and simply-connected, so F is conservative.
Hence there exists a function such that ∇ = F. Here ( ) = implies ( ) = + () and then
( ) = + 0(). But ( ) = + so 0() = ⇒ () = + and ( ) = + + is a
potential function for F.
7. ( + sin) = + cos = ( + cos) and the domain of F is R2. Hence F is conservative so there
exists a function such that ∇ = F. Then ( ) = + sin implies ( ) = + sin + () and
( ) = + cos + 0(). But ( ) = + cos so () = and ( ) = + sin + is a potential
function for F.
8. (2 + −2) = 2 − 2−3 = (2 − 2−3) and the domain of F is {( ) | 0} which is open and
simply-connected. Hence F is conservative, so there exists a function such that ∇ = F. Then ( ) = 2 + −2
implies ( ) = 2 + −2 + () and ( ) = 2 − 2−3 + 0(). But ( ) = 2 − 2−3 so
0() = 0 ⇒ () = . Then ( ) = 2 + −2 + is a potential function for F.
9. (2 cos + cos ) = 2 cos − sin = (2 sin − sin) and the domain of F is R2 which is open and simply
connected. Hence F is conservative so there exists a function such that ∇ = F. Then ( ) = 2 cos + cos implies
( ) = 2 sin + cos + () and ( ) = 2 sin − sin + 0(). But ( ) = 2 sin − sin so
0() = 0 ⇒ () = and ( ) = 2 sin + cos + is a potential function for F.
10. (ln + ) = 1 + 1 = (ln + ) and the domain of F is {( ) | 0 0} which is open and
simply connected. Hence F is conservative so there exists a function such that ∇ = F. Then ( ) = ln +
implies ( ) = ln + ln + () and ( ) = + ln + 0(). But ( ) = ln + so 0() = 0 ⇒
() = and ( ) = ln + ln + is a potential function for F.
11. (a) F has continuous first-order partial derivatives and
(2) = 2 = (2) on R2, which is open and
simply-connected. Thus, F is conservative by Theorem 6. Then we know that the line integral of F is independent of path;
in particular, the value of F · r depends only on the endpoints of . Since all three curves have the same initial and
terminal points, F · r will have the same value for each curve.
(b) We first find a potential function , so that ∇ = F. We know ( ) = 2 and ( ) = 2. Integrating
( ) with respect to , we have ( ) = 2 + (). Differentiating both sides with respect to gives
( ) = 2 + 0(), so we must have 2 + 0() = 2 ⇒ 0() = 0 ⇒ () = , a constant.
Thus ( ) = 2 + , and we can take = 0. All three curves start at (12) and end at (3 2), so by Theorem 2,
F · r = (3 2) − (12) = 18 − 2 = 16 for each curve.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.650 ¤ CHAPTER 16 VECTOR CALCULUS
12. (a) If F = ∇ then ( ) = 3 + 22 and ( ) = 22.
( ) = 3 + 22 implies ( ) = 3 + 22 + () and ( ) = 22 + 0(). But ( ) = 22 so
0() = 0 ⇒ () = . We can take = 0, so ( ) = 3 + 22.
(b) is a smooth curve with initial point (1 1) and terminal point 4 1 4 , so by Theorem 2
F · r = ∇ · r = 4 1 4 − (11) = (12 + 1) − (3 + 1) = 9.
13. (a) If F = ∇ then ( ) = 23 and ( ) = 32.
( ) = 23 implies ( ) = 1 3 33 + () and ( ) = 32 + 0(). But ( ) = 32 so 0() = 0 ⇒
() = , a constant. We can take = 0, so ( ) = 1 3 33.
(b) is a smooth curve with initial point r(0) = (0 0) and terminal point r(1) = (−13), so by Theorem 2
F · r = ∇ · r = (−13) − (00) = −9 − 0 = −9.
14. (a) ( ) = 2 implies ( ) = + () ⇒ ( ) = + + 0() = (1 + ) + 0(). But
( ) = (1 + ) so 0() = 0 ⇒ () = . We can take = 0, so ( ) = .
(b) The initial point of is r(0) = (10) and the terminal point is r(2) = (02), so
F · r = (02) − (10) = 0 − 0 = −1.
15. (a) ( ) = implies ( ) = + ( ) and so ( ) = + ( ). But ( ) = so
( ) = 0 ⇒ ( ) = (). Thus ( ) = + () and ( ) = + 0(). But
( ) = + 2, so 0() = 2 ⇒ () = 2 + . Hence ( ) = + 2 (taking = 0).
(b) F · r = (463) − (10 −2) = 81 − 4 = 77.
16. (a) ( ) = 2 + 22 implies ( ) = 2 + 22 + ( ) and so ( ) = 2 + ( ). But
( ) = 2 so ( ) = 0 ⇒ ( ) = (). Thus ( ) = 2 + 22 + () and
( ) = 2 + 22 + 0(). But ( ) = 2 + 22, so 0() = 0 ⇒ () = . Hence
( ) = 2 + 22 (taking = 0).
(b) = 0 corresponds to the point (0 1 0) and = 1 corresponds to (1 2 1), so
F · r = (121) − (010) = 5 − 0 = 5.
17. (a) ( ) = implies ( ) = + ( ) and so ( ) = + ( ). But ( ) = so
( ) = 0 ⇒ ( ) = (). Thus ( ) = + () and ( ) = + 0(). But
( ) = , so 0() = 0 ⇒ () = . Hence ( ) = (taking = 0).
(b) r(0) = h1 −1 0i, r(2) = h5 3 0i so F · r = (5 3 0) − (1 −10) = 30 + 0 = 4.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.3 THE FUNDAMENTAL THEOREM FOR LINE INTEGRALS ¤ 651
18. (a) ( ) = sin implies ( ) = sin + ( ) and so ( ) = cos + ( ). But
( ) = cos + cos so ( ) = cos ⇒ ( ) = cos + (). Thus
( ) = sin + cos + () and ( ) = − sin + 0(). But ( ) = − sin, so 0() = 0 ⇒
() = . Hence ( ) = sin + cos (taking = 0).
(b) r(0) = h000i, r(2) = h1 2 i so F · r = (1 2 ) − (000) = 1 − 2 − 0 = 1 − 2 .
19. The functions 2− and 2 − 2− have continuous first-order derivatives on R2 and
2− = −2− = 2 − 2−, so F( ) = 2− i + 2 − 2−j is a conservative vector field by
Theorem 6 and hence the line integral is independent of path. Thus a potential function exists, and ( ) = 2−
implies ( ) = 2− + () and ( ) = −2− + 0(). But ( ) = 2 − 2− so
0() = 2 ⇒ () = 2 + . We can take = 0, so ( ) = 2− + 2. Then
2− + (2 − 2−) = (21) − (10) = 4−1 + 1 − 1 = 4.
20. The functions sin and cos − sin have continuous first-order derivatives on R2 and
(sin) = cos = (cos − sin), so F( ) = sini + (cos − sin)j is a conservative vector field by
Theorem 6 and hence the line integral is independent of path. Thus a potential function exists, and ( ) = sin implies
( ) = sin + () and ( ) = cos + 0(). But ( ) = cos − sin so
0() = −sin ⇒ () = cos + . We can take = 0, so ( ) = sin + cos. Then
sin + (cos − sin) = (1 ) − (20) = −1 − 1 = −2.
21. If F is conservative, then F · r is independent of path. This means that the work done along all piecewise-smooth curves
that have the described initial and terminal points is the same. Your reply: It doesn’t matter which curve is chosen.
22. The curves 1 and 2 connect the same two points but 1 F · r 6=2 F · r. Thus F is not independent of path, and
therefore is not conservative.
23. F( ) = 3 i + 3 j, = F · r. Since (3) = 0 = (3), there exists a function such that ∇ = F. In
fact, ( ) = 3 ⇒ ( ) = 1 4 4 + () ⇒ ( ) = 0 + 0(). But ( ) = 3 so
0() = 3 ⇒ () = 1 4 4 + . We can take = 0 ⇒ ( ) = 1 4 4 + 1 4 4. Thus
= F · r = (22) − (10) = (4 + 4) − 1 4 + 0 = 31 4 .
24. F( ) = (2 + )i + j, = F · r. Since (2 + ) = 1 = (), there exists a function such that
∇ = F. In fact, ( ) = 2 + ⇒ ( ) = 2 + + () ⇒ ( ) = + 0(). But ( ) =
so 0() = 0 ⇒ () = . We can take = 0 ⇒ ( ) = 2 + . Thus
= F · r = (43) − (11) = (16 + 12) − (1 + 1) = 26.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.652 ¤ CHAPTER 16 VECTOR CALCULUS
25. We know that if the vector field (call it F) is conservative, then around any closed path , F · r = 0. But take to be a
circle centered at the origin, oriented counterclockwise. All of the field vectors that start on are roughly in the direction of
motion along , so the integral around will be positive. Therefore the field is not conservative.
26. If a vector field F is conservative, then around any closed path , F · r = 0. For any closed path we draw in the field, it
appears that some vectors on the curve point in approximately the same direction as the curve and a similar number point in
roughly the opposite direction. (Some appear perpendicular to the curve as well.) Therefore it is plausible that F · r = 0
for every closed curve which means F is conservative.
27. From the graph, it appears that F is conservative, since around all closed
paths, the number and size of the field vectors pointing in directions similar
to that of the path seem to be roughly the same as the number and size of the
vectors pointing in the opposite direction. To check, we calculate
(sin) = cos = (1 + cos). Thus F is conservative, by
Theorem 6.
28. ∇( ) = cos( − 2)i − 2cos( − 2)j
(a) We use Theorem 2: 1 F · r = 1 ∇ · r = (r()) − (r()) where 1 starts at = and ends at = . So
because (0 0) = sin0 = 0 and ( ) = sin( − 2) = 0, one possible curve 1 is the straight line from (00) to
( ); that is, r() = i + j, 0 ≤ ≤ 1.
(b) From (a), 2 F · r = (r()) − (r()). So because (0 0) = sin0 = 0 and 2 0 = 1, one possible curve 2 is
r() = 2 i, 0 ≤ ≤ 1, the straight line from (00) to 2 0.
29. Since F is conservative, there exists a function such that F = ∇, that is, = , = , and = . Since ,
, and have continuous first order partial derivatives, Clairaut’s Theorem says that = = = ,
= = = , and = = = .
30. Here F( ) = i + j + k. Then using the notation of Exercise 29, = 0 while = . Since these
aren’t equal, F is not conservative. Thus by Theorem 4, the line integral of F is not independent of path.
31. = {( ) | 0 3} consists of those points between, but not
on, the horizontal lines = 0 and = 3.
(a) Since does not include any of its boundary points, it is open. More
formally, at any point in there is a disk centered at that point that
lies entirely in .
(b) Any two points chosen in can always be joined by a path that lies
entirely in , so is connected. ( consists of just one “piece.”)
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.3 THE FUNDAMENTAL THEOREM FOR LINE INTEGRALS ¤ 653
(c) is connected and it has no holes, so it’s simply-connected. (Every simple closed curve in encloses only points that are
in .)
32. = {( ) | 1 || 2} consists of those points between, but
not on, the vertical lines = 1 and = 2, together with the points
between the vertical lines = −1 and = −2.
(a) The region does not include any of its boundary points, so it is open.
(b) consists of two separate pieces, so it is not connected. [For
instance, both the points (−150) and (150) lie in but they
cannot be joined by a path that lies entirely in .]
(c) Because is not connected, it’s not simply-connected.
33. = ( ) | 1 ≤ 2 + 2 ≤ 4 ≥ 0 is the semiannular region
in the upper half-plane between circles centered at the origin of radii
1 and 2 (including all boundary points).
(a) includes boundary points, so it is not open. [Note that at any
boundary point, (10) for instance, any disk centered there cannot lie
entirely in .]
(b) The region consists of one piece, so it’s connected.
(c) is connected and has no holes, so it’s simply-connected.
34. = {( ) | ( ) 6= (2 3)} consists of all points in the -plane
except for (2 3).
(a) has only one boundary point, namely (2 3), which is not included,
so the region is open.
(b) is connected, as it consists of only one piece.
(c) is not simply-connected, as it has a hole at (23). Thus any simple
closed curve that encloses (23) lies in but includes a point that is
not in .
35. (a) = −
2 + 2 ,
=
2 − 2
(2 + 2)2 and = 2 + 2 , = (22+−22)2 . Thus = .
(b) 1: = cos, = sin, 0 ≤ ≤ , 2: = cos, = sin, = 2 to = . Then
1 F · r = 0 (−sin)(cos −sin 2 + sin ) + (cos 2 )(cos) = 0 = and 2 F · r = 2 = −
Since these aren’t equal, the line integral of F isn’t independent of path. (Or notice that 3 F · r = 02 = 2 where
3 is the circle 2 + 2 = 1, and apply the contrapositive of Theorem 3.) This doesn’t contradict Theorem 6, since the
domain of F, which is R2 except the origin, isn’t simply-connected.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.654 ¤ CHAPTER 16 VECTOR CALCULUS
36. (a) Here F(r) = r|r|3 and r = i + j + k. Then (r) = −|r| is a potential function for F, that is, ∇ = F.
(See the discussion of gradient fields in Section 16.1.) Hence F is conservative and its line integral is independent of path.
Let 1 = (1 1 1) and 2 = (2 2 2).
= F · r = (2) − (1) = −
(2 2 + 22 + 22)12 +
(2 1 + 12 + 12)12 = 11 − 12 .
(b) In this case, = −() ⇒
= −152 ×1 1011 − 147 ×1 1011
= −(597 × 1024)(199 × 1030)(667 × 10−11)(−22377 × 10−13) ≈ 177 × 1032 J
(c) In this case, = ⇒
= 101−12 − 5 × 10 1 −13 = 8985 × 109(1)−16 × 10−19−1012 ≈ 1400 J.
16.4 Green's Theorem
1. (a) 1: = ⇒ = = 0 ⇒ = 0 0 ≤ ≤ 5.
2: = 5 ⇒ = 0 = ⇒ = 0 ≤ ≤ 4.
3: = 5 − ⇒ = − = 4 ⇒ = 0 0 ≤ ≤ 5.
4: = 0 ⇒ = 0 = 4 − ⇒ = − 0 ≤ ≤ 4
Thus 2 + 2 =
1 + 2 + 3 + 4
2 + 2 = 05 0 + 04 25 + 05(−16 + 0) + 04 0
= 0 + 25 2 24 0 + [−16]5 0 + 0 = 200 + (−80) = 120
(b) Note that as given in part (a) is a positively oriented, piecewise-smooth, simple closed curve. Then by Green’s Theorem,
2 + 2 = (2) − (2) = 05 04(2 − 2) = 05 2 − 2 =4 =0
= 05(16 − 16) = 82 − 165 0 = 200 − 80 = 120
2. (a) Parametric equations for are = 4 cos, = 4 sin, 0 ≤ ≤ 2. Then = −4sin , = 4 cos and
− = 02[(4 sin)(−4sin) − (4 cos)(4 cos)]
= −1602(sin2 + cos2 ) = −1602 1 = −16(2) = −32
(b) Note that as given in part (a) is a positively oriented, smooth, simple closed curve. Then by Green’s Theorem,
− = (−) − () = (−1 − 1) = −2
= −2(area of ) = −2 · (4)2 = −32
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.4 GREEN’S THEOREM ¤ 655
3. (a) 1: = ⇒ = , = 0 ⇒ = 0, 0 ≤ ≤ 1.
2: = 1 ⇒ = 0, = ⇒ = , 0 ≤ ≤ 2.
3: = 1 − ⇒ = −, = 2 − 2 ⇒ = −2, 0 ≤ ≤ 1.
Thus + 23 =
1 + 2 + 3
+ 23
= 01 0 + 02 3 + 01 −(1 − )(2 − 2) − 2(1 − )2(2 − 2)3
= 0 + 1 442 0 + 01 −2(1 − )2 − 16(1 − )5
= 4 + 2 3(1 − )3 + 8 3(1 − )61 0 = 4 + 0 − 10 3 = 2 3
(b) + 23 = (23) − () = 01 02(23 − )
= 01 1 24 − =2 =0 = 01(85 − 22) = 4 3 − 2 3 = 2 3
4. (a) 1: = ⇒ = , = 2 ⇒ = 2 , 0 ≤ ≤ 1
2: = 1 − ⇒ = −, = 1 ⇒ = 0, 0 ≤ ≤ 1
3: = 0 ⇒ = 0, = 1 − ⇒ = −, 0 ≤ ≤ 1
Thus
22 + =
1+2+3
22 +
= 01 2(2)2 + (2)(2 ) + 01 (1 − )2(1)2(−) + (1 − )(1)(0)
+01 (0)2(1 − )2(0) + (0)(1 − )(−)
= 01 6 + 24 + 01 −1 + 2 − 2 + 01 0
= 1 77 + 2 551 0 + − + 2 − 1 331 0 + 0 = 1 7 + 2 5 + −1 + 1 − 1 3 = 105 22
(b) 22 + = () − (22) = 01 12( − 22)
= 01 1 22 − 22 =1 =2 = 01 1 2 − 2 − 1 24 + 6
= 1 2 − 1 33 − 10 1 5 + 1 771 0 = 1 2 − 1 3 − 10 1 + 1 7 = 105 22
5. The region enclosed by is [03] × [04], so
+ 2 = (2) − () = 03 04 (2 − )
= 03 04 = 3 0 4 0 = (3 − 0)(4 − 0) = 4(3 − 1)
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.656 ¤ CHAPTER 16 VECTOR CALCULUS
6. The region enclosed by is given by {( ) | 0 ≤ ≤ 1 0 ≤ ≤ 2}, so
(2 + 2) + (2 − 2) = (2 − 2) − (2 + 2)
= 01 02(2 − 2)
= 01 2 − 2 =2 =0
= 01(42 − 42) = 01 0 = 0
7. + √ + (2 + cos 2) = (2 + cos 2) − + √
= 01√2(2 − 1) = 01(√ − 2) = 2 332 − 1 331 0 = 1 3
8. 4 + 23 = (23) − (4) = (23 − 43)
= −2 3 = 0
because ( ) = 3 is an odd function with respect to and is symmetric about the -axis.
9. 3 − 3 = (−3) − (3) = (−32 − 32) = 02 02(−32)
= −302 02 3 = −32 0 1 442 0 = −3(2)(4) = −24
10. (1 − 3) + (3 + 2) = (3 + 2) − (1 − 3) = (32 + 32)
= 02 23 (32) = 3 02 23 3
= 32 0 1 443 2 = 3(2) · 1 4(81 − 16) = 195 2
11. F( ) = h cos − sin + cos i and the region enclosed by is given by
{( ) | 0 ≤ ≤ 2 0 ≤ ≤ 4 − 2}. is traversed clockwise, so − gives the positive orientation.
F · r = − −( cos − sin) + ( + cos) = − ( + cos) − ( cos − sin)
= − ( − sin + cos − cos + sin) = − 02 04−2
= − 02 1 22 =4 =0−2 = − 02 12(4 − 2)2 = − 02(8 − 8 + 22) = − 8 − 42 + 2 332 0
= − 16 − 16 + 16 3 − 0 = − 16 3
12. F( ) = − + 2 − + 2 and the region enclosed by is given by {( ) | −2 ≤ ≤ 2 0 ≤ ≤ cos}.
is traversed clockwise, so − gives the positive orientation.
F · r = − − − + 2 + − + 2 = − − + 2 − − + 2
= − − 22 0cos (2 − 2) = − − 22 2 − 2 =cos =0
= − − 22(2cos − cos2 ) = − − 22 2cos − 1 2(1 + cos2)
= − 2sin + 2cos − 1 2 + 1 2 sin2 − 2 2 [integrate by parts in the first term]
= − − 1 4 − − 1 4 = 1 2
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.4 GREEN’S THEOREM ¤ 657
13. F( ) = h − cos sini and the region enclosed by is the disk with radius 2 centered at (3 −4).
is traversed clockwise, so − gives the positive orientation.
F · r = − −( − cos) + (sin) = − (sin) − ( − cos)
= − (sin − 1 − sin) = = area of = (2)2 = 4
14. F( ) = √2 + 1tan−1 and the region enclosed by is given by {( ) | 0 ≤ ≤ 1 ≤ ≤ 1}.
is oriented positively, so
F · r = √2 + 1 + tan−1 = tan−1 − (2 + 1)
= 01 1 1 +12 − 0 = 01 1 +12 =1 = = 01 1 +12 (1 − )
= 01 1 +12 − 1 +2 = tan−1 − 12 ln(1 + 2)1 0 = 4 − 12 ln2
15. Here = 1 + 2 where
1 can be parametrized as = , = 0, −2 ≤ ≤ 2, and
2 is given by = −, = cos, −2 ≤ ≤ 2.
Then the line integral is
1+2
34 + 54 = − 22(0 + 0) + − 22[(−)3(cos)4(−1) + (−)5(cos)4(−sin)]
= 0 + − 22(3 cos4 + 5 cos4 sin) = 15 1 4 − 4144 11252 + 7253 ,578,125 ,368 ≈ 00779
according to a CAS. The double integral is
− = − 220cos (544 − 433) = 15 1 4 − 4144 11252 + 7253 ,578,125 ,368 ≈ 00779, verifying Green’s
Theorem in this case.
16. We can parametrize as = cos, = 2 sin, 0 ≤ ≤ 2. Then the line integral is
+ = 02 2cos − (cos )3(2 sin)5(−sin) + 02(cos)3(2 sin)8 · 2cos
= 02(−2cos sin + 32 cos3 sin6 + 512 cos4 sin8 ) = 7,
according to a CAS. The double integral is − = −11 −√√44−−4422(328 + 534) = 7.
17. By Green’s Theorem, = F · r = ( + ) + 2 = (2 − ) where is the path described in the
question and is the triangle bounded by . So
= 0101−(2 − ) = 01 1 33 − = 1 = 0− = 01 1 3(1 − )3 − (1 − )
= − 12 1 (1 − )4 − 1 22 + 1 331 0 = − 1 2 + 1 3 − − 12 1 = − 12 1
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.658 ¤ CHAPTER 16 VECTOR CALCULUS
18. By Green’s Theorem, = F · r = sin + sin + 2 + 1 33 = (2 + 2 − 0), where
is the region (a quarter-disk) bounded by . Converting to polar coordinates, we have
= 0205 2 · = 0 2 1 445 0 = 1 2 625 4 = 625 8 .
19. Let 1 be the arch of the cycloid from (0 0) to (20), which corresponds to 0 ≤ ≤ 2, and let 2 be the segment from
(20) to (00), so 2 is given by = 2 − , = 0, 0 ≤ ≤ 2. Then = 1 ∪ 2 is traversed clockwise, so − is
oriented positively. Thus − encloses the area under one arch of the cycloid and from (5) we have
= − − = 1 + 2 = 02(1 − cos)(1 − cos) + 02 0(−)
= 02(1 − 2cos + cos2 ) + 0 = − 2sin + 1 2 + 1 4 sin 22 0 = 3
20. = = 02(5 cos − cos 5)(5 cos − 5cos 5)
= 02(25 cos2 − 30 cos cos 5 + 5 cos2 5)
= 25 1 2 + 1 4 sin 2 − 30 1 8 sin 4 + 12 1 sin 6 + 5 1 2 + 20 1 sin 102 0
[Use Formula 80 in the Table of Integrals]
= 30
21. (a) Using Equation 16.2.8, we write parametric equations of the line segment as = (1 − )1 + 2, = (1 − )1 + 2,
0 ≤ ≤ 1. Then = (2 − 1) and = (2 − 1), so
− = 01 [(1 − )1 + 2](2 − 1) + [(1 − )1 + 2](2 − 1)
= 01 (1(2 − 1) − 1(2 − 1) + [(2 − 1)(2 − 1) − (2 − 1)(2 − 1)])
= 01 (12 − 21) = 12 − 21
(b) We apply Green’s Theorem to the path = 1 ∪ 2 ∪ · · · ∪ , where is the line segment that joins ( ) to
(+1 +1) for = 1, 2, , − 1, and is the line segment that joins ( ) to (1 1). From (5),
1 2
− = , where is the polygon bounded by . Therefore
area of polygon = () = = 1 2 −
=
1 2
1 − + 2 − + · · · + −1 − + −
To evaluate these integrals we use the formula from (a) to get
() = 1 2[(12 − 21) + (23 − 32) + · · · + (−1 − −1) + (1 − 1)].
(c) = 1 2[(0 · 1 − 2 · 0) + (2 · 3 − 1 · 1) + (1 · 2 − 0 · 3) + (0 · 1 − (−1) · 2) + (−1 · 0 − 0 · 1)]
=
1 2
(0 + 5 + 2 + 2) = 9 2
22. By Green’s Theorem, 212 = 21 2 = 1 = and
−
1
22 = − 21 (−2) = 1 = .
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.4 GREEN’S THEOREM ¤ 659
23. We orient the quarter-circular region as shown in the figure.
= 1
42 so = 1
22 2 and = −122 2.
Here = 1 + 2 + 3 where 1: = , = 0, 0 ≤ ≤ ;
2: = cos, = sin, 0 ≤ ≤ 2 ; and
3: = 0, = − , 0 ≤ ≤ . Then
2 = 1 2 + 2 2 + 3 2 = 0 0 + 02(cos)2(cos ) + 0 0
= 02 3 cos3 = 3 02(1 − sin2 )cos = 3sin − 1 3 sin3 0 2 = 2 33
so =
1
222 = 34 .
2 = 1 2 + 2 2 + 3 2 = 0 0 + 02(sin)2(−sin) + 0 0
= 02(−3 sin3 ) = −3 02(1 − cos2 )sin = −3 1 3 cos3 − cos 0 2 = − 2 33,
so = −
1
222 = 34 . Thus ( ) = 34 34 .
24. Here = 1
2 and = 1 + 2 + 3, where 1: = , = 0, 0 ≤ ≤ ;
2: = , = , 0 ≤ ≤ ; and 3: = , = , = to = 0. Then
2 = 1 2 + 2 2 + 3 2 = 0 + 0 2 + 0(2)
= 2 +
1 330 = 2 − 1 32 = 2 32
Similarly, 2 = 1 2 + 2 2 + 3 2 = 0 + 0 + 0 2 = 22 · 1 330 = − 1 32. Thus
= 1
22 = 1 · 2 32 = 2 3 and = − 212 = − 1 − 1 32 = 1 3, so ( ) = 2 3 1 3.
25. By Green’s Theorem, − 1 33 = − 1 3 (−32) = 2 = and
1 3
3 = 1 3 (32) = 2 = .
26. By symmetry the moments of inertia about any two diameters are equal. Centering the disk at the origin, the moment of inertia
about a diameter equals
=
1 3
3 = 1 3 02(4 cos4 ) = 1 34 02 3 8 + 1 2 cos 2 + 1 8 cos 4 = 1 34 · 3(28) = 1 44
27. As in Example 5, let 0 be a counterclockwise-oriented circle with center the origin and radius , where is chosen to
be small enough so that 0 lies inside , and the region bounded by and 0. Here
= 2
(2 + 2)2 ⇒
=
2(2 + 2)2 − 2 · 2(2 + 2) · 2
(2 + 2)4 =
23 − 62
(2 + 2)3 and
= 2 − 2
(2 + 2)2 ⇒
=
−2(2 + 2)2 − (2 − 2) · 2(2 + 2) · 2
(2 + 2)4 =
23 − 62
(2 + 2)3 . Thus, as in the example,
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.660 ¤ CHAPTER 16 VECTOR CALCULUS
+ + −0 + = − = 0 = 0
and F · r = 0 F · r. We parametrize 0 as r() = cosi + sinj, 0 ≤ ≤ 2. Then
F · r = 0 F · r = 02 2(cos)(sin 2 cos ) 2i + +22sin sin22−2 2 cos2 j · − sini + cosj
=
1
02 −cossin2 − cos3 = 1 02 −cossin2 − cos 1 − sin2
= −
1
02 cos = −1 sin2 0 = 0
28. and have continuous partial derivatives on R2, so by Green’s Theorem we have
F · r = − = (3 − 1) = 2 = 2 · () = 2 · 6 = 12
29. Since is a simple closed path which doesn’t pass through or enclose the origin, there exists an open region that doesn’t
contain the origin but does contain . Thus = −(2 + 2) and = (2 + 2) have continuous partial derivatives on
this open region containing and we can apply Green’s Theorem. But by Exercise 16.3.35(a), = , so
F · r = 0 = 0.
30. We express as a type II region: = {( ) | 1() ≤ ≤ 2(), ≤ ≤ } where 1 and 2 are continuous functions.
Then = 1(2()) = [(2() ) − (1() )] by the Fundamental Theorem of
Calculus. But referring to the figure, =
1 + 2 + 3 + 4
.
Then 1 = (1() ), 2 = 4 = 0,
and 3 = (2() ). Hence
= [(2() ) − (1() )] = ().
31. Using the first part of (5), we have that = () = . But = ( ), and = + ,
and we orient by taking the positive direction to be that which corresponds, under the mapping, to the positive direction
along , so
= ( ) + = ( ) + ( )
= ± ( ) − ( ) [using Green’s Theorem in the -plane]
= ± + ( ) 2 − − ( ) 2 [using the Chain Rule]
= ± − [by the equality of mixed partials] = ± (( ))
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.5 CURL AND DIVERGENCE ¤ 661
The sign is chosen to be positive if the orientation that we gave to corresponds to the usual positive orientation, and it is
negative otherwise. In either case, since () is positive, the sign chosen must be the same as the sign of ( )
( ) .
Therefore () = = (( ) ) .
16.5 Curl and Divergence
1. (a) curlF = ∇ × F =
i j k
22 22 22
= (22) − (22)i − (22) − (22)j + (22) − (22)k
= (22 − 22)i − (22 − 22)j + (22 − 22)k = 0
(b) divF = ∇ · F =
(22) + (22) + (22) = 22 + 22 + 22
2. (a) curlF = ∇ × F =
i j k
0 32 43
= (43) − (32)i − (43) − (0)j + (32) − (0)k
= (433 − 23)i − (0 − 0)j + (322 − 0)k = (433 − 23)i + 322 k
(b) divF = ∇ · F =
(0) + (32) + (43) = 0 + 32 + 342 = 32 + 342
3. (a) curlF = ∇ × F =
i j k
0
= ( − 0)i − ( − )j + (0 − )k
= i + ( − )j − k
(b) divF = ∇ · F =
() + (0) + () = + 0 + = ( + )
4. (a) curlF = ∇ × F =
i j k
sin sin sin
= (cos − cos )i − ( cos − cos)j + ( cos − cos )k
= (cos − cos)i + (cos − cos)j + (cos − cos)k
(b) divF = ∇ · F =
(sin) + (sin) + (sin) = 0 + 0 + 0 = 0
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.662 ¤ CHAPTER 16 VECTOR CALCULUS
5. (a) curlF = ∇ × F =
i j k
√
1 +
√
1 +
√
1 +
= √ (−1)(1 + )−2 − 0i − 0 − √(−1)(1 + )−2j + √ (−1)(1 + )−2 − 0k
= −
√
(1 + )2 i −
√
(1 + )2 j −
√
(1 + )2 k
(b) divF = ∇ · F =
1 + √ + 1 + √ + 1 + √
=
1
2√(1 + ) +
1
2√ (1 + ) +
1
2√ (1 + )
6. (a) curlF = ∇ × F =
i j k
ln(2 + 3) ln( + 3) ln( + 2)
= + 2 2 − + 3 3 i − + 2 1 − 2 + 3 3 j + + 3 1 − 2 + 3 2 k
= + 2 2 − + 3 3 i + 2 + 3 3 − + 2 1 j + + 3 1 − 2 + 3 2 k
(b) divF = ∇ · F =
ln(2 + 3) + ln( + 3) + ln( + 2) = 0 + 0 + 0 = 0
7. (a) curlF = ∇ × F =
i j k
sin sin sin
= (0 − cos)i − ( cos − 0)j + (0 − cos)k
= h− cos − cos − cosi
(b) divF = ∇ · F =
( sin) + ( sin) + ( sin) = sin + sin + sin
8. (a) curlF = ∇ × F =
i j k
arctan() arctan() arctan()
= 0 − 1 + ()2 i − 1 + ()2 − 0j + 0 − 1 + ()2 k
= −1 +22 −1 +22 −1 +22
(b) divF = ∇ · F =
arctan() + arctan() + [arctan()] = 1 +22 + 1 +22 + 1 +22
9. If the vector field is F = i + j + k, then we know = 0. In addition, the -component of each vector of F is 0, so
= 0, hence
=
=
=
=
=
= 0. decreases as increases, so 0, but doesn’t change
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.5 CURL AND DIVERGENCE ¤ 663
in the - or -directions, so
=
= 0.
(a) divF =
+
+
= 0 + + 0 0
(b) curlF = − i + − j + − k = (0 − 0)i + (0 − 0)j + (0 − 0)k = 0
10. If the vector field is F = i + j + k, then we know = 0. In addition, and don’t vary in the -direction, so
=
=
=
=
= 0. As increases, the -component of each vector of F increases while the -component
remains constant, so
0 and = 0. Similarly, as increases, the -component of each vector increases while the
-component remains constant, so
0 and = 0.
(a) divF =
+
+
=
+
+ 0 0
(b) curlF = − i + − j + − k = (0 − 0)i + (0 − 0)j + (0 − 0)k = 0
11. If the vector field is F = i + j + k, then we know = 0. In addition, the -component of each vector of F is 0, so
= 0, hence
=
=
=
=
=
= 0. increases as increases, so 0, but doesn’t change in
the - or -directions, so
=
= 0.
(a) divF =
+
+
= 0 + 0 + 0 = 0
(b) curlF = − i + − j + − k = (0 − 0)i + (0 − 0)j + 0 − k = − k
Since
0, − k is a vector pointing in the negative -direction.
12. (a) curl = ∇ × is meaningless because is a scalar field.
(b) grad is a vector field.
(c) divF is a scalar field.
(d) curl (grad) is a vector field.
(e) gradF is meaningless because F is not a scalar field.
(f ) grad(divF) is a vector field.
(g) div(grad) is a scalar field.
(h) grad(div ) is meaningless because is a scalar field.
(i) curl(curlF) is a vector field.
(j) div(divF) is meaningless because div F is a scalar field.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.664 ¤ CHAPTER 16 VECTOR CALCULUS
(k) (grad) × (divF) is meaningless because divF is a scalar field.
(l) div(curl(grad)) is a scalar field.
13. curlF = ∇ × F =
i j k
23 23 322
= (62 − 62)i − (322 − 322)j + (23 − 23)k = 0
and F is defined on all of R3 with component functions which have continuous partial derivatives, so by Theorem 4,
F is conservative. Thus, there exists a function such that F = ∇. Then ( ) = 23 implies
( ) = 23 + ( ) and ( ) = 23 + ( ). But ( ) = 23, so ( ) = () and
( ) = 23 + (). Thus ( ) = 322 + 0() but ( ) = 322 so () = , a constant.
Hence a potential function for F is ( ) = 23 + .
14. curlF = ∇ × F =
i j k
4 24 423
= (423 − 423)i − (83 − 43)j + (24 − 4)k 6= 0,
so F is not conservative.
15. curlF = ∇ × F =
i j k
cos sin cos
= (−sin − sin)i − (cos − cos)j + [ sin − (− sin)]k = −2sin i + 2 sink 6= 0,
so F is not conservative.
16. curlF = ∇ × F =
i j k
1 sin cos
= (cos − cos)i − (0 − 0)j + (0 − 0)k = 0, F is defined on all of R3,
and the partial derivatives of the component functions are continuous, so F is conservative. Thus there exists a function
such that ∇ = F. Then ( ) = 1 implies ( ) = + ( ) and ( ) = ( ). But
( ) = sin, so ( ) = sin + () and ( ) = + sin + (). Thus ( ) = cos + 0() but
( ) = cos so () = and ( ) = + sin + .
17. curlF = ∇ × F =
i j k
= [ + − ( + )]i − ( − )j + ( − )k = 0
F is defined on all of R3, and the partial derivatives of the component functions are continuous, so F is conservative. Thus
there exists a function such that ∇ = F. Then ( ) = implies ( ) = + ( ) ⇒
( ) = + ( ). But ( ) = , so ( ) = () and ( ) = + ().
Thus ( ) = + 0() but ( ) = so () = and a potential function for F is
( ) = + .
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.5 CURL AND DIVERGENCE ¤ 665
18. curlF = ∇ × F =
i j k
sin cos cos
= [− sin + cos − (− sin + cos)]i − ( cos − cos)j
+( cos − cos)k = 0
F is defined on all of R3, and the partial derivatives of the component functions are continuous, so F is conservative. Thus
there exists a function such that ∇ = F. Then ( ) = sin implies ( ) = sin + ( ) ⇒
( ) = cos + ( ). But ( ) = cos, so ( ) = () and ( ) = sin + ().
Thus ( ) = cos + 0() but ( ) = cos so () = and a potential function for F is
( ) = sin + .
19. No. Assume there is such a G. Then div(curlG) =
(sin) + (cos) + ( − ) = sin − sin + 1 6= 0,
which contradicts Theorem 11.
20. No. Assume there is such a G. Then div(curlG) =
() + () + () = 1 + 1 + 1 6= 0 which contradicts
Theorem 11.
21. curlF =
i j k
() () ()
= (0 − 0)i + (0 − 0)j + (0 − 0)k = 0. Hence F = ()i + ()j + ()k
is irrotational.
22. divF =
(( )) + (( )) + (( )) = 0 so F is incompressible.
For Exercises 23–29, let F( ) = 1 i + 1 j + 1 k and G( ) = 2 i + 2 j + 2 k.
23. div(F + G) = divh1 + 2 1 + 2 1 + 2i = (1 + 2)
+
(1 + 2)
+
(1 + 2)
=
1
+
2
+
1
+
2
+
1
+
2
= 1 + 1 + 1 + 2 + 2 + 2
= divh1 1 1i + divh2 2 2i = divF + divG
24. curlF + curlG = 1 − 1 i + 1 − 1 j + 1 − 1 k
+ 2 − 2 i + 2 − 2 j + 2 − 2 k
= (1 + 2) − (1 + 2)i + (1 + 2) − (1 + 2)j
+(1 + 2) − (1 + 2)k = curl(F + G)
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.666 ¤ CHAPTER 16 VECTOR CALCULUS
25. div(F) = div( h1 1 1i) = divh1 1 1i = (1)
+
(1)
+
(1)
= 1 + 1 + 1 + 1 + 1 + 1
= 1 + 1 + 1 + h1 1 1i · = divF + F · ∇
26. curl(F) = ( 1) − ( 1)i + ( 1) − ( 1)j + ( 1) − ( 1)k
= 1 + 1 − 1 − 1 i + 1 + 1 − 1 − 1 j
+ 1 + 1 − 1 − 1 k
= 1 − 1 i + 1 − 1 j + 1 − 1 k
+1 − 1 i + 1 − 1 j + 1 − 1 k
= curlF + (∇) × F
27. div(F × G) =∇ · (F × G) =
1 1 1
2 2 2
=
1 1
2 2
−
1 1
2 2
+
1 1
2 2
=1 2 + 2 1 − 2 1 − 1 2 − 1 2 + 2 1 − 2 1 − 1 2
+1 2 + 2 1 − 2 1 − 1 2
=2 1 − 1 + 2 1 − 1 + 2 1 − 1
− 1 2 − 2 + 1 2 − 2 + 1 2 − 2
= G · curlF − F · curlG
28. div(∇ × ∇) = ∇ · curl (∇) − ∇ · curl (∇) [by Exercise 27] = 0 [by Theorem 3]
29. curl(curlF) = ∇ × (∇ × F) =
i j k
1 − 1 1 − 1 1 − 1
= 21 − 221 − 221 + 21 i + 21 − 221 − 221 + 21 j
+ 21 − 221 − 221 + 21 k
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.5 CURL AND DIVERGENCE ¤ 667
Now let’s consider grad(divF) − ∇2F and compare with the above.
(Note that ∇2F is defined on page 1147 [ET 1107].)
grad(divF) − ∇2F = 221 + 21 + 21 i + 21 + 221 + 21 j + 21 + 21 + 221 k
− 221 + 221 + 221 i + 221 + 221 + 221 j
+ 221 + 221 + 221 k
= 21 + 21 − 221 − 221 i + 21 + 21 − 221 − 221 j
+ 21 + 21 − 221 − 222 k
Then applying Clairaut’s Theorem to reverse the order of differentiation in the second partial derivatives as needed and
comparing, we have curl curlF = grad divF − ∇2F as desired.
30. (a) ∇ · r = i + j + k · (i + j + k) = 1 + 1 + 1 = 3
(b) ∇ · (r) = ∇ · 2 + 2 + 2 (i + j + k)
= 2 +2 2 + 2 + 2 + 2 + 2 + 2 +22 + 2 + 2 + 2 + 2
+2 +22 + 2 + 2 + 2 + 2
=
1
2 + 2 + 2 (42 + 42 + 42) = 42 + 2 + 2 = 4
Another method:
By Exercise 25, ∇ · (r) = div(r) = divr + r · ∇ = 3 + r · r
[see Exercise 31(a) below] = 4.
(c) ∇23 = ∇2 2 + 2 + 232
=
3 2(2 + 2 + 2)12(2) + 3 2(2 + 2 + 2)12(2) + 3 2(2 + 2 + 2)12(2)
= 3 1 2(2 + 2 + 2)−12(2)() + (2 + 2 + 2)12
+ 3 1 2(2 + 2 + 2)−12(2)() + (2 + 2 + 2)12
+ 3 1 2(2 + 2 + 2)−12(2)() + (2 + 2 + 2)12
= 3(2 + 2 + 2)−12(42 + 42 + 42) = 12(2 + 2 + 2)12 = 12
Another method:
(2 + 2 + 2)32 = 3 2 + 2 + 2 ⇒ ∇3 = 3(i + j + k) = 3r,
so ∇23 = ∇ · ∇3 = ∇ · (3r) = 3(4) = 12 by part (b).
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.668 ¤ CHAPTER 16 VECTOR CALCULUS
31. (a) ∇ = ∇2 + 2 + 2 = 2 +2 + 2 i + 2 +2 + 2 j + 2 +2 + 2 k = i +2 + j 2++ k2 = r
(b) ∇ × r =
i j k
= () − ()i + () − ()j + () − ()k = 0
(c) ∇ 1 = ∇2 +12 + 2
=
−
1
22 + 2 + 2 (2)
2 + 2 + 2 i −
1
22 + 2 + 2 (2)
2 + 2 + 2 j −
1
22 + 2 + 2 (2)
2 + 2 + 2 k
= −
i + j + k
(2 + 2 + 2)32 = −
r 3
(d) ∇ln = ∇ln(2 + 2 + 2)12 = 1 2∇ln(2 + 2 + 2)
=
2 + 2 + 2 i + 2 + 2 + 2 j + 2 + 2 + 2 k = i2++j2++2k = r2
32. r = i + j + k ⇒ = |r| = 2 + 2 + 2, so
F = r
=
(2 + 2 + 2)2 i + (2 + 2+ 2)2 j + (2 + 2+ 2)2 k
Then
(2 + 2 + 2)2 =
(2 + 2 + 2) − 2
(2 + 2 + 2)1 + 2 =
2 − 2
+ 2 . Similarly,
(2 + 2 + 2)2 =
2 − 2
+ 2 and (2 + 2+ 2)2 = 2− +2 2 . Thus
divF = ∇ · F = 2 − 2
+ 2 +
2 − 2
+ 2 +
2 − 2
+ 2 =
32 − 2 − 2 − 2
+ 2
=
32 − (2 + 2 + 2)
+ 2 =
32 − 2
+ 2 =
3 −
Consequently, if = 3 we have divF = 0.
33. By (13), (∇) · n = div(∇) = [ div(∇) + ∇ · ∇] by Exercise 25. But div(∇) = ∇2.
Hence ∇2 = (∇) · n − ∇ · ∇ .
34. By Exercise 33, ∇2 = (∇) · n − ∇ · ∇ and
∇2 = (∇) · n − ∇ · ∇ . Hence
∇2 − ∇2 = [(∇) · n − (∇) · n] + (∇ · ∇ − ∇ · ∇) = [∇ − ∇ ] · n.
35. Let ( ) = 1. Then ∇ = 0 and Green’s first identity (see Exercise 33) says
∇2 = (∇) · n − 0 · ∇ ⇒ ∇2 = ∇ · n. But is harmonic on , so
∇2 = 0 ⇒ ∇ · n = 0 and n = (∇ · n) = 0.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.5 CURL AND DIVERGENCE ¤ 669
36. Let = . Then Green’s first identity (see Exercise 33) says ∇2 = ()(∇) · n − ∇ · ∇ .
But is harmonic, so ∇2 = 0, and ∇ · ∇ = |∇|2, so we have 0 = ()(∇) · n − |∇|2 ⇒
|∇|2 = ()(∇) · n = 0 since ( ) = 0 on .
37. (a) We know that = , and from the diagram sin = ⇒ = = (sin) = |w × r|. But v is perpendicular
to both w and r, so that v = w × r.
(b) From (a), v = w × r =
i j k
0 0
= (0 · − )i + ( − 0 · )j + (0 · − · 0)k = − i + j
(c) curlv = ∇ × v =
i j k
− 0
= (0) − ()i + (−) − (0)j + () − (−)k
= [ − (−)]k = 2 k = 2w
38. Let H = h1 2 3i and E = h1 2 3i.
(a) ∇ × (∇ × E) = ∇ × (curlE) = ∇ × −1 H = −1
i j k
1 2 3
= −
1
23 − 22 i + 21 − 23 j + 22 − 21 k
= −
1
3 − 2 i + 1 − 3 j + 2 − 1 k [assuming that the partial derivatives are continuous so that the order of differentiation does not matter]
= −
1
curlH = −1 1 E = −12 2E2
(b) ∇ × (∇ × H) = ∇ × (curlH) = ∇ × 1 E = 1
i j k
1 2 3
=
1
23 − 22 i + 21 − 23 j + 22 − 21 k
=
1
3 − 2 i + 1 − 3 j + 2 − 1 k [assuming that the partial derivatives are continuous so that the order of differentiation does not matter]
=
1
curlE = 1 −1 H = −12 2H2
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.670 ¤ CHAPTER 16 VECTOR CALCULUS
(c) Using Exercise 29, we have that curlcurlE = graddivE − ∇2E ⇒
∇2E = graddivE − curlcurlE = grad0 + 1
2
2E
2 [from part (a)] = 12 2E2 .
(d) As in part (c), ∇2H = grad divH − curl curlH = grad 0 + 1
2
2H
2 [using part (b)] = 12 2H2 .
39. For any continuous function on R3, define a vector field G( ) = h( )00i where ( ) = 0 ( ).
Then divG =
(( )) + (0) + (0) = 0 ( ) = ( ) by the Fundamental Theorem of
Calculus. Thus every continuous function on R3 is the divergence of some vector field.
16.6 Parametric Surfaces and Their Areas
1. (4 −51) lies on the parametric surface r( ) = h + − 2 3 + − i if and only if there are values for and
where + = 4, − 2 = −5, and 3 + − = 1. From the first equation we have = 4 − and substituting into the
second equation gives 4 − − 2 = −5 ⇔ = 3. Then = 1, and these values satisfy the third equation, so does lie
on the surface.
(046) lies on r( ) if and only if + = 0, − 2 = 4, and 3 + − = 6, but solving the first two equations
simultaneoulsy gives = 4 3, = − 4 3 and these values do not satisfy the third equation, so does not lie on the surface.
2. (121) lies on the parametric surface r( ) = 1 + − + 2 2 − 2 if and only if there are values for and
where 1 + − = 1, + 2 = 2, and 2 − 2 = 1. From the first equation we have = and substituting into the third
equation gives 0 = 1, an impossibility, so does not lie on the surface.
(233) lies on r( ) if and only if 1 + − = 2, + 2 = 3, and 2 − 2 = 3. From the first equation we have
= + 1 and substituting into the second equation gives + 1 + 2 = 3 ⇔ 2 + − 2 = 0 ⇔ ( + 2)( − 1) = 0,
so = −2 ⇒ = −1 or = 1 ⇒ = 2. The third equation is satisfied by = 2, = 1 so does lie on the
surface.
3. r( ) = ( + )i + (3 − )j + (1 + 4 + 5)k = h031i + h104i + h1 −1 5i. From Example 3, we recognize
this as a vector equation of a plane through the point (031) and containing vectors a = h104i and b = h1 −1 5i. If we
wish to find a more conventional equation for the plane, a normal vector to the plane is a × b =
i j k
1 0 4
1 −1 5
= 4i − j − k
and an equation of the plane is 4( − 0) − ( − 3) − ( − 1) = 0 or 4 − − = −4.
4. r( ) = 2 i + cos j + sin k, so the corresponding parametric equations for the surface are = 2, = cos,
= sin. For any point ( ) on the surface, we have 2 + 2 = 2 cos2 + 2 sin2 = 2 = . Since no restrictions
are placed on the parameters, the surface is = 2 + 2, which we recognize as a circular paraboloid whose axis is the -axis.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.6 PARAMETRIC SURFACES AND THEIR AREAS ¤ 671
5. r( ) = hcos sin i, so the corresponding parametric equations for the surface are = cos, = sin, = .
For any point ( ) on the surface, we have 2 + 2 = 2 cos2 + 2 sin2 = 2 = 2. Since no restrictions are placed on
the parameters, the surface is 2 = 2 + 2, which we recognize as a circular cone with axis the -axis.
6. r( ) = h3cos sini, so the corresponding parametric equations for the surface are = 3cos, = , = sin. For
any point ( ) on the surface, we have (3)2 + 2 = cos2 + sin2 = 1, so vertical cross-sections parallel to the
-plane are all identical ellipses. Since = and −1 ≤ ≤ 1, the surface is the portion of the elliptic cylinder
1 9
2 + 2 = 1 corresponding to −1 ≤ ≤ 1.
7. r( ) = 2 2 + , −1 ≤ ≤ 1, −1 ≤ ≤ 1.
The surface has parametric equations = 2, = 2, = + , −1 ≤ ≤ 1, −1 ≤ ≤ 1.
In Maple, the surface can be graphed by entering
plot3d([uˆ2,vˆ2,u+v],u=-1..1,v=-1..1);.
In Mathematica we use the ParametricPlot3D command.
If we keep constant at 0, = 2 0, a constant, so the
corresponding grid curves must be the curves parallel to the
-plane. If is constant, we have = 02, a constant, so these
grid curves are the curves parallel to the -plane.
8. r( ) = 3 −, −2 ≤ ≤ 2, −2 ≤ ≤ 2.
The surface has parametric equations = , = 3, = −,
−2 ≤ ≤ 2, −2 ≤ ≤ 2. If = 0 is constant,
= 0 = constant, so the corresponding grid curves are the curves
parallel to the -plane. If = 0 is constant, = 03 = constant,
so the corresponding grid curves are the curves parallel to the
-plane.
9. r( ) = 3 sin cos, −1 ≤ ≤ 1, 0 ≤ ≤ 2
The surface has parametric equations = 3, = sin,
= cos, −1 ≤ ≤ 1, 0 ≤ ≤ 2. Note that if = 0 is
constant then = 3 0 is constant and = 0 sin, = 0 cos
describe a circle in , of radius |0|, so the corresponding grid
curves are circles parallel to the -plane. If = 0, a constant,
the parametric equations become = 3, = sin0, = cos0. Then = (tan0), so these are the grid curves we see
that lie in planes = that pass through the -axis.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.672 ¤ CHAPTER 16 VECTOR CALCULUS
10. r( ) = hsin( + ) sini, − ≤ ≤ , − ≤ ≤ .
The surface has parametric equations = , = sin( + ),
= sin, − ≤ ≤ , − ≤ ≤ . If = 0 is constant,
= 0 = constant, so the corresponding grid curves are the
curves parallel to the -plane. If = 0 is constant,
= sin0 = constant, so the corresponding grid curves are the
curves parallel to the -plane.
11. = sin, = cossin4, = sin2sin4, 0 ≤ ≤ 2, − 2 ≤ ≤ 2 .
Note that if = 0 is constant, then = sin0 is constant, so the
corresponding grid curves must be parallel to the -plane. These
are the vertically oriented grid curves we see, each shaped like a
“figure-eight.” When = 0 is held constant, the parametric
equations become = sin, = cos0 sin 4,
= sin 20 sin 4. Since is a constant multiple of , the
corresponding grid curves are the curves contained in planes
= that pass through the -axis.
12. = cos, = sin sin, = cos, 0 ≤ ≤ 2, 0 ≤ ≤ 2.
If = 0 is constant, then = cos 0 = constant, so the
corresponding grid curves are the curves parallel to the -plane. If
= 0 is constant, then = cos0 = constant, so the
corresponding grid curves are the curves parallel to the -plane.
13. r( ) = cos i+ sinj + k. The parametric equations for the surface are = cos, = sin, = . We look at
the grid curves first; if we fix , then and parametrize a straight line in the plane = which intersects the -axis. If is
held constant, the projection onto the -plane is circular; with = , each grid curve is a helix. The surface is a spiraling
ramp, graph IV.
14. r( ) = 2 i + 2 j + (2 − 2)k. The parametric equations for the surface are = 2, = 2, = 2 − 2. If
= 0 is held constant, then = 02, = 2 0 so = 0(2 0)2 = (13 0)2, and = 2 0 − 2 = 2 0 − (10). Thus
each grid curve corresponding to = 0 lies in the plane = 2 0 − (10) and its projection onto the -plane is a parabola
= 2 with axis the -axis. Similarly, if = 0 is held constant, then = 02, = 20 ⇒
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.6 PARAMETRIC SURFACES AND THEIR AREAS ¤ 673
= (02)20 = (103)2, and = 2 − 02 = (10) − 02. Each grid curve lies in the plane = (10) − 02 and its
projection onto the -plane is a parabola = 2 with axis the -axis. The surface is graph VI.
15. r( ) = (3 − )i + 2 j + 2 k. The parametric equations for the surface are = 3 − , = 2, = 2. If we fix
then and are constant so each corresponding grid curve is contained in a line parallel to the -axis. (Since = 2 ≥ 0, the
grid curves are half-lines.) If is held constant, then = 2 = constant, so each grid curve is contained in a plane parallel to
the -plane. Since and are functions of only, the grid curves all have the same shape. The surface is the cylinder shown
in graph I.
16. = (1 − )(3 + cos )cos4, = (1 − )(3 + cos)sin4, = 3 + (1 − )sin. These equations correspond to
graph V: when = 0, then = 3 + cos, = 0, and = sin, which are equations of a circle with radius 1 in the -plane
centered at (300). When = 1 2 , then = 3 2 + 1 2 cos, = 0, and = 3 2 + 1 2 sin, which are equations of a circle with
radius 1
2 in the -plane centered at 3 2 0 3 2 . When = 1, then = = 0 and = 3, giving the topmost point shown in the
graph. This suggests that the grid curves with constant are the vertically oriented circles visible on the surface. The spiralling
grid curves correspond to keeping constant.
17. = cos3 cos3 , = sin3 cos3 , = sin3 . If = 0 is held constant then = sin3 0 is constant, so the
corresponding grid curve lies in a horizontal plane. Several of the graphs exhibit horizontal grid curves, but the curves for this
surface are neither ellipses nor straight lines, so graph III is the only possibility. (In fact, the horizontal grid curves here are
members of the family = cos3 , = sin3 and are called astroids.) The vertical grid curves we see on the surface
correspond to = 0 held constant, as then we have = cos3 0 cos3 , = sin3 0 cos3 so the corresponding grid curve
lies in the vertical plane = (tan3 0) through the -axis.
18. = sin, = cos sin, = sin. If = 0 is fixed, then = sin0 is constant, and = sin, = (sin0)cos
describe an ellipse that is contained in the horizontal plane = sin0. If = 0 is fixed, then = sin0 is constant, and
= (cos 0)sin, = sin ⇒ = (cos 0), so the grid curves are portions of lines through the -axis contained in
the plane = sin0 (parallel to the -plane). The surface is graph II.
19. From Example 3, parametric equations for the plane through the point (0 00) that contains the vectors a = h1 −10i and
b = h01 −1i are = 0 + (1) + (0) = , = 0 + (−1) + (1) = − , = 0 + (0) + (−1) = −.
20. From Example 3, parametric equations for the plane through the point (0 −15) that contains the vectors a = h214i and
b = h−3 2 5i are = 0 + (2) + (−3) = 2 − 3, = −1 + (1) + (2) = −1 + + 2,
= 5 + (4) + (5) = 5 + 4 + 5.
21. Solving the equation for gives 2 = 1 + 2 + 1 4 2 ⇒ = 1 + 2 + 1 4 2. (We choose the positive root since we want
the part of the hyperboloid that corresponds to ≥ 0.) If we let and be the parameters, parametric equations are = ,
= , = 1 + 2 + 1 4 2.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.674 ¤ CHAPTER 16 VECTOR CALCULUS
22. Solving the equation for gives 2 = 1 2(1 − 2 − 32) ⇒ = − 1 2(1 − 2 − 32) (since we want the part of the
ellipsoid that corresponds to ≤ 0). If we let and be the parameters, parametric equations are = , = ,
= − 1 2(1 − 2 − 32).
Alternate solution: The equation can be rewritten as 2 + 1√222 + (1√23)2 = 1, and if we let = cos and
=
1 √
3
sin, then = − 1 2(1 − 2 − 32) = − 1 2(1 − 2 cos2 − 2 sin2 ) = − 1 2(1 − 2), where 0 ≤ ≤ 1
and 0 ≤ ≤ 2.
Second alternate solution: We can adapt the formulas for converting from spherical to rectangular coordinates as follows.
We let = sincos, = √12 sinsin, = √13 cos; the surface is generated for 0 ≤ ≤ , ≤ ≤ 2.
23. Since the cone intersects the sphere in the circle 2 + 2 = 2, = √2 and we want the portion of the sphere above this, we
can parametrize the surface as = , = , = 4 − 2 − 2 where 2 + 2 ≤ 2.
Alternate solution: Using spherical coordinates, = 2sincos, = 2sinsin, = 2cos where 0 ≤ ≤ 4 and
0 ≤ ≤ 2.
24. We can parametrize the cylinder as = 3 cos, = , = 3 sin. To restrict the surface to that portion above the -plane
and between the planes = −4 and = 4 we require 0 ≤ ≤ , −4 ≤ ≤ 4.
25. In spherical coordinates, parametric equations are = 6 sincos, = 6 sinsin, = 6 cos. The intersection of the
sphere with the plane = 3√3 corresponds to = 6 cos = 3√3 ⇒ cos = √23 ⇒ = 6 , and the plane = 0
(the -plane) corresponds to = 2 . Thus the surface is described by 6 ≤ ≤ 2 , 0 ≤ ≤ 2.
26. Using and as the parameters, = , = , = + 3 where 0 ≤ 2 + 2 ≤ 1. Also, since the plane intersects the
cylinder in an ellipse, the surface is a planar ellipse in the plane = + 3. Thus, parametrizing with respect to and , we
have = cos , = sin, = 3 + cos where 0 ≤ ≤ 1 and 0 ≤ ≤ 2.
27. The surface appears to be a portion of a circular cylinder of radius 3 with axis the -axis. An equation of the cylinder is
2 + 2 = 9, and we can impose the restrictions 0 ≤ ≤ 5, ≤ 0 to obtain the portion shown. To graph the surface on a
CAS, we can use parametric equations = , = 3 cos , = 3 sin with the parameter domain 0 ≤ ≤ 5, 2 ≤ ≤ 32 .
Alternatively, we can regard and as parameters. Then parametric equations are = , = , = −√9 − 2, where
0 ≤ ≤ 5 and −3 ≤ ≤ 3.
28. The surface appears to be a portion of a sphere of radius 1 centered at the origin. In spherical coordinates, the sphere has
equation = 1, and imposing the restrictions 2 ≤ ≤ 2, 4 ≤ ≤ will give only the portion of the sphere shown. Thus,
to graph the surface on a CAS we can either use spherical coordinates with the stated restrictions, or we can use parametric
equations: = sincos, = sinsin, = cos, 2 ≤ ≤ 2, 4 ≤ ≤ .
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.6 PARAMETRIC SURFACES AND THEIR AREAS ¤ 675
29. Using Equations 3, we have the parametrization = ,
=
1
1 + 2 cos, = 1 +12 sin, −2 ≤ ≤ 2, 0 ≤ ≤ 2.
30. Letting be the angle of rotation about the -axis (adapting
Equations 3), we have the parametrization = (1)cos, = ,
= (1)sin, ≥ 1, 0 ≤ ≤ 2.
31. (a) Replacing cos by sin and sin by cos gives parametric equations
= (2 + sin)sin, = (2 + sin)cos, = + cos. From the graph, it
appears that the direction of the spiral is reversed. We can verify this observation by
noting that the projection of the spiral grid curves onto the -plane, given by
= (2 + sin)sin, = (2 + sin)cos, = 0, draws a circle in the clockwise
direction for each value of . The original equations, on the other hand, give circular
projections drawn in the counterclockwise direction. The equation for is identical in
both surfaces, so as increases, these grid curves spiral up in opposite directions for
the two surfaces.
(b) Replacing cos by cos 2 and sin by sin 2 gives parametric equations
= (2 + sin)cos 2, = (2 + sin)sin2, = + cos . From the graph, it
appears that the number of coils in the surface doubles within the same parametric
domain. We can verify this observation by noting that the projection of the spiral grid
curves onto the -plane, given by = (2 + sin)cos 2, = (2 + sin)sin2,
= 0 (where is constant), complete circular revolutions for 0 ≤ ≤ while the
original surface requires 0 ≤ ≤ 2 for a complete revolution. Thus, the new
surface winds around twice as fast as the original surface, and since the equation for
is identical in both surfaces, we observe twice as many circular coils in the same
-interval.
32. First we graph the surface as viewed from the front, then from two additional viewpoints.
The surface appears as a twisted sheet, and is unusual because it has only one side. (The Möbius strip is discussed in more
detail in Section 16.7.)
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.676 ¤ CHAPTER 16 VECTOR CALCULUS
33. r( ) = ( + )i + 32 j + ( − )k.
r = i + 6j + k and r = i − k, so r × r = −6i + 2j − 6k. Since the point (230) corresponds to = 1, = 1, a
normal vector to the surface at (230) is −6i + 2j − 6k, and an equation of the tangent plane is −6 + 2 − 6 = −6 or
3 − + 3 = 3.
34. r( ) = (2 + 1)i + (3 + 1)j + ( + )k.
r = 2i + k and r = 32 j + k, so r × r = −32 i − 2j + 62 k. Since the point (523) corresponds to = 2,
= 1, a normal vector to the surface at (523) is −3i − 4j + 12k, and an equation of the tangent plane is
−3( − 5) − 4( − 2) + 12( − 3) = 0 or 3 + 4 − 12 = −13.
35. r( ) = cos i + sinj + k ⇒ r1 3 = 1 2 √23 3 .
r = cosi + sin j and r = −sin i + cos j + k, so a normal vector to the surface at the point 1 2 √23 3 is
r1 3 × r1 3 = 1 2 i + √23 j × − √23 i + 1 2 j + k = √23 i − 1 2 j + k. Thus an equation of the tangent plane at
1 2 √23 3 is √23 − 1 2 − 1 2 − √23 + 1 − 3 = 0 or √23 − 1 2 + = 3 .
36. r( ) = sini + cos sinj + sin k ⇒ r 6 6 = 1 2 √43 1 2 .
r = cosi − sinsin j and r = coscos j + cosk, so a normal vector to the surface at the point 1 2 √43 1 2 is
r 6 6 × r 6 6 = √23 i − 1 4 j × 3 4 j + √23 k = − √83 i − 3 4 j + 3√8 3 k.
Thus an equation of the tangent plane at 1 2 √43 1 2 is − √83 − 1 2 − 3 4 − √43 + 3√8 3 − 1 2 = 0 or
√3 + 6 − 3√3 = √23 or 2 + 4√3 − 6 = 1.
37. r( ) = 2 i + 2sinj + cos k ⇒ r(10) = (1 0 1).
r = 2i + 2 sinj + cos k and r = 2cos j − sin k,
so a normal vector to the surface at the point (101) is
r(1 0) × r(1 0) = (2i + k) × (2j) = −2i + 4k.
Thus an equation of the tangent plane at (101) is
−2( − 1) + 0( − 0) + 4( − 1) = 0 or − + 2 = 1.
38. r( ) = (1 − 2 − 2)i − j − k.
r = −2i − k and r = −2i − j. Since the point (−1 −1 −1)
corresponds to = 1, = 1, a normal vector to the surface at
(−1 −1 −1) is
r(1 1) × r(1 1) = (−2i − k) × (−2i − j) = −i + 2j + 2k.
Thus an equation of the tangent plane is −1( + 1) + 2( + 1) + 2( + 1) = 0 or − + 2 + 2 = −3.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.6 PARAMETRIC SURFACES AND THEIR AREAS ¤ 677
39. The surface is given by = ( ) = 6 − 3 − 2 which intersects the -plane in the line 3 + 2 = 6, so is the
triangular region given by ( ) 0 ≤ ≤ 2 0 ≤ ≤ 3 − 3 2. By Formula 9, the surface area of is
() = 1 + 2 + 2
= 1 + (−3)2 + (−2)2 = √14 = √14() = √14 1 2 · 2 · 3 = 3√14
40. r( ) = h + 2 − 31 + − i ⇒ r = h1 −31i, r = h10 −1i, and r × r = h323i. Then by
Definition 6,
() = |r × r | = 02−11 | h323i | = √2202 −11 = √22 (2)(2) = 4√22
41. Here we can write = ( ) = 1 3 − 1 3 − 2 3 and is the disk 2 + 2 ≤ 3, so by Formula 9 the area of the surface is
() = 1 + 2 + 2 = 1 + − 1 32 + − 2 32 = √314
=
√14
3 () = √314 · √32 = √14
42. = ( ) = 2 + 2 ⇒
=
1 2
2 + 2−12 · 2 = 2+ 2 , = 2+ 2 , and
1 + 2 + 2 = 1 + 2+2 2 + 2 +2 2 = 1 + 2 2 + + 2 2 = √2
Here is given by ( ) 0 ≤ ≤ 1 2 ≤ ≤ , so by Formula 9, the surface area of is
() = √2 = 012 √2 = √201 − 2 = √2 1 22 − 1 331 0 = √2 1 2 − 1 3 = √62
43. = ( ) = 2 3(32 + 32) and = {( )|0 ≤ ≤ 1 0 ≤ ≤ 1}. Then = 12, = 12 and
() = 1 + (√)2 + √ 2 = 01 01 √1 + +
= 01 2 3( + + 1)32 =1 =0 = 2 3 01 ( + 2)32 − ( + 1)32
=
2 3
2 5( + 2)52 − 2 5( + 1)521 0 = 15 4 (352 − 252 − 252 + 1) = 15 4 (352 − 272 + 1)
44. = ( ) = 4 − 22 + and = {( )|0 ≤ ≤ 1 0 ≤ ≤ }. Thus, by Formula 9,
() = 1 + (−4)2 + (1)2 = 01 0 √162 + 2 = 01 √162 + 2
=
1
32 ·
2 3
(162 + 2)321 0 = 48 1 (1832 − 232) = 48 1 (54√2 − 2√2) = 13 12√2
45. = ( ) = with 2 + 2 ≤ 1, so = , = ⇒
() = 1 + 2 + 2 = 0201 √2 + 1 = 02 1 3 (2 + 1)32 =1 =0
= 02 1 32√2 − 1 = 232√2 − 1
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.678 ¤ CHAPTER 16 VECTOR CALCULUS
46. A parametric representation of the surface is = 2 + , = , = with 0 ≤ ≤ 2, 0 ≤ ≤ 2.
Hence r
× r = (i + j) × (2 i + k) = i − j − 2 k.
Then
() = |r × r | = 0202 √1 + 1 + 42 = 02 2√2 + 42
= 2 · 1 2 √2 + 42 + ln2 + √2 + 42 2 0 or Formula 21 in the Table of Integrals Use trigonometric substitution
= 6√2 + ln4 + 3√2 − ln√2 or 6√2 + ln 4 + 3 √2√2 = 6√2 + ln2√2 + 3
Note: In general, if = ( ) then r × r = i −
j − k and () = 1 + 2 + 2 .
47. A parametric representation of the surface is = , = 2 + 2, = with 0 ≤ 2 + 2 ≤ 16.
Hence r × r = (i + 2j) × (2 j + k) = 2i − j + 2 k.
Note: In general, if = ( ) then r × r =
i − j + k, and () = 1 + 2 + 2 . Then
() =
0 ≤ 2 + 2 ≤ 16
√1 + 42 + 42 = 0204 √1 + 42
= 02 04 √1 + 42 = 2 12 1 (1 + 42)324 0 = 6 6532 − 1
48. r = hcos sin0i, r = h−sin cos1i, and r × r = hsin −cos i. Then
() = 001 √1 + 2 = 0 01 √1 + 2
= 2 √2 + 1 + 1 2 ln + √2 + 1 1 0 = 2 √2 + ln1 + √2
49. r = h2 0i, r = h0 i, and r × r = 2 −222. Then
() = |r × r| = 0102 √4 + 422 + 44 = 0102 (2 + 22)2
= 0102 (2 + 22) = 01 1 33 + 22 =2 =0 = 01 8 3 + 42 = 8 3 + 4 331 0 = 4
50. The cylinder encloses separate portions of the sphere in the upper and lower halves. The top half of the sphere is
= ( ) = 2 − 2 − 2 and is given by ( ) 2 + 2 ≤ 2. By Formula 9, the surface area of the upper
enclosed portion is
=
1 + 2 −−2 − 2 2 + 2 −−2 − 2 2 = 1 + 2 −2 +2 −2 2
= 2 − 22 − 2 = 020 √ 2− 2 = 02 0 √ 2− 2
= 2 0 −√ 2 − 2 0 = 2−√ 2 − 2 + √ 2 − 0 = 2 − √ 2 − 2
The lower portion of the sphere enclosed by the cylinder has identical shape, so the total area is 2 = 4 − √ 2 − 2.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.6 PARAMETRIC SURFACES AND THEIR AREAS ¤ 679
51. From Equation 9 we have () = 1 + ()2 + ()2 . But if || ≤ 1 and || ≤ 1 then 0 ≤ ()2 ≤ 1,
0 ≤ ()2 ≤ 1 ⇒ 1 ≤ 1 + ()2 + ()2 ≤ 3 ⇒ 1 ≤ 1 + ()2 + ()2 ≤ √3. By Property 15.2.11,
1 ≤ 1 + ()2 + ()2 ≤ √3 ⇒ () ≤ () ≤ √3() ⇒
2 ≤ () ≤ √32.
52. = ( ) = cos(2 + 2) with 2 + 2 ≤ 1.
() = 1 + (−2sin(2 + 2))2 + (−2 sin(2 + 2))2
= 1 + 42 sin2(2 + 2) + 42 sin2(2 + 2) = 1 + 4(2 + 2)sin2(2 + 2)
= 02 01 1 + 42 sin2(2) = 02 01 1 + 42 sin2(2)
= 2 01 1 + 42 sin2(2) ≈ 41073
53. = ( ) = ln(2 + 2 + 2) with 2 + 2 ≤ 1.
() = 1 + 2 +22 + 22 + 2 +22 + 22 = 1 + (24+2 + 4 2 + 2) 2 2
= 02 01 1 + (24+ 2) 2 2 = 02 01 (2(+ 2) 2 + 2) 2 + 4 2 2 = 2 01 √4+ 8 2 + 2 2 + 4 ≈ 35618
54. Let ( ) = 1 + 2
1 + 2 . Then = 1 +22 ,
= (1 + 2)−(1 +22)2 = −2(1 + (1 +2)22).
We use a CAS to estimate
−11 −1(1 − −||||) 1 + 2 + 2 ≈ 26959.
In order to graph only the part of the surface above the square, we
use −(1 − ||) ≤ ≤ 1 − || as the -range in our plot command.
55. (a) () = 1 + 2 + 2 = 0604 1 + (1 + 422+ 4 +22)4 .
Using the Midpoint Rule with ( ) = 1 + (1 + 422+ 4 +22)4 , = 3, = 2 we have
() ≈
3
= 1
2
= 1
∆ = 4 [(11) + (13) + (3 1) + (3 3) + (51) + (53)] ≈ 242055
(b) Using a CAS we have () = 06 04 1 + (1 + 422+ 4 +22)4 ≈ 242476. This agrees with the estimate in part (a)
to the first decimal place.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.680 ¤ CHAPTER 16 VECTOR CALCULUS
56. r( ) = cos3 cos3 sin3 cos3 sin3 , so r = −3cos2 sincos3 3sin2 coscos3 0,
r = −3cos3 cos2 sin −3sin3 cos2 sin 3sin2 cos, and
r × r = 9cos sin2 cos4 sin2 9cos2 sin cos4 sin2 9cos2 sin2 cos5 sin. Then
|r × r| = 9cos2 sin4 cos8 sin4 + cos4 sin2 cos8 sin4 + cos4 sin4 cos10 sin2
= 9cos2 sin2 cos8 sin2 (sin2 + cos2 sin2 cos2 )
= 9 cos4 |cos sin sin| sin2 + cos2 sin2 cos2
Using a CAS, we have () = 0 02 9cos4 |cos sin sin| sin2 + cos2 sin2 cos2 ≈ 44506.
57. = 1 + 2 + 3 + 42, so
() = 1 + 2 + 2 = 14 01 1 + 4 + (3 + 8)2 = 14 01 14 + 48 + 642 .
Using a CAS, we have
14 01 14 + 48 + 642 = 45 8 √14 + 15 16 ln11√5 + 3√14 √5 − 15 16 ln3√5 + √14 √5
or 45
8 √14 + 15 16 ln 11 3 √ √5 + 3 5 + √√70 70 .
58. (a) r = cos i + sinj + 2k, r = −sin i + cos j + 0k, and
r × r = −22 cos i − 22 sin j + k.
() = 0202 |r × r| = 0202 424 cos2 + 424 sin2 + 222
(b) 2 = 22 cos2 , 2 = 22 sin2 , = 2 ⇒ 22 + 22 = 2 = which is an elliptic paraboloid. To find ,
notice that 0 ≤ ≤ 2 ⇒ 0 ≤ ≤ 4 ⇒ 0 ≤ 22 + 22 ≤ 4. Therefore, using Formula 9, we have
() = −22 −√√44−−((22 22)) 1 + (22)2 + (22)2 .
(c) (d) We substitute = 2, = 3 in the integral in part (a) to get
() = 0202 292 cos2 + 42 sin2 + 9 . We use a CAS
to estimate the integral accurate to four decimal places. To speed up the
calculation, we can set Digits:=7; (in Maple) or use the approximation
command N (in Mathematica). We find that () ≈ 1156596.
59. (a) = sincos, = sinsin, = cos ⇒
2
2 +
2
2 +
2
2 = (sincos)2 + (sinsin)2 + (cos)2
= sin2 + cos2 = 1
and since the ranges of and are sufficient to generate the entire graph,
the parametric equations represent an ellipsoid.
(b)
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.6 PARAMETRIC SURFACES AND THEIR AREAS ¤ 681
(c) From the parametric equations (with = 1, = 2, and = 3),
we calculate r = coscos i + 2 cossin j − 3sink and
r = −sinsini + 2 sincos j. So r × r = 6 sin2 cos i + 3sin2 sin j + 2sincos k, and the surface
area is given by () = 020 |r × r| = 020 36 sin4 cos2 + 9 sin4 sin2 + 4 cos2 sin2
60. (a) = cosh cos, = cosh sin, = sinh ⇒
2
2 +
2
2 −
2
2 = cosh2 cos2 + cosh2 sin2 − sinh2
= cosh2 − sinh2 = 1
and the parametric equations represent a hyperboloid of
one sheet.
(b)
(c) r = sinh cos i + 2 sinh sin j + 3 coshk and
r = −cosh sin i + 2 cosh cos j, so r × r = −6cosh2 cos i − 3cosh2 sin j + 2 cosh sinhk.
We integrate between = sinh−1(−1) = −ln1 + √2 and = sinh−1 1 = ln1 + √2, since then varies between
−3 and 3, as desired. So the surface area is
() = 02−lnln((1 + 1 +√√22)) |r × r|
= 02−lnln((1 + 1 +√√22)) 36 cosh4 cos2 + 9 cosh4 sin2 + 4 cosh2 sinh2
61. To find the region : = 2 + 2 implies + 2 = 4 or 2 − 3 = 0. Thus = 0 or = 3 are the planes where the
surfaces intersect. But 2 + 2 + 2 = 4 implies 2 + 2 + ( − 2)2 = 4, so = 3 intersects the upper hemisphere.
Thus ( − 2)2 = 4 − 2 − 2 or = 2 + 4 − 2 − 2. Therefore is the region inside the circle 2 + 2 + (3 − 2)2 = 4,
that is, = ( ) | 2 + 2 ≤ 3.
() = 1 + [(−)(4 − 2 − 2)−12]2 + [(−)(4 − 2 − 2)−12]2
= 02 0√3 1 + 4 −22 = 02 0√3 √24 − 2 = 02 −2(4 − 2)12 = =0√3
= 02(−2 + 4) = 22 0 = 4
62. We first find the area of the face of the surface that intersects the positive -axis. A parametric representation of the surface is
= , = √1 − 2, = with 2 + 2 ≤ 1. Then r( ) = √1 − 2 ⇒ r = h100i,
r = 0 −√1 − 21 and r × r = 0 −1 −√1 − 2 ⇒ |r × r | = 1 + 1 −22 = √11− 2 .
() =
2+2≤1
|r × r | = −11 −√√11−−22 √11− 2 = 401 0√1−2 √1 1− 2 by the symmetry of the surface
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.682 ¤ CHAPTER 16 VECTOR CALCULUS
This integral is improper [when = 1], so
() = lim
→1−
40 0√1−2 √1 1− 2 = lim →1− 40 √ √1 1 − − 2 2 = lim →1− 40 = lim →1− 4 = 4
Since the complete surface consists of four congruent faces, the total surface area is 4(4) = 16.
Alternate solution: The face of the surface that intersects the positive -axis can also be parametrized as
r( ) = hcossini for − 2 ≤ ≤ 2 and 2 + 2 ≤ 1 ⇔ 2 + sin2 ≤ 1 ⇔
−1 − sin2 ≤ ≤ 1 − sin2 ⇔ −cos ≤ ≤ cos. Then r = h100i, r = h0 −sincos i and
r × r = h0 −cos −sini ⇒ |r × r | = 1, so
() = − 22 −cos cos 1 = − 22 2cos = 2 sin − 2 2 = 4. Again, the area of the complete surface
is 4(4) = 16.
63. Let (1) be the surface area of that portion of the surface which lies above the plane = 0. Then () = 2(1).
Following Example 10, a parametric representation of 1 is = sincos, = sinsin,
= cos and |r × r| = 2 sin. For , 0 ≤ ≤ 2 and for each fixed , − 1 2 2 + 2 ≤ 1 2 2 or
sincos − 1 2 2 + 2 sin2 sin2 ≤ (2)2 implies 2 sin2 − 2 sincos ≤ 0 or
sin(sin − cos) ≤ 0. But 0 ≤ ≤ 2 , so cos ≥ sin or sin 2 + ≥ sin or − 2 ≤ ≤ 2 − .
Hence = ( ) | 0 ≤ ≤ 2 , − 2 ≤ ≤ 2 − . Then
(1) = 02( − (2) −2) 2 sin = 2 02 ( − 2)sin
= 2 [(− cos) − 2(−cos + sin)] 0 2 = 2( − 2)
Thus () = 22( − 2).
Alternate solution: Working on 1 we could parametrize the portion of the sphere by = , = , = 2 − 2 − 2.
Then |r × r| = 1 + 2 − 2 2 − 2 + 2 − 22 − 2 = 2 −2 − 2 and
(1) =
0 ≤ ( − (2))2 + 2 ≤ (2)2
2 − 2 − 2 = − 22 0 cos √2− 2
= − 22 −(2 − 2)12 = = 0 cos = − 22 2[1 − (1 − cos2 )12]
= − 22 2(1 − |sin|) = 22 02(1 − sin) = 22 2 − 1
Thus () = 42 2 − 1 = 22( − 2).
Notes:
(1) Perhaps working in spherical coordinates is the most obvious approach here. However, you must be careful
in setting up .
(2) In the alternate solution, you can avoid having to use |sin| by working in the first octant and then
multiplying by 4. However, if you set up 1 as above and arrived at (1) = 2, you now see your error.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.6 PARAMETRIC SURFACES AND THEIR AREAS ¤ 683
64. (a) Here = sin, = ||, and = ||. But
|| = || + || = + cos and sin = ||
|| so that
= || sin = ( + cos)sin. Similarly cos = ||
|| so
= ( + cos)cos. Hence a parametric representation for the
torus is = cos + cos cos, = sin + cos sin,
= sin, where 0 ≤ ≤ 2, 0 ≤ ≤ 2.
(b)
= 1, = 8 = 3, = 8
= 3, = 4
(c) = cos + cos cos, = sin + cos sin, = sin, so r = h−sin cos −sin sin cosi,
r = h−( + cos)sin( + cos)cos0i and
r × r = −cos cos − 2 cos cos2 i + −sin cos − 2 sin cos2 j
+−cos2 sin − 2 cos2 sin cos − sin2 sin − 2 sin2 sin cosk
= −( + cos)[(cos cos)i + (sin cos)j + (sin)k]
Then |r × r| = ( + cos)cos2 cos2 + sin2 cos2 + sin2 = ( + cos).
Note: , −1 ≤ cos ≤ 1 so | + cos| = + cos. Hence
() = 0202 ( + cos) = 2 + 2 sin2 0 = 42.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.684 ¤ CHAPTER 16 VECTOR CALCULUS
16.7 Surface Integrals
1. The box is a cube where each face has surface area 4. The centers of the faces are (±1 0 0), (0 ±10), (0 0 ±1). For each
face we take the point ∗ to be the center of the face and ( ) = cos( + 2 + 3), so by Definition 1,
( ) ≈ [(100)](4) + [(−100)](4) + [(010)](4)
+ [(0 −10)](4) + [(0 0 1)](4) + [(00 −1)](4)
= 4 [cos 1 + cos(−1) + cos 2 + cos(−2) + cos 3 + cos(−3)] ≈ −693
2. Each quarter-cylinder has surface area 1 4[2(1)(2)] = and the top and bottom disks have surface area (1)2 = . We can
take (001) as a sample point in the top disk, (00 −1) in the bottom disk, and (±100), (0 ±10) in the four
quarter-cylinders. Then ( ) can be approximated by the Riemann sum
(1 0 0)() + (−1 00)() + (010)() + (0 −10)() + (0 0 1)() + (00 −1)()
= (2 + 2 + 3 + 3 + 4 + 4) = 18 ≈ 565.
3. We can use the - and -planes to divide into four patches of equal size, each with surface area equal to 1 8 the surface
area of a sphere with radius √50, so ∆ = 1 8(4)√502 = 25. Then (±3 ±45) are sample points in the four patches,
and using a Riemann sum as in Definition 1, we have
( ) ≈ (345)∆ + (3 −4 5)∆ + (−345)∆ + (−3 −4 5)∆
= (7 + 8 + 9 + 12)(25) = 900 ≈ 2827
4. On the surface, ( ) = 2 + 2 + 2 = (2) = −5. So since the area of a sphere is 42,
( ) = (2) = −5 = −5[4(2)2] = −80.
5. r( ) = ( + )i + ( − )j + (1 + 2 + )k, 0 ≤ ≤ 2, 0 ≤ ≤ 1 and
r ×r = (i + j + 2k) × (i − j + k) = 3i+j− 2k ⇒ |r × r| = 32 + 12 + (−2)2 = √14. Then by Formula 2,
( + + ) = ( + + − + 1 + 2 + ) |r × r| = 01 02(4 + + 1) · √14
= √1401 22 + + =2 =0 = √1401 (2 + 10) = √142 + 101 0 = 11√14
6. r( ) = cosi + sinj + k, 0 ≤ ≤ 1, 0 ≤ ≤ 2 and
r × r = (cos i + sinj + k) × (−sin i + cos j) = −cosi − sin j + k ⇒
|r × r| = 2 cos2 + 2 sin2 + 2 = √22 = √2 [since ≥ 0]. Then by Formula 2,
= (cos)(sin)() |r × r| = 01 02(3 sin cos) · √2
= √201 4 02 sin cos = √2 1 551 0 1 2 sin2 0 2 = √2 · 1 5 · 1 2 = 10 1 √2
7. r( ) = hcos sin i, 0 ≤ ≤ 1, 0 ≤ ≤ and
r × r = hcos sin0i × h−sin cos1i = hsin −cos i ⇒
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.7 SURFACE INTEGRALS ¤ 685
|r × r| = sin2 + cos2 + 2 = √2 + 1. Then
= (sin) |r × r| = 01 0(sin) · √2 + 1 = 01 √2 + 1 0 sin
= 1 3(2 + 1)321 0 [−cos] 0 = 1 3(232 − 1) · 2 = 2 3(2√2 − 1)
8. r( ) = 2 2 − 2 2 + 2, 2 + 2 ≤ 1 and
r × r = h22 2i × h2 −22i = 842 − 42 −42 − 42, so
|r × r| = (8)2 + (42 − 42)2 + (−42 − 42)2 = √6422 + 324 + 324
= 32(2 + 2)2 = 4√2(2 + 2)
Then
(2 + 2) = (2)2 + (2 − 2)2 |r × r| = (422 + 4 − 222 + 4) · 4√2(2 + 2)
= 4√2(4 + 222 + 4)(2 + 2) = 4√2(2 + 2)3 = 4√202 01(2)3
= 4√202 01 7 = 4√2 2 0 1 8 81 0 = 4√2 · 2 · 1 8 = √2
9. = 1 + 2 + 3 so
= 2 and = 3. Then by Formula 4,
2 = 2 2 + 2 + 1 = 03 02 2(1 + 2 + 3)√4 + 9 + 1
= √1403 02(2 + 23 + 322) = √1403 1 2 22 + 32 + 23 =2 =0
= √1403(102 + 43) = √14 10 3 3 + 43 0 = 171√14
10. is the part of the plane = 4 − 2 − 2 over the region = {( ) | 0 ≤ ≤ 2 0 ≤ ≤ 2 − }. Thus
= (4 − 2 − 2)(−2)2 + (−2)2 + 1 = 302 02− 4 − 22 − 2
= 302 4 − 22 − 2 =2 =0− = 302 4(2 − ) − 22(2 − ) − (2 − )2
= 302 3 − 42 + 4 = 3 1 4 4 − 4 3 3 + 222 0 = 34 − 32 3 + 8 = 4
11. An equation of the plane through the points (1 0 0), (0 −20), and (004) is 4 − 2 + = 4, so is the region in the
plane = 4 − 4 + 2 over = {( ) | 0 ≤ ≤ 1 2 − 2 ≤ ≤ 0}. Thus by Formula 4,
= (−4)2 + (2)2 + 1 = √21 01 20−2 = √21 01 [] =0 =2−2
= √21 01(−22 + 2) = √21− 2 3 3 + 21 0 = √21− 2 3 + 1 = √321
12. = 2
3(32 + 32) and
= (√)2 + √ 2 + 1 = 01 01 √ + + 1
= 01 2 3( + + 1)32 =1 =0 = 01 23 ( + 2)32 − ( + 1)32
[continued]
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.686 ¤ CHAPTER 16 VECTOR CALCULUS
Substituting = + 2 in the first term and = + 1 in the second, we have
= 2 3 23( − 2)32 − 2 3 12( − 1)32 = 2 3 2 772 − 4 5523 2 − 2 3 2 772 − 2 5522 1
=
2 3
2 7(372 − 272) − 4 5(352 − 252) − 2 7(272 − 1) + 2 5(252 − 1)
=
2 3
18 35 √3 + 35 8 √2 − 35 4 = 105 4 9√3 + 4√2 − 2
13. Using and as parameters, we have r( ) = (2 + 2)i + j + k, 2 + 2 ≤ 1. Then
r
× r = (2i + j) × (2 i + k) = i − 2j − 2 k and |r × r| = 1 + 42 + 42 = 1 + 4(2 + 2). Thus
2 =
2+2≤1
21 + 4(2 + 2) = 02 01( sin)2 √1 + 42
= 02 sin2 01 3 √1 + 42 let = 1 + 42 ⇒ 2 = 1 4( − 1) and = 1 8
= 1 2 − 1 4 sin 22 0 15 1 4( − 1)√ · 1 8 = · 32 1 15(32 − 12) = 32 1 2 552 − 2 3325 1
=
1
32 2 5(5)52 − 2 3(5)32 − 2 5 + 2 3 = 32 1 20 3 √5 + 15 4 = 120 1 25√5 + 1
14. Using and as parameters, we have r( ) = i + √2 + 2 j + k, 2 + 2 ≤ 25. Then
r × r = i + √2+ 2 j × √2+ 2 j + k = √2+ 2 i − j + √2+ 2 k and
|r × r| = 2+2 2 + 1 + 2 +2 2 = 2 2 + + 2 2 + 1 = √2. Thus
22 =
2+2≤25
(2 + 2)2√2 = √202 05 2( sin)2
= √202 sin2 05 5 = √2 1 2 − 1 4 sin 22 0 1 665 0
= √2() · 1 6(15,625 − 0) = 15,625 6 √2
15. Using and as parameters, we have r( ) = i + (2 + 4)j + k, 0 ≤ ≤ 1, 0 ≤ ≤ 1. Then
r × r = (i + 2j) × (4j + k) = 2i − j + 4k and |r × r| = √42 + 1 + 16 = √42 + 17. Thus
= 01 01 √42 + 17 = 01 √42 + 17 = 1 8 · 2 3(42 + 17)321 0
=
1
12(2132 − 1732) = 12 1 21√21 − 17√17 = 7 4√21 − 17 12√17
16. The sphere intersects the cone in the circle 2 + 2 = 1 2, = √12, so is the portion of the sphere where ≥ √12.
Using spherical coordinates to parametrize the sphere we have r( ) = sin cosi + sin sinj + cosk, and
|r × r| = sin (as in Example 1). The portion where ≥ √12 corresponds to 0 ≤ ≤ 4 , 0 ≤ ≤ 2 so
2 = 0204(sinsin)2(sin) = 02 sin2 04 sin3 = 02 sin2 04(1 − cos2 )sin
= 1 2 − 1 4 sin 22 0 1 3 cos3 − cos 0 4 = √122 − √22 − 1 3 + 1 = 2 3 − 512 √2
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.7 SURFACE INTEGRALS ¤ 687
17. Using spherical coordinates to parametrize the sphere we have r( ) = 2 sincosi + 2 sinsinj + 2 cos k and
|r × r| = 4 sin (see Example 16.6.10). Here is the portion of the sphere corresponding to 0 ≤ ≤ 2, so
(2 + 2) = (2 + 2) = 0202(4sin2 )(2cos)(4sin)
= 3202 02 sin3 cos = 32(2) 1 4 sin4 0 2 = 16(1 − 0) = 16
18. is given by r( ) = cos i + j + sin k, 0 ≤ ≤ 2, 0 ≤ ≤ . Then
r × r = j × (−sin i + cosk) = cos i + sin k and |r × r| = cos2 + sin2 = 1, so
( + + ) = 0 02(cos + + sin)(1) = 0 (cos + sin) + 1 22 =2 =0
= 0(2cos + 2sin + 2) = [2sin − 2cos + 2] 0 = 2 + 2 + 2 = 4 + 2
19. Here consists of three surfaces: 1, the lateral surface of the cylinder; 2, the front formed by the plane + = 5;
and the back, 3, in the plane = 0.
On 1: the surface is given by r( ) = i + 3cosj + 3sink, 0 ≤ ≤ 2, and 0 ≤ ≤ 5 − ⇒
0 ≤ ≤ 5 − 3cos. Then r × r = −3cos j − 3sin k and |r × r| = 9cos2 + 9sin2 = 3, so
1 = 0205 − 3 cos (3 sin)(3) = 902 1 22 =5 =0−3 cos sin
=
9 2
02 (5 − 3cos)2 sin = 9 2 1 9(5 − 3cos )32 0 = 0
On 2: r( ) = (5 − )i + j + k and |r × r| = |i + j| = √2, where 2 + 2 ≤ 9 and
2 =
2 + 2 ≤ 9
(5 − ) √2 = √20203 (5 − cos)( sin)
= √20203 (52 − 3 cos)(sin) = √202 5 33 − 1 44 cos =3 =0 sin
= √202 45 − 81 4 cos sin = √2 81 4 · 1 245 − 81 4 cos22 0 = 0
On 3: = 0 so 3 = 0. Hence = 0 + 0 + 0 = 0.
20. Let 1 be the lateral surface, 2 the top disk, and 3 the bottom disk.
On 1: r( ) = 3 cosi + 3 sinj + k, 0 ≤ ≤ 2, 0 ≤ ≤ 2, |r × r| = 3,
1(2 + 2 + 2) = 0202(9 + 2)3 = 2(54 + 8) = 124.
On 2: r( ) = cosi + sinj + 2k, 0 ≤ ≤ 3, 0 ≤ ≤ 2, |r × r| = ,
2(2 + 2 + 2) = 0203(2 + 4) = 2 81 4 + 18 = 153 2 .
On 3: r( ) = cosi + sinj, 0 ≤ ≤ 3, 0 ≤ ≤ 2, |r × r| = ,
3(2 + 2 + 2) = 0203(2 + 0) = 2 81 4 = 81 2 .
Hence 2 + 2 + 2 = 124 + 153 2 + 81 2 = 241.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.688 ¤ CHAPTER 16 VECTOR CALCULUS
21. From Exercise 5, r( ) = ( + )i + ( − )j + (1 + 2 + )k, 0 ≤ ≤ 2, 0 ≤ ≤ 1, and r × r = 3i + j − 2k.
Then
F(r( )) = (1 + 2 + )(+)(−) i − 3(1 + 2 + )(+)(−) j + ( + )( − )k
= (1 + 2 + )2−2 i − 3(1 + 2 + )2−2 j + (2 − 2)k
Because the -component of r × r is negative we use −(r × r) in Formula 9 for the upward orientation:
F · S = F · (−(r × r)) = 0102 −3(1 + 2 + )2−2 + 3(1 + 2 + )2−2 + 2(2 − 2)
= 0102 2(2 − 2) = 201 1 33 − 2 =2 =0 = 201 8 3 − 22
= 2 8 3 − 2 331 0 = 2 8 3 − 2 3 = 4
22. r( ) = hcos sin i, 0 ≤ ≤ 1, 0 ≤ ≤ and
r × r = hcos sin0i × h−sin cos1i = hsin −cos i. Here F(r( )) = i + sinj + cos k and,
by Formula 9,
F · S = F · (r × r) = 01 0( sin − sin cos + 2 cos)
= 01 sin − cos − 1 2sin2 + 2 sin = =0 = 01 = ]1 0 =
23. F( ) = i + j + k, = ( ) = 4 − 2 − 2, and is the square [01] × [01], so by Equation 10
F · S = [−(−2) − (−2) + ] = 01 01[22 + 22(4 − 2 − 2) + (4 − 2 − 2)]
= 01 22 + 8 33 − 2 323 − 2 55 + 4 − 3 − 1 33 =1 =0
= 01 1 32 + 11 3 − 3 + 34 15 = 1 93 + 11 6 2 − 1 44 + 34 151 0 = 713 180
24. F( ) = −i − j + 3 k, = ( ) = 2 + 2, and is the annular region ( ) | 1 ≤ 2 + 2 ≤ 9. Since
has downward orientation, we have
F · S = − −(−)2+ 2 − (−) 2+ 2 + 3
= − 2 2++2 2 + 2 + 2 3 = − 02 13 2 + 3
= − 02 13(2 + 4) = − 2 0 1 33 + 1 553 1
= −29 + 243 5 − 1 3 − 1 5 = − 1712 15
25. F( ) = i + j + 2 k, and using spherical coordinates, is given by = sincos , = sinsin, = cos ,
0 ≤ ≤ 2, 0 ≤ ≤ . F(r( )) = (sincos)i + (sinsin)j + (cos2 )k and, from Example 4,
r × r = sin2 cos i + sin2 sinj + sincosk. Thus
F(r( )) · (r × r) = sin3 cos2 + sin3 sin2 + sincos3 = sin3 + sincos3
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.7 SURFACE INTEGRALS ¤ 689
and
F · S = [F(r( )) · (r × r)] = 02 0(sin3 + sincos3 )
= 02 0(1 − cos2 + cos3 )sin = (2)−cos + 1 3 cos3 − 1 4 cos4 0
= 2 1 − 1 3 − 1 4 + 1 − 1 3 + 1 4 = 8 3
26. F( ) = i − j + 2 k, = ( ) = 4 − 2 − 2 and is the disk ( ) 2 + 2 ≤ 4. has downward
orientation, so by Equation 10,
F · S = − [− · 1 2(4 − 2 − 2)−12(−2) − (−) · 1 2(4 − 2 − 2)−12(−2) + 2]
= − 4 − 2 − 2 − 4 − 2 − 2 + 24 − 2 − 2
= − 24 − 2 − 2 = −202 02 √4 − 2 = −202 02 √4 − 2
= −2(2)− 1 2 · 2 3(4 − 2)322 0 = −4 0 + 1 3(4)32 = −4 · 8 3 = − 32 3
27. Let 1 be the paraboloid = 2 + 2, 0 ≤ ≤ 1 and 2 the disk 2 + 2 ≤ 1, = 1. Since is a closed
surface, we use the outward orientation.
On 1: F(r( )) = (2 + 2)j − k and r × r = 2i − j + 2 k (since the j-component must be negative on 1). Then
1 F · S =
2 + 2 ≤ 1
[−(2 + 2) − 22] = − 0201(2 + 22 sin2 )
= − 0201 3(1 + 2 sin2 ) = − 02(1 + 1 − cos 2) 01 3
= − 2 − 1 2 sin 22 0 1 441 0 = −4 · 1 4 = −
On 2: F(r( )) = j − k and r × r = j. Then 2 F · S =
2 + 2 ≤ 1
(1) = .
Hence F · S = − + = 0.
28. F( ) = i + j + k, = ( ) = sin, and is the rectangle [02] × [0 ], so by Equation 10
F · S = [−(sin) − (cos) + ] = 0 02(− sin2 − 3 sin cos + )
= 0 − 1 22 sin2 − 1 44 sin cos + 1 22 =2 =0
= 0 −2 sin2 − 4sin cos + 2 [integrate by parts in the first term]
= − 1 22 + 1 2 sin 2 + 1 4 cos 2 − 2sin2 + 2 0 = − 1 22 + 1 4 + 2 − 1 4 = 1 22
29. Here consists of the six faces of the cube as labeled in the figure. On 1:
F = i + 2j + 3 k, r × r = i and 1 F · S = −11 −11 = 4;
2: F = i + 2j + 3 k, r × r = j and 2 F · S = −11 −11 2 = 8;
3: F = i + 2 j + 3k, r × r = k and 3 F · S = −11 −11 3 = 12;
4: F = −i + 2 j + 3 k, r × r = −i and 4 F · S = 4;
5: F = i − 2j + 3 k, r × r = −j and 5 F · S = 8;
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.690 ¤ CHAPTER 16 VECTOR CALCULUS
6: F = i + 2 j − 3k, r × r = −k and 6 F · S = −11 −11 3 = 12.
Hence F · S =
6
=1
F · S = 48.
30. Here consists of three surfaces: 1, the lateral surface of the cylinder; 2, the front formed by the plane + = 2; and the
back, 3, in the plane = 0.
On 1: F(r( )) = sini + j + 5k and r × r = sini + cosk ⇒
1 F · S = 0202 − sin (sin2 + 5 cos)
= 02(2 sin2 + 10 cos − sin3 − 5sin cos ) = 2
On 2: F(r( )) = i + (2 − )j + 5k and r × r = i + j.
2 F · S =
2 + 2 ≤ 1
[ + (2 − )] = 2
On 3: F(r( )) = i + 5k and r × r = −j so 3 F · S = 0. Hence F · S = 4.
31. Here consists of four surfaces: 1, the top surface (a portion of the circular cylinder 2 + 2 = 1); 2, the bottom surface
(a portion of the -plane); 3, the front half-disk in the plane = 2, and 4, the back half-disk in the plane = 0.
On 1: The surface is = 1 − 2 for 0 ≤ ≤ 2, −1 ≤ ≤ 1 with upward orientation, so
1 F · S = 02 −11 −2 (0) − 2 −1− 2 + 2 = 02 −11 1−3 2 + 1 − 2
= 02 −1 − 2 + 1 3(1 − 2)32 + − 1 33 =1 =−1 = 02 4 3 = 8 3
On 2: The surface is = 0 with downward orientation, so
2 F · S =02 −11 −2 = 02 −11 (0) = 0
On 3: The surface is = 2 for −1 ≤ ≤ 1, 0 ≤ ≤ 1 − 2, oriented in the positive -direction. Regarding and as
parameters, we have r × r = i and
3 F · S =−11 0√1−2 2 = −11 0√1−2 4 = 4(3) = 2
On 4: The surface is = 0 for −1 ≤ ≤ 1, 0 ≤ ≤ 1 − 2, oriented in the negative -direction. Regarding and as
parameters, we use −(r × r) = −i and
4 F · S = −11 0√1−2 2 = −11 0√1−2 (0) = 0
Thus F · S = 8 3 + 0 + 2 + 0 = 2 + 8 3.
32. Here consists of four surfaces: 1, the triangular face with vertices (100), (010), and (0 0 1); 2, the face of the
tetrahedron in the -plane; 3, the face in the -plane; and 4, the face in the -plane.
On 1: The face is the portion of the plane = 1 − − for 0 ≤ ≤ 1, 0 ≤ ≤ 1 − with upward orientation, so
1 F · S = 01 01− [− (−1) − ( − )(−1) + ] = 01 01− ( + ) = 01 01− (1 − )
= 01 − 1 22 =1 =0− = 1 2 01 1 − 2 = 1 2 − 1 331 0 = 1 3
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.7 SURFACE INTEGRALS ¤ 691
On 2: The surface is = 0 with downward orientation, so
2 F · S =01 01− (−) = − 01 (1 − ) = − 1 22 − 1 331 0 = − 1 6
On 3: The surface is = 0 for 0 ≤ ≤ 1, 0 ≤ ≤ 1 − , oriented in the negative -direction. Regarding and as
parameters, we have r × r = −j and
3 F · S = 01 01− −( − ) = − 01 01− = − 01 1 22 =1 =0−
= −
1 2
01 (1 − )2 = 1 6 (1 − )31 0 = − 1 6
On 4: The surface is = 0 for 0 ≤ ≤ 1, 0 ≤ ≤ 1 − , oriented in the negative -direction. Regarding and as
parameters, we have r × r = i so we use −(r × r) = −i and
4 F · S = 01 01− (−) = − 01 (1 − ) = − 1 22 − 1 331 0 = − 1 6
Thus F · S = 1 3 − 1 6 − 1 6 − 1 6 = − 1 6.
33. = ⇒ = , = , so by Formula 4, a CAS gives
(2 + 2 + 2) = 0101(2 + 2 + 22)√2 + 22 + 1 ≈ 45822.
34. = 22 ⇒ = 22, = 22, so by Formula 4, a CAS gives
= 0201 (22)(22)2 + (22)2 + 1
= 0201 33424 + 442 + 1 = − 151 33 − 220 1 √3 + 1977 176 ln 7 − 9891 880 ln 3 + 440 3 √3tan−1 √53
35. We use Formula 4 with = 3 − 22 − 2 ⇒ = −4, = −2. The boundaries of the region
3 − 22 − 2 ≥ 0 are − 3 2 ≤ ≤ 3 2 and −√3 − 22 ≤ ≤ √3 − 22, so we use a CAS (with precision reduced to
seven or fewer digits; otherwise the calculation may take a long time) to calculate
222 = −√√3322 −√√33−−2222 22(3 − 22 − 2)2162 + 42 + 1 ≈ 34895
36. The flux of F across is given by F · S = F · n. Now on , = ( ) = 21 − 2, so = 0 and
= −2(1 − 2)−12. Therefore, by (10),
F · S = −22 −11 −2−2(1 − 2)−12 + 21 − 2 2 5 = 1 3(16 + 8025 − 80−25)
2 1 0
_1 0 1 2 0 _2
y
x
z
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.692 ¤ CHAPTER 16 VECTOR CALCULUS
37. If is given by = ( ), then is also the level surface ( ) = − ( ) = 0.
n =
∇( )
|∇( )| =
− i + j − k
√2 + 1 + 2 , and −n is the unit normal that points to the left. Now we proceed as in the
derivation of (10), using Formula 4 to evaluate
F · S = F · n = ( i + j + k)
i − j + k
2 + 1 + 2
2 + 1 + 2
where is the projection of onto the -plane. Therefore F · S = − + .
38. If is given by = ( ), then is also the level surface ( ) = − ( ) = 0.
n =
∇( )
|∇( )| =
i −
j − k
1 + 2 + 2 , and since the -component is positive this is the unit normal that points forward.
Now we proceed as in the derivation of (10), using Formula 4 for
F · S = F · n = ( i + j + k) 1 +i − j−2 + k 2 1 + 2 + 2
where is the projection of onto the -plane. Therefore F · S = − − .
39. = = · 4 1 22 = 22; by symmetry = = 0, and
= = 0202(cos)(2 sin) = 23− 1 4 cos 2 0 2 = 3.
Hence ( ) = 00 1 2.
40. is given by r( ) = i + j + 2 + 2 k, |r × r| = 1 + 2 2 + + 2 2 = √2 so
= 10 − 2 + 2 =
1 ≤ 2 + 2 ≤ 16
10 − 2 + 2 √2
= 0214 √2(10 − ) = 2 √252 − 1 334 1 = 108√2
41. (a) = (2 + 2)( )
(b) = (2 + 2)10 − 2 + 2 =
1 ≤ 2 + 2 ≤ 16
(2 + 2)10 − 2 + 2 √2
= 0214 √2(103 − 4) = 2√2 4329 10 = 4329 5 √2
42. Using spherical coordinates to parametrize the sphere we have r( ) = 5 sincosi + 5 sinsinj + 5 cos k, and
|r × r| = 25 sin (see Example 16.6.10). is the portion of the sphere where ≥ 4, so 0 ≤ ≤ tan−1(34) and
0 ≤ ≤ 2.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.7 SURFACE INTEGRALS ¤ 693
(a) = ( ) = 020tan−1(34) (25 sin) = 25 02 0tan−1(34) sin
= 25(2)−costan−1 3 4 + 1 = 50 − 4 5 + 1 = 10.
Because has constant density, = = 0 by symmetry, and
= 1
( ) = 101 020tan−1(34) (5 cos)(25 sin)
=
1
10 (125)02 0tan−1(34) sincos = 101 (125)(2) 1 2 sin2 tan 0 −1(34) = 25 · 1 2 3 5 2 = 9 2,
so the center of mass is ( ) = 00 9 2
(b) = (2 + 2)( ) = 020tan−1(34) (25 sin2 )(25 sin)
= 625 02 0tan−1(34) sin3 = 625(2) 1 3 cos3 − costan 0 −1(34)
= 1250 1 3 4 5 3 − 4 5 − 1 3 + 1 = 1250 375 14 = 140 3
43. The rate of flow through the cylinder is the flux v · n = v · S. We use the parametric representation
r( ) = 2cos i + 2sinj + k for , where 0 ≤ ≤ 2, 0 ≤ ≤ 1, so r = −2sini + 2cosj, r = k, and the
outward orientation is given by r × r = 2cosi + 2sinj. Then
v · S = 02 01 i + 4sin2 j + 4cos2 k · (2cosi + 2sinj)
= 02 01 2 cos + 8sin3 = 02 cos + 8sin3
= sin + 8− 1 3 (2 + sin2 )cos2 0 = 0 kgs
44. A parametric representation for the hemisphere is r( ) = 3sin cosi + 3sin sinj + 3cosk, 0 ≤ ≤ 2,
0 ≤ ≤ 2. Then r = 3cos cosi + 3cos sinj − 3sink, r = −3sinsini + 3sincosj, and the outward
orientation is given by r × r = 9sin2 cosi + 9sin2 sinj + 9sin cosk. The rate of flow through is
v · S = 02 02 (3sin sini + 3sin cosj) · 9sin2 cosi + 9sin2 sinj + 9sin cosk
= 27 02 02 sin3 sin cos + sin3 sin cos = 54 02 sin3 02 sin cos
= 54− 1 3(2 + sin2 )cos 0 2 1 2 sin2 2 0 = 0 kgs
45. consists of the hemisphere 1 given by = 2 − 2 − 2 and the disk 2 given by 0 ≤ 2 + 2 ≤ 2, = 0.
On 1: E = sin cosi + sin sinj + 2cosk,
T × T = 2 sin2 cos i + 2 sin2 sinj + 2 sin cosk. Thus
1 E · S = 0202(3 sin3 + 23 sin cos2 )
= 0202(3 sin + 3 sin cos2 ) = (2)31 + 1 3 = 8 33
On 2: E = i + j, and r × r = −k so 2 E · S = 0. Hence the total charge is = 0 E · S = 8 330.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.694 ¤ CHAPTER 16 VECTOR CALCULUS
46. Referring to the figure, on
1: E = i + j + k, r × r = i and 1 E · S = −11 −11 = 4;
2: E = i + j + k, r × r = j and 2 E · S = −11 −11 = 4;
3: E = i + j + k, r × r = k and 3 E · S = −11 −11 = 4;
4: E = −i + j + k, r × r = −i and 4 E · S = 4.
Similarly 5 E · S = 6 E · S = 4. Hence = 0 E · S = 0
6
= 1
E · S = 240.
47. ∇ = 65(4j + 4 k). is given by r( ) = i + √6 cosj + √6 sink and since we want the inward heat flow, we
use r × r = −√6 cosj − √6 sink. Then the rate of heat flow inward is given by
(− ∇) · S = 0204 −(65)(−24) = (2)(156)(4) = 1248.
48. ( ) = 2 + 2 + 2,
F = − ∇ = −−(2 + 2+ 2)32 i − (2 + 2+ 2)32 j − (2 + 2+ 2)32 k
=
(2 + 2 + 2)32 (i + j + k)
and the outward unit normal is n = 1
(i + j + k).
Thus F· n =
(2 + 2 + 2)32 (2 + 2 + 2), but on , 2 + 2 + 2 = 2 so F· n = 2 . Hence the rate of heat flow
across is F · S = 2 = 2 (42) = 4.
49. Let be a sphere of radius centered at the origin. Then |r| = and F(r) = r |r|3 = 3(i + j + k). A
parametric representation for is r( ) = sin cos i + sin sinj + cos k, 0 ≤ ≤ , 0 ≤ ≤ 2. Then
r = cos cosi+ cos sinj− sink, r = −sin sini+ sin cosj, and the outward orientation is given
by r × r = 2 sin2 cosi + 2 sin2 sinj + 2 sin cosk. The flux of F across is
F · S = 0 02
3 (sin cosi + sin sinj + cosk)
· 2 sin2 cosi + 2 sin2 sinj + 2 sin cosk
=
3
0 02 3 sin3 + sin cos2 = 0 02 sin = 4
Thus the flux does not depend on the radius .
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.8 STOKES’ THEOREM ¤ 695
16.8 Stokes' Theorem
1. Both and are oriented piecewise-smooth surfaces that are bounded by the simple, closed, smooth curve 2 + 2 = 4,
= 0 (which we can take to be oriented positively for both surfaces). Then and satisfy the hypotheses of Stokes’
Theorem, so by (3) we know curlF · S = F · r = curlF · S (where is the boundary curve).
2. The paraboloid = 1 − 2 − 2 intersects the -plane in the circle 2 + 2 = 1, = 0. This boundary curve should be
oriented in the counterclockwise direction when viewed from above, so a vector equation of is r() = cos i + sinj,
0 ≤ ≤ 2. Then r0() = −sini + cosj,
F(r()) = (cos)2(sin 0)i + (sin)2 j + (cos)(sin)k = sin2 j + sin cosk,
and by Stokes’ Theorem,
curlF · S = F · r = 02 F(r()) · r0() = 02(sin2 j + sin cosk) · (−sini + cosj)
= 02(0 + sin2 cos + 0) = 1 3 sin3 2 0 = 0
3. The boundary curve is the circle 2 + 2 = 16, = 0 where the hemisphere intersects the -plane. The curve should be
oriented in the counterclockwise direction when viewed from the right (from the positive -axis), so a vector equation of is
r() = 4 cos(−)i + 4 sin(−)k = 4 cosi − 4sink, 0 ≤ ≤ 2. Then r0() = −4sini − 4cosk and
F(r()) = (−4sin)0 i + (4 cos )(cos 0)j + (4 cos)(−4sin)(sin 0)k = −4sini + 4 cosj, and by Stokes’ Theorem,
curlF · S = F · r = 02 F(r()) · r0() = 02(−4sini + 4 cosj) · (−4sini − 4cosk)
= 02(16 sin2 + 0 + 0) = 16 1 2 − 1 4 sin 22 0 = 16
4. The boundary curve is the circle 2 + 2 = 4, = 2 which should be oriented in the counterclockwise direction when
viewed from the front, so a vector equation of is r() = 2i + 2 cosj + 2 sink, 0 ≤ ≤ 2. Then
F(r()) = tan−1(32 cossin2 )i + 8 cosj + 16 sin2 k, r0() = −2sinj + 2 cosk, and
F(r()) · r0() = −16 sincos + 32 sin2 cos. Thus
curlF · S = F · r = 02 F(r()) · r0() = 02(−16 sincos + 32 sin2 cos )
= −8sin2 + 32 3 sin3 2 0 = 0
5. is the square in the plane = −1. Rather than evaluating a line integral around we can use Equation 3:
1 curlF · S = F · r = 2 curlF · S where 1 is the original cube without the bottom and 2 is the bottom face
of the cube. curlF = 2 i + ( − 2)j + ( − )k. For 2, we choose n = k so that has the same orientation for
both surfaces. Then curlF· n = − = + on 2, where = −1. Thus 2 curlF· S = −11 −11( + ) = 0
so 1 curlF · S = 0.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.696 ¤ CHAPTER 16 VECTOR CALCULUS
6. The boundary curve is the circle 2 + 2 = 1, = 0 which should be oriented in the counterclockwise direction when
viewed from the right, so a vector equation of is r() = cos(−)i + sin(−)k = cos i − sink, 0 ≤ ≤ 2. Then
F(r()) = i + − cos sin j − cos2 sink, r0() = −sini − cosk, and F(r()) · r0() = −sin + cos3 sin. Thus
curlF · S = F · r = 02 F(r()) · r0() = 02(−sin + cos3 sin)
= cos − 1 4 cos4 2 0 = 0
7. curl F = −2 i − 2j − 2 k and we take the surface to be the planar region enclosed by , so is the portion of the plane
+ + = 1 over = {( ) | 0 ≤ ≤ 1, 0 ≤ ≤ 1 − }. Since is oriented counterclockwise, we orient upward.
Using Equation 16.7.10, we have = ( ) = 1 − − , = −2, = −2, = −2, and
F · r = curlF · S = [−(−2)(−1) − (−2)(−1) + (−2)]
= 01 01−(−2) = −201(1 − ) = −1
8. curlF = ( − )i − j + k and is the portion of the plane 3 + 2 + = 1 over
= ( ) | 0 ≤ ≤ 1 30 ≤ ≤ 1 2(1 − 3). We orient upward and use Equation 16.7.10 with
= ( ) = 1 − 3 − 2:
F · r = curlF · S = [−( − )(−3) − (−)(−2) + 1] = 013 0(1−3)2(1 + 3 − 5)
= 013 (1 + 3) − 5 22 =(1 =0 −3)2 = 013 1 2(1 + 3)(1 − 3) − 5 2 · 1 4(1 − 3)2
= 013 − 81 8 2 + 15 4 − 1 8 = − 27 8 3 + 15 8 2 − 1 81 03 = − 1 8 + 24 5 − 24 1 = 24 1
9. curlF = −i − j − k and we take to be the part of the paraboloid = 1 − 2 − 2 in the first octant. Since is
oriented counterclockwise (from above), we orient upward. Then using Equation 16.7.10 with = ( ) = 1 − 2 − 2
we have
F · r = curlF · S = [−(−)(−2) − (−)(−2) + (−)] = −2 − 2(1 − 2 − 2) −
= 02 01 −2( cos)( sin) − 2( sin)(1 − 2) − cos
= 02 01 −23 sin cos − 2(2 − 4)sin − 2 cos
= 02 − 1 24 sin cos − 2 1 33 − 1 55sin − 1 33 cos =1 =0
= 02 − 1 2 sin cos − 15 4 sin − 1 3 cos = − 1 4 sin2 + 15 4 cos − 1 3 sin 0 2
= −
1 4
−
4
15 −
1 3
= −
17
20
10. The curve of intersection is an ellipse in the plane = + 2. curlF = (1 − )i − j + ( − 2)k and we take the surface
to be the planar region enclosed by with upward orientation. From Equation 16.7.10 with = ( ) = + 2 we have
F · r = curlF · S =
2+2≤1
[−(1 − )(0) − (−1)(1) + ( + 2 − 2)]
=
2+2≤1
( + 1) = 02 01 ( sin + 1) = 02 1 33 sin + 1 22 =1 =0
= 02 1 3 sin + 1 2 = − 1 3 cos + 1 22 0 =
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.8 STOKES’ THEOREM ¤ 697
11. (a) The curve of intersection is an ellipse in the plane + + = 1 with unit normal n = √13 (i + j + k),
curlF = 2 j + 2 k, and curlF · n = √13(2 + 2). Then
F · r = √13 2 + 2 = 2 + 2 ≤ 9 2 + 2 = 0203 3 = 2 81 4 = 812
(b) (c) One possible parametrization is = 3 cos, = 3 sin,
= 1 − 3cos − 3sin, 0 ≤ ≤ 2.
12. (a) is the part of the surface = 2 − 2 that lies above the unit disk . curlF = i − j + (2 − 2)k = i − j.
Using Equation 16.7.10 with ( ) = 2 − 2, = , = −, we have
F · r = curlF · S = [−(−2) − (−)(2)] = 2(2 + 2)
= 20201 2 = 2(2) 1 441 0 =
(b) (c) One possible set of parametric equations is = cos,
= sin, = sin2 − cos2 , 0 ≤ ≤ 2.
13. The boundary curve is the circle 2 + 2 = 16, = 4 oriented in the clockwise direction as viewed from above (since is
oriented downward). We can parametrize by r() = 4 cosi − 4sinj + 4k, 0 ≤ ≤ 2, and then
r0() = −4sini − 4cosj. Thus F(r()) = 4 sini + 4 cosj − 2k, F(r()) · r0() = −16 sin2 − 16 cos2 = −16, and
F · r = 02 F(r()) · r0() = 02(−16) = −16 (2) = −32
Now curl F = 2k, and the projection of on the -plane is the disk 2 + 2 ≤ 16, so by Equation 16.7.10 with
= ( ) = 2 + 2 [and multiplying by −1 for the downward orientation] we have
curlF · S = − (−0 − 0 + 2) = −2 · () = −2 · (42 ) = −32
14. The paraboloid intersects the plane = 1 when 1 = 5 − 2 − 2 ⇔ 2 + 2 = 4, so the boundary curve is the circle
2 + 2 = 4, = 1 oriented in the counterclockwise direction as viewed from above. We can parametrize by
r() = 2 cosi + 2 sinj + k, 0 ≤ ≤ 2, and then r0() = −2sini + 2 cosj. Thus
F(r()) = −4sini + 2 sinj + 6 cosk, F(r()) · r0() = 8 sin2 + 4 sincos, and
F · r = 02(8 sin2 + 4 sincos) = 8 1 2 − 1 4 sin 2 + 2 sin2 2 0 = 8
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.698 ¤ CHAPTER 16 VECTOR CALCULUS
Now curl F = (−3 − 2)j+ 2 k, and the projection of on the -plane is the disk 2 + 2 ≤ 4, so by Equation 16.7.10
with = ( ) = 5 − 2 − 2 we have
curlF · S = [−0 − (−3 − 2)(−2) + 2] = [−6 − 42 + 2(5 − 2 − 2)]
= 02 02 −6 sin − 42 sin2 + 2(5 − 2) = 02 −23 sin − 4 sin2 + 52 − 1 2 4 =2 =0
= 02 −16 sin − 16 sin2 + 20 − 8 = 16 cos − 16 1 2 − 1 4 sin 2 + 122 0 = 8
15. The boundary curve is the circle 2 + 2 = 1, = 0 oriented in the counterclockwise direction as viewed from the positive
-axis. Then can be described by r() = cosi − sink, 0 ≤ ≤ 2, and r0() = −sini − cosk. Thus
F(r()) = −sinj + cos k, F(r()) · r0 () = −cos2 , and F · r = 02(−cos2 ) = − 1 2 − 1 4 sin 22 0 = −.
Now curlF = −i − j − k, and can be parametrized (see Example 16.6.10) by
r( ) = sin cosi + sin sinj + cosk, 0 ≤ ≤ , 0 ≤ ≤ . Then
r × r = sin2 cosi + sin2 sinj + sin cos k and
curlF · S =
2+2≤1
curlF · (r × r) = 0 0(−sin2 cos − sin2 sin − sin cos)
= 0(−2sin2 − sin cos) = 1 2 sin 2 − − 2 sin2 0 = −
16. Let be the surface in the plane + + = 1 with upward orientation enclosed by . Then an upward unit normal vector
for is n = √13 (i + j + k). Orient in the counterclockwise direction, as viewed from above. − 2 + 3 is
equivalent to F · r for F( ) = i − 2j + 3 k, and the components of F are polynomials, which have continuous
partial derivatives throughout R3. We have curl F = 3i + j − 2k, so by Stokes’ Theorem,
− 2 + 3 = F · r = curlF · n = (3i + j − 2k) · √13 (i + j + k)
=
2√
3 = √23 (surface area of )
Thus the value of − 2 + 3 is always √23 times the area of the region enclosed by , regardless of its shape or
location. [Notice that because n is normal to a plane, it is constant. But curl F is also constant, so the dot product curlF · nis
constant and we could have simply argued that curlF · n is a constant multple of , the surface area of .]
17. It is easier to use Stokes’ Theorem than to compute the work directly. Let be the planar region enclosed by the path of the
particle, so is the portion of the plane = 1 2 for 0 ≤ ≤ 1, 0 ≤ ≤ 2, with upward orientation.
curl F = 8i + 2 j + 2k and
F · r = curlF · S = −8 (0) − 2 1 2 + 2 = 01 02 2 − 1 2
= 01 02 3 2 = 01 3 42 =2 =0 = 01 3 = 3
18. ( + sin) + (2 + cos) + 3 = F · r, where F( ) = ( + sin)i + (2 + cos)j + 3 k ⇒
curlF = −2 i − 32 j − k. Since sin 2 = 2 sin cos , lies on the surface = 2. Let be the part of this surface that
is bounded by . Then the projection of onto the -plane is the unit disk [2 + 2 ≤ 1]. is traversed clockwise
(when viewed from above) so is oriented downward. Using Equation 16.7.10 with ( ) = 2,
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.9 THE DIVERGENCE THEOREM ¤ 699
= −2 = −2(2) = −4, = −32, = −1 and multiplying by −1 for the downward orientation, we have
F · r = − curlF · S = − −(−4)(2) − (−32)(2) − 1
= − (82 + 63 − 1) = − 0201(83 cos sin2 + 63 cos3 − 1)
= − 02 8 5 cos sin2 + 6 5 cos3 − 1 2 = − 15 8 sin3 + 6 5 sin − 1 3 sin3 − 1 2 2 0 =
19. Assume is centered at the origin with radius and let 1 and 2 be the upper and lower hemispheres, respectively, of .
Then curlF · S = 1 curlF · S + 2 curlF · S = 1F · r + 2F · r by Stokes’ Theorem. But 1 is the
circle 2 + 2 = 2 oriented in the counterclockwise direction while 2 is the same circle oriented in the clockwise direction.
Hence 2F · r = −1F · r so curlF · S = 0 as desired.
20. (a) By Exercise 16.5.26, curl(∇) = curl(∇) + ∇ × ∇ = ∇ × ∇ since curl(∇) = 0. Hence by Stokes’
Theorem (∇) · r = (∇ × ∇) · S.
(b) As in (a), curl(∇) = ∇ × ∇ = 0, so by Stokes’ Theorem, (∇) · r = [curl(∇)] · S = 0.
(c) As in part (a),
curl(∇ + ∇) = curl(∇) + curl(∇) [by Exercise 16.5.24]
= (∇ × ∇) + (∇ × ∇) = 0 [since u × v = −(v × u)]
Hence by Stokes’ Theorem, (∇ + ∇) · r = curl(∇ + ∇) · S = 0.
16.9 The Divergence Theorem
1. divF = 3 + + 2 = 3 + 3, so
divF = 010101(3 + 3) = 9 2 (notice the triple integral is
three times the volume of the cube plus three times ).
To compute F · S, on
1: n = i, F = 3i + j + 2 k, and 1 F · S = 1 3 = 3;
2: F = 3i + j + 2 k, n = j and 2 F · S = 2 = 1 2 ;
3: F = 3i + j + 2k, n = k and 3 F · S = 3 2 = 1;
4: F = 0, 4 F · S = 0; 5: F = 3i + 2k, n = −j and 5 F · S = 5 0 = 0;
6: F = 3i + j, n = −k and 6 F · S = 6 0 = 0. Thus F · S = 9 2 .
2. divF = 0 + 2 + 8 = 10 so, using cylindrical coordinates,
divF = 10 = 02 03 92 (10)
= 02 03 52 =9 =2 = 02 03(405 − 55)
= 02 03(405 − 55) = 2 0 405 2 2 − 5 663 0
= 2 3645 2 − 1215 2 = 2430
[continued]
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.700 ¤ CHAPTER 16 VECTOR CALCULUS
On 1: The surface is = 2 + 2, 2 + 2 ≤ 9, with downward orientation, and F( ) = 23 i + 2 j + 42 k.
Then
1 F · S = − [−(23)(2) − (2)(2) + (42)]
= 22(2 + 2)3 + 42(2 + 2) − 4(2 + 2)2
= 02 03 (23 cos sin2 · 6 + 42 sin2 · 2 − 44)
= 02 03 (210 sin2 cos + 45 sin2 − 45)
= 02 11 2 11 sin2 cos + 2 36 sin2 − 2 36 =3 =0
= 02 35411 ,294 sin2 cos + 486 sin2 − 486
= 35411 ,294 · 1 3 sin3 + 486 1 2 − 1 4 sin 2 − 4862 0
= 0 + 486( − 0) − 486(2) = −486
On 2: The surface is = 9, 2 + 2 ≤ 9, with upward orientation, so F( ) = 23 i + 2 j + 42 k and
2 F · S = [−(23)(0) − (2)(0) + (42)] = 4(9)2
= 324() = 324 · (3)2 = 2916
Thus F · S = 1 F · S + 2 F · S = −486 + 2916 = 2430.
3. divF = 0 + 1 + 0 = 1, so divF = 1 = () = 4 3 · 43 = 256 3 .
is a sphere of radius 4 centered at the origin which can be parametrized by r( ) = h4sincos4sinsin4cosi,
0 ≤ ≤ , 0 ≤ ≤ 2 (similar to Example 16.6.10). Then
r × r = h4coscos 4cos sin −4sini × h−4sinsin4sincos 0i
= 16 sin2 cos 16 sin2 sin16 cossin
and F(r( )) = h4cos4sinsin 4sincosi. Thus
F · (r × r) = 64 cossin2 cos + 64 sin3 sin2 + 64 cos sin2 cos = 128 cossin2 cos + 64 sin3 sin2
and
F · S = F · (r × r) = 02 0 (128 cossin2 cos + 64 sin3 sin2 )
= 02 128 3 sin3 cos + 64 1 3 cos3 − cossin2 = =0
= 02 256 3 sin2 = 256 3 1 2 − 1 4 sin 22 0 = 256 3
4. divF = 2 − 1 + 1 = 2, so
divF =
2+2≤9
02 2 =
2+2≤9
4 = 4(area of circle) = 4( · 32) = 36
Let 1 be the front of the cylinder (in the plane = 2), 2 the back (in the -plane), and 3 the lateral surface of the cylinder.
1 is the disk = 2, 2 + 2 ≤ 9. A unit normal vector is n = h100i and F = h4 − i on 1, so
1 F · S =1 F · n = 1 4 = 4(surface area of 1) = 4( · 32) = 36. 2 is the disk = 0, 2 + 2 ≤ 9.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.9 THE DIVERGENCE THEOREM ¤ 701
Here n =h−100i and F = h0 − i, so 2 F · S =2 F · n = 2 0 = 0.
3 can be parametrized by r( ) = h 3cos 3sini, 0 ≤ ≤ 2, 0 ≤ ≤ 2. Then
r × r = h100i × h0 −3sin3cosi = h0 −3cos −3sini. For the outward (positive) orientation we use
−(r × r) and F(r( )) = 2 −3cos 3sin, so
3 F · S = F · (−(r × r)) = 02 02 (0 − 9cos2 + 9sin2 )
= −902 02 cos2 = −9(2) 1 2 sin22 0 = 0
Thus F · S = 36 + 0 + 0 = 36.
5. divF =
() + (23) + (−) = + 23 − = 23, so by the Divergence Theorem,
F · S = divF = 03 02 01 23 = 203 02 01 3
= 2 1 223 0 1 222 0 1 441 0 = 2 9 2 (2) 1 4 = 9 2
6. divF =
(2) + (2) + (2) = 2 + 2 + 2 = 6, so by the Divergence Theorem,
F · S = divF = 0 0 0 6 = 60 0 0
= 6 1 22 0 1 22 0 1 22 0 = 6 1 22 1 22 1 22 = 3 4222
7. divF = 32 + 0 + 32, so using cylindrical coordinates with = cos, = sin, = we have
F · S = (32 + 32) = 02 01 −21(32 cos2 + 32 sin2 )
= 302 01 3 −21 = 3 2 0 1 441 0 2 −1 = 3(2) 1 4 (3) = 92
8. divF = 32 + 32 + 32, so by the Divergence Theorem,
F · S = 3(2 + 2 + 2) = 0 02 02 32 · 2 sin = 30 sin 02 02 4
= 3 [−cos] 0 2 0 1 552 0 = 3 (2) (2) 32 5 = 384 5
9. divF = + (−) + 0 = 0, so by the Divergence Theorem, F · S = 0 = 0.
10. The tetrahedron has vertices (0 0 0), (00), (0 0), (00 ) and is described by
= ( ) | 0 ≤ ≤ , 0 ≤ ≤ 1 − , 0 ≤ ≤ 1 − − . Here we have divF = 0 + 1 + = + 1, so
F · S = ( + 1) = 0 0(1− ) 0(1− − )( + 1)
= 0 0(1− ) ( + 1) 1 − − = 0 ( + 1) 1 − − 212 = =0(1− )
= 0 ( + 1)1 − · 1 − − 21 · 2 1 − 2 = 1 2 0 ( + 1) 1 − 2
=
1 2
0 12 3 + 12 2 − 2 2 + − 2 + 1
=
1 2
412 4 + 312 3 − 323 + 1 22 − 1 2 + 0
=
1 2
1 42 + 1 3 − 2 32 + 1 22 − + = 1 2 12 1 2 + 1 3 = 24 1 ( + 4)
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.702 ¤ CHAPTER 16 VECTOR CALCULUS
11. div F = 62 + 32 + 32 = 62 + 62 so
F · S = 6(2 + 2) = 02 01 01−2 62 · = 02 01 63(1 − 2)
= 02 01(63 − 65) = 2 0 3 24 − 61 0 = 2 3 2 − 1 =
12. For 2 + 2 ≤ 4 the plane = − 2 is below the -plane, so the solid bounded by is
= ( ) | 2 + 2 ≤ 4 − 2 ≤ ≤ 0. Here div F = + 2 + 2 − 2 = 3 so
F · S = 3 = 02 02 0sin −2 (3 sin)
= 02 02(32 sin)(0 − sin + 2) = 02 02 −33 sin2 + 62 sin
= 02 − 3 44 sin2 + 23 sin =2 =0 = 02 −12 sin2 + 16 sin
= −12 1 2 − 1 4 sin 2 − 16 cos2 0 = −12 − 16 + 16 = −12
13. F( ) = 2 + 2 + 2 i + 2 + 2 + 2 j + 2 + 2 + 2 k, so
divF = · 1
2(2 + 2 + 2)−12(2) + (2 + 2 + 2)12 + · 1 2(2 + 2 + 2)−12(2) + (2 + 2 + 2)12
+ · 1
2(2 + 2 + 2)−12(2) + (2 + 2 + 2)12
= (2 + 2 + 2)−12 2 + (2 + 2 + 2) + 2 + (2 + 2 + 2) + 2 + (2 + 2 + 2)
=
4(2 + 2 + 2)
2 + 2 + 2 = 42 + 2 + 2.
Then F · S = 42 + 2 + 2 = 020201 42 · 2 sin
= 02 sin 02 01 43 = [−cos] 0 2 []2 0 41 0 = (1) (2)(1) = 2
14. F( ) = (2 + 2 + 2)i + (2 + 2 + 2)j + (2 + 2 + 2)k, so
divF = · 2 + (2 + 2 + 2) + · 2 + (2 + 2 + 2) + · 2 + (2 + 2 + 2) = 5(2 + 2 + 2). Then
F · S = 5(2 + 2 + 2) = 0020 52 · 2 sin
= 50 sin 02 0 4 = 5 [−cos] 0 []2 0 1 55 0 = 5 (2) (2) 1 55 = 45
15. F · S = √3 − 2 = −11 −11 02 − 4 − 4 √3 − 2 = 341 60 √2 + 81 20 sin−1 √33
16.
By the Divergence Theorem, the flux of F across the surface of the cube is
F · S = 02 0202 cos cos2 + 3 sin2 cos cos4 + 5 sin4 cos cos6 = 19 642.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.SECTION 16.9 THE DIVERGENCE THEOREM ¤ 703
17. For 1 we have n = −k, so F · n = F · (−k) = −2 − 2 = −2 (since = 0 on 1). So if is the unit disk, we get
1 F · S = 1 F · n = (−2) = − 0201 2 (sin2 ) = − 1 4. Now since 2 is closed, we can use
the Divergence Theorem. Since divF = (2) + 1 33 + tan + (2 + 2) = 2 + 2 + 2, we use spherical
coordinates to get 2 F · S = divF = 020201 2 · 2 sin = 2 5. Finally
F · S = 2 F · S − 1 F · S = 2 5 − − 1 4 = 13 20.
18. As in the hint to Exercise 17, we create a closed surface 2 = ∪ 1, where is the part of the paraboloid 2 + 2 + = 2
that lies above the plane = 1, and 1 is the disk 2 + 2 = 1 on the plane = 1 oriented downward, and we then apply the
Divergence Theorem. Since the disk 1 is oriented downward, its unit normal vector is n = −k and F · (−k) = − = −1 on
1. So 1 F · S = 1 F · n = 1(−1) = −(1) = −. Let be the region bounded by 2. Then
2 F · S = divF = 1 = 010212−2 = 0102( − 3) = (2) 1 4 = 2 . Thus the
flux of F across is F · S = 2 F · S − 1 F · S = 2 − (−) = 32 .
19. The vectors that end near 1 are longer than the vectors that start near 1, so the net flow is inward near 1 and divF(1) is
negative. The vectors that end near 2 are shorter than the vectors that start near 2, so the net flow is outward near 2 and
divF(2) is positive.
20. (a) The vectors that end near 1 are shorter than the vectors that start near 1, so the net flow is outward and 1 is a source.
The vectors that end near 2 are longer than the vectors that start near 2, so the net flow is inward and 2 is a sink.
(b) F( ) = 2 ⇒ divF = ∇ · F = 1 + 2. The -value at 1 is positive, so divF = 1 + 2 is positive, thus 1
is a source. At 2, −1, so divF = 1 + 2 is negative, and 2 is a sink.
21. From the graph it appears that for points above the -axis, vectors starting near a
particular point are longer than vectors ending there, so divergence is positive.
The opposite is true at points below the -axis, where divergence is negative.
F( ) = + 2 ⇒ divF = () + + 2 = + 2 = 3.
Thus divF 0 for 0, and divF 0 for 0.
22. From the graph it appears that for points above the line = −, vectors starting
near a particular point are longer than vectors ending there, so divergence is
positive. The opposite is true at points below the line = −, where divergence
is negative.
F( ) = 2 2 ⇒ divF = (2) + (2) = 2 + 2. Then
div F 0 for 2 + 2 0 ⇒ −, and divF 0 for −.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.704 ¤ CHAPTER 16 VECTOR CALCULUS
23. Since x
|x|3 =
i + j + k
(2 + 2 + 2)32 and (2 + 2+ 2)32 = ((2+2 +2+2 +2)2−)5322 with similar expressions
for
(2 + 2+ 2)32 and (2 + 2+ 2)32 , we have
div|xx|3 = 3(2 + (2+2 +2)2−+3( 22 )5+22 + 2) = 0, except at (000) where it is undefined.
24. We first need to find F so that F · n = (2 + 2 + 2), so F · n = 2 + 2 + 2. But for ,
n =
i + j + k
2 + 2 + 2 = i + j + k. Thus F = 2i + 2j + k and divF = 1.
If = ( ) | 2 + 2 + 2 ≤ 1, then (2 + 2 + 2) = = () = 4 3(1)3 = 4 3.
25. a · n = diva = 0 since diva = 0.
26. 1
3 F · S = 1 3 divF = 1 3 3 = ()
27. curlF · S = div(curlF) = 0 by Theorem 16.5.11.
28. n = (∇ · n) = div(∇) = ∇2
29. (∇) · n = div(∇) = (∇2 + ∇ · ∇) by Exercise 16.5.25.
30. (∇ − ∇) · n = (∇2 + ∇ · ∇) − (∇2 + ∇ · ∇) [by Exercise 29].
But ∇ · ∇ = ∇ · ∇, so that (∇ − ∇) · n = (∇2 − ∇2) .
31. If c = 1 i + 2 j + 3 k is an arbitrary constant vector, we define F = c = 1 i + 2 j + 3 k. Then
divF = div c =
1 +
2 +
3 = ∇ · c and the Divergence Theorem says F · S = divF ⇒
F · n = ∇ · c . In particular, if c = i then i · n = ∇ · i ⇒
1 = (where n = 1 i + 2 j + 3 k). Similarly, if c = j we have 2 = ,
and c = k gives 3 = . Then
n = 1 i + 2 j + 3 k
= i + j + k = i + j + k
= ∇ as desired.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.CHAPTER 16 REVIEW ¤ 705
32. By Exercise 31, n = ∇ , so
F = − n = − ∇ = − ∇() = − ( k) = − k = − ()k.
But the weight of the displaced liquid is volume × density × = (), thus F = −k as desired.
16 Review
1. False; divF is a scalar field.
2. True. (See Definition 16.5.1.)
3. True, by Theorem 16.5.3 and the fact that div0 = 0.
4. True, by Theorem 16.3.2.
5. False. See Exercise 16.3.35. (But the assertion is true if is simply-connected; see Theorem 16.3.6.)
6. False. See the discussion accompanying Figure 8 on page 1120 [ET 1080].
7. False. For example, div( i) = 0 = div(j) but i 6= j.
8. True. Line integrals of conservative vector fields are independent of path, and by Theorem 16.3.3, work = F · r = 0 for
any closed path .
9. True. See Exercise 16.5.24.
10. False. F · G is a scalar field, so curl(F · G) has no meaning.
11. True. Apply the Divergence Theorem and use the fact that divF = 0.
12. False by Theorem 16.5.11, because if it were true, then div curlF = 3 6= 0.
13. False. By Equations 16.4.5, the area is given by − or .
1. (a) Vectors starting on point in roughly the direction opposite to , so the tangential component F · T is negative.
Thus F · r = F · T is negative.
(b) The vectors that end near are shorter than the vectors that start near , so the net flow is outward near and
divF() is positive.
2. We can parametrize by = , = 2, 0 ≤ ≤ 1 so
= 01 1 + (2)2 = 12 1 (1 + 42)321 0 = 12 1 5√5 − 1.
3. cos = 0 (3cos )(3sin)cos (1)2 + (−3sin)2 + (3cos )2 = 0(9cos2 sin)√10
= 9√10− 1 3 cos3 0 = −3√10(−2) = 6√10
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.706 ¤ CHAPTER 16 VECTOR CALCULUS
4. = 3cos ⇒ = −3sin , = 2 sin ⇒ = 2 cos , 0 ≤ ≤ 2, so
+ + 2 = 02 (2sin)(−3sin) + (3cos + 4sin2 )(2cos)
= 02(−6sin2 + 6cos2 + 8sin2 cos) = 02 6(cos2 − sin2 ) + 8sin2 cos
= 02(6cos2 + 8sin2 cos ) = 3sin2 + 8 3 sin3 2 0 = 0
Or: Notice that
() = 1 = + 2, so F( ) = + 2 is a conservative vector field. Since is a closed
curve, F · r = + ( + 2) = 0.
5. 3 + 2 = −11 3(−2) + (1 − 2)2 = −11(−4 − 22 + 1)
= − 1 55 − 2 33 + 1 −1 = − 1 5 − 2 3 + 1 − 1 5 − 2 3 + 1 = 15 4
6. + + = 01 √4 · 2 · 43 + 2 · 2 + 4 · 3 · 32 = 01(46 + 22 + 39)
= 4 77 + 2 + 10 3 101 0 = − 70 9
7. : = 1 + 2 ⇒ = 2, = 4 ⇒ = 4, = −1 + 3 ⇒ = 3, 0 ≤ ≤ 1.
+ 2 + = 01[(1 + 2)(4)(2) + (4)2(4) + (4)(−1 + 3)(3)]
= 01(1162 − 4) = 116 3 3 − 221 0 = 116 3 − 2 = 110 3
8. F(r()) = (sin)(1 + )i + (sin2 )j, r0() = cosi + j and
F · r = 0((1 + )sincos + sin2 ) = 0 1 2(1 + )sin2 + sin2
= 1 2 (1 + )− 1 2 cos 2 + 1 4 sin 2 + 1 2 − 1 4 sin 2 0 = 4
9. F(r()) = − i + 2(−)j + (2 + 3)k, r0() = 2i + 32 j − k and
F · r = 01(2− − 35 − (2 + 3)) = −2− − 2− − 1 26 − 1 33 − 1 441 0 = 11 12 − 4.
10. (a) : = 3 − 3, = 2 , = 3, 0 ≤ ≤ 1. Then
= F · r = 01 3i + (3 − 3)j + 2 k · −3i + 2 j + 3k = 01 −9 + 32 = 1 2(3 − 9).
(b) = F · r = 02(3 sini + 3 cosj + k) · (−3sini + j + 3 cosk)
= 02(−9sin2 + 3 cos + 3 cos) = −9 1 2 − 1 4 sin 2 + 3 sin + 3(sin + cos) 0 2
= −
9
4 + 3 + 32 − 3 = − 34
11.
[(1 + )] = 2 + 2 = + 2 and the domain of F is R2, so F is conservative. Thus there
exists a function such that F = ∇. Then ( ) = + 2 implies ( ) = + + () and then
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.CHAPTER 16 REVIEW ¤ 707
( ) = + + 0() = (1 + ) + 0(). But ( ) = (1 + ), so 0() = 0 ⇒ () = .
Thus ( ) = + + is a potential function for F.
12. F is defined on all of R3, its components have continuous partial derivatives, and
curl F = (0 − 0)i − (0 − 0)j + (cos − cos)k = 0, so F is conservative by Theorem 16.5.4. Thus there exists a function
such that ∇ = F. Then ( ) = sin implies ( ) = sin + ( ) and then
( ) = cos + ( ). But ( ) = cos, so ( ) = 0 ⇒ ( ) = (). Then
( ) = sin + () implies ( ) = 0(). But ( ) = −sin, so () = cos + . Thus a potential
function for F is ( ) = sin + cos + .
13. Since
(432 − 23) = 83 − 62 = (24 − 322 + 43) and the domain of F is R2, F is conservative.
Furthermore ( ) = 42 − 23 + 4 is a potential function for F. = 0 corresponds to the point (01) and = 1
corresponds to (11), so F · r = (11) − (01) = 1 − 1 = 0.
14. Here curl F = 0, the domain of F is R3, and the components of F have continuous partial derivatives, so F is conservative.
Furthermore ( ) = + is a potential function for F. Then F · r = (403) − (020) = 4 − 2 = 2.
15. 1: r() = i + 2 j, −1 ≤ ≤ 1;
2: r() = −i + j, −1 ≤ ≤ 1.
Then
2 − 2 = −11(5 − 25) + −11
= − 1 6 61 −1 + 1 2 21 −1 = 0
Using Green’s Theorem, we have
2 − 2 = (−2) − (2) = (−2 − 2) = −11 12 −4
= −11 −22 =1 =2 = −11 (25 − 2) = 1 3 6 − 21 −1 = 0
16. √1 + 3 + 2 = (2) − √1 + 3 = 01 03(2 − 0) = 01 92 = 331 0 = 3
17. 2 − 2 =
2 + 2 ≤ 4
(−2) − (2) =
2 + 2 ≤ 4
(−2 − 2) = − 0202 3 = −8
18. curlF = (0 − − cos)i − (− cos − 0)j + (0 − − cos )k = −− cos i − − cosj − − cosk,
divF = −− sin − − sin − − sin
19. If we assume there is such a vector field G, then div(curlG) = 2 + 3 − 2. But div(curlF) = 0 for all vector fields F.
Thus such a G cannot exist.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.708 ¤ CHAPTER 16 VECTOR CALCULUS
20. Let F = 1 i + 1 j + 1 k and G = 2 i + 2 j + 2 k be vector fields whose first partials exist and are continuous. Then
FdivG − GdivF = 1 2 + 2 + 2 i + 1 2 + 2 + 2 j + 1 2 + 2 + 2 k
− 2 1 + 1 + 1 i + 2 1 + 1 + 1 j
+2 1 + + 1 k
and
(G · ∇)F − (F · ∇)G = 2 1 + 2 1 + 2 1 i + 2 1 + 2 1 + 2 1 j
+2 1 + 2 1 + 2 1 k
− 1 2 + 1 2 + 1 2 i + 1 2 + 1 2 + 1 2 j
+1 2 + 1 2 + 1 2 k
Hence
FdivG − GdivF + (G · ∇)F − (F · ∇)G
= 1 2 + 2 1 − 2 1 + 1 2
− 2 1 + 1 2 + 1 2 + 2 1 i
+1 2 + 2 1 − 2 1 + 1 2
− 1 2 + 2 1 + 2 1 + 1 2 j
+2 1 + 1 2 − 1 2 + 2 1
− 1 2 + 2 1 + 2 1 + 1 2 k
= (12 − 21) − (21 − 12)i
+ (12 − 21) − (12 − 21)j
+ (21 − 12) − (12 − 21)k
= curl (F × G)
21. For any piecewise-smooth simple closed plane curve bounding a region , we can apply Green’s Theorem to
F( ) = ()i + ()j to get () + () = () − () = 0 = 0.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.CHAPTER 16 REVIEW ¤ 709
22. ∇2() = 2()
2 +
2()
2 +
2()
2
=
+ + + + + [Product Rule]
=
2
2 + 2 + 22 + 22 + 2
+ 2
2 +
2
2 + 2 + 22 [Product Rule]
= 22 + 22 + 22 + 22 + 22 + 22 + 2 ·
= ∇2 + ∇2 + 2∇ · ∇
Another method: Using the rules in Exercises 14.6.37(b) and 16.5.25, we have
∇2() = ∇ · ∇() = ∇ · ( ∇ + ∇) = ∇ · ∇ + ∇ · ∇ + ∇ · ∇ + ∇ · ∇
= ∇2 + ∇2 + 2∇ · ∇
23. ∇2 = 0 means that 2
2 +
2
2 = 0. Now if F = i − j and is any closed path in , then applying Green’s
Theorem, we get
F · r = − = (−) − ()
= − ( + ) = − 0 = 0
Therefore the line integral is independent of path, by Theorem 16.3.3.
24. (a) 2 + 2 = cos2 + sin2 = 1, so lies on the circular cylinder 2 + 2 = 1.
But also = , so lies on the plane = . Thus is contained in the
intersection of the plane = and the cylinder 2 + 2 = 1; with 0 ≤ ≤ 2 we
get the entire intersection (an ellipse).
(b) Apply Stokes’ Theorem, F · r = curlF · S:
curlF =
i j k
22 222 + 2 cot −2 csc2
= −2 csc2 − (−2 csc2 )042 − 42 = 0
Therefore F · r = 0 · S = 0.
25. = ( ) = 2 + 2 with 0 ≤ ≤ 1, 0 ≤ ≤ 2. Thus
() = √1 + 42 + 4 = 0102 √5 + 42 = 01 2 √5 + 42 = 1 6(5 + 42)321 0 = 1 627 − 5√5.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.710 ¤ CHAPTER 16 VECTOR CALCULUS
26. (a) r = − j + 2k, r = 2 i − j and
r × r = 22 i + 4j + 22 k. Since the point (4 −2 1)
corresponds to = 1, = 2 (or = −1, = −2 but r × r
is the same for both), a normal vector to the surface at (4 −21)
is 2i + 8j + 8k and an equation of the tangent plane is
2 + 8 + 8 = 0 or + 4 + 4 = 0.
(b)
(c) By Definition 16.6.6, the area of is given by
() = |r × r | = 03−33 (22)2 + (4)2 + (22)2 = 203−33 √4 + 422 + 4 .
(d) By Equation 16.7.9, the surface integral is
F · S = F · (r × r ) = 03−33 1 + ( (2)22)2 1 + ( (−2) 2 )2 1 + ( (− 2)2)2 · 22422
= 03−33 1 + 264 + 1 +4 252 + 1 + 2244 ≈ 15240190
27. = ( ) = 2 + 2 with 0 ≤ 2 + 2 ≤ 4 so r × r = −2i − 2 j + k. Then
=
2 + 2 ≤ 4
(2 + 2)42 + 42 + 1
= 0202 3√1 + 42 = 60 1 391√17 + 1
(Substitute = 1 + 42 and use tables.)
28. = ( ) = 4 + + with 0 ≤ 2 + 2 ≤ 4 so r × r = −i − j + k. Then
(2 + 2) =
2 + 2 ≤ 4
(2 + 2)(4 + + )√3
= 0202 √33(4 + cos + sin) = 02 8 √33 = 32 √3
29. Since the sphere bounds a simple solid region, the Divergence Theorem applies and
F · S = divF = ( − 2) = − 2
= 0 and odd function in is symmetric − 2 · () = −2 · 4 3 (2)3 = − 64 3
Alternate solution: F(r( )) = 4sin cos cosi − 4sin sinj + 6sin cosk,
r × r = 4sin2 cosi + 4sin2 sinj + 4sin cos k, and
F · (r × r) = 16sin3 cos2 cos − 16sin3 sin2 + 24sin2 cos cos . Then
F · S = 020(16sin3 cos cos2 − 16sin3 sin2 + 24sin2 cos cos)
= 02 4 3(−16sin2 ) = − 64 3
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.CHAPTER 16 REVIEW ¤ 711
30. = ( ) = 2 + 2, r × r = −2i − 2 j + k (because of upward orientation) and
F(r( )) · (r × r) = −23 − 22 + 2 + 2. Then
F · S =
2 + 2 ≤ 1
(−23 − 22 + 2 + 2)
= 0102(−23 cos3 − 23 cos sin2 + 2) = 01 3(2) = 2
31. Since curlF = 0, (curlF) · S = 0. We parametrize : r() = cosi + sinj, 0 ≤ ≤ 2 and
F · r = 02(−cos2 sin + sin2 cos) = 1 3 cos3 + 1 3 sin3 2 0 = 0.
32. curlF · S = F · r where : r() = 2 cosi + 2 sinj + k, 0 ≤ ≤ 2, so r0() = −2sini + 2 cosj,
F(r()) = 8 cos2 sini + 2 sinj + 4 cos sin k, and F(r()) · r0() = −16 cos2 sin2 + 4 sincos. Thus
F · r = 02(−16 cos2 sin2 + 4 sin cos) = −16− 1 4 sin cos3 + 16 1 sin 2 + 1 8 + 2 sin2 2 0 = −4.
33. The surface is given by + + = 1 or = 1 − − , 0 ≤ ≤ 1, 0 ≤ ≤ 1 − and r × r = i + j + k. Then
F · r = curlF · S = (− i − j − k) · (i + j + k) = (−1) = −(area of ) = − 1 2 .
34. F · S = 3(2 + 2 + 2) = 020102(32 + 32) = 2 01(63 + 8) = 11
35. divF =
2 + 2 + 2 ≤ 1
3 = 3(volume of sphere) = 4. Then
F(r( )) · (r × r) = sin3 cos2 + sin3 sin2 + sin cos2 = sin and
F · S = 020 sin = (2)(2) = 4.
36. Here we must use Equation 16.9.7 since F is not defined at the origin. Let 1 be the sphere of radius 1 with center at the origin
and outer unit normal n1. Let 2 be the surface of the ellipsoid with outer unit normal n2 and let be the solid region
between 1 and 2. Then the outward flux of F through the ellipsoid is given by
2 F · n2 = − 1 F · (−n1) + divF . But F = r |r|3, so
divF = ∇ · |r|−3 r = |r|−3(∇ · r) + r · ∇ |r|−3 = |r|−3 (3) + r · −3|r|−4r|r|−1 = 0. [Here we have
used Exercises 16.5.30(a) and 16.5.31(a).] And F · n1 = r
|r|3 ·
r
|r| = |r|−2 = 1 on 1.
Thus 2 F · n2 = 1 + 0 = (surface area of the unit sphere) = 4(1)2 = 4.
37. Because curlF = 0, F is conservative, so there exists a function such that ∇ = F. Then ( ) = 32 − 3
implies ( ) = 3 − 3 + ( ) ⇒ ( ) = 3 − 3 + ( ). But ( ) = 3 − 3, so
( ) = () and ( ) = 3 − 3 + (). Then ( ) = 3 + 0() but ( ) = 3 + 2,
so () = 2 + and a potential function for F is ( ) = 3 − 3 + 2. Hence
F · r = ∇ · r = (030) − (0 0 2) = 0 − 4 = −4.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.712 ¤ CHAPTER 16 VECTOR CALCULUS
38. Let 0 be the circle with center at the origin and radius as in the figure.
Let be the region bounded by and 0. Then ’s positively oriented
boundary is ∪ (−0). Hence by Green’s Theorem
F · r + −0 F · r = − = 0, so
F · r = − −0 F · r = 0 F · = 02 F(r()) · r0()
= 0223 cos3 + 23 cos 2 sin2 − 2sin (−sin) + 23 sin3 + 23 cos 22 sin + 2cos (cos )
= 02 222 = 4
39. By the Divergence Theorem, F · n = divF = 3(volume of ) = 3(8 − 1) = 21.
40. The stated conditions allow us to use the Divergence Theorem. Hence curlF · S = div(curlF) = 0
since div(curlF) = 0.
41. Let F = a × r = h1 2 3i × h i = h2 − 3 3 − 1 1 − 2i. Then curl F = h21 2223i = 2a,
and 2a · S = curlF · S = F · r = (a × r) · r by Stokes’ Theorem.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.PROBLEMS PLUS
1. Let 1 be the portion of Ω() between () and , and let 1 be its boundary. Also let be the lateral surface of 1 [that
is, the surface of 1 except and ()]. Applying the Divergence Theorem we have 1 r·3n = 1 ∇ · r3 .
But
∇ · r
3 = · (2 + 2+ 2)32 (2 + 2+ 2)32 (2 + 2+ 2)32
=
(2 + 2 + 2 − 32) + (2 + 2 + 2 − 32) + (2 + 2 + 2 − 32)
(2 + 2 + 2)52 = 0
⇒ 1 r·3n = 1 0 = 0. On the other hand, notice that for the surfaces of 1 other than () and ,
r · n = 0 ⇒
0 = 1 r·3n = r·3n + () r·3n + r·3n = r·3n + () r·3n ⇒
r·3n = − () r·3n . Notice that on (), = ⇒ n = −r = −r and r · r = 2 = 2, so
that −() r·3n = () r·4r = () 2 4 = 12 () = area of 2 () = |Ω()|.
Therefore |Ω()| = r·3n .
2. By Green’s Theorem
(3 − ) − 23 = (− 23) − ( 3 − ) = (1 − 62 − 32)
Notice that for 62 + 32 1, the integrand is negative. The integral has maximum value if it is evaluated only in the region
where the integrand is positive, which is within the ellipse 62 + 32 = 1. So the simple closed curve that gives a maximum
value for the line integral is the ellipse 62 + 32 = 1.
3. The given line integral 1 2 ( − ) + ( − ) + ( − ) can be expressed as F· r if we define the vector
field F by F( ) = i + j + k = 1 2( − )i + 1 2( − )j + 1 2( − )k. Then define to be the planar
interior of , so is an oriented, smooth surface. Stokes’ Theorem says F · r = curlF · S = curlF · n.
Now
curlF = − i + − j + − k
= 1 2 + 1 2i + 1 2 + 1 2j + 1 2 + 1 2k = i + j + k = n
so curlF · n = n · n = |n|2 = 1, hence curlF · n = which is simply the surface area of Thus,
F · r = 1
2 ( − ) + ( − ) + ( − ) is the plane area enclosed by .
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. 713
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.714 ¤ CHAPTER 16 PROBLEMS PLUS
4. The surface given by = sin, = sin, = sin( + ) is difficult to visualize, so we first graph the surface from three
different points of view.
The trace in the horizontal plane = 0 is given by = sin( + ) = 0 ⇒ + = [ an integer]. Then
we can write = − , and the trace is given by the parametric equations = sin,
= sin = sin( − ) = sin cos − cos sin = ±sin, and since sin = , the trace consists of the two lines
= ±.
If = 1, = sin( + ) = 1 ⇒ + = 2 + 2. So = 2 + 2 − and the trace in = 1 is given by the
parametric equations = sin, = sin = sin 2 + 2 − = sin 2 + 2cos − cos 2 + 2sin = cos.
This curve is equivalent to 2 + 2 = 1, = 1, a circle of radius 1. Similarly, in = −1 we have = sin( + ) = −1 ⇒
+ = 3
2 + 2 ⇒ = 32 + 2 − , so the trace is given by the parametric equations = sin,
= sin = sin 32 + 2 − = sin 32 + 2cos − cos 32 + 2sin = −cos, which again is a circle,
2 + 2 = 1, = −1.
If = 1
2, = sin( + ) = 1 2 ⇒ + = + 2 where = 6 or 56 . Then = ( + 2) − and the trace in
= 1
2 is given by the parametric equations = sin,
= sin = sin[( + 2) − ] = sin( + 2) cos − cos( + 2) sin = 1 2 cos ± √23 sin. In rectangular
coordinates, = sin so = 1 2 cos ± √23 ⇒ ± √23 = 1 2 cos ⇒ 2 ± √3 = cos But then
2 + 2 ± √32 = sin2 + cos2 = 1 ⇒ 2 + 42 ± 4√3 + 32 = 1 ⇒ 42 ± 4√3 + 42 = 1, which
may be recognized as a conic section. In particular, each equation is an ellipse rotated ±45◦ from the standard orientation (see
the following graph). The trace in = − 1 2 is similar: = sin( + ) = − 1 2 ⇒ + = + 2 where = 76 or 116 .
Then = ( + 2) − and the trace is given by the parametric equations = sin,
= sin = sin[( + 2) − ] = sin( + 2) cos − cos( + 2) sin = − 1 2 cos ± √23 sin. If we convert to
rectangular coordinates, we arrive at the same pair of equations, 42 ± 4√3 + 42 = 1, so the trace is identical to the trace
in = 1
2.
Graphing each of these, we have the following 5 traces.
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.CHAPTER 16 PROBLEMS PLUS ¤ 715
= −1 = − 1
2 = 0
= 1
2 = 1
Visualizing these traces on the surface reveals that horizontal cross sections are pairs of intersecting ellipses whose major axes
are perpendicular to each other. At the bottom of the surface, = −1, the ellipses coincide as circles of radius 1. As we move
up the surface, the ellipses become narrower until at = 0 they collapse into line segments, after which the process is
reversed, and the ellipses widen to again coincide as circles at = 1.
5. (F · ∇)G = 1 + 1 + 1 (2 i + 2 j+2 k)
= 1 2 + 1 2 + 1 2 i + 1 2 + 1 2 + 1 2 j
+ 1 2 + 1 2 + 1 2 k
= (F · ∇2)i +(F · ∇2)j + (F · ∇2)k.
Similarly, (G · ∇)F = (G · ∇1)i +(G · ∇1)j +(G · ∇1)k. Then
F × curlG =
i 1
2 − 2
j
1
2 − 2
k 1
2 − 2
= 1 2 − 1 2 − 1 2 + 1 2 i + 1 2 − 1 2 − 1 2 + 1 2 j
+1 2 − 1 2 − 1 2 + 1 2 k
[continued]
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.716 ¤ CHAPTER 16 PROBLEMS PLUS
and
G × curlF = 2 1 − 2 1 − 2 1 + 2 1 i + 2 1 − 2 1 − 2 1 + 2 1 j
+2 1 − 2 1 − 2 1 + 2 1 k.
Then
(F · ∇)G + F × curlG = 1 2 + 1 2 + 1 2 i +1 2 + 1 2 + 1 2 j
+1 2 + 1 2 + 1 2 k
and
(G · ∇)F + G × curlF = 2 1 + 2 1 + 2 1 i +2 1 + 2 1 + 2 1 j
+2 1 + 2 1 + 2 1 k.
Hence
(F · ∇)G + F × curlG +(G · ∇)F + G × curlF
= 1 2 + 2 1 + 1 2 + 2 1 + 1 2 + 2 1 i
+1 2 + 2 1 + 1 2 + 2 1 + 1 2 + 2 1 j
+1 2 + 2 1 + 1 2 + 2 1 + 1 2 + 2 1 k
= ∇(12 + 12 + 12) = ∇(F · G).
6. (a) First we place the piston on coordinate axes so the top of the cylinder is at the origin and () ≥ 0 is the distance from the
top of the cylinder to the piston at time . Let 1 be the curve traced out by the piston during one four-stroke cycle, so 1
is given by r() = ()i, ≤ ≤ . (Thus, the curve lies on the positive -axis and reverses direction several times.) The
force on the piston is ()i, where is the area of the top of the piston and () is the pressure in the cylinder at time .
As in Section 16.2, the work done on the piston is 1 F · r = ()i · 0()i = ()0() . Here, the
volume of the cylinder at time is () = () ⇒ 0() = 0() ⇒ ()0() = () 0() .
Since the curve in the -plane corresponds to the values of and at time , ≤ ≤ , we have
= ()0() = () 0() =
Another method: If we divide the time interval [ ] into subintervals of equal length ∆, the amount of work done on
the piston in the th time interval is approximately ()[() − (−1)]. Thus we estimate the total work done during
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.CHAPTER 16 PROBLEMS PLUS ¤ 717
one cycle to be
= 1
()[() − (−1)]. If we allow → ∞, we have
= lim
→∞
= 1
()[() − (−1)] = lim
→∞
= 1
()[() − (−1)] = lim
→∞
= 1
()[ () − (−1)]
=
(b) Let be the lower loop of the curve and the upper loop. Then = ∪ . is positively oriented, so from
Formula 16.4.5 we know the area of the lower loop in the -plane is given by − . is negatively oriented, so
the area of the upper loop is given by −− = . From part (a),
= = ∪ = + = − − ,
the difference of the areas enclosed by the two loops of .
°c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part.
NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.NOT FOR SALE
INSTRUCTOR USE ONLY
© Cengage Learning. All Rights Reserved.
[Show More]




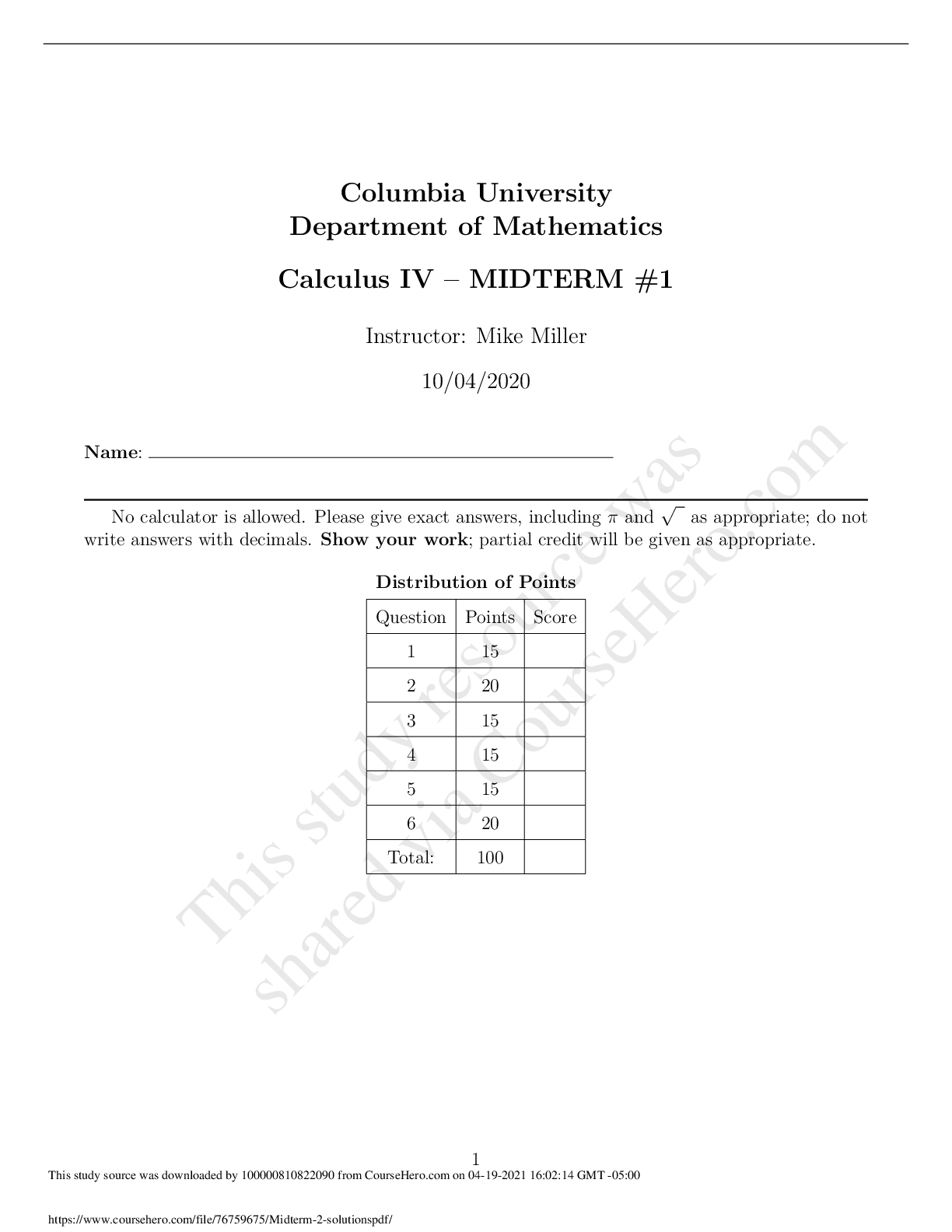




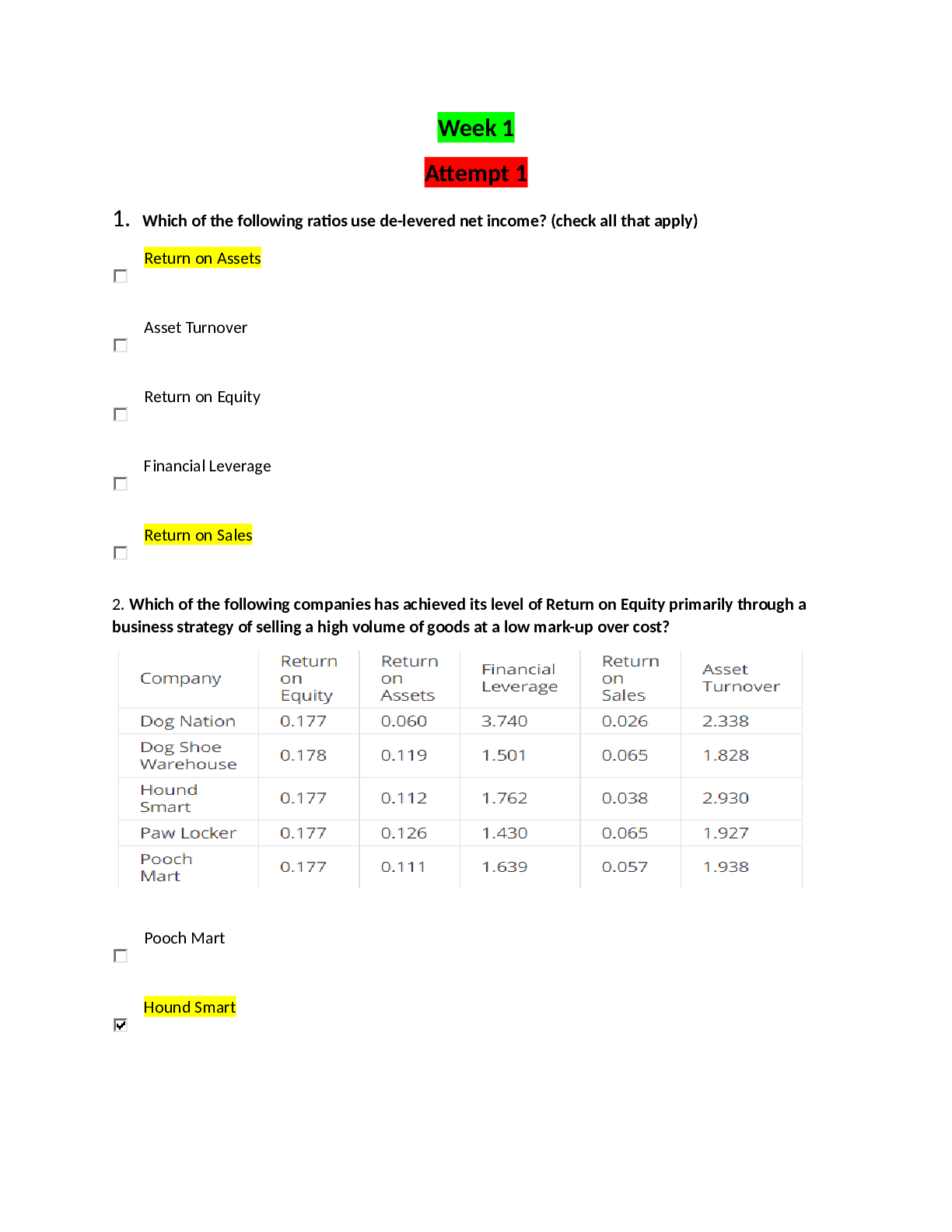
.png)
.png)
.png)
.png)