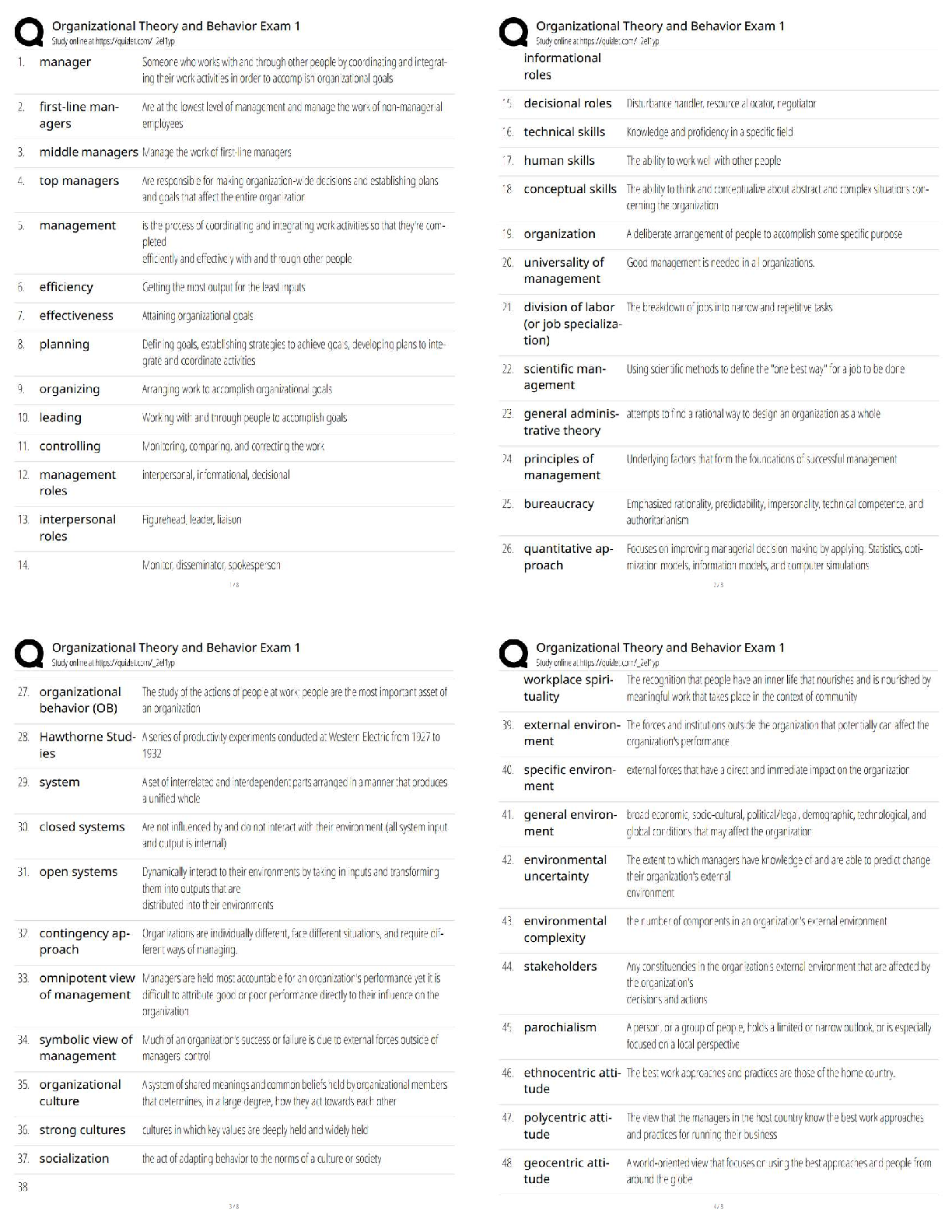
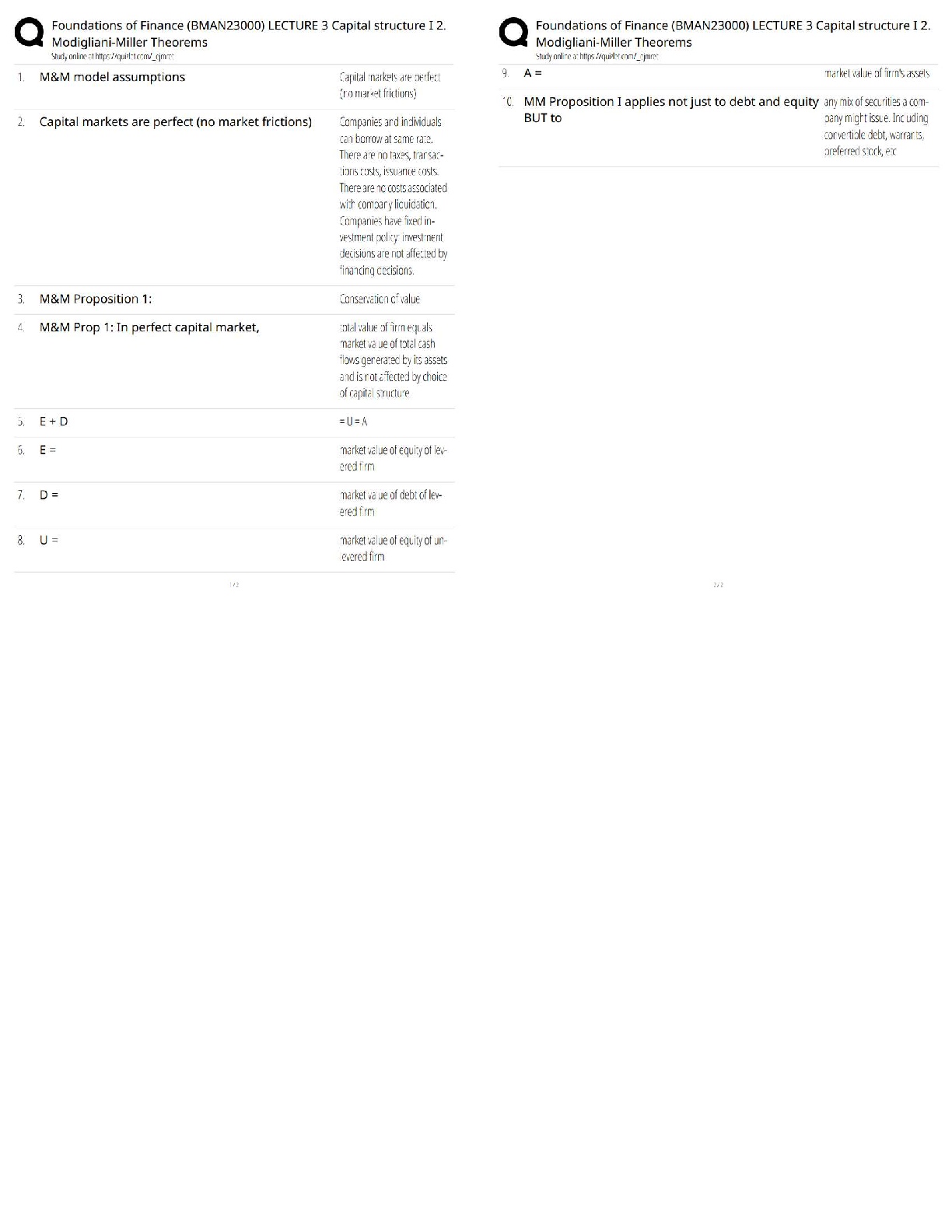
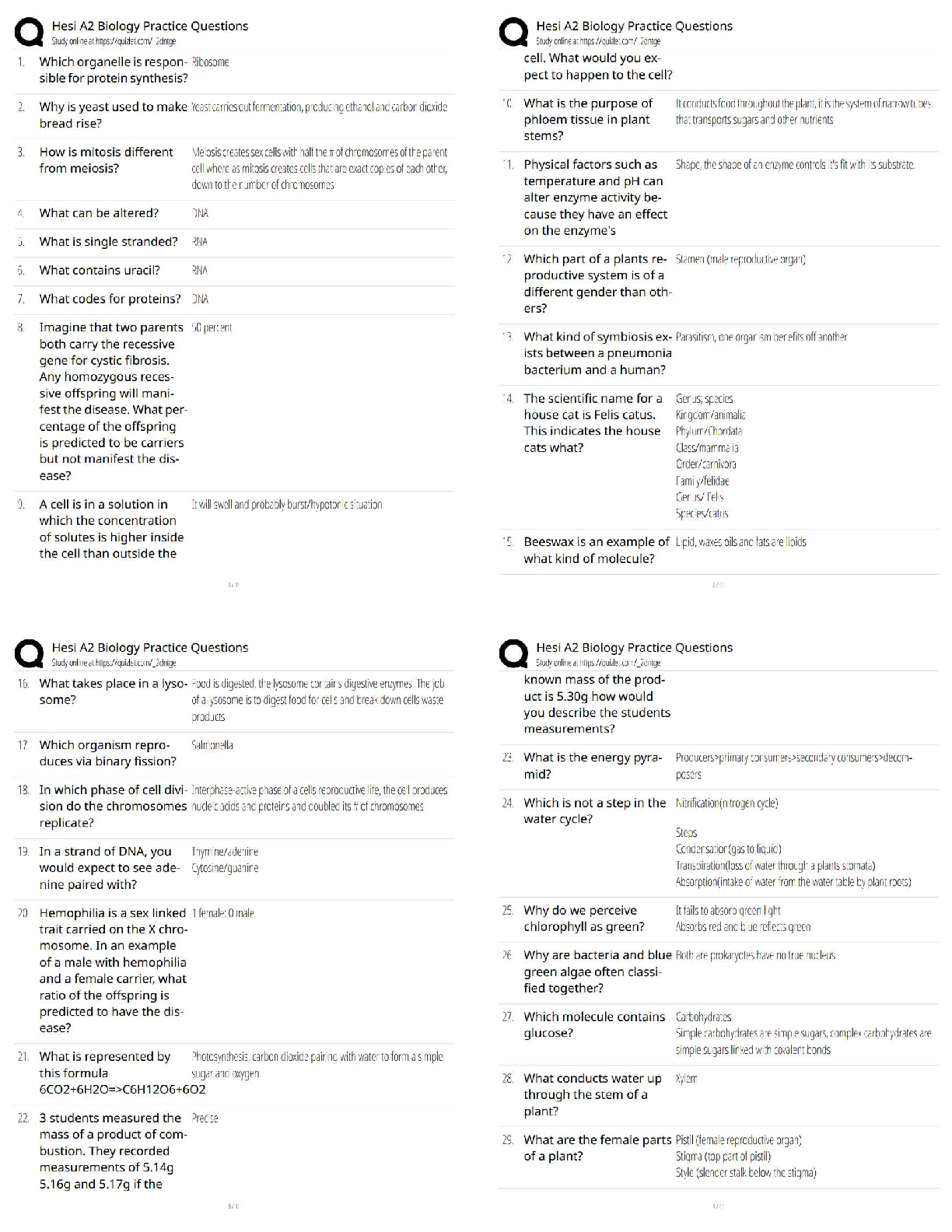
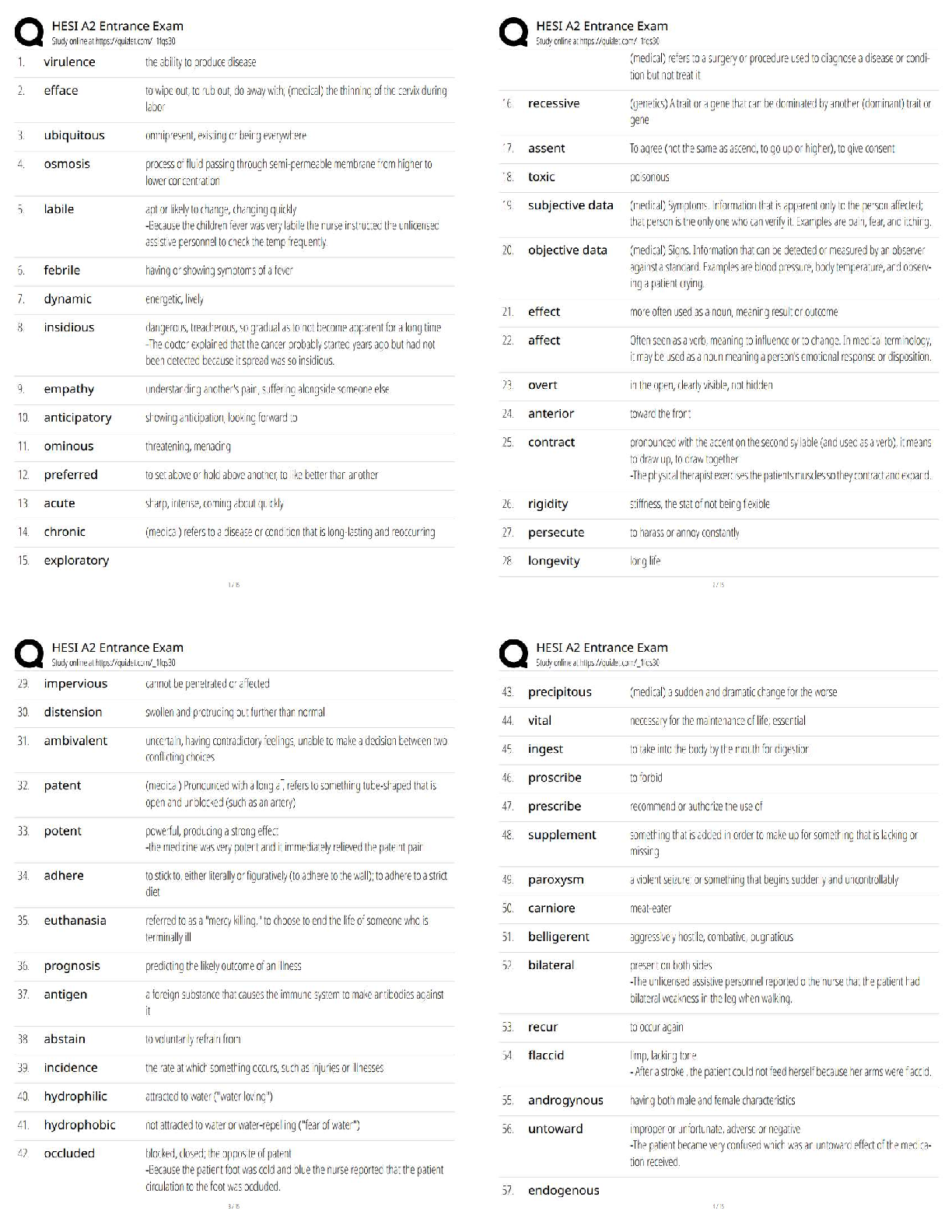
Calculus > QUESTIONS & ANSWERS > Stewart - Calculus ET 8e Chapter 17. All Answers (All)
Stewart - Calculus ET 8e Chapter 17. All Answers
Document Content and Description Below
1. Solve the initial-value problem. 2. Solve the boundary-value problem, if possible. 3. Solve the differential equation. 4. Solve the initial-value problem. 5. Solve the differential equation. 6 ... . Solve the differential equation. 7. Solve the differential equation. 8. Solve the initial-value problem. 9. Solve the boundary-value problem, if possible. 10. Solve the differential equation using the method of variation of parameters.Stewart - Calculus ET 8e Chapter 17 Form A © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 11. Solve the differential equation using the method of undetermined coefficients. 12. Solve the initial-value problem using the method of undetermined coefficients. 13. Solve the differential equation using the method of variation of parameters. 14. Solve the differential equation using the method of undetermined coefficients. 15. Solve the initial-value problem using the method of undetermined coefficients. 16. Solve the differential equation using the method of variation of parameters. 17. Solve the differential equation using the method of variation of parameters. 18. Solve the differential equation. 19. A spring with a mass of 2 kg has damping constant 14, and a force of N is required to keep the spring stretched m beyond its natural length. Find the mass that would produce critical damping. 20. A series circuit consists of a resistor an inductor with L = H, a capacitor with C = F, and a -V battery. If the initial charge and current are both 0, find the charge Q(t) at time t.Stewart - Calculus ET 8e Chapter 17 Form A © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17.Stewart - Calculus ET 8e Chapter 17 Form A © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 18. 19. 20.Stewart - Calculus ET 8e Chapter 17 Form B © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 1. Solve the initial-value problem. 2. Solve the initial-value problem. 3. Solve the differential equation using the method of variation of parameters. 4. Solve the differential equation using the method of undetermined coefficients. 5. A spring with a -kg mass has natural length m and is maintained stretched to a length of m by a force of N. If the spring is compressed to a length of m and then released with zero velocity, find the position of the mass at any time . 6. A spring with a mass of kg has damping constant 28 and spring constant . Find the damping constant that would produce critical damping. 7. Suppose a spring has mass M and spring constant k and let . Suppose that the damping constant is so small that the damping force is negligible. If an external force is applied (the applied frequency equals the natural frequency), use the method of undetermined coefficients to find the equation that describes the motion of the mass. 8. Use power series to solve the differential equation.. 9. Use power series to solve the differential equation.Stewart - Calculus ET 8e Chapter 17 Form B © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 10. The solution of the initial-value problem is called a Bessel function of order 0. Solve the initial - value problem to find a power series expansion for the Bessel function. 11. Solve the differential equation. 12. Solve the differential equation. 13. Solve the differential equation. 14. Solve the initial-value problem. 15. Solve the differential equation using the method of variation of parameters. 16. Solve the differential equation using the method of undetermined coefficients. 17. Solve the differential equation using the method of variation of parameters. 18. Solve the initial-value problem using the method of undetermined coefficients. 19. A spring with a mass of 2 kg has damping constant 14, and a force of N is required to keep the spring stretched m beyond its natural length. Find the mass that would produce critical damping.Stewart - Calculus ET 8e Chapter 17 Form B © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 20. A spring with a mass of 2 kg has damping constant 14, and a force of N is required to keep the spring stretched m beyond its natural length. The spring is stretched 1m beyond its natural length and then released with zero velocity. Find the position x(t) of the mass at any time t.Stewart - Calculus ET 8e Chapter 17 Form B © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. 2. 3. 4. 5. 6. 2340 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17.Stewart - Calculus ET 8e Chapter 17 Form B © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 18. 19. 20.Stewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 1. Solve the differential equation. a. b. c. d. e. ____ 2. Solve the differential equation. a. b. c. d. e. None of theseStewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 3. Solve the initial-value problem. a. b. c. d. e. ____ 4. Solve the initial-value problem. a. b. c. d. e. None of theseStewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 5. Solve the boundary-value problem, if possible. a. b. c. d. e. No solution ____ 6. Solve the differential equation. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 7. Graph the particular solution and several other solutions. a. c. b.Stewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 8. Solve the differential equation using the method of undetermined coefficients. a. b. c. d. e. ____ 9. Find a trial solution for the method of undetermined coefficients. Do not determine the coefficients. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 10. Solve the differential equation using the method of undetermined coefficients. a. b. c. d. e. ____ 11. Solve the differential equation using the method of variation of parameters. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 12. Solve the differential equation using the method of variation of parameters. a. b. c. d. e. ____ 13. Solve the differential equation using the method of variation of parameters. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 14. A spring with a 3-kg mass is held stretched 0.9 m beyond its natural length by a force of 30 N. If the spring begins at its equilibrium position but a push gives it an initial velocity of m/s, find the position x(t) of the mass after t seconds. a. b. c. d. e. ____ 15. A spring with a mass of kg has damping constant 28 and spring constant . Find the damping constant that would produce critical damping. a. 6 b. 6 130 c. 780 6 d. 24 195 e.Stewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 16. A series circuit consists of a resistor , an inductor with , a capacitor with , and a generator producing a voltage of If the initial charge is and the initial current is 0, find the charge at time t. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 17. A spring with a mass of 2 kg has damping constant 8 and spring constant 80. Graph the position function of the mass at time t if it starts at the equilibrium position with a velocity of 2 m/s. a. c. b.Stewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 18. Suppose a spring has mass M and spring constant k and let . Suppose that the damping constant is so small that the damping force is negligible. If an external force is applied (the applied frequency equals the natural frequency), use the method of undetermined coefficients to find the equation that describes the motion of the mass. a. b. c. d. e. ____ 19. Use power series to solve the differential equation. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 20. The solution of the initial-value problem is called a Bessel function of order 0. Solve the initial - value problem to find a power series expansion for the Bessel function. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 17 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. C 2. A 3. C 4. C 5. A 6. C 7. B 8. B 9. B 10. E 11. B 12. D 13. E 14. A 15. C 16. C 17. B 18. B 19. B 20. CStewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 1. Solve the differential equation. a. b. c. d. e. ____ 2. Solve the boundary-value problem, if possible. a. b. c. d. e. No solutionStewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 3. Solve the differential equation. a. b. c. d. e.Stewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 4. Solve the initial-value problem. . a. b. c. d. e. ____ 5. Solve the initial-value problem. a. b. c. d. e.Stewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 6. Solve the initial-value problem. a. b. c. d. e. None of these ____ 7. Solve the boundary-value problem, if possible. a. b. c. d. e. No solutionStewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 8. Graph the particular solution and several other solutions. a. c. b.Stewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 9. Solve the differential equation using the method of undetermined coefficients. a. b. c. d. e. ____ 10. Solve the differential equation using the method of undetermined coefficients. a. b. c. d. e.Stewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 11. Solve the differential equation using the method of variation of parameters. a. b. c. d. e. ____ 12. A spring with a -kg mass has natural length m and is maintained stretched to a length of m by a force of N. If the spring is compressed to a length of m and then released with zero velocity, find the position of the mass at any time . a. b. c. d. e.Stewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 13. A spring with a 3-kg mass is held stretched 0.9 m beyond its natural length by a force of 30 N. If the spring begins at its equilibrium position but a push gives it an initial velocity of m/s, find the position x(t) of the mass after t seconds. a. b. c. d. e. ____ 14. A spring with a mass of kg has damping constant 28 and spring constant . Find the damping constant that would produce critical damping. a. 288 3 b. 48 3 c. 2304 d. 9 e.Stewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 15. A series circuit consists of a resistor , an inductor with , a capacitor with , and a -V battery. If the initial charge is 0.0008 C and the initial current is 0, find the current I(t) at time t. a. b. c. d. e.Stewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 16. A spring with a mass of 2 kg has damping constant 8 and spring constant 80. Graph the position function of the mass at time t if it starts at the equilibrium position with a velocity of 2 m/s. a. c. b.Stewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 17. Suppose a spring has mass M and spring constant k and let . Suppose that the damping constant is so small that the damping force is negligible. If an external force is applied (the applied frequency equals the natural frequency), use the method of undetermined coefficients to find the equation that describes the motion of the mass. a. b. c. d. e. ____ 18. Use power series to solve the differential equation. a. b. c. d. e.Stewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 19. Use power series to solve the differential equation. a. b. c. d. e.Stewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 20. The solution of the initial-value problem is called a Bessel function of order 0. Solve the initial - value problem to find a power series expansion for the Bessel function. a. b. c. d. e.Stewart - Calculus ET 8e Chapter 17 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. A 2. D 3. E 4. A 5. B 6. B 7. A 8. B 9. C 10. E 11. B 12. D 13. C 14. C 15. B 16. B 17. C 18. A 19. C 20. CStewart - Calculus ET 8e Chapter 17 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 1. Solve the boundary-value problem, if possible. Select the correct answer. a. b. c. d. e. No solution 2. Solve the differential equation. 3. Solve the differential equation. ____ 4. Solve the initial-value problem. Select the correct answer. . a. b. c. d. e. 5. Solve the differential equation.Stewart - Calculus ET 8e Chapter 17 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 6. Solve the initial-value problem. Select the correct answer. a. b. c. d. e. 7. Solve the initial-value problem. 8. Solve the boundary-value problem, if possible. ____ 9. Solve the differential equation. Select the correct answer. a. b. c. d. e.Stewart - Calculus ET 8e Chapter 17 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 10. Solve the differential equation using the method of undetermined coefficients. ____ 11. Solve the differential equation using the method of variation of parameters. Select the correct answer. a. b. c. d. e. 12. A spring with a -kg mass has natural length m and is maintained stretched to a length of m by a force of N. If the spring is compressed to a length of m and then released with zero velocity, find the position of the mass at any time . ____ 13. A spring with a mass of kg has damping constant 28 and spring constant . Find the damping constant that would produce critical damping. Select the correct answer. a. 36 195 b. 2340 c. d. 9 e. 6 195 14. A series circuit consists of a resistor , an inductor with , a capacitor with , and a generator producing a voltage of If the initial charge is and the initial current is 0, find the charge at time t.Stewart - Calculus ET 8e Chapter 17 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 15. A spring with a mass of 2 kg has damping constant 8 and spring constant 80. Graph the position function of the mass at time t if it starts at the equilibrium position with a velocity of 2 m/s. ____ 16. Suppose a spring has mass M and spring constant k and let . Suppose that the damping constant is so small that the damping force is negligible. If an external force is applied (the applied frequency equals the natural frequency), use the method of undetermined coefficients to find the equation that describes the motion of the mass. Select the correct answer. a. b. c. d. e. 17. Use power series to solve the differential equation..Stewart - Calculus ET 8e Chapter 17 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 18. Use power series to solve the differential equation. Select the correct answer. a. b. c. d. e. 19. Use power series to solve the differential equation. 20. The solution of the initial-value problem is called a Bessel function of order 0. Solve the initial - value problem to find a power series expansion for the Bessel function.Stewart - Calculus ET 8e Chapter 17 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. C 2. 3. 4. A 5. 6. A 7. 8. 9. C 10. 11. A 12. 13. B 14. 15. 16. C 17. 18. CStewart - Calculus ET 8e Chapter 17 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 19. 20.Stewart – Calculus ET 8e Chapter 17 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 1. Solve the differential equation. Select the correct answer. a. b. c. d. e. 2. Solve the initial-value problem. ____ 3. Solve the differential equation. Select the correct answer. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 17 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 4. Solve the differential equation. 5. Solve the initial-value problem. . ____ 6. Solve the initial-value problem. Select the correct answer. a. b. c. d. e. 7. Solve the differential equation. 8. Find f by solving the initial value problem. ; , 9. Solve the differential equation using the method of variation of parameters.Stewart – Calculus ET 8e Chapter 17 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 10. Graph the particular solution and several other solutions. Select the correct answer. a. c. b. 11. Solve the differential equation using the method of undetermined coefficients. 12. Find a trial solution for the method of undetermined coefficients. Do not determine the coefficients.Stewart – Calculus ET 8e Chapter 17 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 13. Find a trial solution for the method of undetermined coefficients. Do not determine the coefficients. 14. Solve the differential equation using the method of undetermined coefficients. ____ 15. Solve the differential equation using the method of variation of parameters. Select the correct answer. a. b. c. d. e. 16. Solve the differential equation using the method of variation of parameters.Stewart – Calculus ET 8e Chapter 17 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 17. A spring with a -kg mass has natural length m and is maintained stretched to a length of m by a force of N. If the spring is compressed to a length of m and then released with zero velocity, find the position of the mass at any time . Select the correct answer. a. b. c. d. e. ____ 18. A spring with a mass of kg has damping constant 28 and spring constant . Find the damping constant that would produce critical damping. Select the correct answer. a. 36 195 b. 2340 c. d. 9 e. 6 195 19. Suppose a spring has mass M and spring constant k and let . Suppose that the damping constant is so small that the damping force is negligible. If an external force is applied (the applied frequency equals the natural frequency), use the method of undetermined coefficients to find the equation that describes the motion of the mass. 20. Use power series to solve the differential equation.Stewart – Calculus ET 8e Chapter 17 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. C 2. 3. E 4. 5. 6. A 7. 8. 2 3 2 + 2 16 3 x 10 9. 10. B 11. 12. 13. 14. 15. D 16. 17. E 18. B 19. 20.Stewart – Calculus ET 8e Chapter 17 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 1. Solve the differential equation. ____ 2. Solve the differential equation. Select the correct answer. a. b. c. d. e. 3. Solve the differential equation. 4. Solve the initial-value problem. ____ 5. Solve the differential equation. Select the correct answer. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 17 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 6. Solve the differential equation using the method of variation of parameters. 7. Graph the particular solution and several other solutions. 8. Solve the differential equation using the method of undetermined coefficients. ____ 9. Find a trial solution for the method of undetermined coefficients. Do not determine the coefficients. Select the correct answer. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 17 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 10. Solve the differential equation using the method of undetermined coefficients. 11. Solve the differential equation using the method of variation of parameters. ____ 12. Solve the differential equation using the method of variation of parameters. Select the correct answer. a. b. c. d. e. 13. A spring with a -kg mass has natural length m and is maintained stretched to a length of m by a force of N. If the spring is compressed to a length of m and then released with zero velocity, find the position of the mass at any time .Stewart – Calculus ET 8e Chapter 17 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 14. A spring has a mass of kg and its damping constant is . The spring starts from its equilibrium position with a velocity of m/s. Graph the position function for the spring constant . Select the correct answer. a. c. b. 15. A spring with a 3-kg mass is held stretched 0.9 m beyond its natural length by a force of 30 N. If the spring begins at its equilibrium position but a push gives it an initial velocity of m/s, find the position x(t) of the mass after t seconds. 16. A series circuit consists of a resistor , an inductor with , a capacitor with , and a -V battery. If the initial charge is 0.0008 C and the initial current is 0, find the current I(t) at time t. 17. A series circuit consists of a resistor , an inductor with , a capacitor with , and a generator producing a voltage of If the initial charge is and the initial current is 0, find the charge at time t.Stewart – Calculus ET 8e Chapter 17 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 18. A spring with a mass of 2 kg has damping constant 8 and spring constant 80. Graph the position function of the mass at time t if it starts at the equilibrium position with a velocity of 2 m/s. Select the correct answer. a. c. b. 19. Use power series to solve the differential equation.. 20. The solution of the initial-value problem is called a Bessel function of order 0. Solve the initial - value problem to find a power series expansion for the Bessel function.Stewart – Calculus ET 8e Chapter 17 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. 2. C 3. 4. 5. C 6. 7. 8. 9. B 10. 11. 12. A 13. 14. A 15. 16. 17. 18. BStewart – Calculus ET 8e Chapter 17 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 19. 20.Stewart - Calculus ET 8e Chapter 17 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 1. Solve the differential equation. Select the correct answer. a. b. c. d. e. 2. Solve the initial-value problem. 3. Solve the boundary-value problem, if possible. 4. Solve the differential equation.Stewart - Calculus ET 8e Chapter 17 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 5. Solve the initial-value problem. Select the correct answer. . a. b. c. d. e. 6. Solve the initial-value problem. 7. Solve the boundary-value problem, if possible. 8. Solve the differential equation using the method of undetermined coefficients.Stewart - Calculus ET 8e Chapter 17 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 9. Solve the differential equation using the method of undetermined coefficients. Select the correct answer. a. b. c. d. e. 10. Solve the differential equation using the method of variation of parameters. 11. Solve the differential equation using the method of variation of parameters. ____ 12. A spring with a -kg mass has natural length m and is maintained stretched to a length of m by a force of N. If the spring is compressed to a length of m and then released with zero velocity, find the position of the mass at any time . Select the correct answer. a. b. c. d. e.Stewart - Calculus ET 8e Chapter 17 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 13. A spring has a mass of kg and its damping constant is . The spring starts from its equilibrium position with a velocity of m/s. Graph the position function for the spring constant . 14. A spring with a mass of 2 kg has damping constant 8 and spring constant 80. Graph the position function of the mass at time t if it starts at the equilibrium position with a velocity of 2 m/s. 15. Suppose a spring has mass M and spring constant k and let . Suppose that the damping constant is so small that the damping force is negligible. If an external force is applied (the applied frequency equals the natural frequency), use the method of undetermined coefficients to find the equation that describes the motion of the mass. ____ 16. Use power series to solve the differential equation. Select the correct answer. a. b. c. d. e. 17. Use power series to solve the differential equation. 18. Use power series to solve the differential equation.Stewart - Calculus ET 8e Chapter 17 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 19. Use power series to solve the differential equation. Select the correct answer. a. b. c. d. e. 20. The solution of the initial-value problem is called a Bessel function of order 0. Solve the initial - value problem to find a power series expansion for the Bessel function.Stewart - Calculus ET 8e Chapter 17 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. B 2. 3. 4. 5. D 6. 7. 8. 9. B 10. 11. 12. B 13.Stewart - Calculus ET 8e Chapter 17 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 14. 15. 16. D 17. 18. 19. C 20. [Show More]
Last updated: 3 years ago
Preview 1 out of 63 pages

Buy this document to get the full access instantly
Instant Download Access after purchase
Buy NowInstant download
We Accept:

Reviews( 0 )
$10.00
Can't find what you want? Try our AI powered Search
Document information
Connected school, study & course
About the document
Uploaded On
Jan 15, 2020
Number of pages
63
Written in
All
Additional information
This document has been written for:
Uploaded
Jan 15, 2020
Downloads
0
Views
160





.png)
.png)
.png)
.png)
.png)