CS 421 Theory of computing CS421 HW3B (based on Week 10 - 11) – Other Practical Issues | California State University, San Marcos

Document Content and Description Below

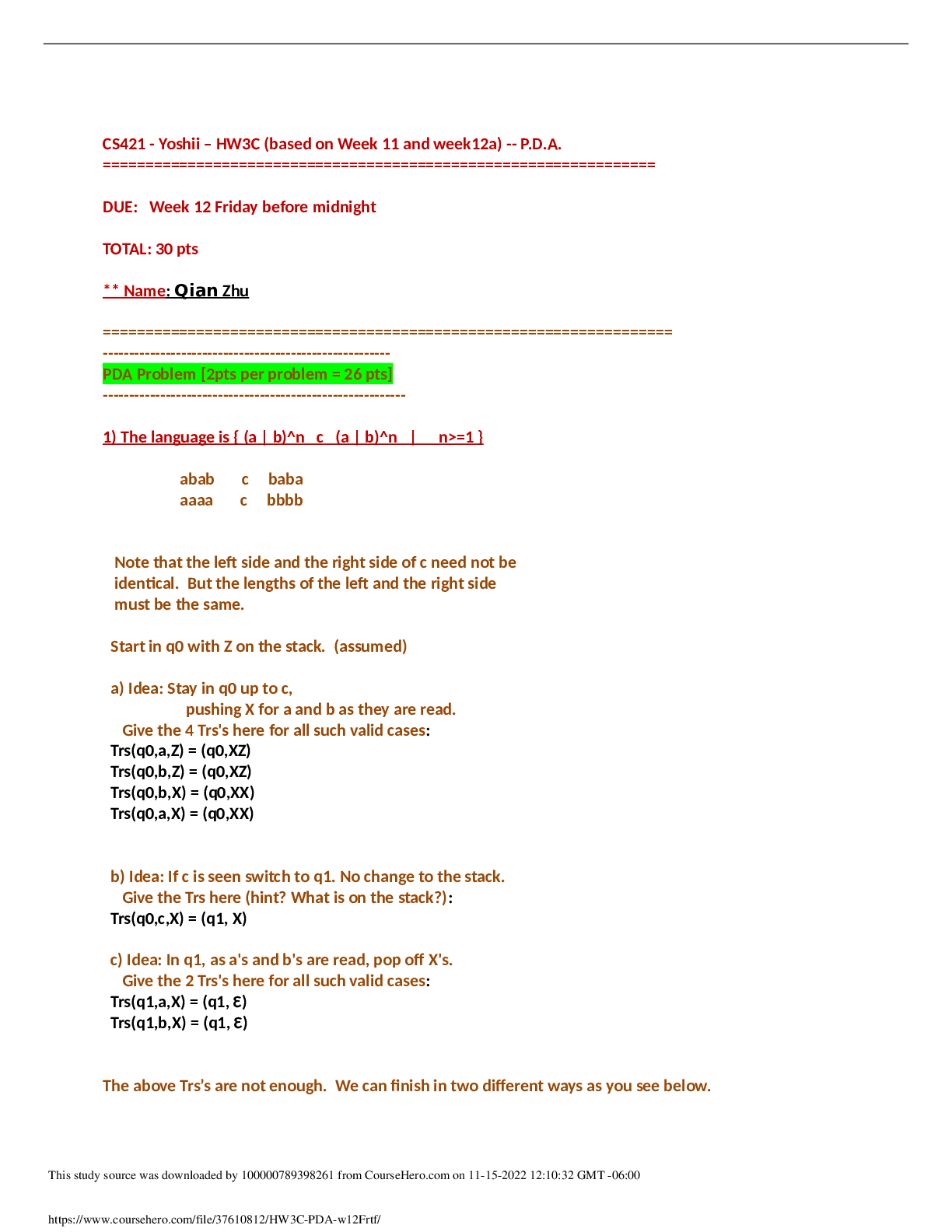
California State University, San Marcos CS 421   Theory of computing CS421 - Yoshii – HW3B (based on Week 10 - 11) – Other Practical Issues Induction and CNF Always Use Black for your answ ... ers DUE: Week 11 Friday before midnight TOTAL: 20 pts ** Name: **Qian Zhu -------------------------------------------------------------------------------------------------------------------------- 1) Proving that G matches L: [.5pts per prompt = 5pts] Finish the Inductive Proof from week 10. L = {w | w has an equal number of a’s and b’s} --------------------------------------------------------------------------------------------------------------------------- // we have 3 non-terminals 1 S -> aB // starts with a 2 S -> bA // starts with b // comes to A after starting with b. A means balance that b with a. 3 A -> a 4 A -> aS 5 A -> bAA // comes to B after starting with a. B means balance that a with b. 6 B -> b 7 B -> bS 8 B -> aBB We were doing induction to prove that G can generate all strings of L. GIVEN ASSUMPTIONS when |w| <= k-1 T1. S can =*=> w if w consists of an equal number of a's and b's T2. A can =*=> w if w has one more a than b's T3. B can =*=> w if w has one more b than a`s You must now prove the properties (T2 and T3) of A and B for the |w| = k step. Please fill in the template below. For Why questions, refer to the above given assumptions. E.g. “Using the given assumption T1.” T2 step for A: · Prove that if w has one more a than b's, A can =*=> w where |w| = k (describe w in terms of shorter strings z, y1 and y2) w looks like: a<z> or b<y1 and y2> [.5] Thus z and y1 and y2 have properties such that: z: <what does it have?>has equal a’s and b’s <how long is it?> k-1 each y1 and y2: <what does it have?>has two more a’s than b’s <how long is it?> k-1 What non-terminal can derive z? S Why? Based on the assumption on S. What non-terminal can derive each y? B Why? Based on the assumption on B. Thus A =*=> w: Starting with these rules from A: ** starts with a which follow by z or starts with b which follow y1 and y2 T3 step for B: · Prove that if w has one more b than a's, B can =*=> w where |w| = k Has to be done for the proof to be complete. But it is not required for this HW. -------------------------------------------------------------------------------------------- 2) Making it CNF – prep G for CYK parsing or analysis [15 pts] -------------------------------------------------------------------------------------------- We will start with 1. S -> a A B b 2. S -> e E Follow the following instructions step by step and answer each question. You may refer to the rule numbers in answering “which rules” questions! a) Remove all useless rules. [2pts] 1- Start bottom up from terminal strings.[1] o Which rules derive string o Which rules do not derive strings and should be removed 2- Then start top down from S.[1] o Which rules are reachable from S o Which rules are not reachable from S and should be removed b) Make it epsilon-free. [4pts] 1. S -> a A B b 5. B -> d d 1- Which non-terminals go directly or indirectly to epsilon (?? =*=> epsilon) [1] 2- Which rules use such non-terminals on the right side [1]?2 3- List all the ways to make such non-terminals disappear from the right side [1]. Newly added rules are: 4- What epsilon-rules will now be removed (they go directly to epsilon)[1]? 3 c) Make it chain-free (no <non term>-><non term>). [4pts] 1. S -> a A B b 2. S -> a B b 3. A -> C C 4. A -> C 5. C -> x 6. B -> d d 1- List all chain derivations (i.e. <non-term> =*=> <non-term>)[1]: 2- For each chain, add rule(s) to skip the right side non-terminal [1]. List added rules: 3- Delete all chain rules. List the ones to delete [1]: 4- Did any rule become useless and need to be removed? Which ones [1]? 2 d) Make it stratified (no non-terminal terminal mixture).[3pts] 1. S -> a A B b 2. S -> a B b 3. A -> C C 4. A -> x 5. C -> x 6. B -> d d 1. Add N#-><terminal> rule for each terminal (a,b,d,x) [1] (i.e. use N1, N2, etc.): 2. Stratify mixed rules. [1] Change this mixed rule: To what? Change this mixed rule: To what? Change B -> d d to what? 3. List the resulting grammar: [1] (should have only one terminal or only non-terminals on the RHS) e) Make the result of (d), binary (i.e. 2 non-terms) [2pts] 1- Change this rule: To what? Change this rule: To what? 2- Final Result is: [Show More]

Last updated: 7 months ago

Preview 1 out of 5 pages