Theory of Computing > QUESTIONS & ANSWERS > CS 421 Theory of computing CS421 HW 2C (based week 5-6) RE to DFA Automatic California State Unive (All)

CS 421 Theory of computing CS421 HW 2C (based week 5-6) RE to DFA Automatic California State University, San Marcos

Document Content and Description Below

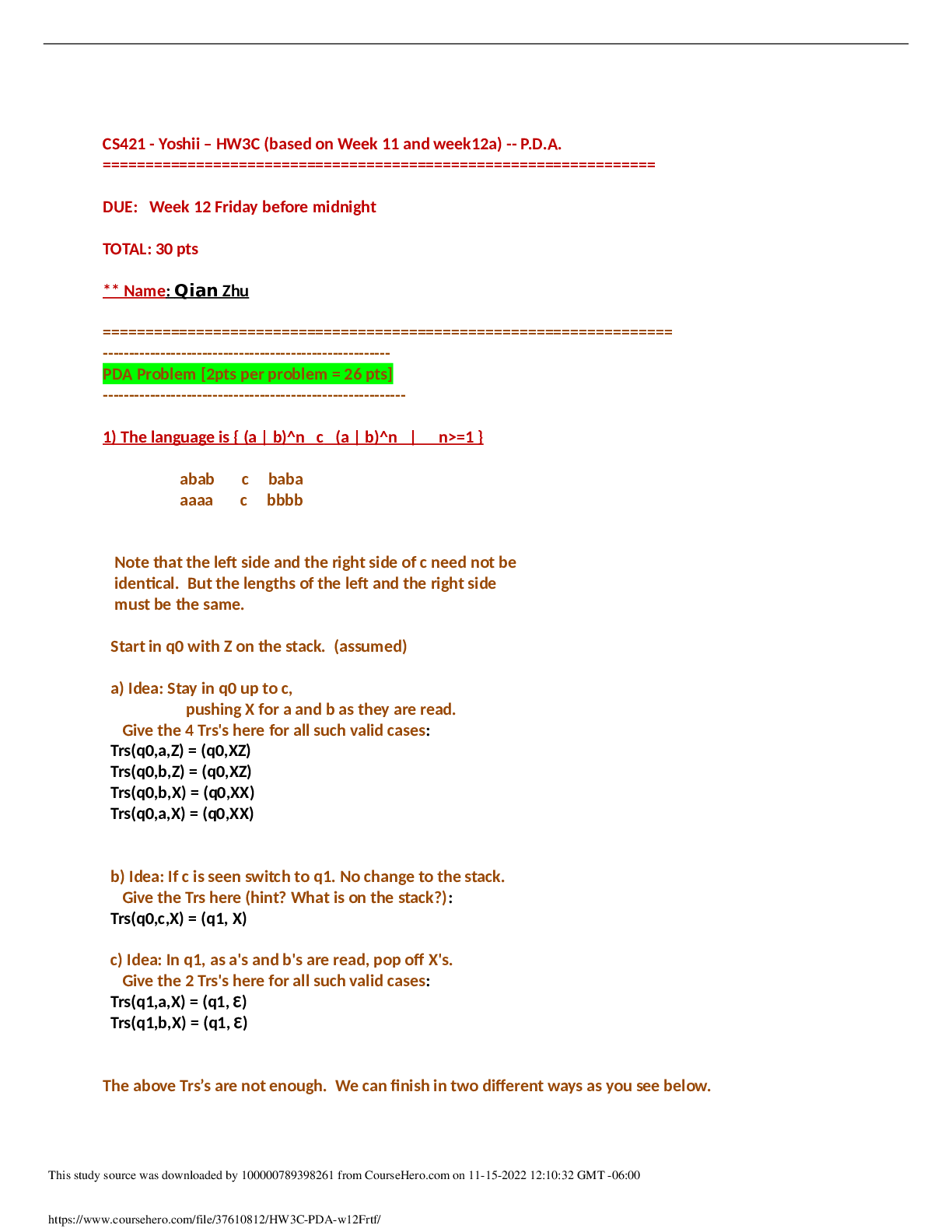
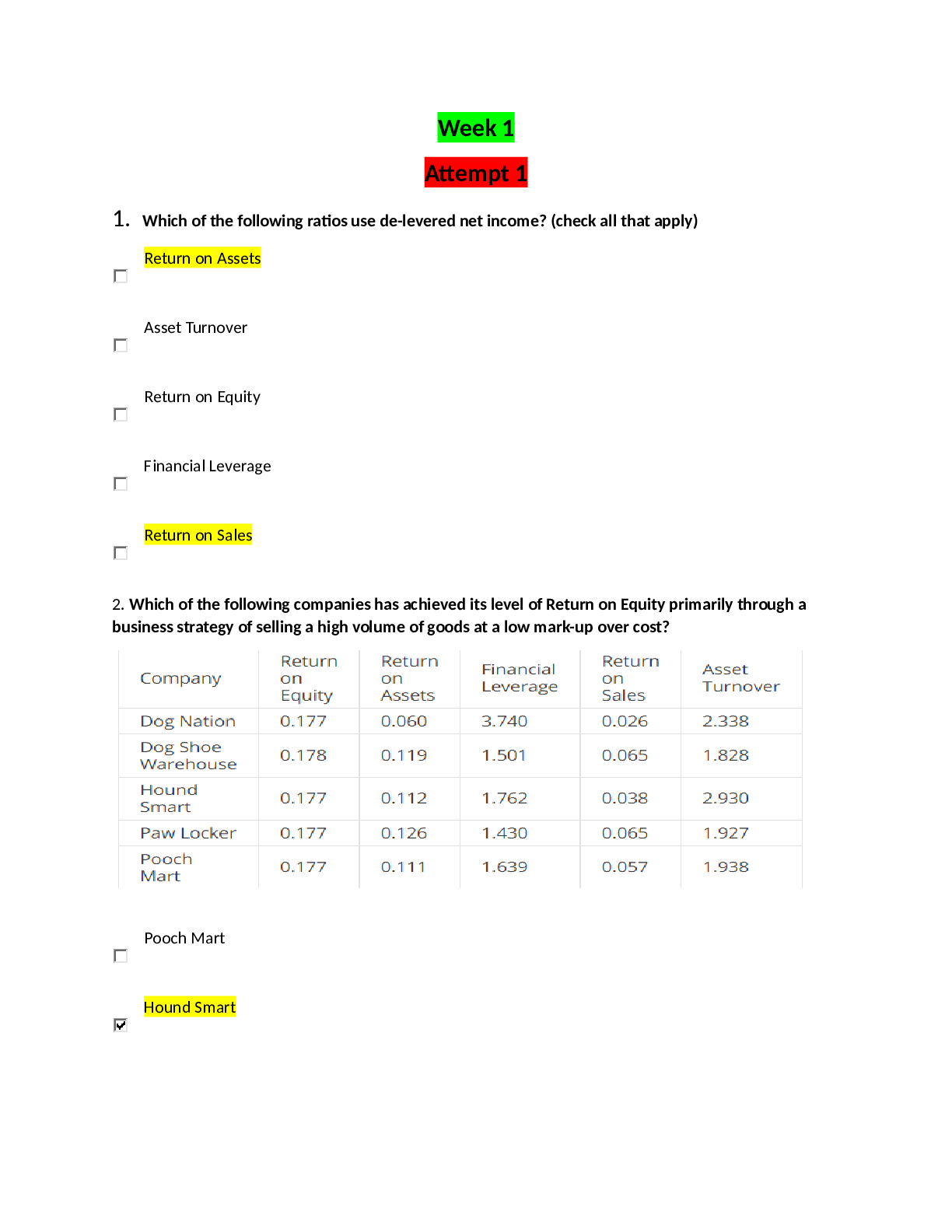
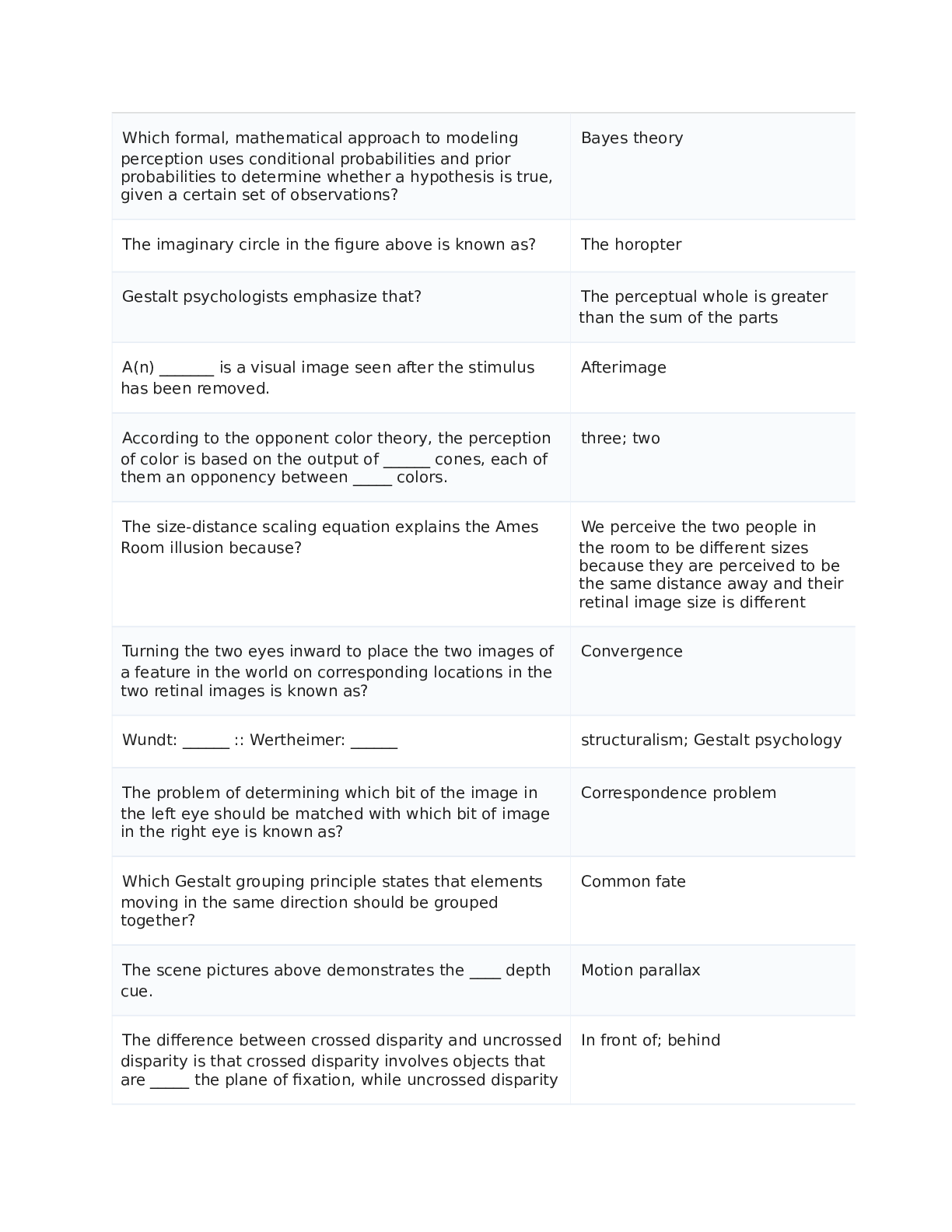
California State University, San Marcos CS 421 Theory of computing CS421 - Yoshii - HW 2C (based week 5-6) RE to DFA Automatic =============================================================... ======== DUE: Week 7 Friday before midnight TOTAL: 30 pts ** Name: **Qian Zhu Use my demo programs for these to verify your answers first!!! ------------------------------------------------------------------------------------- Problem 1: RE -> NFA-e (From week5a) [2pts per machine = 12 pts] ------------------------------------------------------------------------------------ Give NFA-e for the following REs. Show component machines first and then show all steps of connecting these machines using the methods described in week6a notes. Hand-drawing is OK (just insert into this file). [2pts per machine] Do not use any simplification. Having many e-moves is what we want. The following is for b(a|bb)^* No state numbers are needed for components. HINT: Put M1 in front of M5 connected with a blank arrow and then give state numbers (make sure state numbers are unique) ------------------------------------------------------------------- Problem 2: NFA-e -> NFA (From week5b) [10 pts] --------------------------------------------------------------------- Remove e-moves from the following. I indicate e-moves with “e” on arrows. i.e. the NFA is: Trs(q8,e) = q9 final 1) Please compute Trs-e for each state-symbol pair: [6pts] Trs-e(q0, e* a e*) = { Trs-e(q0, e* b e*) = { Trs-e(q1, e* a e*) = { Trs-e(q1, e* b e*) = { Trs-e(q2, e* a e*) = { Trs-e(q2, e* b e*) = { nothing} etc. Continue for all state-symbol pairs. 2) Then draw the NFA based on the above results without simplification (hand-drawing is OK but insert here):[4pts] ----------------------------------------------------------------------- Problem 3: NFA -> DFA (From week6a) [8 pts] ----------------------------------------------------------------------- Before we can implement a scanner, your machine has to become deterministic. NFA: q0 loop on 0,1 q2 loop on 0,1. q2 is final. (q0) --- 0 -----------> (q1) --- 1 ---> ((q2)) q1 loop on 0,1 Trs(q0, 0) = {q0, q1} Trs(q0, 1) = {q0} Trs(q1, 0) = {q1} Trs(q1, 1) = {q1, q2} Trs(q2, 0) = {q2} Trs(q2, 1) = {q2} Then from each new resulting state, give Trs on 0 and 1 And finish this until there are no more new states. -- List all the Trs's here [4pts] -- Then draw the resulting DFA showing all the Trs’s and mark all final states [2pts] : B) What is the language accepted by this DFA? To answer, give its RE matching your DFA [2pts] : [Show More]

Last updated: 1 month ago

Preview 1 out of 5 pages

Buy Now

Instant download

We Accept: