CH 16 - Markov Processes. Questions and Answers

Document Content and Description Below

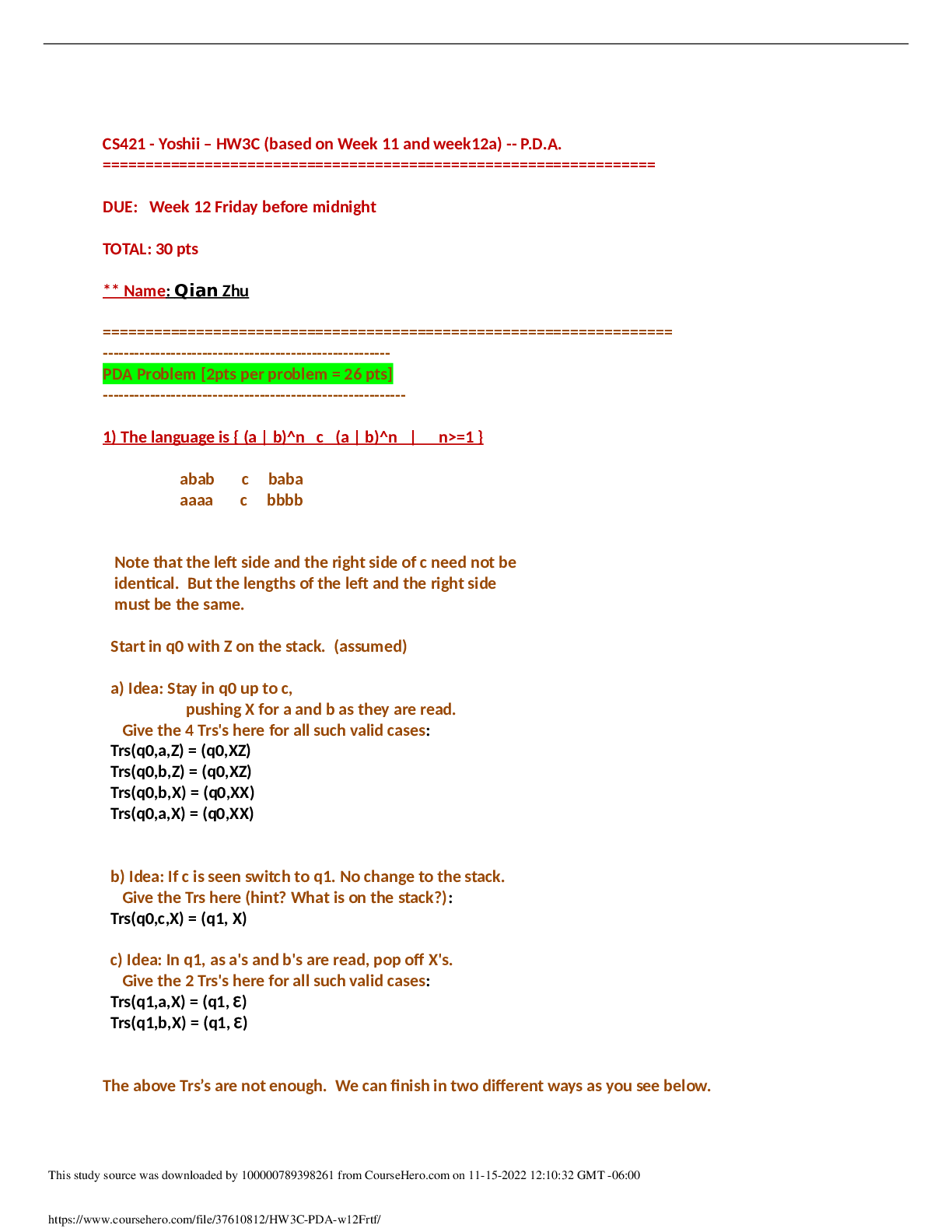
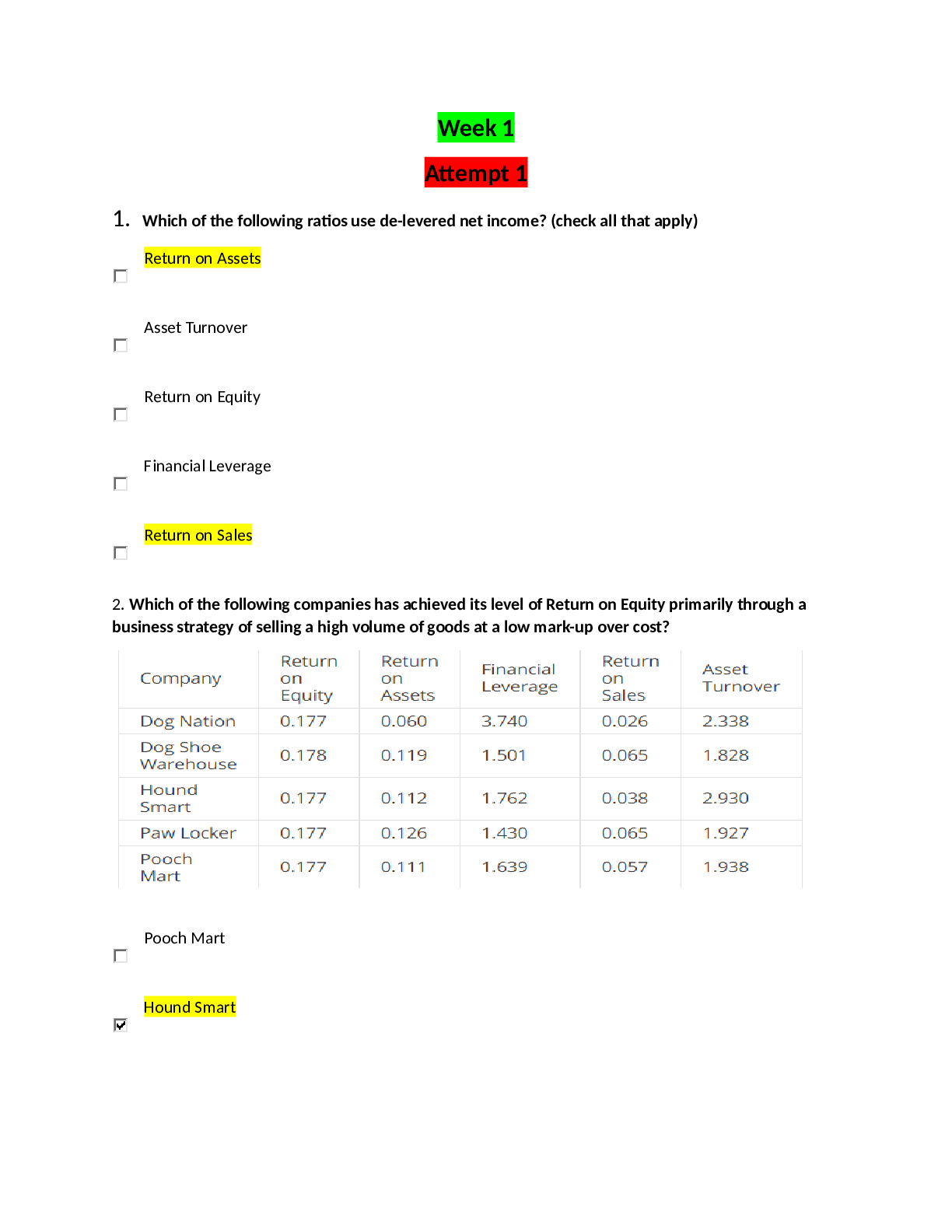
True / False 1. Markov processes use historical probabilities. a. True b. False 2. All entries in a matrix of transition probabilities sum to 1. a. True b. False 3. Al... l Markov chain transition matrices have the same number of rows as columns. a. True b. False 4. A unique matrix of transition probabilities should be developed for each customer. a. True b. False 5. The probability that a system is in state 2 in the fifth period is π5(2). a. True b. False 6. The fundamental matrix is derived from the matrix of transition probabilities and is relatively easy to compute for Markov processes with a small number of states. a. True b. False 7. Steady-state probabilities are independent of initial state. a. True b. False 8. A Markov chain cannot consist of all absorbing states. a. True b. False 9. If an absorbing state exists, then the probability that a unit will ultimately move into the absorbing state is given by the steady-state probability. a. True b. False 10. All Markov chains have steady-state probabilities. a. True b. False 11. All entries in a row of a matrix of transition probabilities sum to 1. a. True b. False 12. A state i is a transient state if there exists a state j that is reachable from i, but the state i is not reachable from state j. a. True b. False 13. When absorbing states are present, each row of the transition matrix corresponding to an absorbing state will have a single 1 and all other probabilities will be 0. a. True b. False 14. For Markov processes having the memoryless property, the prior states of the system must be considered in order to predict the future behavior of the system. a. True b. False 15. When absorbing states are present, each row of the transition matrix corresponding to an absorbing state will have a single 1 and all other probabilities will be 0. a. True b. False 16. Transition probabilities are conditional probabilities. a. True b. False 17. A state, i, is an absorbing state if, when i = j, pij = 1. a. True b. False 18. If a Markov chain has at least one absorbing state, steady-state probabilities cannot be calculated. a. True b. False 19. State j is an absorbing state if pij = 1. a. True b. False 20. A state is said to be absorbing if the probability of making a transition out of that state is zero. a. True b. False 21. Transition probabilities indicate that a customer moves, or makes a transition, from a state in a given period to each state in the following period. a. True b. False Multiple Choice 22. In Markov analysis, we are concerned with the probability that the a. state is part of a system. b. system is in a particular state at a given time. c. time has reached a steady state. d. transition will occur. 23. For a situation with weekly dining at either an Italian or Mexican restaurant, a. the weekly visit is the trial and the restaurant is the state. b. the weekly visit is the state and the restaurant is the trial. c. the weekly visit is the trend and the restaurant is the transition. d. the weekly visit is the transition and the restaurant is the trend. 24. A transition probability describes a. the probability of a success in repeated, independent trials. b. the probability a system in a particular state now will be in a specific state next period. c. the probability of reaching an absorbing state. d. None of these are correct. 25. The probability of going from state 1 in period 2 to state 4 in period 3 is a. p12. b. p23. c. p14. d. p43. 26. The probability that a system is in a particular state after a large number of periods is a. independent of the beginning state of the system. b. dependent on the beginning state of the system. c. equal to one half. d. the same for every ending system. 27. At steady state, a. π1(n + 1) > π1(n). b. π1 = π2. c. π1 + π2 ≥ 1. d. π1(n + 1) = π1. 28. Markov process trials a. are used to describe future behavior of the system. b. are used to optimize the system. c. lead to higher-order decision making. d. All of these are correct. 29. If the probability of making a transition from a state is 0, then that state is called a(n) a. steady state. b. final state. c. origin state. d. absorbing state. 30. Absorbing state probabilities are the same as a. steady-state probabilities. b. transition probabilities. c. fundamental probabilities. d. None of these are correct. 31. The probability of reaching an absorbing state is given by the a. R matrix. b. NR matrix. c. Q matrix. d. (I − Q)−1 matrix. 32. Markov process models a. study system evolution over repeated trials. b. often study successive time periods. c. are often used when the state of the system in any particular period cannot be determined with certainty. d. All of these are correct. 33. The probability of making a transition from state i in a given period to state j in the next period is denoted as a. Pij. b. P = [i – j]. c. P( )ij. d. None of these are correct. Subjective Short Answer 34. Calculate the steady-state probabilities for this transition matrix. 35. Two airlines offer conveniently scheduled flights to the airport nearest your corporate headquarters. Historically, flights have been scheduled as reflected in this transition matrix. Current Next Flight Flight Airline A Airline B Airline A 0.6 0.4 Airline B 0.2 0.8 a. If your last flight was on B, what is the probability your next flight will be on A? b. If your last flight was on B, what is the probability your second next flight will be on A? c. What are the steady-state probabilities? 36. This matrix of transition probabilities deals with brand loyalty to Bark Bits and Canine Chow dog food. Current Purchase Next Purchase Bark Bits Canine Chow Bark Bits 0.75 0.25 Canine Chow 0.20 0.80 a. What are the steady-state probabilities? b. What is the probability that a customer will switch brands on the next purchase after a large number of periods? 37. Bark Bits Company is planning an advertising campaign to raise the brand loyalty of its customers to 0.80. a. The former transition matrix is as follows: What is the new one? b. What are the new steady-state probabilities? c. If each point of market share increases profit by $15,000, what is the most you would pay for the advertising? 38. A city is served by three cable TV companies: Xcellent Cable, Your Cable, and Zephyr Cable. A survey of 1000 cable subscribers shows this breakdown of customers from the beginning to the end of August. Company on August 1 Company on August 31 Xcellent Your Zephyr Xcellent 300 50 50 Your 10 200 40 Zephyr 40 80 230 a. Construct the transition matrix. b. What was each company's market share at the beginning and end of the month? c. If the current trend continues, what will the market shares be? 39. A television ratings company surveys 100 viewers on March 1 and April 1 to find out what is being watched at 6:00 p.m.—the local NBC affiliate's local news, the CBS affiliate's local news, or "Other" which includes all other channels and not watching TV. The results show the following: March 1 Choice Record of Switches During March to Number NBC CBS Other NBC 30 – 5 10 CBS 40 15 – 5 Other 30 5 5 – a. What are the numbers in each choice for April 1? b. What is the transition matrix? c. What ratings percentages do you predict for May 1? 40. Accounts receivable have been grouped into the following states: State 1: Paid State 2: Bad debt State 3: 0–30 days old State 4: 31–60 days old Sixty percent of all new bills are paid before they are 30 days old. The remainder go to state 4. Seventy percent of all 30-day-old bills are paid before they become 60 days old. If not paid, they are permanently classified as bad debts. a. Set up the one-month Markov transition matrix. b. What is the probability that an account in state 3 will be paid? 41. Rent-To-Keep rents household furnishings by the month. At the end of a rental month, a customer can (a) rent the item for another month, (b) buy the item, or (c) return the item. The matrix below describes the month-to-month transition probabilities for the 32-inch stereo televisions the shop stocks. This Month Next Month Rent Buy Return Rent 0.72 0.10 0.18 Buy 0 1 0 Return 0 0 1 What is the probability that a customer who rented a TV this month will eventually buy it? 42. On any particular day, an individual can take one of two routes to work. Route A has a 25% chance of being congested, whereas route B has a 40% chance of being congested. The probability of the individual taking a particular route depends on his previous day's experience. If one day he takes route A and it is not congested, he will take route A again the next day with probability 0.8. If it is congested, he will take route B the next day with probability 0.7. On the other hand, if he takes route B one day and it is not congested, he will take route B again the next day with probability 0.9. Similarly, if route B is congested, he will take route A the next day with probability 0.6. a. Construct the transition matrix for this problem. (Hint: There are four states corresponding to the route taken and the congestion. The transition probabilities are products of the independent probabilities of congestion and next-day choice.) b. What is the long-run proportion of time that route A is taken? 43. Henry, a persistent salesman, calls North's Hardware Store once a week hoping to speak with the store's buying agent, Shirley. If Shirley does not accept Henry's call this week, the probability she will do the same next week is 0.35. On the other hand, if she accepts Henry's call this week, the probability she will not do so next week is 0.20. a. Construct the transition matrix for this problem. b. How many times per year can Henry expect to talk to Shirley? c. What is the probability Shirley will accept Henry's next two calls if she does not accept his call this week? d. What is the probability of Shirley accepting exactly one of Henry's next two calls if she accepts his call this week? 44. The evening television news broadcast that individuals view on one evening is influenced by which broadcast they viewed previously. An executive at network C has determined the following transition probability matrix describing this phenomenon: Current Network News Watched Next Network News Watched A C N A 0.80 0.12 0.08 C 0.08 0.85 0.07 N 0.08 0.09 0.83 a. Which network has the most loyal viewers? b. What are the three networks' long-run market shares? c. Suppose each of the three networks earns $1,250 in daily profit from advertising revenue for each 1,000,000 viewers it has. If, on average, 40,000,000 people watch the evening television news, compute the long-run average daily profit each network generates from its evening news broadcast. 45. Precision Craft, Inc., manufactures ornate pedestal sinks. On any day, the status of a given sink is either: (a) somewhere in the normal manufacturing process, (b) being reworked because of a detected flaw, (c) finished successfully, or (d) scrapped because a flaw could not be corrected. The transition matrix is as follows: Tomorrow's Status Today's Status In-Process Rework Finished Scrapped In-process 0.30 0.15 0.50 0.05 Rework 0.40 0.10 0.30 0.20 Finished 0 0 1 0 Scrapped 0 0 0 1 a. What is the probability of a sink eventually being finished if it is currently in process? b. What is the probability of a sink eventually being scrapped if it is currently in rework? c. What is the probability that a sink currently in rework will have a "finished" status either tomorrow or the next day? (Hint: There are three ways this can happen.) [Show More]

Last updated: 2 years ago

Preview 1 out of 16 pages