True / False
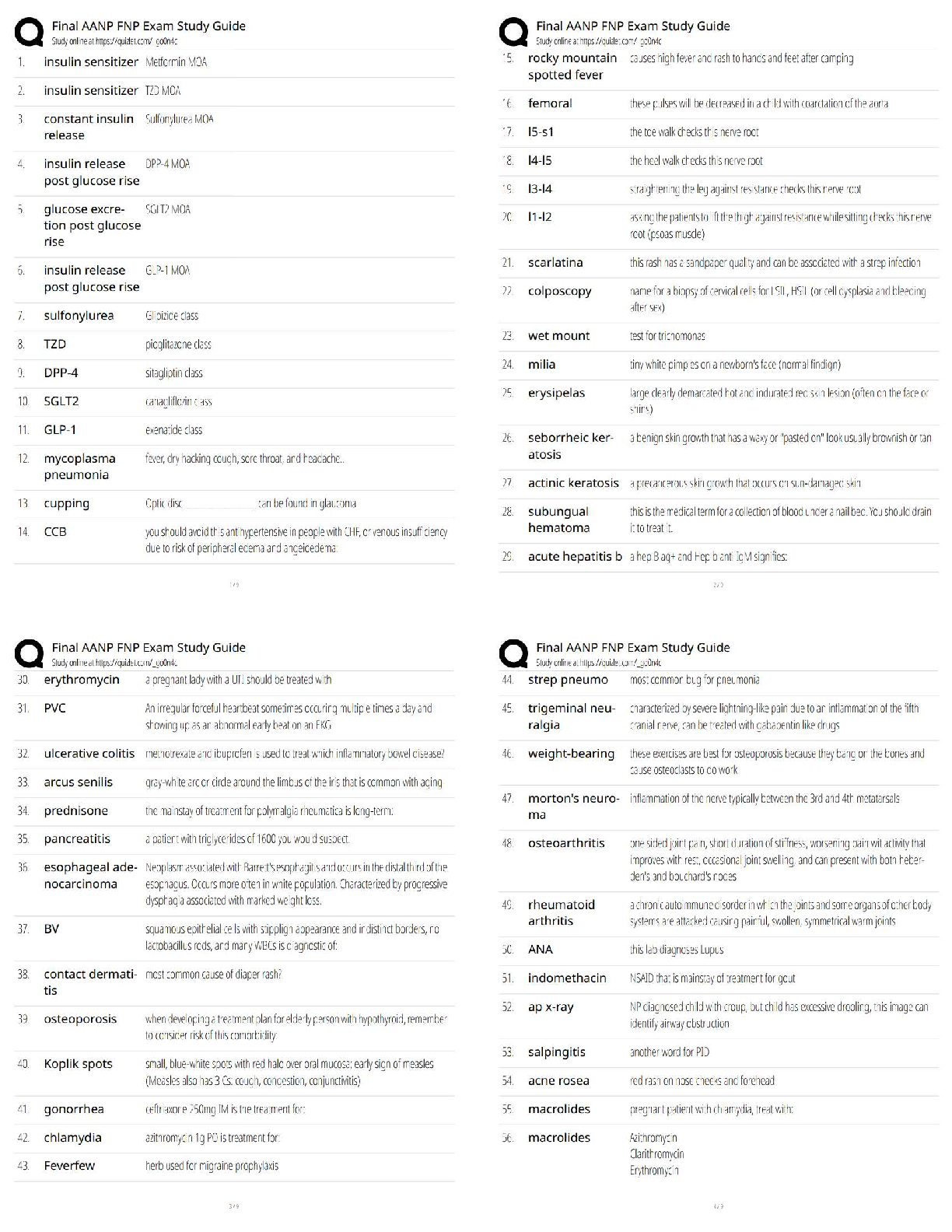
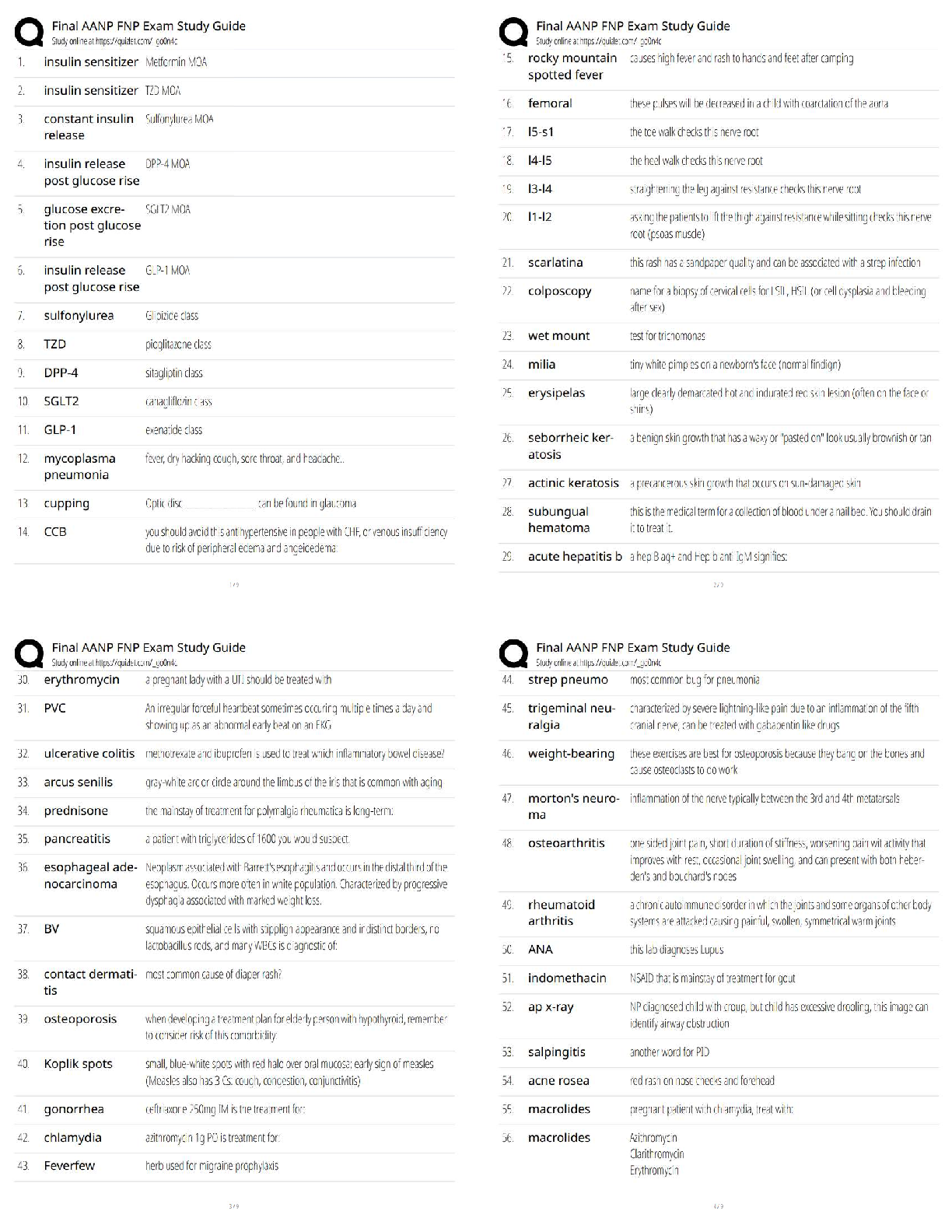
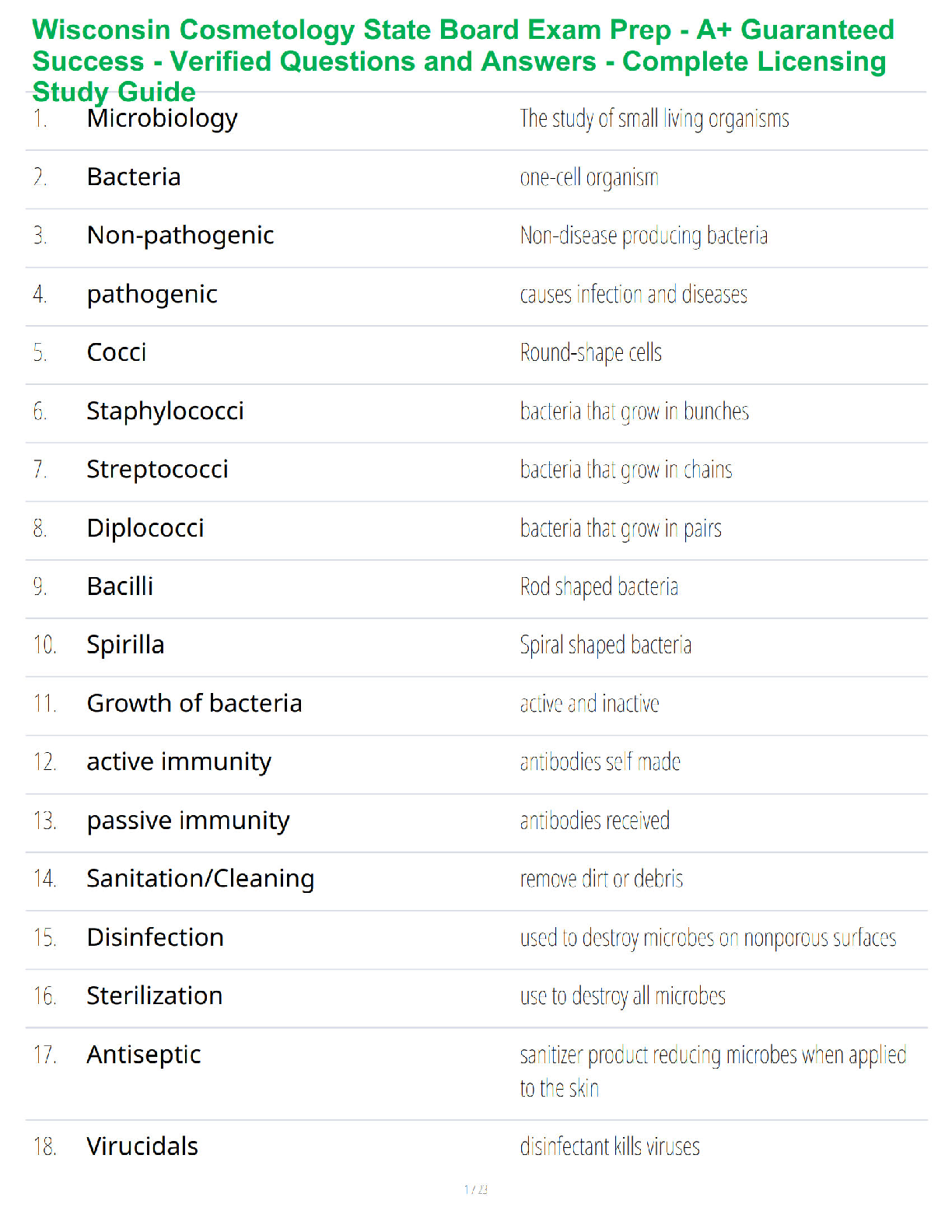
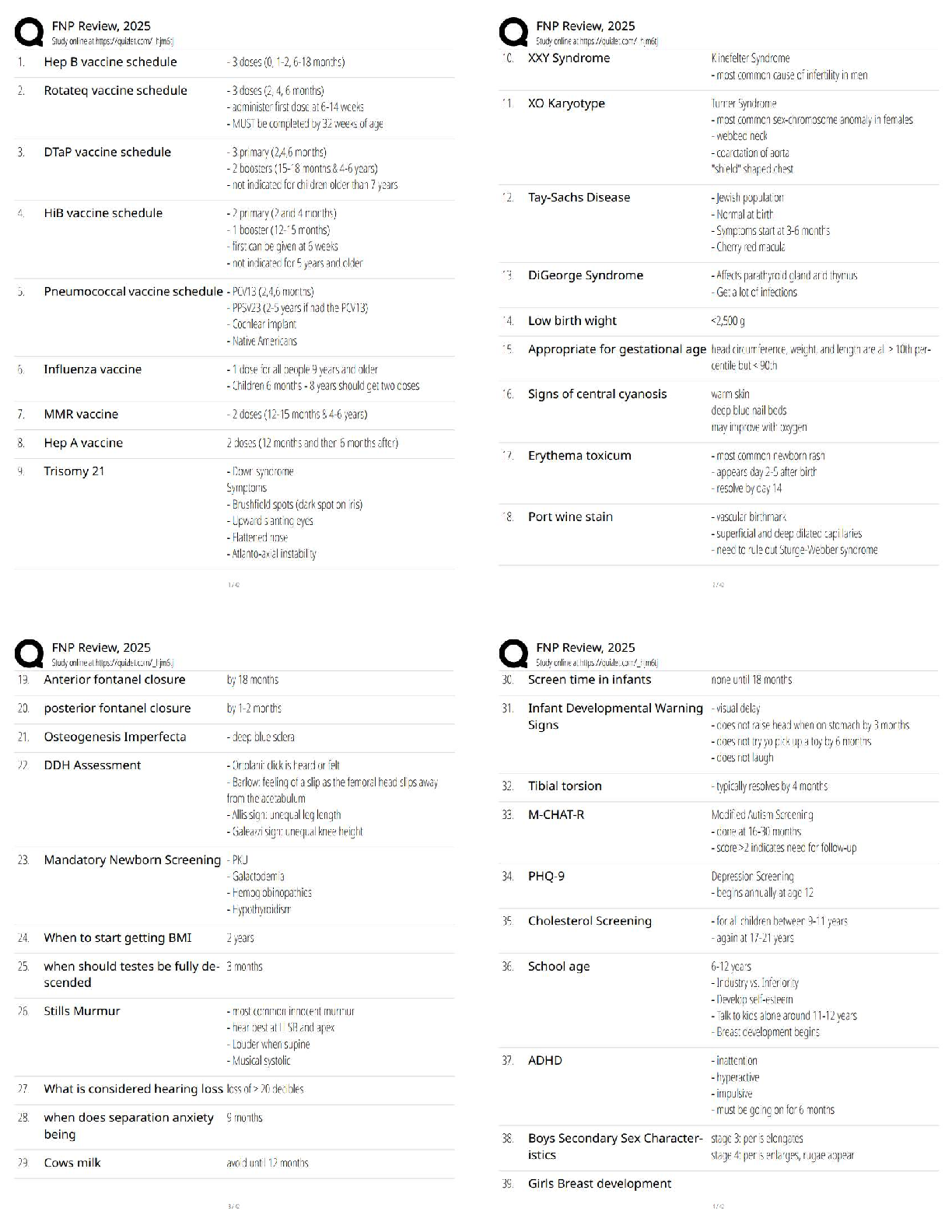
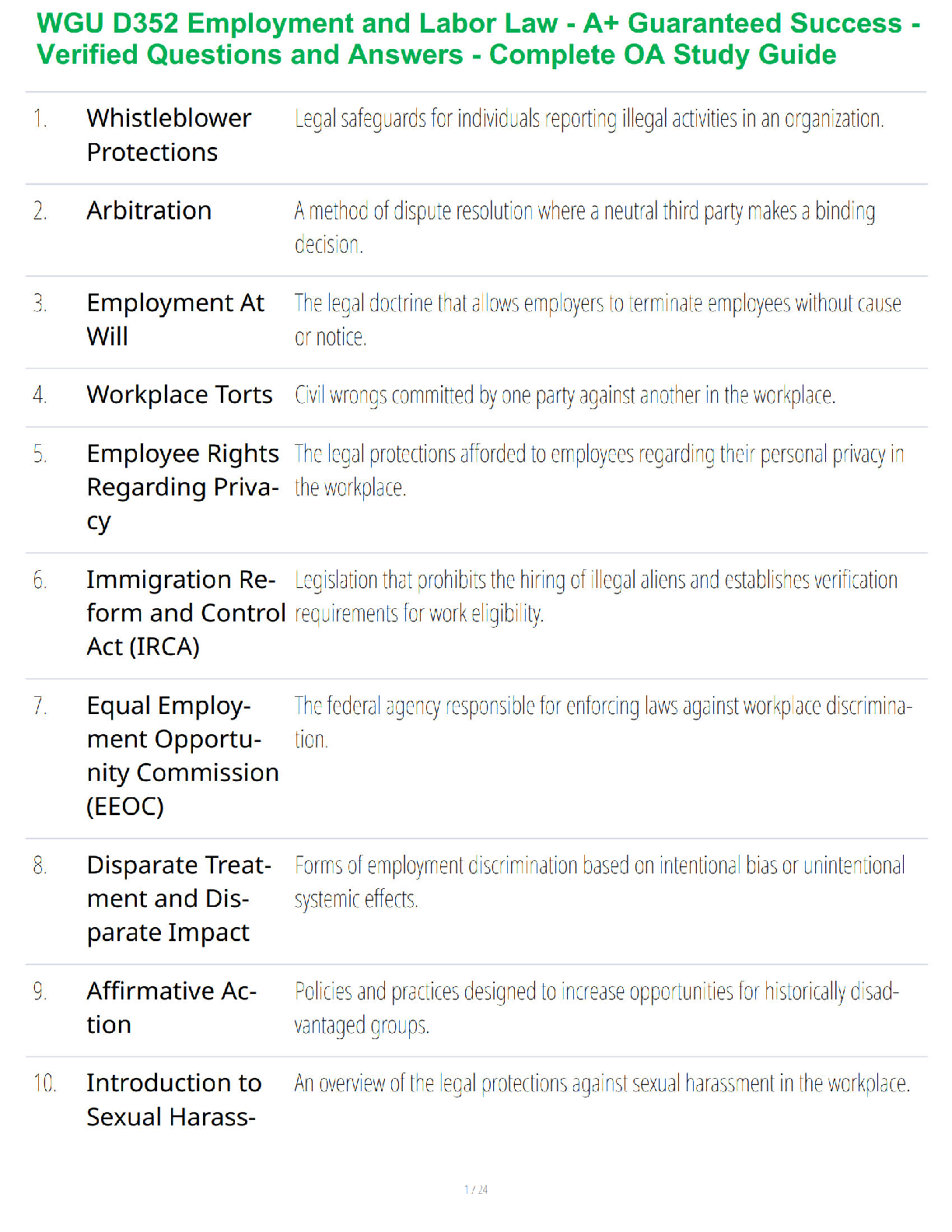
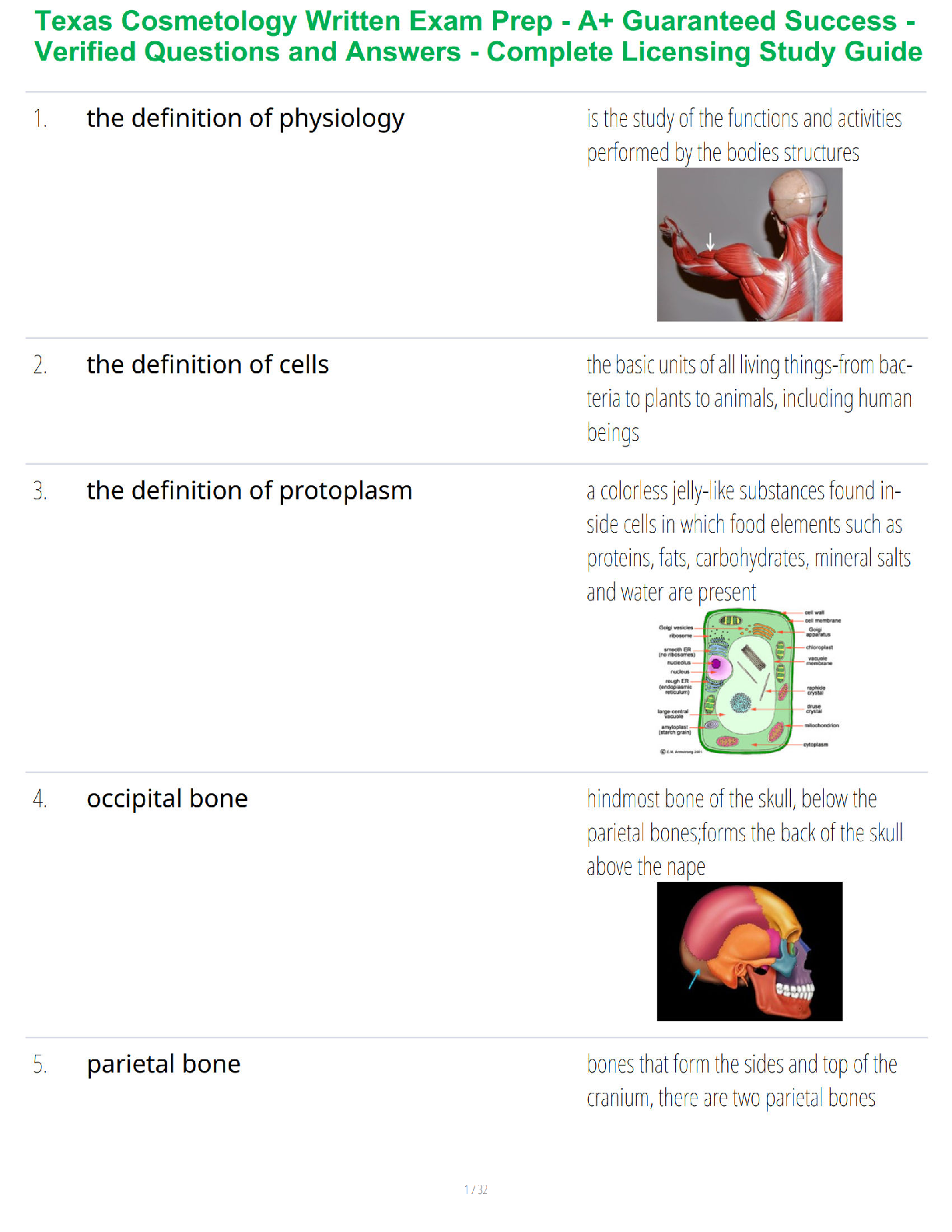
1. Dynamic programming requires that its subproblems be independent of one another.
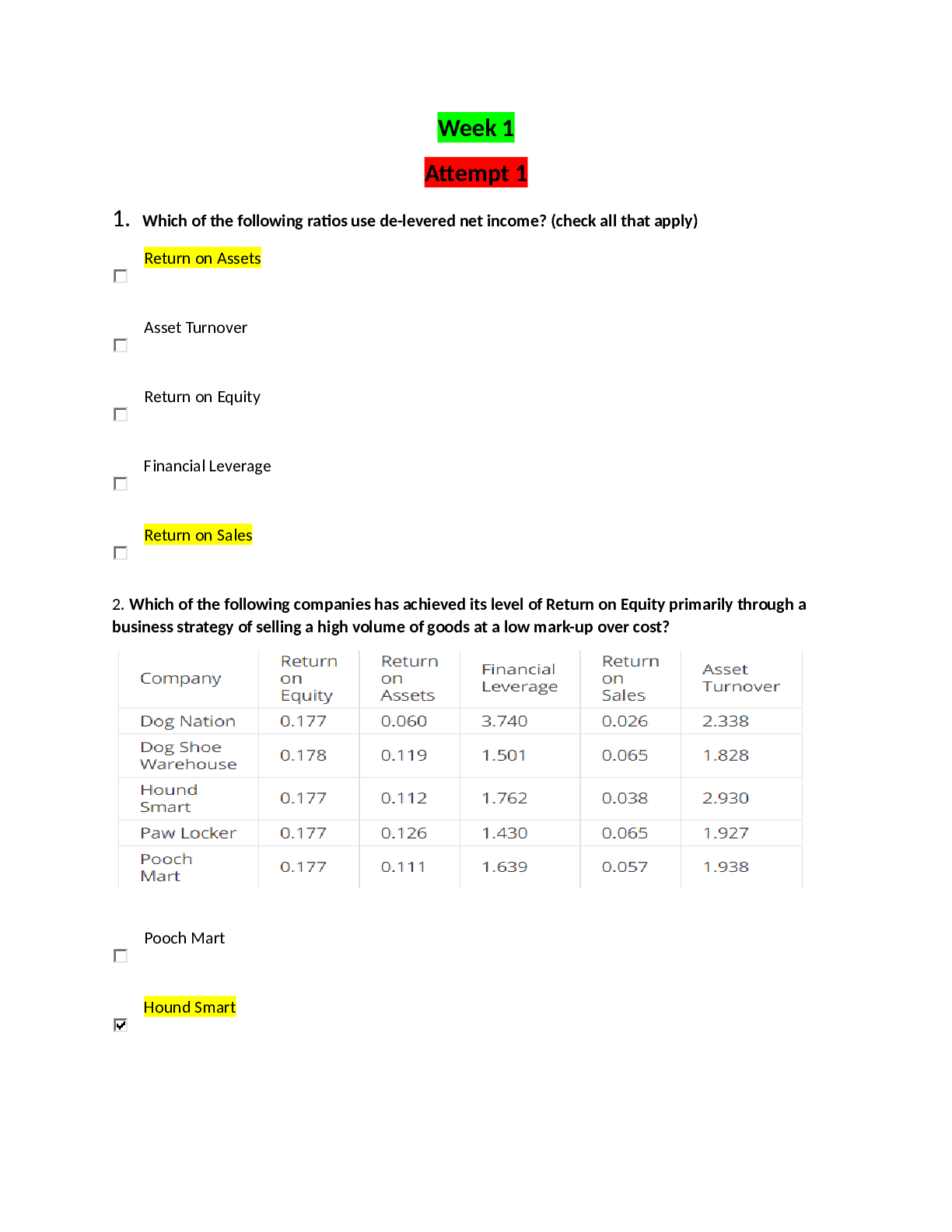
a. True
b. False
2. Dynamic programming, when used for the shortest-route problem, requires complete enum
...
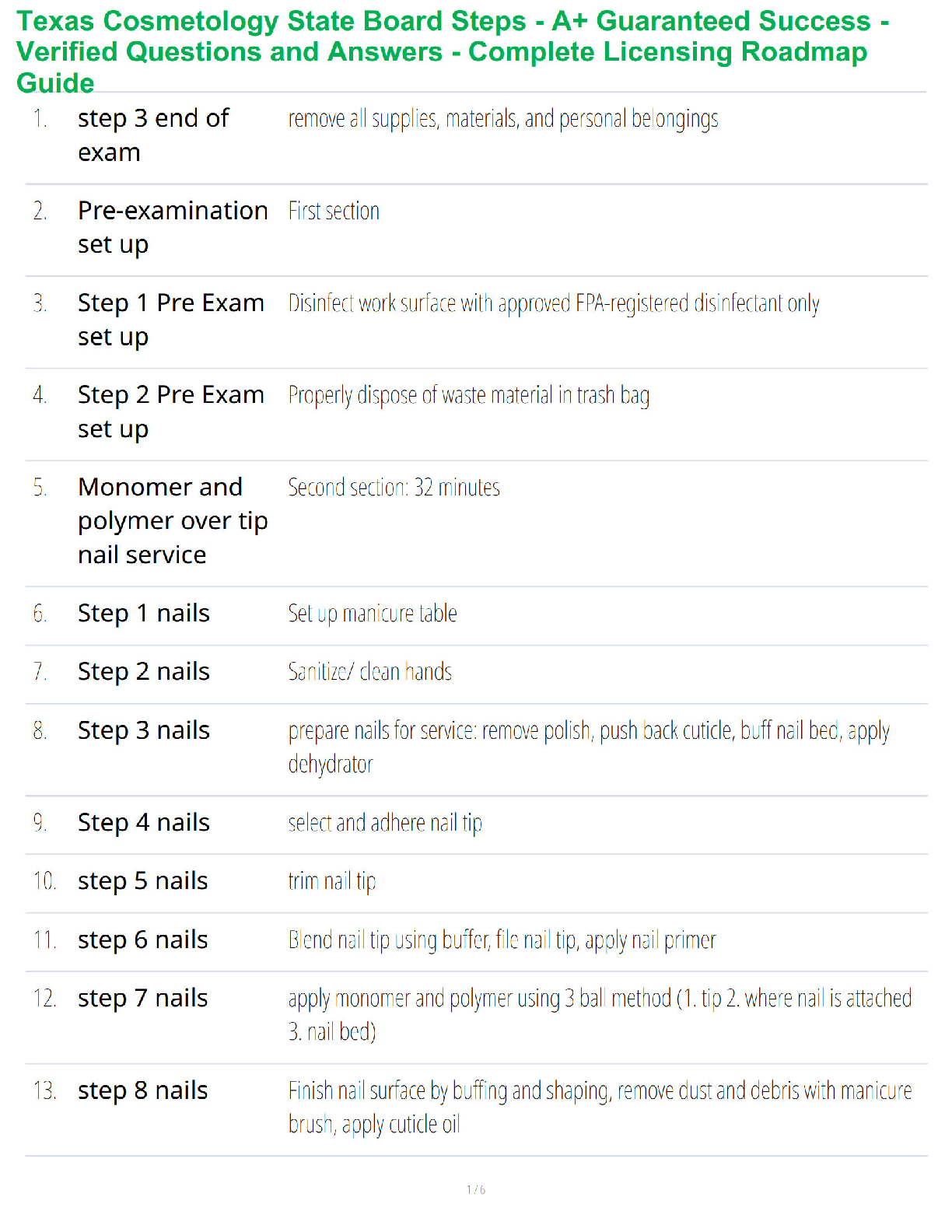
True / False
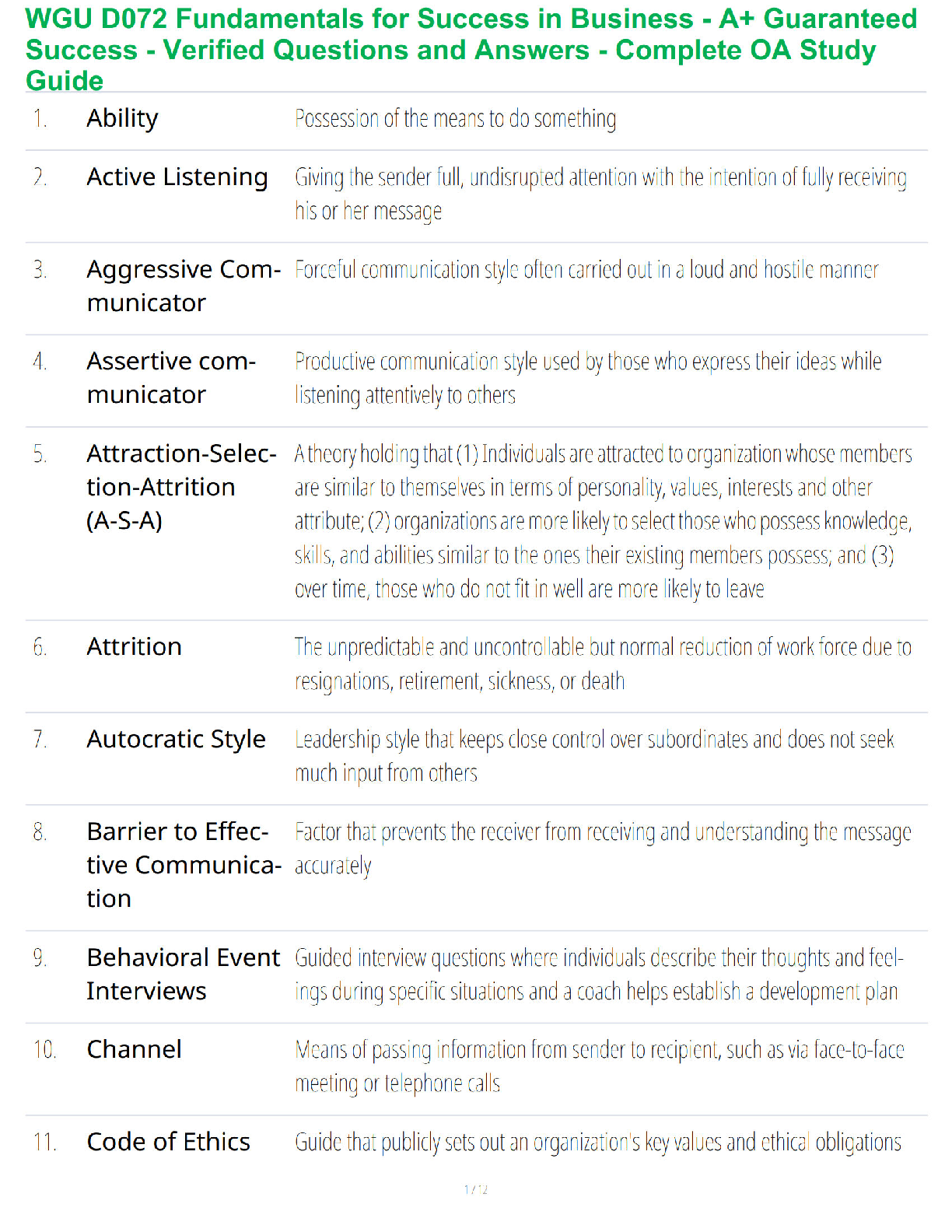
1. Dynamic programming requires that its subproblems be independent of one another.
a. True
b. False
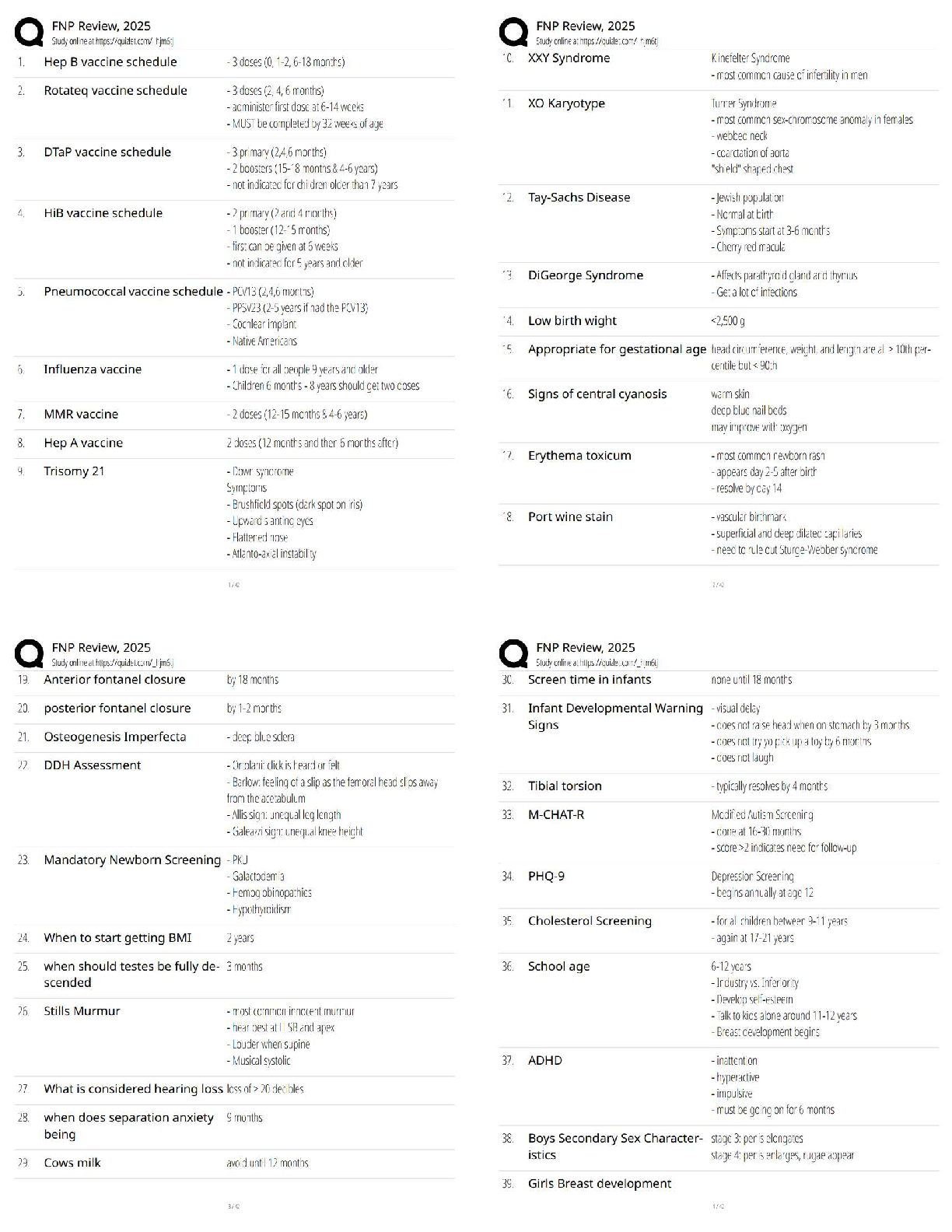
2. Dynamic programming, when used for the shortest-route problem, requires complete enumeration of paths from the beginning to ending node.
a. True
b. False
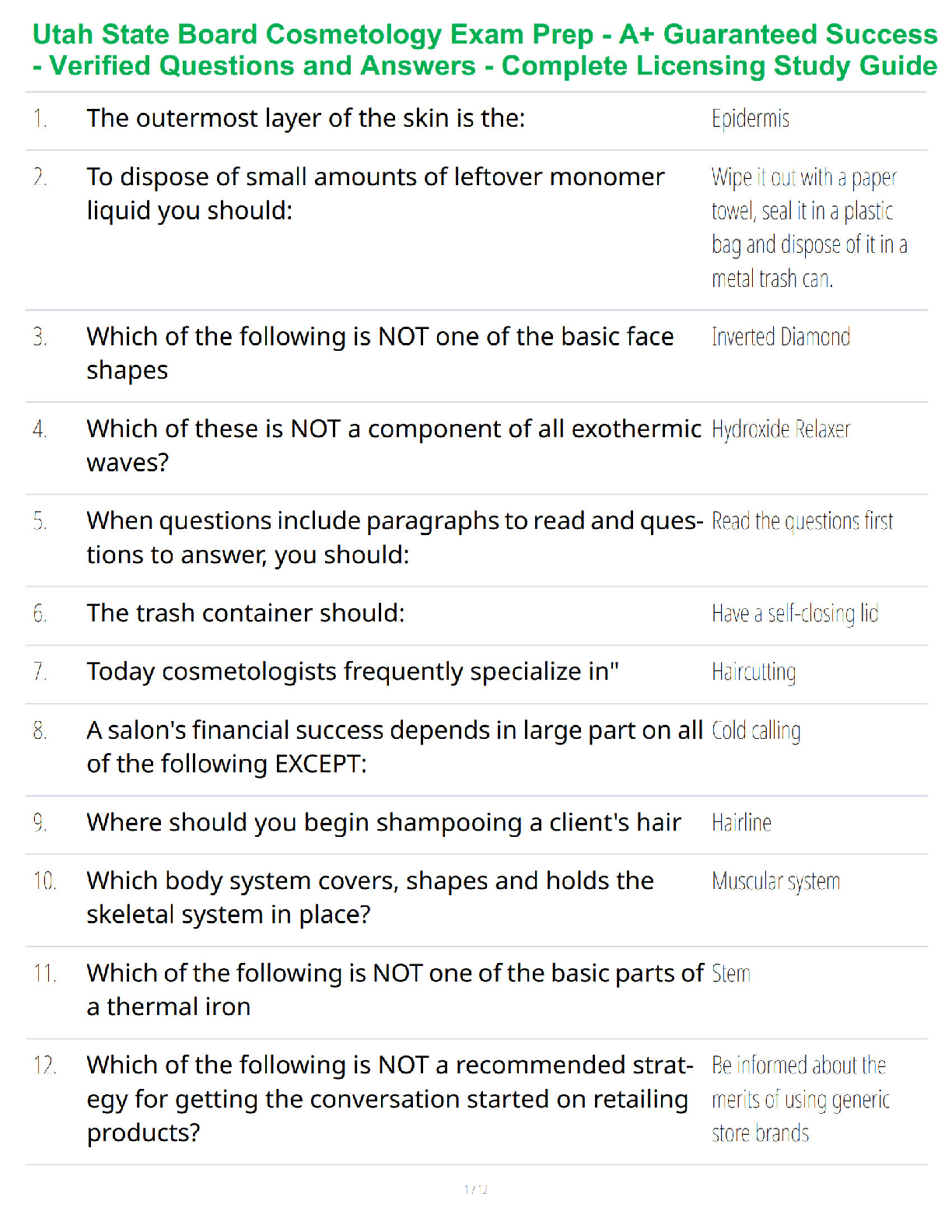
3. The solution of stage k of a dynamic programming problem is dependent upon the solution of stage k−1.
a. True
b. False
4. The output of stage k is the input for stage k−1.
a. True
b. False
5. State variables are a function of a state variable and a decision.
a. True
b. False
6. The return function for a shortest-route problem refers to two directional arcs between nodes.
a. True
b. False
7. In solving a shortest-route problem using dynamic programming, the stages represent how many arcs you are from the terminal node.
a. True
b. False
8. As opposed to a specific technique such as linear programming, dynamic programming is considered a general approach.
a. True
b. False
9. Dynamic programming must only involve a finite number of decision alternatives and a finite number of stages.
a. True
b. False
10. Dynamic programming is a general approach used when it is possible to break a large problem into interrelated smaller problems, with stage decisions proceeding recursively, solving one of the smaller problems at each stage.
a. True
b. False
11. In a production and inventory control problem, the states can correspond to the amount of inventory on hand at the beginning of each period.
a. True
b. False
12. In a knapsack problem, if one adds another item, one must completely resolve the problem in order to find a new optimal solution.
a. True
b. False
13. The subscripts used in dynamic programming notation refer to states.
a. True
b. False
14. In order to use dynamic programming, one must be able to view the problem as a multistage decision problem.
a. True
b. False
15. Finding the optimal solution to each stage of a dynamic programming problem will always lead to an optimal solution to the total problem.
a. True
b. False
16. The stage transformation function identifies which state one reaches at the next stage for a given decision.
a. True
b. False
17. An input state variable and an output state variable together define the condition of the process at the beginning and end of a stage.
a. True
b. False
18. A knapsack problem is so named because the objective is to find the number of N items, each of which has a different weight and value, that can be placed in a knapsack with limited weight capacity so as to maximize the total value of the items placed in the knapsack.
a. True
b. False
Multiple Choice
19. Stages of a dynamic programming solution procedure
a. represent parts of a large mathematical model.
b. often represent a sequence of decisions made over time.
c. are usually not independent of each other.
d. All of these are correct.
20. The stage transformation function
a. transforms the input into the output.
b. transforms a stage into a state.
c. is a different function for each stage.
d. None of these are correct.
21. State variables in a shortest-route problem represent
a. decisions.
b. locations in the network.
c. the minimum distance between nodes.
d. None of these are correct.
22. The function that “transforms” the input of the stage into the output of the stage is referred to as a stage transformation function and
a. is always linear.
b. calculates the return of the transformation.
c. determines the output of the stage.
d. All of these are correct.
23. A return function is a value such as profit or loss associated with making decision dn at
a. stage n for a specific value of output variable xn.
b. stage n for a specific value of input variable xn.
c. stage n for a specific value of stage m.
d. input n for a specific value of output variable xn.
24. If x3 = t4(x4,d4) = x4 − 2d4 and r4(x4,d4) = 16d4, the state variable is
a. t.
b. x.
c. r.
d. d.
25. If x3 = t4(x4,d4) = x4 − 2d4 and r4(x4,d4) = 16d4, the stage transformation function is
a. t.
b. x.
c. r.
d. d.
26. If x3 = t4(x4,d4) = x4 − 2d4 and r4(x4,d4) = 16d4, the subscripts refer to
a. state.
b. stage.
c. transformation.
d. return.
27. The knapsack problem is to determine how many units of each item to place in the knapsack to
a. minimize total value.
b. maximize total value.
c. minimize the number of items in the knapsack.
d. maximize the number of items in the knapsack.
28. Solutions in dynamic programming
a. are not optimal.
b. are unique.
c. represent each stage.
d. All of these are correct.
Subjective Short Answer
29. Find the shortest path through the following network using dynamic programming.
30. Audio Disks will be opening outlets in the greater Phoenix area. The estimated sales at each store are dependent not only on the store location, but also on the number of sales personnel, as presented in the table below ($1000s/year). Each store requires at least two salespeople, and a pool of nine salespeople is available.
Staff Size
2 3 4 5
Store 1 60 85 90 100
Store 2 105 120 130 150
Store 3 120 145 160 175
a. What would the states be in the dynamic programming formulation?
b. Draw the network that represents the dynamic programming formulation.
c.
Given the above network, solve the sales personnel allocation problem by finding the longest path.
31. Consider the following integer linear program:
Max 5x1 + 7x2 + 9x3
s.t. 2x1 + 3x2 + 4x3 ≤ 8
x1 ≤ 3
x2 ≤ 2
x1, x2, x3 ≥ 0, integer
a. Set up the network that represents the dynamic programming formulation.
b. Solve the problem using dynamic programming.
32. A driver wants to make a trip from city 1 to city 7. The road mileage between cities is given below. Find the shortest route.
To City
From City 1 2 3 4 5 6 7
1 − 2 2 4 − − −
2 − − − − 4 10 −
3 − − − − 12 6 −
4 − − − − 10 − −
5 − − − − − − 14
6 − − − − − − 2
7 − − − − − − −
33. The owner of a small construction firm is excavating at three sites. He wishes to assign his five additional trucks in such a way as to minimize his total costs. Each site can use zero to three additional trucks; no site can use more than three trucks efficiently. The following site total costs are known.
Number Cost of Excavating
of Trucks Site 1 Site 2 Site 3
0 $10,000 $15,000 $20,000
1 10,000 14,000 18,000
2 9,200 13,250 17,500
3 8,500 12,750 17,250
a.
Use dynamic programming to find the assignment of the additional trucks that minimizes total cost.
b.
If the owner had only four trucks to assign, what would be the optimal assignment and total cost?
34. A number of types of items are to be shipped as cargo. The total available weight in the truck is 10 tons. Determine the number of units of items to be shipped to maximize profit.
Item Weight (tons) Profit ($1000s)
A 3 5
B 4 7
C 2 3
35. A cargo company has a set of delivery patterns for its goods from its location at city 1 to a series of cities 2, 3, 4, 5, and 6. The delivery times between cities are given in hours below. Find the shortest route.
To City:
From City: 1 2 3 4 5 6 7
1 − 6 10 7 − − −
2 6 − 4 − 5 − −
3 10 4 − 4 2 4 −
4 7 − 5 − − 8 −
5 − 5 3 − − − 7
6 − − 4 8 − − 5
7 − − − − 7 5 −
36. Unidyne Corporation is currently planning the production of red dye number 56 for the next four months. Production and handling costs, as well as production and storage capacity, vary from month to month. These data are given in the table below.
Production and holding costs are in $1000s per batch, and production levels and storage capacities are in batches. Holding costs are based on inventory on hand at the end of the month. The number of orders for batches the sales department has received over the four-month period is also given.
Month Production Cost Maximum Production Holding Cost Storage Capacity Orders Received
February 11 3 3 4 2
March 15 4 2 3 4
April 16 3 2 5 2
May 9 2 1 2 3
Unidyne does not wish to have any inventory of the dye at the end of May. Its current inventory is two batches. Determine a production schedule for the next four months.
37. Marvelous Marvin is planning his annual "Almost Everything Must Go" inventory clearance sale. Marvin has decided to allocate 18 shelf feet to the cooking section. He is considering offering up to five items for sale in this category.
Item Shelf Feet Required Expected Profit
A 1 $ 10
B 2 25
C 3 40
D 5 70
E 7 100
If Marvin wants at least one item A and one item B on sale, what stock should he have on sale, and what is the total expected profit?
38. Franklin Plate Company manufactures commemorative plates for holidays. The company is currently planning its production schedule for this year's Thanksgiving plate.
Discussions with the sales manager have indicated that sales of the plate will run from August through November. The production manager has determined the manufacturing cost per plate for each of these months as well as the sales demand (in 1000s) and manufacturing capacity (in 1000s). The data are as follows:
Month
Demand Manufacturing Cost per Plate Maximum Production
August 2 2 6
September 4 3 6
October 6 3 4
November 3 4 3
The maximum inventory level possible at the end of any month is 5000 plates. The storage cost per plate for each plate in inventory at the end of the month is $0.50.
Franklin has no inventory on hand at the beginning of August and wishes to have no inventory left after November. Use dynamic programming to determine an optimal production schedule.
39. Walt's Custom Boats manufactures luxury yachts. Walt is phasing out production of his 42-foot Sportfisher that he plans to replace with a 44-foot Sportfisher. Walt currently has orders for the next four months for the 42-foot model after which he will cease production. The following data (with costs in $1000s) are for the next four months:
Month Production Cost per Boat Maximum Production Level Holding Cost per Boat in Inventory at End of Month Maximum Storage Capacity Number of Boats to Be Delivered in Month
May 25 4 1 6 1
June 27 3 1 5 3
July 30 2 2 3 3
August 29 3 1 4 4
If Walt's current inventory of 42-foot Sportfishers is one boat, how should Walt schedule production of the 42-foot Sportfisher over the next four months to minimize the total production and inventory holding costs?
40. Mission Bay Development Corporation is developing an exclusive 25-acre parcel of property. It has received bids from five builders to purchase construction lots. Because of the different nature of the builders, they desire different sized lots. The data are as follows:
Builder Lot Size
Requested Offered Price
per Lot Maximum Number of
Lots Desired
1 3 acre $ 50,000 6
2 1 acre 15,000 5
3 6 acre 105,000 8
4 20 acre 350,000 1
5 5 acre 91,000 2
How should Mission Bay sell the land to maximize total sales revenue?
41. In the following shortest-route problem, travel is only permitted from left to right. Use dynamic programming to determine the shortest path from node 1 to:
a. node 15.
b. node 14.
[Show More]
















.png)
.png)
.png)