Questions and Answers > COMPUTER S 1245 CS_GRE Questions and Answers in Computer Science. CONTAINS 70 Q&A

Document Content and Description Below

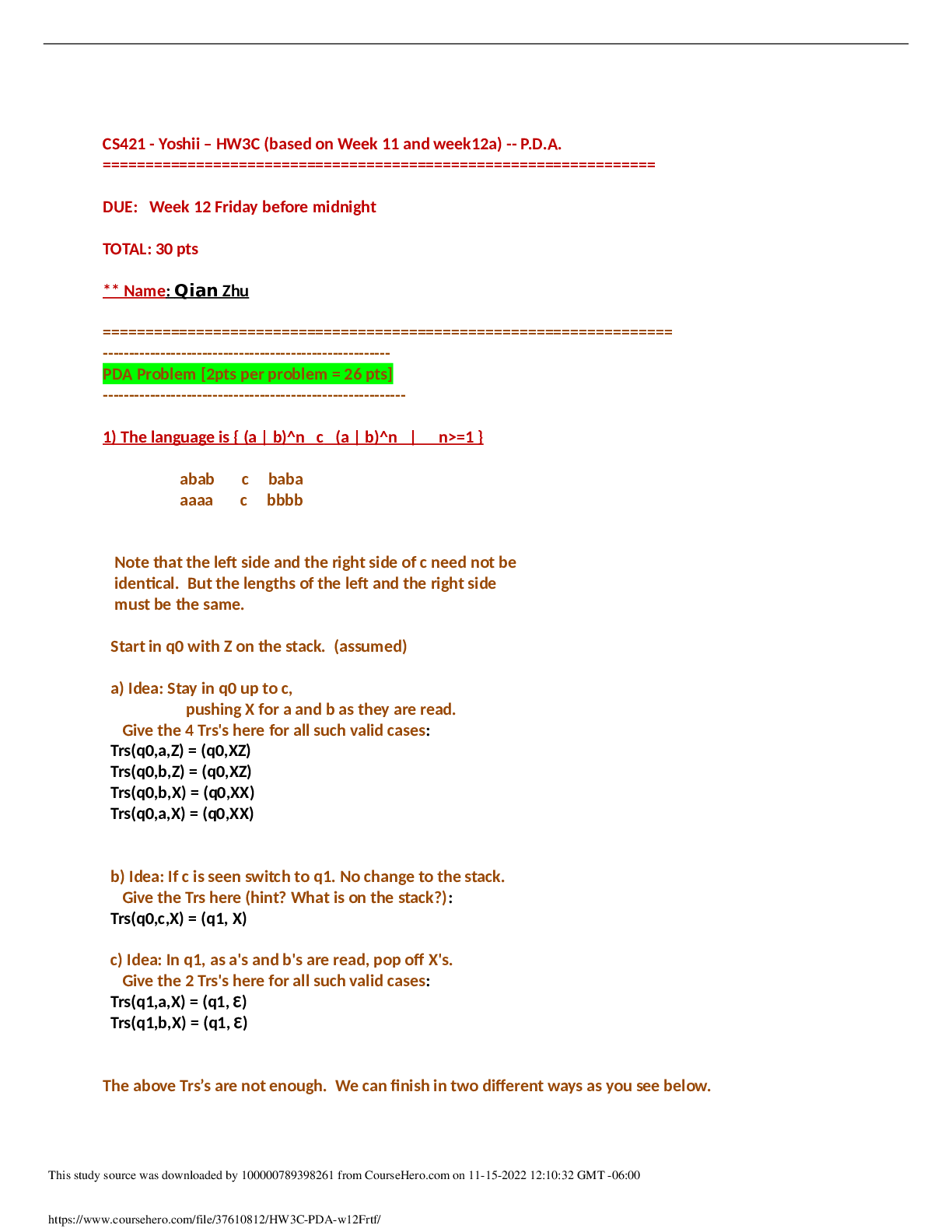
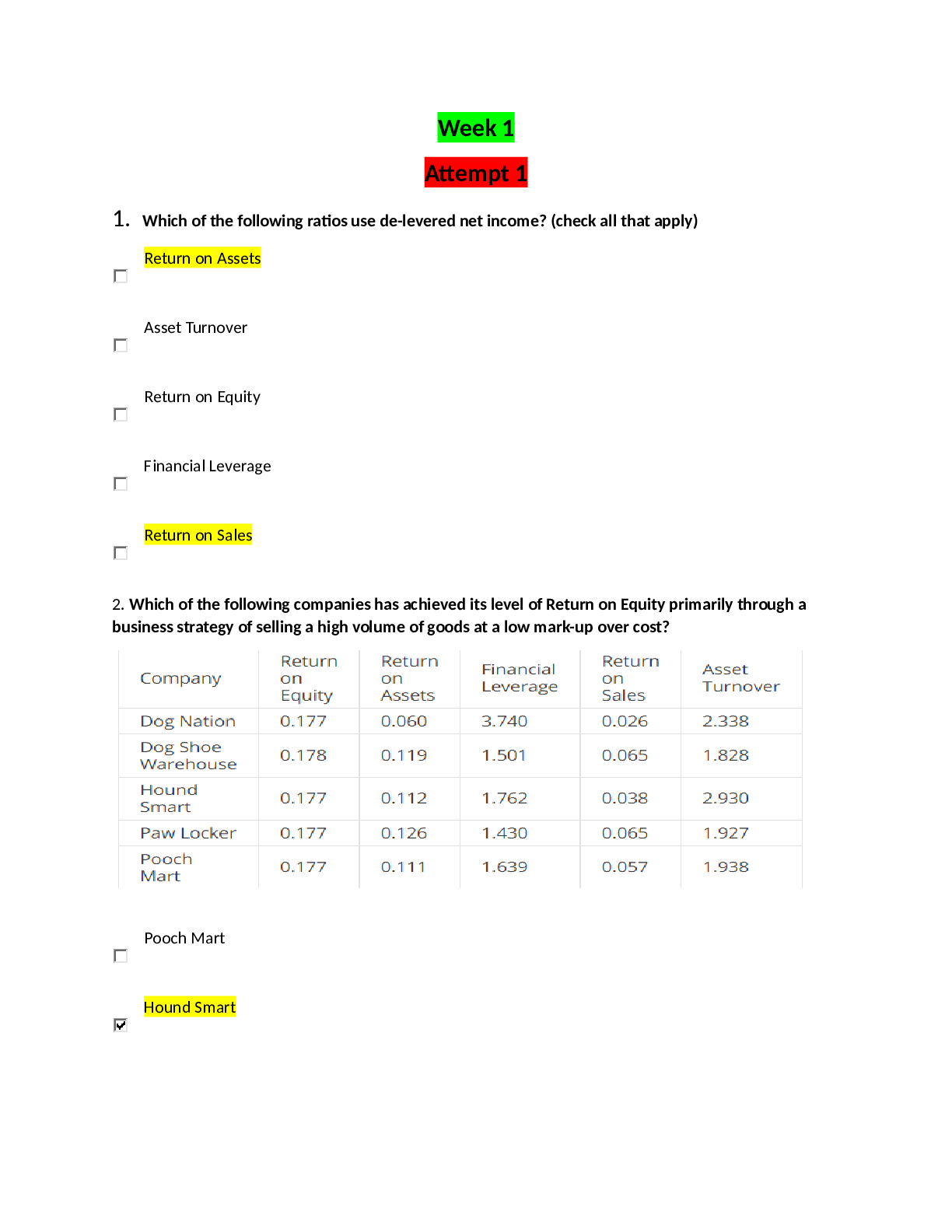
COMPUTER S 1245 CS_GRE Questions and Answers in Computer Science The Questions in this material are collected from Computer Science Subject Graduate Record Examination Preparation Materials The... solutions are explicitly personal and are primarily intended for discussion purposes with people who want to share ideas Neither correctness nor completeness is assumed or implied Do not rely on it Your feedbacks are most welcome! SAMPLE QUESTIONS Question 1. Any set of Boolean operators that is su–cient to represent all Boolean expressions is said to be complete. Which of the following is NOT complete? A. fAND, NOTg B. fNOT, ORg C. fAND, ORg D. fNANDg E. fNORg Solution 1. Recall that the basics of Boolean algebra operators are AND, OR and NOT. These three operators are needed to express any Boolean algebra. So we need to check which of the above alternative sets fails to express these operators. To that end, recall that using AND and NOT, we can express OR, using De’Moivre Theorem, as A OR B = A AND B. Similarly, using OR and NOT, we can express AND as A AND B = A OR B. Moreover, NAND can express NOT as the NAND of a boolean variable with itself. Since NAND is negation of AND, it follows that NAND can express AND by simply inverting the result of NAND (i.e. given A and B, A AND B = Negation(A NAND B) = (A NAND B) NAND (A NAND B)). Since it can express AND and NOT, it follows that it can express OR. A similar argument can be applied to NOR. NOR expresses NOT as the NOR of a variable with itself. It follows that it can express OR as the NOR of a result of NOR with itself. Finally De’Moivre’s Theorem yields the expression to express AND using NOR (i.e. NOT and OR). With AND and OR, we can’t express NOT in anyway. Thus the answer is C. Question 2. Which of the following decimal numbers has an exact representation in binary notation? A. 0.1 B. 0.2 C. 0.3 D. 0.4 E. 0.5 Solution 2. 1 The only thing we need to remember here is on how to convert decimal numbers to binary. ˆIn order to convert integer decimal numbers to binary, divide the number by 2, note the remainder and continue the same operation with the quotient until a quotient of 0 is obtained at which step we need to stop. All the remainders are then written starting from the last to the flrst resulting the required binary expression. ˆIn order to convert a fraction part, as is the case in this question, multiply the fraction by 2, note the integer part of the product, and continue the same operation with the fraction part of the product until a product of 1.0 is obtained. The required binary fraction is then 0:i1i2i3::: where the i’s are the integer parts of the products starting from the flrst to the last (if the operation stops at some stage). Apply this rule to 0.1 to get the following products 0.2, 0.4, 0.8, 1.6, (take away 1 and continue with 0.6), 1.2, 0.2, ... Stop! We had already encountered 0.2 which means we will encounter it again and again if we continue which means this operation will go indeflnitely. Thus all the choices A, B, C and D do not have flnite (exact) binary notation because all the decimal numbers 0.1, 0.2, 0.3 (which will be 0.6 on the second stage) and 0.4 are encountered in the conversion procedure for 0.1 which did not terminate. The only choice left is E; indeed 0.5 will give 1.0 in the second stage which is the terminating stage resulting the binary 0.1 as its binary representation. Hence the answer is choice E. Question 3. Bob writes down a number between 1 and 1,000. Mary must identify that number by asking "yes/no" questions to Bob. Mary knows that Bob always tells the truth. If Mary uses an optimal strategy, then she will determine the answer at the end of exactly how many questions in the worst case? A. 1,000 B. 999 C. 500 D. 32 E. 10 Solution 3. The di–cult part on this question is to understand what sort of questions Mary should ask Bob. If she asks questions like ‘Is it the number 764?’, ‘Is it the number 342?’, etc, then surely Mary will need to ask 999 questions in the worst case in order to get the answer. 2 The optimal strategy is to ask questions like ‘Is it GREATER THAN 500?’, ‘Is it GREATER THAN 250?’, etc; each time throwing away half of the interval and working with the remaining half. This is simply binary search method and Mary will need to ask a maximum of log2(1000) questions. Hence the answer is choice E. Question 4. If x is a string then xR denotes the reversal of x. If x and y are strings, then (xy)R = A. xyR B. yxR C. yRx D. xRyR E. yRxR Solution 4. The answer can easily be verifled to be choice E. [It is similar to transposing a product two matrices which is the product of the transposes in reverse order.] Question 5. A procedure that printed the binary tree AQQ · ·Bee % % D E CJ›J›F in postorder would produce as output1 A. ABCDEF B. ABDECF C. DBEAFC D. DEBFCA E. DEFBCA 1Please note that in this tree diagram and the subsequent tree diagrams, some EDGES are drawn with no actual nodes. This is due to the fact that, according to the package I am using to draw trees (parsetree.sty), if one wants to have only one child node, then the node is drawn as middle child (neither right child not left one). So in order to clarify that indeed the child node is either left or right, I am adding additional empty redundant edge. Such edges should be treated as NON-EXISTENT. 3 Solution 5. Just remember that † Inorder traverses a tree from Left to Root and then to Right. † Preorder traverses a tree from Root to Left and then to Right. † Postorder traverses a tree from Left to Right and then to Root. All these traversals start at the root node of the tree and perform the operation on each node of the tree recursively. Thus choices A and E refer to nothing, choice B is a result of preorder traversal, choice C is a result of inorder traversal, and choice D is a result of postorder traversal. Hence the answer is choice D. Question 6. Which of the following is not a binary search tree? A. 5 ,,ll 3SS ¶ ¶ 2 4 7 B. 5 ##cc 3TT ••2 7TT ••6 C. 5 %%ee 4\\ ¿¿3TT ••2 D. 5 ,,ll 4TT ••3 6TT • • 7 E. 5 ,,ll 4SS ¶ ¶ 3 6 7 Solution 6. A binary search tree is a binary tree such that for all the nodes in the tree, we have all left children are less than the root which is less than or equal to all the right children. Such trees are used for searching in logarithmic scale time. The answer is choice E. Question 7. Consider the following Pascal-like program fragment. var i, j : integer; procedure P(k, m : integer); begin k := k - m; m := k + m; k := m - k; end 4 i := 2; j := 3; P(i, j); If both parameters to P are passed by reference, what are the values of i and j at the end of the program fragment? A. i = 0; j = 2 B. i = 1; j = 5 C. i = 2; j = 3 D. i = 3; j = 2 E. None of the above Solution 7. When parameters, to functions or procedures, pass by reference or pointer (also referred to as by name), the changes made in the function or procedure are reflected in the caller. When parameters pass by value, the change is not reflected. Thus when i and j go with the values 2 and 3 respectively, k and m will get these values in that order and then k will have the value 2 - 3 = -1, m will have a value -1 + 3 = 2, and flnally k will have a value 2 - -1 = 3. These values are sent back to i and j resulting i = 3 and j = 2. Hence the answer is D. **Observe that the procedure swaps the values of i and j with out using any extra memory. BUT it is very wrong to use such a function in applications which deal with big absolute value numbers. As such suppose that i is assigned the largest positive integer value possible of the programming language under consideration and let j be assigned any negative integer, then the flrst line in the function will assign k a value above the integer limit resulting to a wrong result! Question 8. A starvation-free job-scheduling policy guarantees that no job waits indeflnitely for service. Which of the following job-scheduling policies is starvation-free? A. Round-robin B. Priority queuing C. Shortest job flrst D. Youngest job flrst E. None of the above Solution 8. Consider Priority queuing; a policy where the process with the highest priority is executed flrst irrespective of its arrival. Under such policy, suppose a system is currently executing a process and is in the middle of execution when a process with higher priority arrives. This means the system will suspend the execution of the process which was already executing and will start executing this new process. If this new process needs some resources which are already occupied by the former process then a deadlock occurs as neither the higher priority process will complete execution 5 without these resources nor the old process can proceed executing in order to release resources for the new process. Thus there can be a deadlock (·starvation). The same argument applies for shortest job flrst policy in which case a shortest process might need resources that are occupied by longer processes which were already in the middle of their execution. Youngest process flrst policy is where the process that arrived last will execute flrst which again can have starvation. The Round-robin policy which is preemptive scheduling algorithm forces a process if it seems it is holding resource which are required by others thus avoiding starvation. Thus the answer is A. Question 9. Consider a singly linked list of the form where F is a pointer to the flrst element in the linked list and L is a pointer to the last element in the list. The time of which of the following operations depends on the length of the list? A. Delete the last element of the list B. Delete the flrst element of the list C. Add an element after the last element of the list D. Add an element before the flrst element of the list E. Interchange the flrst two elements of the list Solution 9. Remember that after performing any operation, the structure of the list must remain intact; in other words F and L must point to the flrst and last elements respectively. Choice B needs only the operation F = F->next; Choice C needs only the operations L->next = new node, L = new node; Choice D needs only the operations new node->next = F, F = new node; Choice E needs only the operations T=F, F=F->next, T->next=F->next, F->next=T; All these do not depend on the length of the list. The answer is therefore A. Indeed in order to delete the last element from the list, we need to flrst locate the element before the last (which can not be accessed from L). Thus we must parse all the list from the flrst till the element just before the last after which we can delete the last element and assign L to the one before. Question 10. p := 1; k := 0; while k < n do begin p := 2 * p; 6 k := k + 1; end; For the program fragment above involving integers p, k, and n, which of the following is a loop invariant; i.e., true at the beginning of each execution of the loop and at the completion of the loop? A. p = k + 1 B. p = (k + 1)2 C. p = (k + 1)2k D. p = 2k E. p = 2k+1 Solution 10. Choice E is incorrect even before the loop started hence it is out. When one loop is done, the value of p is 2 and that of k is 1. At this time, we see that both choices B and C are incorrect and thus they are out. Performing one more loop gives p a value 4 and k will have a value 2 at which time choice A becomes incorrect. Hence the answer is choice D. Question 11. Consider an output-producing, deterministic flnite automaton (DFA) of the kind indicated in the flgure below, in which it is assumed that every state is a flnal state. Assume that the input is at least four bits long. Which of the following is (are) true? I. The last bit of the output depends on the start state. II. If the input ends with \1100", then the output must end with \1". III. The output can not end with \1" unless the input ends with \1100". A. I only B. II only C. I and II only D. II and III only E. I, II, and III Solution 11. 7 We start our analysis of the DFA by points II and III. First of all note that a label a=b on an edge denotes that with an input a, we do transition along the edge and produce an output b. Now, if the input ends with \1100", then we can verify, by starting from any of the states, that the last output bit is always a ‘1’. Hence point II is true. To analyze III we proceed as follows. Denote the states (circles in the diagram) by A; B; C; and D starting from the bottom left and going in the clockwise direction. In order to get an output ‘1’ as the last output bit, the last transition must be from state A to state B which is equivalent to say the last input bit was a ‘0’. We can get to state A only from state D which means the second from the last output bit is a ‘0’ and the second from the last input was a ‘0’ too. To get to state D, either we must have come from state D itself or from state C. This means, in any case the third from the last output was a ‘0’ and the third from the last input was a ’1’. If we had come to state D from itself, then the fourth, from the last, output bit was a ‘0’ and the fourth, from the last, input bit was a ‘1’; if on the other hand we had come from state C then we must had come to state C either from state A or from state B in which in any case gives the fourth, from the last, output bit was a ‘0’ and the fourth from the last input bit as a ‘1’. Thus we conclude that in order to get a ‘1’ as the last bit of the output, we must have the last four bits of the input to be \1100". Hence III is true. By II and III, we conclude that I is incorrect. Hence the answer is choice D. Question 12. A particular BNF deflnition for a \word" is given by the following rules. <word> ::= <letter> | <letter><pairlet> | <letter><pairdig> <pairlet> ::= <letter><letter> | <pairlet><letter><letter> <pairdig> ::= <digit><digit> | <pairdig><digit><digit> <letter> ::= a | b | c | ... | y | | z <digit> ::= 0 | 1 | 2 | ... | 9 Which of the following lexical entries can be derived from < word >? I. word II. words III. c22 A. None B. I and II only C. I and III only D. II and III only E. I, II, and III Solution 12. Observe that both < letter > and < digit > produce only a single character, both < pairlet > and < pairdig > produce even number of characters; hence < word > produces odd number of characters. Thus I is automatically incorrect. II can be produced with the following chain of rules: <word> = <letter><pairlet> 8 = <letter><pairlet><letter><letter> = <letter><letter><letter><letter><letter> = words and III can be produced with the following chain of rules: <word> = <letter><pairdig> = <letter><digit><digit> = c22 Hence the answer is choice D. Question 13. Consider the following C-like program. #include <stdio.h> main() { float sum = 0.0, j = 1.0, i = 2.0; while (i/j > 0.001) { j = j + j; sum = sum + i/j; printf("%f\n", sum); } } How many lines of output does the program produce? A. 0 - 9 B. 10 - 19 C. 20 - 29 D. 30 - 39 E. More than 39 Solution 13. Since there is one line of output for each loop, we need to determine the number of times the loop executes. Since i is constant, we need to see the growth of j only. Let the initial value of j be denoted by J1 and the subsequent values by Jn for n= 2, 3, ... so that J denotes a progression of j. We see that Jn = 2Jn¡1; J1 = 2, which gives Jn = 2n¡1; n = 1, 2, ... The loop will execute as long as i=j = 2:0=2n¡1 > 0:001 which gives n < 3log210 + 2 or n < 11:97 Thus the loop will execute 11 times which is equivalent to say there will be 11 lines of output. Hence the answer is choice B. Question 14. For the C-like code shown above, which of the following is the integer that best approximates the last number printed? A. 0 9 B. 1 C. 2 D. 3 E. 4 Solution 14. We need the value of sum at the last loop execution which is 0 + 1 + 1 2 + ... + 2048 2 = 1.999 Thus the answer is choice C. Question 15. An integer c is a common divisor of two integers x and y if and only if c is a divisor of x and c is a divisor of y. Which of the following sets of integers could possibly be the set of all common divisors of two integers? A. f¡6; ¡2; ¡1; 1; 2; 6g B. f¡6; ¡2; ¡1; 0; 1; 2; 6g C. f¡6; ¡3; ¡2; ¡1; 1; 2; 3; 6g D. f¡6; ¡3; ¡2; ¡1; 0; 1; 2; 3; 6g E. f¡6; ¡4; ¡3; ¡2; ¡1; 1; 2; 3; 4; 6g Solution 15. Since 0 can not divide any number, we see that choices B and D are out of question. If an integer a is among common divisors of two integers, then surely all divisors of a must also be in the set of common divisors; thus choice A is incorrect since 3 must also be in the set. If both 3 and 4 are among common divisors, then so should be 3 * 4 = 12 by Euclid’s lemma (* if we let the two integers x and y, then since 4jx, we must have x = 4q for some integer q and thus 3j4q with gcf(3,4)= 1 =) 3jq =) q = 3p for some integer p and thus x = 4q = 4⁄3⁄p = 12p =) 12jx. Similar argument for y.) Thus choice E is incorrect and the correct answer is choice C [Show More]

Last updated: 2 years ago

Preview 1 out of 47 pages