University of Houston, Downtown - MGT 3332 Chapter 18. Contains 81 Questions with the answers provided at the end.

Document Content and Description Below

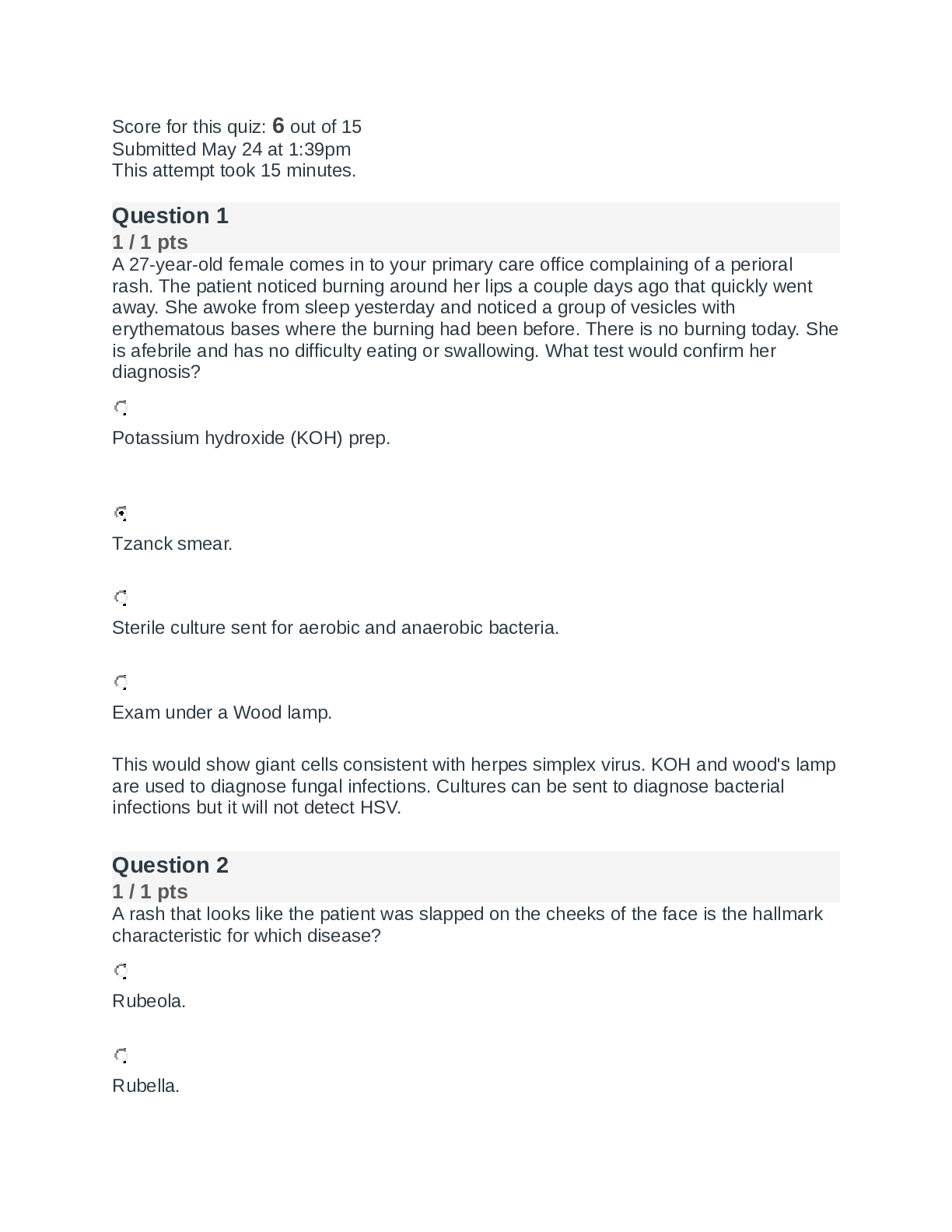
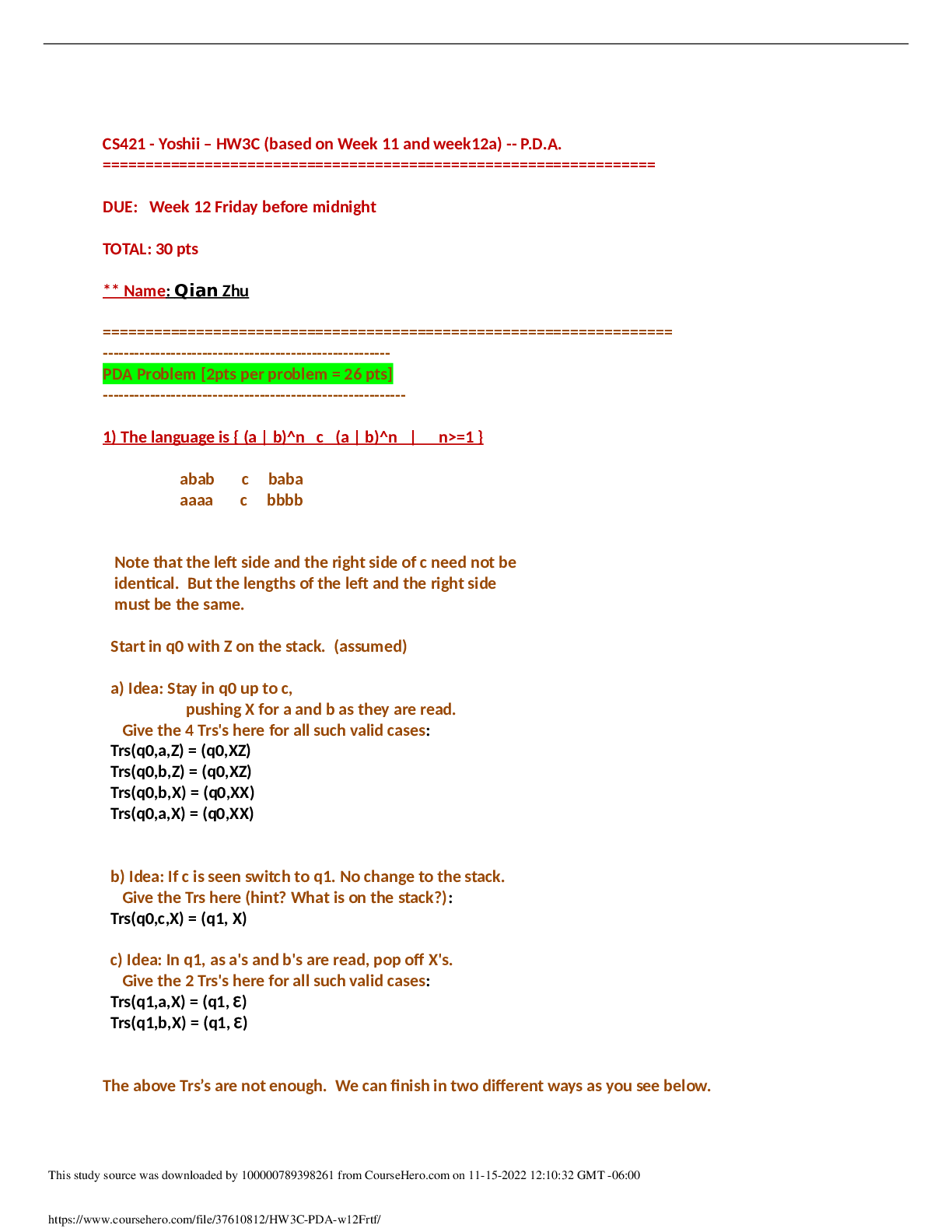
18 Student: ___________________________________________________________________________ 1. Waiting lines occur even in underloaded systems because of variability in service rates and/or arrival rat... es. True False 2. A system has one service facility that can service 10 customers per hour. The customers arrive at a variable rate, which averages six per hour. Since there is excess capacity, no waiting lines will form. True False 3. The goal of waiting-line management is to eliminate customer waiting lines. True False 4. The cost of customer waiting is easy to estimate, the number waiting multiplied by the wait cost per minute. True False 5. In a theme park like Disney world, reservation systems are a win-lose situation since only those holding reservations are satisfied. True False 6. The point that minimizes total queuing system costs is that point where waiting costs and capacity costs are equal. True False 7. A multiple-channel system assumes that each server will have its own waiting line, and line changing is not permitted. True False 8. A dental office with two professionals (one dentist, one hygienist) who work together as a team would be an example of a multiple-channel system. True False 9. A single-server, variable-service-time system is known as an M/D/1 system. True False 10. The most commonly used queuing models assume that the arrival rate can be described by a Poisson distribution. True False 11. The goal of queuing analysis is to balance the cost of providing a level of service capacity with the possible loss of business due to customers leaving the line or refusing to wait. True False 12. According to Little's law, the number of people in line depends on the time of day that they arrive. True False 13. For a system that has a low utilization ratio, decreasing service capacity slightly will have only negligible effect on customer waiting time. True False 14. An approach to reducing the variability in processing times might include greater standardization. True False 15. The queuing models discussed in the text apply only to steady-state conditions. Steady state exists only when customers arrive at a steady rate; that is, without any variability. True False 16. In an infinite-source model, the average number being served is equal to the ratio of the arrival rate to the service rate. True False 17. In an infinite-source model, the average time in line is equal to the average number in line divided by the arrival rate. True False 18. In an infinite-source model, the system utilization is the ratio of the arrival rate to the service capacity. True False 19. To reduce the average number waiting in line, it is important to increase utilization. True False 20. All infinite-source queuing models require the system utilization to be less than 1.0. True False 21. Queue discipline requires a security presence to maintain order. True False 22. Compared to a single-channel system with exponential service time, a single-channel system with a constant service time causes a reduction of 50 percent in the average number waiting in line. True False 23. To reduce waiting times by actively managing system constraints, managers could consider: (I) using temporary workers. (II) shifting demand from high-demand periods to low-demand periods. (III) offering more service variety. (IV) discovering bottlenecks. A. I and III only B. I, II, and IV only C. III only D. II and IV only E. IV only 24. The value of standardizing some or all of a service is demonstrated by the shorter wait times observed in models with: A. constant demand rates. B. finite queues. C. infinite sources. D. finite sources. E. constant service times. 25. Which of the following would tend to increase the difference between the actual time customers spent waiting and the perceived time spent waiting by those customers? (I) Lots of experience with the service on the part of customers (II) Anxiety on the part of customers (III) A pleasant physical environment for the customers A. I and II only B. I only C. II only D. III only E. I, II, and III 26. In which of these settings would one be least likely to encounter first-come service? A. a fast-food restaurant B. a doctor's office C. a hotel check-in operation D. an emergency room E. a check-out line 27. A customer growing frustrated with the wait and leaving the facility (without being served) is an example of: A. reneging. B. utilizing. C. balking. D. jockeying. E. departing. 28. Although it is generally the case that service systems have enough capacity, waiting lines result when __________ exceeds capacity for periods of time. A. homogeneity B. variability C. price D. demand E. heterogeneity 29. Why is there waiting in an infinite-source queuing system? A. poor scheduling of servers B. slow service C. low utilization D. variability in arrival and service rates E. multiple-phase processing 30. The goal of queuing analysis is to minimize: A. the sum of customer waiting costs and capacity costs. B. the sum of customer waiting time and service time. C. capacity costs. D. customer waiting time. E. idle servers. 31. A basic difference between infinite-source and finite-source queuing models is the: A. number of servers. B. average waiting time. C. arrival distribution. D. size of potential calling population. E. processing rate. 32. If a manager increases system utilization (assuming no change in the customer arrival rate) what happens to the customer waiting time? A. It increases exponentially. B. It increases proportionally. C. It decreases proportionally. D. It decreases exponentially. E. No change. 33. A single-phase queuing system is one which has a single: A. channel. B. server. C. customer being served. D. operation. E. waiting line. 34. A single-channel queuing system has an average service time of eight minutes and an average time between arrivals of 10 minutes. The arrival rate is: A. 6 per hour. B. 7.5 per hour. C. 8 per hour. D. 10 per hour. E. 12.5 per hour. 35. In a _______ system, customers enter the waiting line, receive service, and leave. A. fast-track B. simulated C. queuing D. random E. nonrandom 36. Which of the following is not generally considered to be a measure of system performance in a queuing analysis? A. the average number waiting in line B. the average number in the system C. system utilization D. the cost of servers plus customer waiting cost E. average serving time 37. The total cost curve: A. starts at zero and increases as service capacity increases. B. begins high and decreases as service capacity increases. C. starts high, declines, then increases again. D. remains relatively flat regardless of service capacity. E. starts at zero, increases rapidly, then declines slowly back to zero. 38. Little's law states that the number of people in a waiting line is the average customer arrival rate multiplied by the: A. average time in the system. B. average waiting time. C. service time minus the waiting time. D. average number in line. E. waiting time. 39. As the ratio of arrival rate to service rate is increased, which of the following is likely? A. Customers move through the system in less time because utilization is increased. B. Customers move through the system more slowly because utilization is increased. C. Utilization is decreased because of the added strain on the system. D. The average number in the system decreases. E. There really is no change since arrival rates are offset by service rates. 40. Servers and channels are described with many acronyms except: A. M/P/S. B. M/M/1. C. M/D/1. D. M/M/S. 41. A single-bay car wash with a Poisson arrival rate and an exponential service time has cars arriving an average of 10 minutes apart, and an average service time of four minutes. The system utilization is: A. .24. B. .40. C. .67. D. 2.50. E. 1.25. 42. A multiple-channel queuing system with a Poisson arrival rate and exponential service time has an average arrival rate of four customers per hour and an average service time of 18 minutes per customer. The minimum number of servers required to avoid an overloaded system is: A. 1. B. 2. C. 3. D. 4. E. 5. 43. Which one of the following measures of system performance is a key measure with respect to customer satisfaction? A. average number of customers waiting in line B. system utilization C. average number of customers in the calling population D. probability of a server being busy E. capacity costs per hour 44. A single-channel queuing system has an average service time of 16 minutes per customer, which is exponentially distributed. The manager is thinking of converting to a system with a constant service time of 16 minutes. The arrival rate will remain the same. The effect will be to: A. increase utilization. B. decrease utilization. C. increase the average waiting time. D. decrease the average waiting time. E. not have any effect since the service time is unchanged. 45. When the waiting cost incurred by customers likely varies, an appropriate queuing model is: A. single channel, single phase. B. single channel, multiple phase. C. multiple channel, single priority. D. multiple channel, multiple phase. E. multiple channel, multiple priority. 46. A ________ is one way of reducing perceived waiting time. A. bonus B. gatekeeper C. reservation D. diversion E. number calling system 47. An alternative strategy to increase the capacity of a service system is: A. reducing the number of arrivals. B. increasing variability. C. increasing the processing rate. D. reducing the number of servers. E. reducing the processing rate. 48. A queuing system has four crews with three members each. The number of "servers" is: A. 3. B. 4. C. 7. D. 12. E. 1. 49. A multiple-channel system has customers arriving at an average rate of five per hour and an average service time of 40 minutes. The minimum number of servers for this system to be underloaded is: A. 2. B. 3. C. 4. D. 5. E. 6. 50. If a firm has reached the point at which further reducing waiting time is not economically feasible, reducing the ______________ is sometimes attractive. A. channels B. perceived service time C. capacity underload D. perceived waiting time E. system underutilization 51. A bank of 10 machines requires regular periodic service. Machine running time and service time are both exponential. Machines run for an average of 44 minutes between service requirements, and service time averages six minutes per machine. What is the probability that a machine will have to wait for service with two operators? A. .654 B. .090 C. .346 D. .910 E. .016 52. A bank of 10 machines requires regular periodic service. Machine running time and service time are both exponential. Machines run for an average of 44 minutes between service requirements, and service time averages six minutes per machine. What is the average machine downtime with two operators? A. 1.71 minutes B. 3.46 minutes C. 6.25 minutes D. 7.71 minutes E. 9.46 minutes 53. A bank of 10 machines requires regular periodic service. Machine running time and service time are both exponential. Machines run for an average of 44 minutes between service requirements, and service time averages six minutes per machine. What is the average number of machines down when there is one operator? A. 1.49 B. 3.35 C. 4.40 D. 6.65 E. 8.51 54. A bank of 10 machines requires regular periodic service. Machine running time and service time are both exponential. Machines run for an average of 44 minutes between service requirements, and service time averages six minutes per machine. If operators cost $15 per hour in wages and fringe benefits and machine downtime costs $75 per hour in lost production, what is the optimal number of operators for this bank of machines? A. 1 B. 2 C. 3 D. 4 E. 5 55. A bank is designing a new branch office and needs to determine how much driveway space to allow for cars waiting for drive-up teller service. The drive-up service will have three tellers and a single waiting line. At another branch of the bank in a similar setting, the average service time for drive-up tellers is four minutes per customer, and average arrival rate is 36 customers per hour. It is expected that the new bank will have similar characteristics. How many spaces should be provided to have a 96 percent probability of accommodating all of the waiting cars? A. 10 B. 11 C. 12 D. 13 E. 14 56. A restaurant at a popular Colorado casino provides priority service to player's card holders. The restaurant has 10 tables or booths where customers may be seated. The service time (time a booth or table is occupied) averages 40 minutes once a party is seated. The customer arrival rate is 12 parties per hour, with the parties being equally divided between card holders and people without player's cards. What is the average time that player's card holders wait to be seated? A. approx. 4 minutes B. approx. 8 minutes C. approx. 12 minutes D. approx. 15 minutes E. approx. 2 minutes 57. A restaurant at a popular Colorado casino provides priority service to player's card holders. The restaurant has 10 tables or booths where customers may be seated. The service time (time a booth or table is occupied) averages 40 minutes once a party is seated. The customer arrival rate is 12 parties per hour, with the parties being equally divided between card holders and people without player's cards. What is the average time that parties without player's cards wait to be seated? A. approx. 4 minutes B. approx. 8 minutes C. approx. 12 minutes D. approx. 15 minutes E. approx. 2 minutes 58. A restaurant at a popular Colorado casino provides priority service to player's card holders. The restaurant has 10 tables or booths where customers may be seated. The service time (time a booth or table is occupied) averages 40 minutes once a party is seated. The customer arrival rate is 12 parties per hour, with the parties being equally divided between card holders and people without player's cards. On average, how many parties with player's cards are waiting to be seated? A. 0.52 B. 0.41 C. 0.88 D. 1.23 E. 1.75 59. A restaurant at a popular Colorado casino provides priority service to player's card holders. The restaurant has 10 tables or booths where customers may be seated. The service time (time a booth or table is occupied) averages 40 minutes once a party is seated. The customer arrival rate is 12 parties per hour, with the parties being equally divided between card holders and people without player's cards. On average, how many parties without player's cards are waiting to be seated? A. 0.52 B. 0.41 C. 0.88 D. 1.23 E. 1.75 60. A restaurant at a popular Colorado casino provides priority service to player's card holders. The restaurant has 10 tables or booths where customers may be seated. The service time (time a booth or table is occupied) averages 40 minutes once a party is seated. The customer arrival rate is 12 parties per hour, with the parties being equally divided between card holders and people without player's cards. On average, how much longer do parties without player's cards spend in the system, compared to parties with the player's cards? A. 2 minutes B. 4 minutes C. 8 minutes D. 10 minutes E. It is impossible to say without more information. 61. Offering an "early bird" special at a restaurant to reduce waiting times during peak hours is an example of: A. demand shifting. B. queuing psychology. C. service phasing. D. service standardization. E. outsourcing. 62. A restaurant that implements a limited menu and a "no substitutions" policy during peak dining hours is practicing _____________ with respect to waiting-line management. A. demand shifting B. queuing psychology C. service standardization D. service phasing E. outsourcing 63. Which of the following would reduce perceived waiting times most dramatically in a doctor's office? A. putting all clocks out of sight B. removing couches C. having the patient fill out forms D. implementing a "no-cell-phone" policy E. keeping expected waiting times from the patients 64. In a multichannel system with multiple waiting lines, customers shifting among the waiting lines is an example of: A. departing. B. utilizing. C. abandoning. D. balking. E. jockeying. 65. Customers arrive at a suburban ticket outlet at the rate of 14 per hour on Monday mornings. This can be described by a Poisson distribution. Selling the tickets and providing general information takes an average of three minutes per customer, and varies exponentially. There is one ticket agent on duty on Mondays. Determine each of the following: (A) system utilization (B) average number in line (C) average time in line (D) average time in the system 66. During the early morning hours, customers arrive at a branch post office at an average rate of 45 per hour (Poisson), while clerks can handle transactions in an average time (exponential) of four minutes each. Find: (A) the average number of customers waiting for service if six clerks are used. (B) the minimum number of clerks needed to keep the average time in the system to under five minutes. (C) If clerk cost is $30 per hour and customer waiting time represents a "cost" of $20 per hour, how many clerks can be justified on a cost basis? 67. Customers filter into a record shop at an average of one per minute (Poisson) where the service rate is 15 per hour (Poisson). Determine the following: (A) the average number of customers in the system with eight servers (B) the minimum number of servers needed to keep the average time in the system to under six minutes 68. A department has five semiautomatic pieces of equipment which operate for an average of 79 minutes before they must be reloaded. The reloading operation takes an average of 21 minutes per machine. Assume exponential distributions. What is the minimum number of servers needed to keep the average downtime per cycle to less than 25 minutes? 69. Two troubleshooters handle service calls for 10 machines. The average time between service requirements is 18 days, and service time averages two days. Assume exponential distributions. While running, each machine can produce 1,500 pieces per day. Determine: (A) the percentage of time troubleshooters are idle. (B) each machine's net productivity. (C) If troubleshooters represent a cost of $150 per day, and machine downtime cost is $600 per day, would another troubleshooter be justified? Explain. 70. A department has five machines that each run for an average of 8.4 hours (exponential) before service is required. Service time average is 1.6 hours (exponential). (A) While running, each machine can produce 120 pieces per hour. With one server, what is the average hourly output actually achieved? (B) With two servers, what is the probability that a machine would be served immediately when it requires service? (C) If machine downtime cost is $100 per hour per machine, and server time costs $30 per hour, how many servers would be optimal? 71. Customers arrive at a video rental desk at the rate of one per minute (Poisson). Each server can handle .40 customers per minute (Poisson). (A) If there are four servers, determine: (1) The average time it takes to rent a video (2) The probability of three or fewer customers in the system (B) What is the minimum number of servers needed to achieve an average time in the system of less than three minutes? 72. Consider these data regarding the multiple-server, priority service queuing model: Service Rate: 2 per hour (Poisson) Number of Servers: 5 What is the overall average arrival rate? 73. Consider these data regarding the multiple-server, priority service queuing model: Service Rate: 2 per hour (Poisson) Number of Servers: 5 What is system utilization? 74. Consider these data regarding the multiple-server, priority service queuing model: Service Rate: 2 per hour (Poisson) Number of Servers: 5 What is the average time in line for a high-priority item? 75. Consider these data regarding the multiple-server, priority service queuing model: Service Rate: 2 per hour (Poisson) Number of Servers: 5 What is the average time in line for a low priority item? 76. Consider these data regarding the multiple-server, priority service queuing model: Service Rate: 2 per hour (Poisson) Number of Servers: 5 What is the average time in the system for a high-priority item? 77. Consider these data regarding the multiple-server, priority service queuing model: Service Rate: 2 per hour (Poisson) Number of Servers: 5 What is the average time in the system for a low-priority item? 78. Consider these data regarding the multiple-server, priority service queuing model: Service Rate: 2 per hour (Poisson) Number of Servers: 5 What is the average number of high-priority items waiting in line for service? 79. Consider these data regarding the multiple-server, priority service queuing model: Service Rate: 2 per hour (Poisson) Number of Servers: 5 What is the average number of low-priority items waiting in line for service? 80. Consider these data regarding the multiple-server, priority service queuing model: Service Rate: 2 per hour (Poisson) Number of Servers: 5 What is the average number of all items waiting in line for service? 81. A manager assembled the following information about an infinite-source waiting line system: five servers, an arrival rate of six per hour, and a service time of 20 minutes. The manager has determined that the average number of customers waiting for service is .04. Determine each of the following: (A) the system utilization (B) the average waiting time in line in minutes (C) the average time in the system (D) the average number in the system 18 Summary Category # of Questions AACSB: Analytic 32 AACSB: Reflective Thinking 49 Accessibility: Keyboard Navigation 64 Blooms: Apply 32 Blooms: Remember 41 Blooms: Understand 8 Learning Objective: 18-01 What imbalance does the existence of a waiting line reveal? 1 Learning Objective: 18-02 What causes waiting lines to form; and why is it impossible to eliminate them completely? 17 Learning Objective: 18-03 What metrics are used to help managers analyze waiting lines? 51 Learning Objective: 18-04 What very important lesson does the constant service time model provide for managers? 10 Learning Objective: 18- 05 What are some psychological approaches to managing waiting lines; and why might a manager want to use them? 2 Level of Difficulty: 1 Easy 13 Level of Difficulty: 2 Medium 54 Level of Difficulty: 3 Hard 14 Stevenson - Chapter 18 81 Topic: Characteristics of Waiting Lines 6 Topic: Constraint Management 6 Topic: Goal of Waiting-Line Management 10 Topic: Measures of Waiting-Line Performance 9 Topic: Operations Strategy 1 Topic: Queuing Model: Finite-Source 8 Topic: Queuing Models: Infinite-Source 33 Topic: The Psychology of Waiting 4 Topic: Why is There Waiting? 4 [Show More]

Last updated: 2 years ago

Preview 1 out of 21 pages