Clayton State University - BUSA 3101 Practice Test 2. With All Answers Chapter 4.

Document Content and Description Below

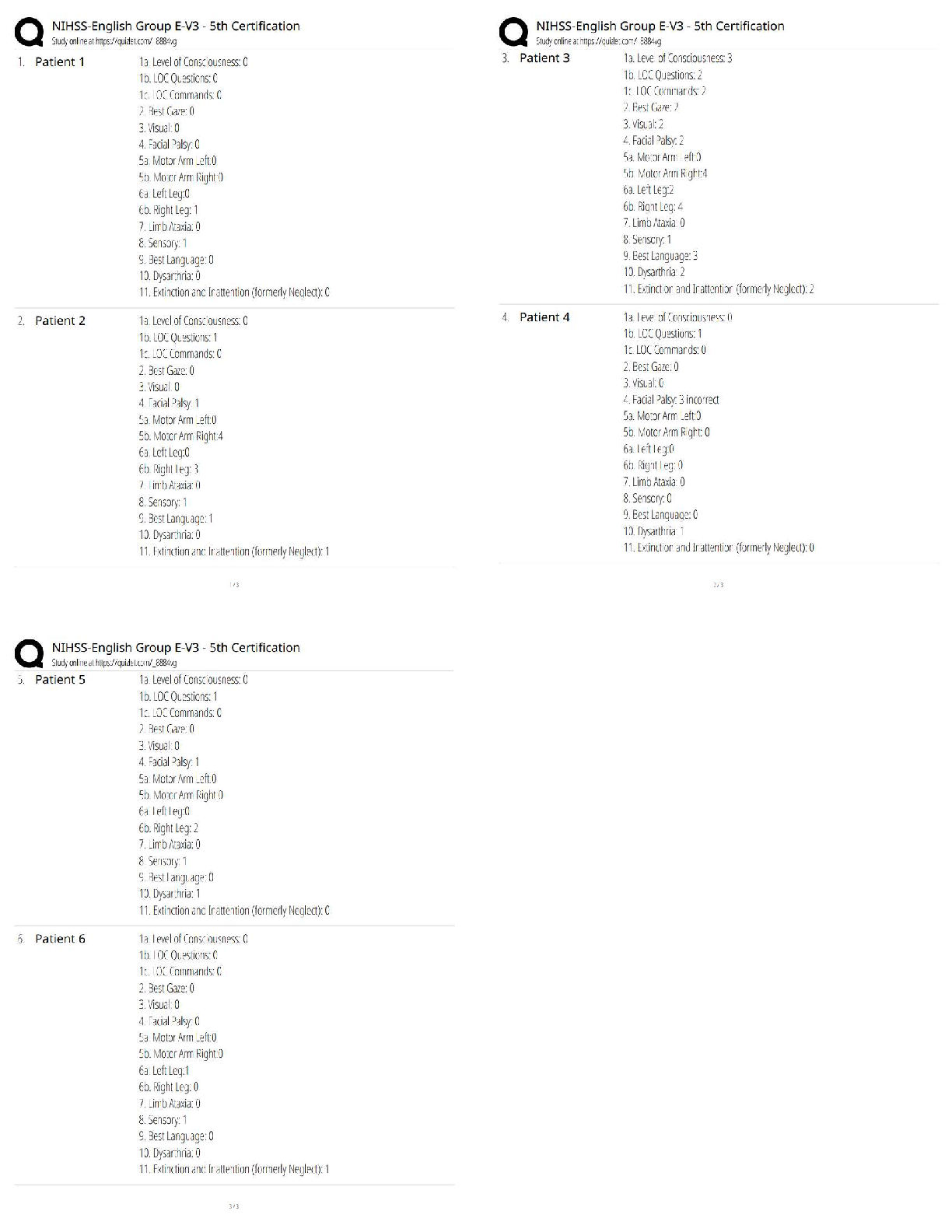
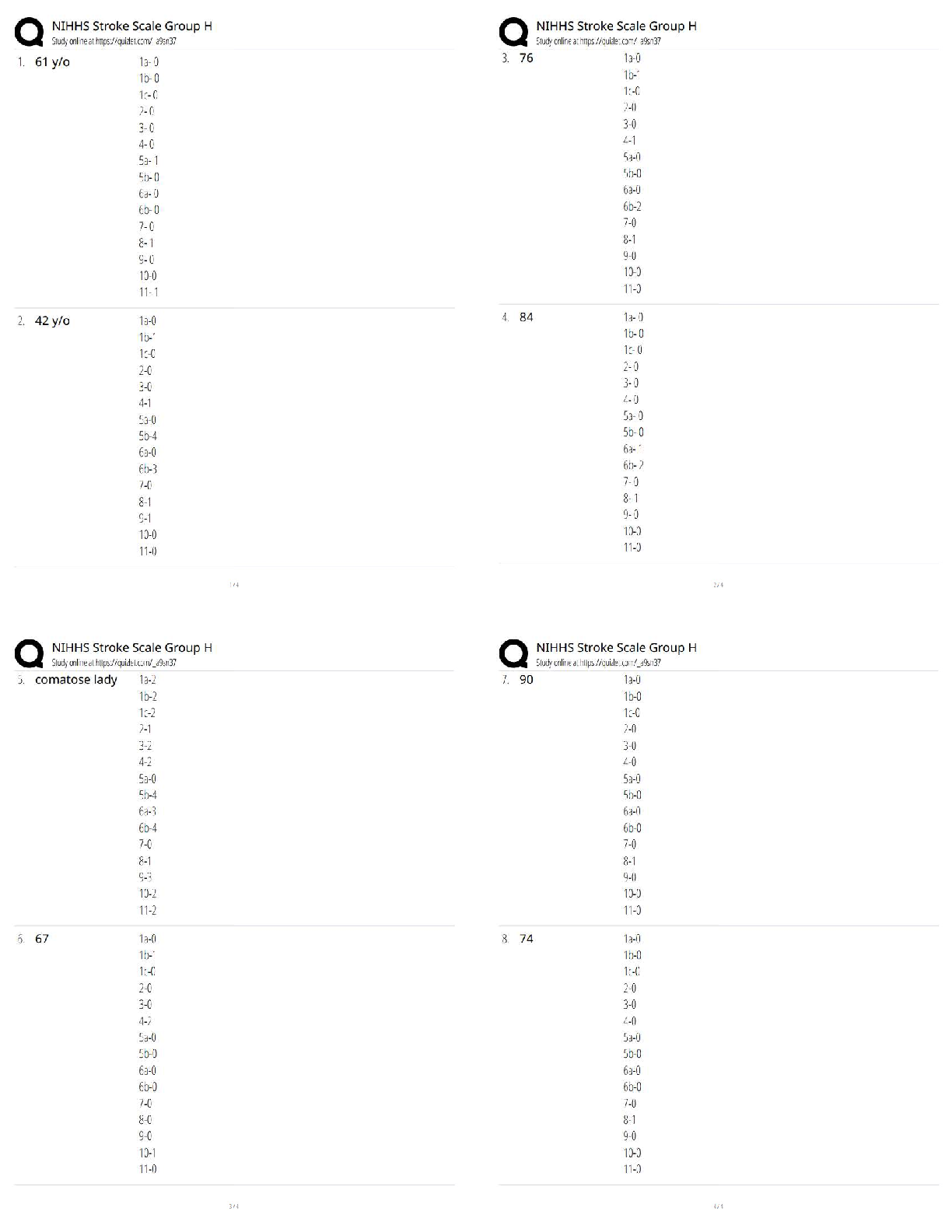
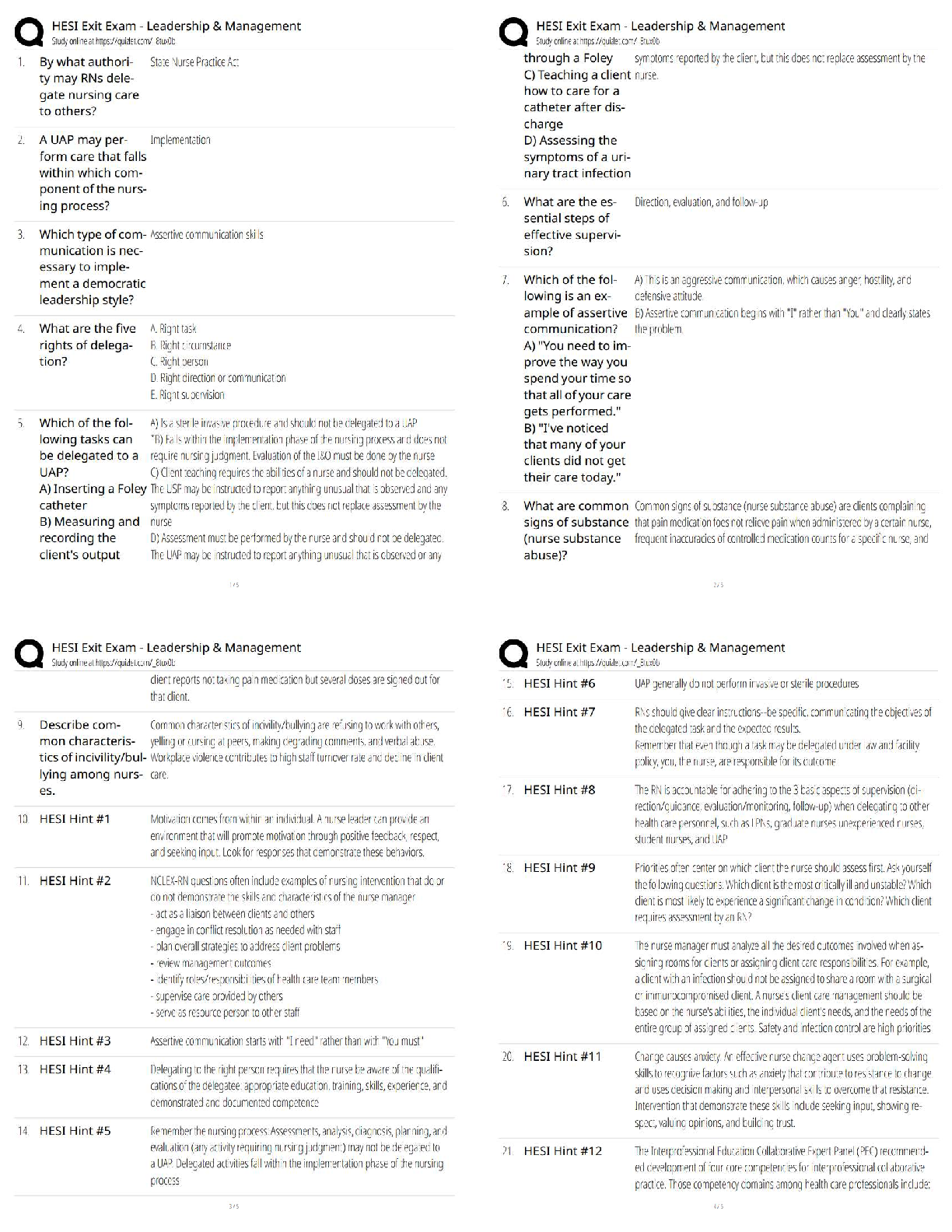
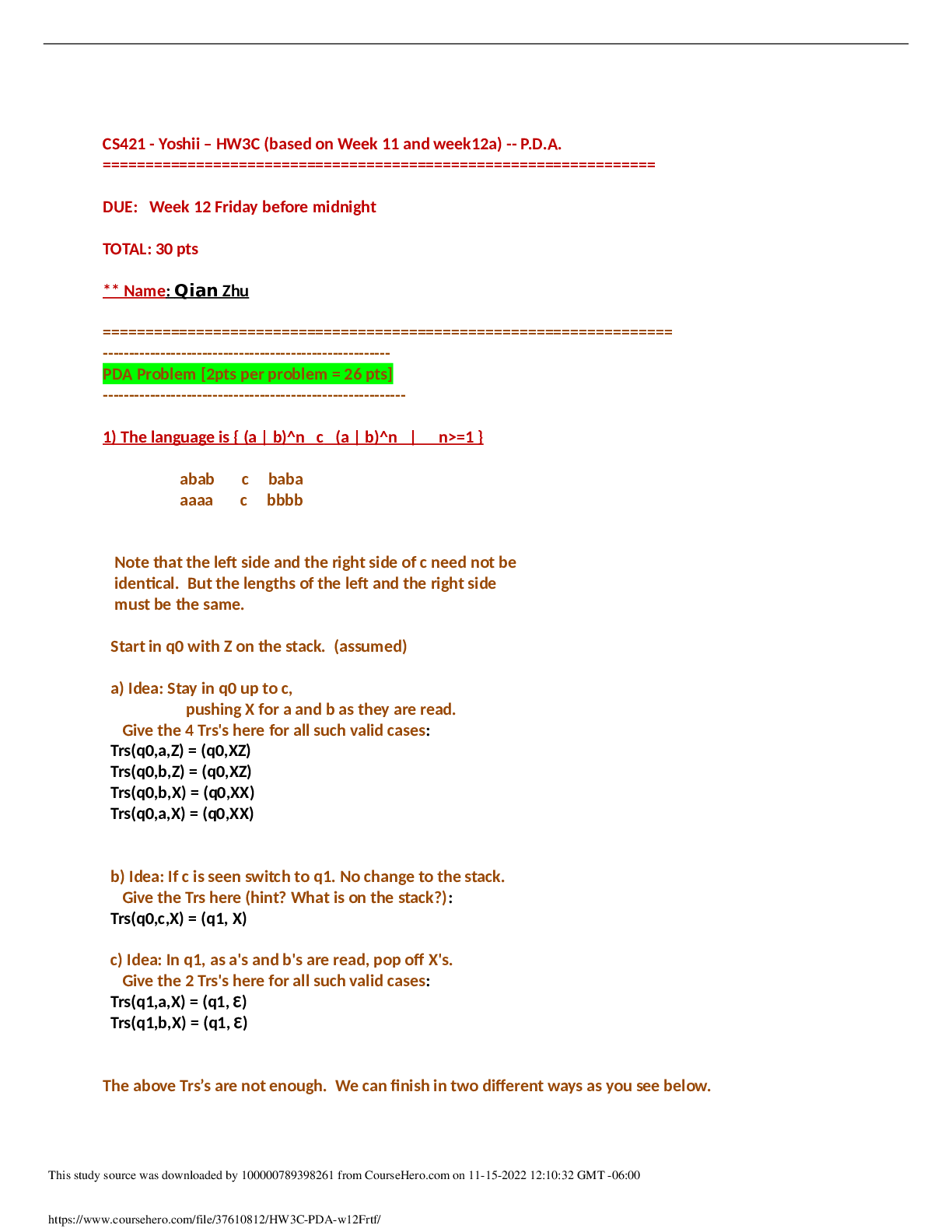
BUSA3101 Practice Test 2 With All Answers Chapter 4 9. A student scored in the 85th percentile on a standardized test. This means that the student scored lower than 85% of all students who took... the test. True False 10. The 50th percentile of a distribution is the same as the distribution mean. True False 15. Pearson's coefficient of skewness is a measure of a distribution's symmetry. True False 16. If a distribution is negatively skewed, the distribution is not symmetrical and the long tail is to the left. True False 24. A dot plot can be used to show _________________. A. The mean, median, and mode B. The general shape of a distribution for a nominal qualitative variable C. The distribution for a quantitative variable D. The interquartile range 28. In a distribution, the second quartile corresponds with the __________. A. Mean B. Median C. Mode D. Variance 30. To locate the percentile for a given observation in a data set, the data must be ___________. A. Sorted and listed from the minimum to the maximum values B. Displayed in a histogram C. Summarized in a frequency distribution D. Distributed symmetrically around the mean 32. In the following set of data: what are the first, second, and third quartiles? A. 1, 6, and 100 B. 3, 5, and 9 C. 3, 6, and 9 D. 1, 5, and 100 34. What statistics are needed to draw a box plot? A. The minimum, maximum, median, first and third quartiles. B. The median, mean, and standard deviation. C. The median and interquartile range. D. The mean and standard deviation. 40. If the coefficient of skewness is equal to zero, the shape of the distribution is __________. A. Negatively skewed B. Symmetric C. Positively skewed D. Unknown 42. The following graph is _______________. A. Positively skewed B. Negatively skewed C. Symmetric D. Uniformly distributed 43. A large oil company is studying the number of gallons of gasoline purchased per customer at self-service pumps. The mean number of gallons is 10.0, with a standard deviation of 3.0 gallons. The median is 10.75 gallons. What is Pearson's coefficient of skewness in this instance? A. -1.00 B. -0.75 C. +0.75 D. +1.00 48. The following graph illustrates _______________. A. A positive or direct relationship B. A negative or inverse relationship C. No relationship D. A distribution for a single variable 9. A student scored in the 85th percentile on a standardized test. This means that the student scored lower than 85% of all students who took the test. FALSE The 85% means that the student scored higher than 85% of all students. 10. The 50th percentile of a distribution is the same as the distribution mean. FALSE The 50th percentile is the same as the median. 15. Pearson's coefficient of skewness is a measure of a distribution's symmetry. TRUE 16. If a distribution is negatively skewed, the distribution is not symmetrical and the long tail is to the left. TRUE 24. A dot plot can be used to show _________________. A. The mean, median, and mode B. The general shape of a distribution for a nominal qualitative variable C. The distribution for a quantitative variable D. The interquartile range A dot plot "piles" or "stacks" observations on top of each other. This allows us to see the shape of the distribution. 28. In a distribution, the second quartile corresponds with the __________. A. Mean B. Median C. Mode D. Variance The second quartile is the value that separates the 50% of lower values from the 50% of the higher values, which corresponds to the median. 30. To locate the percentile for a given observation in a data set, the data must be ___________. A. Sorted and listed from the minimum to the maximum values B. Displayed in a histogram C. Summarized in a frequency distribution D. Distributed symmetrically around the mean Sorting or ranking the data is necessary to determine percentiles. 32. In the following set of data: what are the first, second, and third quartiles? A. 1, 6, and 100 B. 3, 5, and 9 C. 3, 6, and 9 D. 1, 5, and 100 The first quartile is located at position (7 + 1)(1/4) = 2, which corresponds with the data value, 3. The second quartile is located at position (7 + 1)(2/4) = 4, which correspond with the data value, 6. The third quartile is located at position (7 + 1)(3/4) = 6, which correspond with the data value, 9. 34. What statistics are needed to draw a box plot? A. The minimum, maximum, median, first and third quartiles. B. The median, mean, and standard deviation. C. The median and interquartile range. D. The mean and standard deviation. A box plot requires minimum, maximum, median, and the first and third quartile values. 40. If the coefficient of skewness is equal to zero, the shape of the distribution is __________. A. Negatively skewed B. Symmetric C. Positively skewed D. Unknown Based on Pearson's formula, the skewness is equal to zero when the mean and median are equal. 42. The following graph is _______________. A. Positively skewed B. Negatively skewed C. Symmetric D. Uniformly distributed The distribution is positively skewed because the distribution's long tail is to the right. 43. A large oil company is studying the number of gallons of gasoline purchased per customer at self-service pumps. The mean number of gallons is 10.0, with a standard deviation of 3.0 gallons. The median is 10.75 gallons. What is Pearson's coefficient of skewness in this instance? A. -1.00 B. -0.75 C. +0.75 D. +1.00 Pearson's coefficient of skewness is computed by 3(10.0 - 10.75)/3.0 = -0.75. 48. The following graph illustrates _______________. A. A positive or direct relationship B. A negative or inverse relationship C. No relationship D. A distribution for a single variable When two variables are positively related, an increase in the value of one variable corresponds with increases in the value of the other variable.   Chapter 5 1. The probability of rolling a 3 or 2 on a single die is an example of conditional probability. True False 2. The probability of rolling a 3 or 2 on a single die is an example of mutually exclusive events. True False 6. The joint probability of two independent events, A and B, is computed as P(A and B) = P(A) P(B). True False 7. The joint probability of two events, A and B, that are not independent is computed as P(A and B) = P(A) P(B|A). True False 8. A coin is tossed four times. The joint probability that all four tosses will result in a head is ¼ or 0.25. True False 9. If there are "m" ways of doing one thing, and "n" ways of doing another thing, the multiplication formula states that there are (m) × (n) ways of doing both. True False 14. The National Center for Health Statistics reported that of every 883 deaths in recent years, 24 resulted from an automobile accident, 182 from cancer, and 333 from heart disease. What is the probability that a particular death is due to an automobile accident? A. 24/883 or 0.027 B. 539/883 or 0.610 C. 24/333 or 0.072 D. 182/883 or 0.206 15. If two events A and B are mutually exclusive, what does the special rule of addition state? A. P(A or B) = P(A) + P(B) B. P(A and B) = P(A) + P(B) C. P(A and/or B) = P(A) + P(B) D. P(A or B) = P(A) - P(B) 16. What does the complement rule state? A. P(A) = P(A) - P(B) B. P(A) = 1 - P(not A) C. P(A) = P(A) × P(B) D. P(A) = P(A)X + P(B) 18. A study of 200 computer service firms revealed these incomes after taxes: What is the probability that a particular firm selected has $1 million or more in income after taxes? A. 0.00 B. 0.25 C. 0.49 D. 0.51 20. A survey of top executives revealed that 35% of them regularly read Time magazine, 20% read Newsweek, and 40% read U.S. News & World Report. A total of 10% read both Time and U.S. News & World Report. What is the probability that a particular top executive reads either Time or U.S. News & World Report regularly? A. 0.85 B. 0.06 C. 1.00 D. 0.65 22. A tire manufacturer advertises, "the median life of our new all-season radial tire is 50,000 miles. An immediate adjustment will be made on any tire that does not last 50,000 miles." You purchased four of these tires. What is the probability that all four tires will wear out before traveling 50,000 miles? A. 1/10 or 0.10 B. ¼ or 0.25 C. 1/64 or 0.0156 D. 1/16 or 0.0625 25. Giorgio offers the person who purchases an 8-ounce bottle of Allure two free gifts, either an umbrella, a 1-ounce bottle of Midnight, a feminine shaving kit, a raincoat, or a pair of rain boots. If you purchased Allure, what is the probability you randomly selected an umbrella and a shaving kit in that order? A. 0.00 B. 1.00 C. 0.05 D. 0.20 28. A gumball machine is filled with 50 black, 150 white, 100 red, and 100 yellow gumballs that have been thoroughly mixed. Sue and Jim each purchased one gumball. What is the likelihood both Sue and Jim get red gumballs? A. 0.50 B. 0.062 C. 0.33 D. 0.75 29. What does equal? A. 640 B. 36 C. 10 D. 120 31. In a management trainee program, 80% of the trainees are female, 20% male. A total of 90% of the females attended college, while 78% of the males attended college. A management trainee is selected at random. What is the probability that the person selected is a female who did attend college? A. 0.20 B. 0.08 C. 0.25 D. 0.72 36. An electronics firm sells four models of stereo receivers, three amplifiers, and six speaker brands. When the four types of components are sold together, they form a "system." How many different systems can the electronics firm offer? A. 36 B. 18 C. 72 D. 144 38. How many permutations of the three letters C, D, and E are possible? A. 3 B. 0 C. 6 D. 8 40. A developer of a new subdivision wants to build homes that are all different. There are three different interior plans that can be combined with any of five different home exteriors. How many different homes can be built? A. 8 B. 10 C. 15 D. 30 44. The first card selected from a standard 52-card deck was a king. [A deck has four sets (spades, hearts, diamonds, and clubs) each of which is “numbered” from 2 through 10 plus jack, queen, king, and ace.] If the first card is returned to the deck, what is the probability that a king will be drawn on the second selection? A. 1/4 or 0.25 B. 1/13 or 0.077 C. 12/13 or 0.923 D. 1/3 or 0.33 46. Which approach to probability assumes that the events are equally likely? A. Classical B. Empirical C. Subjective D. Mutually exclusive 70. An automatic machine inserts mixed vegetables into a plastic bag. Past experience revealed that some packages were underweight and some were overweight, but most of them had satisfactory weight. What is the probability of selecting three packages that are overweight? A. 0.0000156 B. 0.0004219 C. 0.0000001 D. 0.075 1. The probability of rolling a 3 or 2 on a single die is an example of conditional probability. FALSE This is classical probability. 2. The probability of rolling a 3 or 2 on a single die is an example of mutually exclusive events. TRUE 6. The joint probability of two independent events, A and B, is computed as P(A and B) = P(A) P(B). TRUE AACSB: Communication Blooms: Remember Difficulty: 2 Medium Learning Objective: 05-05 Calculate probabilities using the rules of multiplication. Topic: Rules of Multiplication 7. The joint probability of two events, A and B, that are not independent is computed as P(A and B) = P(A) P(B|A). TRUE AACSB: Communication Blooms: Remember Difficulty: 2 Medium Learning Objective: 05-04 Define the term joint probability. Topic: Rules of Multiplication 8. A coin is tossed four times. The joint probability that all four tosses will result in a head is ¼ or 0.25. FALSE Each outcome's probability is .5. The joint probability is (.5)(.5)(.5)(.5) = 0.0625. AACSB: Analytic Blooms: Apply Difficulty: 2 Medium Learning Objective: 05-05 Calculate probabilities using the rules of multiplication. Topic: Rules of Multiplication 9. If there are "m" ways of doing one thing, and "n" ways of doing another thing, the multiplication formula states that there are (m) × (n) ways of doing both. TRUE 14. The National Center for Health Statistics reported that of every 883 deaths in recent years, 24 resulted from an automobile accident, 182 from cancer, and 333 from heart disease. What is the probability that a particular death is due to an automobile accident? A. 24/883 or 0.027 B. 539/883 or 0.610 C. 24/333 or 0.072 D. 182/883 or 0.206 Based on the empirical approach to probability, 24/883 = 0.027. AACSB: Analytic Blooms: Apply Difficulty: 2 Medium Learning Objective: 05-02 Identify and apply the appropriate approach to assigning probabilities. Topic: Approaches to Assigning Probabilities 15. If two events A and B are mutually exclusive, what does the special rule of addition state? A. P(A or B) = P(A) + P(B) B. P(A and B) = P(A) + P(B) C. P(A and/or B) = P(A) + P(B) D. P(A or B) = P(A) - P(B) By definition. P(A or B) = P(A) + P(B) is the special rule of addition. AACSB: Communication Blooms: Remember Difficulty: 2 Medium Learning Objective: 05-03 Calculate probabilities using the rules of addition. Topic: Rules of Addition 16. What does the complement rule state? A. P(A) = P(A) - P(B) B. P(A) = 1 - P(not A) C. P(A) = P(A) × P(B) D. P(A) = P(A)X + P(B) By definition, P(A) plus its complement, P(not A) must equal 1. 18. A study of 200 computer service firms revealed these incomes after taxes: What is the probability that a particular firm selected has $1 million or more in income after taxes? A. 0.00 B. 0.25 C. 0.49 D. 0.51 A couple of approaches can be used to answer the question. Using the complement rule, the probability of firms less than $1 million is 102/200 = 0.51. The complement or firms with $1 million or more income is 1.0 - 0.51 = 0.49. 20. A survey of top executives revealed that 35% of them regularly read Time magazine, 20% read Newsweek, and 40% read U.S. News & World Report. A total of 10% read both Time and U.S. News & World Report. What is the probability that a particular top executive reads either Time or U.S. News & World Report regularly? A. 0.85 B. 0.06 C. 1.00 D. 0.65 The three events—reading Time, Newsweek, or U.S. News—are not mutually exclusive because executives can read more than one of the magazines. The P(Time or U.S. News) = P(Time) + P(U.S. News) - P(Time and U.S. News) = 0.35 + 0.40 - 0.10 = 0.65. 22. A tire manufacturer advertises, "the median life of our new all-season radial tire is 50,000 miles. An immediate adjustment will be made on any tire that does not last 50,000 miles." You purchased four of these tires. What is the probability that all four tires will wear out before traveling 50,000 miles? A. 1/10 or 0.10 B. ¼ or 0.25 C. 1/64 or 0.0156 D. 1/16 or 0.0625 The median corresponds with the 50th percentile. So the probability that a tire wears out before 50,000 miles is 0.5. Each outcome's probability is .5. The joint probability is (.5)(.5)(.5)(.5) = 0.0625. 25. Giorgio offers the person who purchases an 8-ounce bottle of Allure two free gifts, either an umbrella, a 1-ounce bottle of Midnight, a feminine shaving kit, a raincoat, or a pair of rain boots. If you purchased Allure, what is the probability you randomly selected an umbrella and a shaving kit in that order? A. 0.00 B. 1.00 C. 0.05 D. 0.20 There are five different gifts. Therefore, the probability of any gift is 1/5 = .2. The probability of selecting a second gift is a conditional probability that assumes the first selection was an umbrella, so the probability of a second gift, a shaving kit, is ¼ = 0.25. The joint probability is (1/5)(1/4) = 1/20 = 0.05. 28. A gumball machine is filled with 50 black, 150 white, 100 red, and 100 yellow gumballs that have been thoroughly mixed. Sue and Jim each purchased one gumball. What is the likelihood both Sue and Jim get red gumballs? A. 0.50 B. 0.062 C. 0.33 D. 0.75 The probability of a red gumball on the first selection is 100/400 = .25. The probability of selecting a second red gumball is a conditional probability that assumes the first selection was a red gumball, so the probability of a second red gumball is 99/399. The Joint probability is (100/400)(99/399) = 0.062. 29. What does equal? A. 640 B. 36 C. 10 D. 120 (6*5*4*3*2*1)(2*1)/(4*3*2*1)(3*2*1) = 10 36. An electronics firm sells four models of stereo receivers, three amplifiers, and six speaker brands. When the four types of components are sold together, they form a "system." How many different systems can the electronics firm offer? A. 36 B. 18 C. 72 D. 144 Using the multiplication formula, (4)(3)(6) = 72. 38. How many permutations of the three letters C, D, and E are possible? A. 3 B. 0 C. 6 D. 8 Using the permutation formula 3!/0! = (3)(2)(1) = 6. 40. A developer of a new subdivision wants to build homes that are all different. There are three different interior plans that can be combined with any of five different home exteriors. How many different homes can be built? A. 8 B. 10 C. 15 D. 30 Using the multiplication formula, (3)(5) = 15. 44. The first card selected from a standard 52-card deck was a king. If it is returned to the deck, what is the probability that a king will be drawn on the second selection? A. 1/4 or 0.25 B. 1/13 or 0.077 C. 12/13 or 0.923 D. 1/3 or 0.33 The probability is 4/52 = 1/13, or 0.077. 46. Which approach to probability assumes that the events are equally likely? A. Classical B. Empirical C. Subjective D. Mutually exclusive By definition, the classical approach assumes that events are equally likely. 70. An automatic machine inserts mixed vegetables into a plastic bag. Past experience revealed that some packages were underweight and some were overweight, but most of them had satisfactory weight. What is the probability of selecting three packages that are overweight? A. 0.0000156 B. 0.0004219 C. 0.0000001 D. 0.075 Apply the multiplication rule: (0.075)(0.075)(0.075) = 0.0004219.   Chapter 6 2. The probability of a particular outcome must always be between 0.0 and 1.0 inclusive. True False 5. To construct a binomial probability distribution, the mean must be known. True False 6. To construct a binomial distribution, it is necessary to know the total number of trials and the probability of success on each trial. True False 7. The mean of a probability distribution is called its expected value. True False 14. If the variance is 3.6 grams, what is the standard deviation? A. 0.600 B. 1.897 C. 6.000 D. 12.96 15. A total of 60% of the customers of a fast food chain order a hamburger, French fries, and a drink. If a random sample of 15 cash register receipts is selected, what is the probability that 10 or more will show that the above three food items were ordered? A. 1.000 B. 0.186 C. 0.403 D. 0.000 19. Sweetwater & Associates write weekend trip insurance at a very nominal charge. Records show that the probability that a motorist will have an accident during the weekend and file a claim is 0.0005. Suppose they wrote 400 policies for the coming weekend, what is the probability that exactly two claims will be filed? A. 0.8187 B. 0.2500 C. 0.0164 D. 0.0001 21. Which one of the following is NOT a condition of the binomial distribution? A. Independent trials B. Only two outcomes C. The probability of success remains constant from trial to trial D. Sampling at least 10 trials 28. Carlson Jewelers permits the return of their diamond wedding rings, provided the return occurs within two weeks of the purchase date. Their records reveal that 10% of the diamond wedding rings are returned. Five different customers buy a wedding ring. What is the probability that none of the customers return a ring? A. 0.250 B. 0.073 C. 0.590 D. 0.500 33. A manufacturer of headache medicine claims it is 70% effective within a few minutes. That is, out of every 100 users, 70 get relief within a few minutes. A group of 12 patients are given the medicine. If the claim is true, what is the probability that eight have relief within a few minutes? A. 0.001 B. 0.168 C. 0.667 D. 0.231 34. A true/false test consists of six questions. If you guess the answer to each question, what is the probability of getting all six questions correct (rounded to four decimal places)? A. 0 B. 0.016 C. 0.062 D. 0.250 36. A tennis match requires that a player win three of five sets to win the match. If a player wins the first two sets, what is the probability that the player wins the match, assuming that each player is equally likely to win each set? A. 0.500 B. 0.125 C. 0.875 D. 0.000 38. A coin is tossed four times. The following table summarizes the experiment. What is the following table called? A. Probability distribution B. Cumulative frequency distribution C. Standard deviation D. Frequency table 41. What must you know to develop a binomial probability distribution? A. The probability of success B. The probability of success and the number of trials C. The probability of success and the number of successes D. The number of trials and the number of successes 45. David's gasoline station offers 4 cents off per gallon if the customer pays in cash and does not use a credit card. Past evidence indicates that 40% of all customers pay in cash. During a one-hour period, 15 customers buy gasoline at this station. What is the probability that all 15 pay in cash (rounded to one decimal place)? A. 0.0 B. 0.1 C. 0.9 D. 1.0 51. A company is studying the number of monthly absences among its 125 employees. The following probability distribution shows the likelihood that people were absent 0, 1, 2, 3, 4, or 5 days last month. What is the mean number of days absent? A. 1.00 B. 0.40 C. 0.72 D. 2.5 55. A company is studying the number of monthly absences among its 125 employees. The following probability distribution shows the likelihood that people were absent 0, 1, 2, 3, 4, or 5 days last month. What is the standard deviation of the number of days absent? A. 1.1616 B. 0 C. 1.6595 D. 1.0778 62. The following is a binomial probability distribution with n = 3 and π = 0.20. The mean of the distribution is _______. A. 1.50 B. 0.60 C. 0.25 D. 0.00 2. The probability of a particular outcome must always be between 0.0 and 1.0 inclusive. TRUE 5. To construct a binomial probability distribution, the mean must be known. FALSE To construct a binomial probability distribution, the number of trials and the probability of a success must be known. AACSB: Communication Blooms: Remember Difficulty: 1 Easy Learning Objective: 06-05 Describe and compute probabilities for a binomial distribution. Topic: Binomial Probability Distribution 6. To construct a binomial distribution, it is necessary to know the total number of trials and the probability of success on each trial. TRUE AACSB: Communication Blooms: Remember Difficulty: 1 Easy Learning Objective: 06-05 Describe and compute probabilities for a binomial distribution. Topic: Binomial Probability Distribution 7. The mean of a probability distribution is called its expected value. TRUE 14. If the variance is 3.6 grams, what is the standard deviation? A. 0.600 B. 1.897 C. 6.000 D. 12.96 The standard deviation is the square root of the variance; the square root of 3.6 is 1.897. AACSB: Analytic Blooms: Understand Difficulty: 1 Easy Learning Objective: 06-04 Compute the variance and standard deviation of a probability distribution. Topic: The Variance and Standard Deviation of a Probability Distribution 15. A total of 60% of the customers of a fast food chain order a hamburger, French fries, and a drink. If a random sample of 15 cash register receipts is selected, what is the probability that 10 or more will show that the above three food items were ordered? A. 1.000 B. 0.186 C. 0.403 D. 0.000 Applying the binomial distribution, go to the binomial probability table, find the case where the number of trials is n = 15, and the probability of success is π = .60. Find the row where x, the number of successes, is 10. Finally, add the probabilities for 10 through 15 successes (.186 + .127 + … + .005 + .000). The result is .403. 19. Sweetwater & Associates write weekend trip insurance at a very nominal charge. Records show that the probability that a motorist will have an accident during the weekend and file a claim is 0.0005. Suppose they wrote 400 policies for the coming weekend, what is the probability that exactly two claims will be filed? A. 0.8187 B. 0.2500 C. 0.0164 D. 0.0001 In this case, we use the Poisson distribution by first computing the mean, µ = 400*.0005 = 0.20. Then, go to the Poisson probability distribution table. Find the column where µ = 0.2, go down the left column to the row where x = 2. The value at the intersection is .0164. 21. Which one of the following is NOT a condition of the binomial distribution? A. Independent trials B. Only two outcomes C. The probability of success remains constant from trial to trial D. Sampling at least 10 trials All are conditions for a binomial distribution except that there is no requirement regarding the number of trials. 28. Carlson Jewelers permits the return of their diamond wedding rings, provided the return occurs within two weeks of the purchase date. Their records reveal that 10% of the diamond wedding rings are returned. Five different customers buy a wedding ring. What is the probability that none of the customers return a ring? A. 0.250 B. 0.073 C. 0.590 D. 0.500 Applying the binominal probability distribution, go to the binomial probability table, find the case where the number of trials is n = 5, and the probability of success is π = .10. Find the row where x, the number of successes, is 0. The result is .590. 33. A manufacturer of headache medicine claims it is 70% effective within a few minutes. That is, out of every 100 users, 70 get relief within a few minutes. A group of 12 patients are given the medicine. If the claim is true, what is the probability that eight have relief within a few minutes? A. 0.001 B. 0.168 C. 0.667 D. 0.231 Applying the Binomial Distribution, go to the binomial probability table, find the case where the number of trials is n = 12, and the probability of success is π = .70. Find the row where x, the number of successes, is 8. The probability that 8 of 12 people have relief is .231. 34. A true/false test consists of six questions. If you guess the answer to each question, what is the probability of getting all six questions correct? A. 0 B. 0.016 C. 0.062 D. 0.250 Applying the Binomial Distribution, go to the binomial probability table, find the case where the number of trials is n = 6 and the probability of success is π = .50. Find the row where x, the number of successes, is 6. The probability of getting all six correct is 0.016. 36. A tennis match requires that a player win three of five sets to win the match. If a player wins the first two sets, what is the probability that the player wins the match, assuming that each player is equally likely to win each set? A. 0.500 B. 0.125 C. 0.875 D. 0.000 There are 3 ways the winner of the first two sets can win another set and win the match: The player can (1) win the third set, (2) lose the third set and win the fourth set, and (3) lose sets three and four and win the fifth set. The probabilities for these three events are: Win the third set: P(W3) = .50 Lose the third set and win the fourth set: P(W4) = P(L3)P(W4) = .50(.50) = .250 Lose the third and fourth sets and win the fifth set: P(W5) = P(L3)P(L4)P(W5) = .50(.50)(.50) = .125 Applying the special rule of addition, the sum of these three probabilities is .875. 38. A coin is tossed four times. The following table summarizes the experiment. What is the following table called? A. Probability distribution B. Cumulative frequency distribution C. Standard deviation D. Frequency table This is a probability distribution. The outcomes are collectively exhaustive and mutually exclusive; the probabilities of the outcomes are between 0 and 1, and sum to 1. 41. What must you know to develop a binomial probability distribution? A. The probability of success B. The probability of success and the number of trials C. The probability of success and the number of successes D. The number of trials and the number of successes By definition, a particular binomial distribution is specified by n, the number of trials, and π, the probability of a successful trial. 45. David's gasoline station offers 4 cents off per gallon if the customer pays in cash and does not use a credit card. Past evidence indicates that 40% of all customers pay in cash. During a one-hour period, 15 customers buy gasoline at this station. What is the probability that all 15 pay in cash? A. 0.0 B. 0.1 C. 0.9 D. 1.0 Applying the binomial distribution, go to the binomial probability table, find the case where the number of trials is n = 15 and the probability of success is π = .40. Find the row where x, the number of successes, is 15. Find the corresponding probability of 0.000. [Or use the multiplication approach, multiplying .4 fifteen times or 0.4^15]. 51. A company is studying the number of monthly absences among its 125 employees. The following probability distribution shows the likelihood that people were absent 0, 1, 2, 3, 4, or 5 days last month. What is the mean number of days absent? A. 1.00 B. 0.40 C. 0.72 D. 2.5 To find the mean: µ = 0(.60) + 1(.20) + 2(.12) + 3(.04) + 4(.04) = 0.72. So the average number of days absent is 0.72 days per employee per month. 55. A company is studying the number of monthly absences among its 125 employees. The following probability distribution shows the likelihood that people were absent 0, 1, 2, 3, 4, or 5 days last month. What is the standard deviation of the number of days absent? A. 1.1616 B. 0 C. 1.6595 D. 1.0778 To find the variance: σ2 = (0 - .72)2(.60) + (1 - .72)2(.20) + (2 -.72)2(.12) + (3 - .72)2(.04) + (4 - .72)2(.04) = 1.1616. The standard deviation is the square root of the variance, or the square root of 1.1616, which is 1.0778. 62. The following is a binomial probability distribution with n = 3 and π = 0.20. The mean of the distribution is _______. A. 1.50 B. 0.60 C. 0.25 D. 0.00 The mean of a binomial distribution is found by nπ = 3(.20) = .60. [Show More]

Last updated: 2 years ago

Preview 1 out of 56 pages